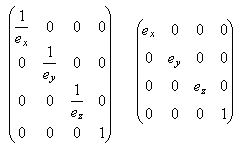Tutorial Kollision3

Kollisionsbehandlung in Programmen

Zu diesem Tutorial

Mit diesem dritten Teil des Kollisions-Tutorials schließe ich die Serie ab. Nach den ersten beiden Teilen sind sicherlich noch Fragen offen geblieben, wovon in einige aufgreifen möchte. Es geht vor allem um Ergänzungen zum Verfahren, das ich im 2. Teil vorgestellt habe. Mit dem nackten Algorithmus ist es ja nicht getan; er muss irgendwie in das Programm eingebunden werden. Doch hierbei gehen die Wege auseinander, denn es gibt einfach zu viele verschiedene Ansätze und Programmkonzeptionen, so dass ich mich im folgenden auf Hinweise und Tipps beschränken muss. Ich hoffe aber, dass trotzdem die eine oder andere Anregung erhaltet.

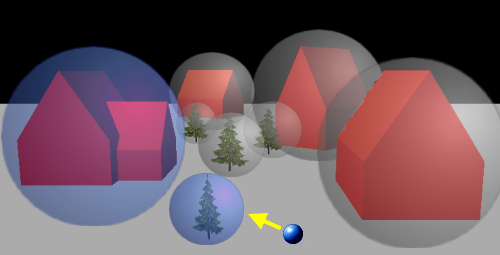
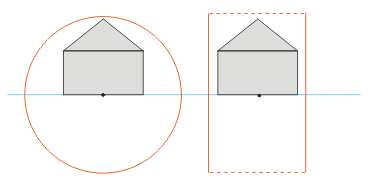
Gelegentlich werde ich mich auf die Beiträge von Nettle, Kauerby und Rouwe beziehen, die ich im 2. Teil vorgestellt habe. Dort befinden sich auch die Links. Schließlich sollte ich noch die Testumgebung, mit der ich die Kollisionen untersucht habe, wenigstens im Bild vorstellen:

Die Testumgebung.

Einfache Häuser, die mit ihren Ecken, Kanten und verschieden ausgerichteten Polygonen ideal für den Zweck sind. Die Kollision an den Bäumen erfolgt in besonderer Weise, darauf gehe ich aber nicht näher ein.

Von der Kugel zum Ellipsoid

Naheliegend - aber nicht besonders gut

Als erstes möchte ich die Erweiterung zum Ellipsoid aufgreifen. Es leuchtet ein, dass ein Objekt in manchen Fällen besser durch ein Ellipsoid dargestellt werden kann als durch eine Kugel. Ich will aber gleich vorausschicken, dass wir nicht allzuviel davon erwarten sollten. Das wird im folgenden noch deutlich werden, denke ich. Außerdem möchte ich hier nicht näher auf die mathematischen Grundlagen des Ellipsoids eingehen; Informationen dazu gibt es reichlich.

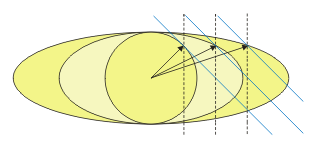
Eigentlich liegt die Vorgehensweise auf der Hand. Die Kugel ist ein Sonderfall des Ellipsoids, und infolgedessen bietet sich an, in den betroffenen Funktionen die Kugel durch das allgemeinere Ellipsoid zu ersetzen. Paul Nettle schlägt diesen Weg vor; in dem Kapitel "Making It Ellipsoidal" in seinem Beitrag beschreibt er, wie es gemacht wird. Nach seinem Vorschlag scheint es ziemlich einfach zu sein, entsprechend der Spreizung des Ellipsoids wird die Normale der Kollisionsebene ebenfalls gespreizt und invertiert auf den Mittelpunkt des Ellipsoids gesetzt. Das Ergebnis ist der gesuchte Intersektionspunkt auf der Oberfläche des Ellipsoids, also der Punkt, der im Kollisionsfall die Polygonebene berühren soll. Wenn wir aber genauer hinschauen, ist das nur annähernd der Erstberührungspunkt. Die Tangente in diesem Punkt liegt nämlich nicht genau parallel zur Kollisionsebene, wobei der Fehler umso größer ist, je länglicher das Ellipsoid ist. Die folgende Zeichnung zeigt das Problem.

Verschiedene Ellipsoide treffen in einem Winkel von 45° auf eine Ebene (blaue Linie).

Nun könnten wir einwenden, dass diese Ungenauigkeit vernachlässigbar ist, und tatsächlich fällt es kaum auf, wenn das Ellipsoid ein wenig in die Ebene einschneidet. Das eigentliche Problem ist die Kollision an den Polygonkanten. Ich erwähnte bereits im 2. Teil, dass Nettle dafür ein Näherungsverfahren vorschlägt. Der Intersektionspunkt wird durch Projektion des Ebenen-Intersektionspunktes auf die Kante bestimmt. Das kann, wenn die Kante schräg angeschnitten wird, schon bei der Kugel zu Kollisionslücken führen. Beim Ellipsoid tritt der Negativeffekt noch verstärkt auf.

Ein genaueres Verfahren ...

Und was ist mit dem von mir vorgestellten Algorithmus, der auf ähnlichen Grundgedanken basiert wie die Vorschläge von K. Fauerby und J. Rouwe? Die Berechnung mit der Kugel ist genau, lässt sich aber nicht ohne weiteres auf das Ellipsoid übertragen. Zumindest kenne ich keinen Weg, die exakten Berechnungen mit dem Ellipsoid durchzuführen, und wenn es tatsächlich möglich sein sollte, dürfte das alles extrem kompliziert und aufwendig sein. So schlagen Fauerby und Rouwe denn auch einen Weg vor, der auf den ersten Blick verblüfft: Wenn es schon nicht gelingt, die Kugel zu einem Ellipsoid zu spreizen, dann quetschen wir einfach die Welt so zusammen, dass sie zur Kugel passt. Kauerby hat, um das Verfahren zu begründen, eine recht anschauliche Nachhilfestunde zum Thema Vektorraum gegeben, doch ich denke, ein Bild zeigt die Zusammenhänge ebenso deutlich wie eine mathematische Beweisführung. Wer dem Braten nicht traut, kann sich ja mal mit dem Kapitel in Kauerbys Beitrag auseinandersetzen.

Links die Suituation: Das Ellipsoid bewegt sich in einem Winkel von 45° auf eine Ebene zu. Im zweiten Bild ist die Welt zusammengestaucht, so dass wir mit einer Kugel operieren können. Diese kollidiert mit der Ebene (3. Bild), wobei sich der Intersektionspunkt exakt berechnen lässt. Das 4. Bild zeigt, dass sich dieser Punkt sauber auf das Ellipsoid übertragen lässt. Das letzte Bild demonstriert noch einmal, wie die Kollision nach P. Nettle aussehen würde.

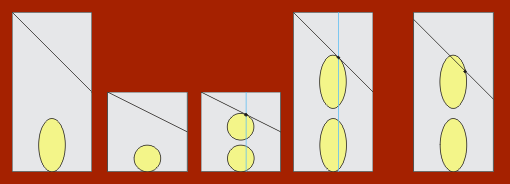
Zugegeben, als mir erstmals durch den Kopf ging, dass wir dazu jedes in Frage kommende Polygon auf die Verhältnisse des Ellipsoids umrechnen müssen, erschrak ich ein wenig. Doch beim genauen Hinschauen ist der Aufwand gar nicht so erheblich. In Anbetracht dessen, was wir zur Kollisionsberechnung ohnehin mit jedem Polygon anstellen müssen, fällt die zusätzliche Rechnung kaum ins Gewicht. Die Nadel am Fps-Tacho lässt jedenfalls keinen sichtbaren Ausschlag erkennen.

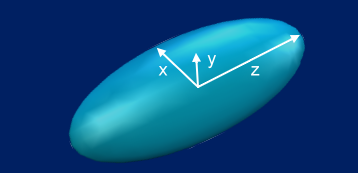
Wie wird die Welt denn nun umgerechnet? Wir gehen vom Ellipsoid aus und beschreiben dessen Form mit Hilfe eines Vektors. Die Komponenten des Vektors sind die drei Radien. Der Formvektor einer Kugel wäre demnach (1.0 1.0 1.0).

Ein Ellipsoid mit eingezeichnetem Radienvektor.

Aus den Komponenten dieses Vektors leiten wir nun die Skalierungsmatrix ab, mit der wir die Polygone bearbeiten. Klar, dass wir vor der Kollisionsberechnung die inverse Matrix ansetzen müssen, denn je länglicher das Ellipsoid ist, desto stärker muss die Welt gestaucht werden. Dass alles geschieht selbstverständlich nur temporär; die originalen Koordinaten bleiben erhalten. Ebenso müssen wir die Position und den Bewegungsvektor durch die inverse Matrix schieben, denn wie gesagt, alles muss auf das Ellipsoid zugeschnitten sein. Nach erfolgter Kollisionsberechnung werden Position und Bewegung, die durch die Kollision verstellt wurden, mit der nicht invertierten Matrix zurückgerechnet. Wie man im Bild sieht, sind die Matrizen denkbar einfach aufgebaut:

Die inverse(links) und normale Matrix für die kurzzeitige Koordinatentransformation.

Im Grunde brauchen wir für die Umrechnungen gar keine Matrizen, sie sollen hier nur den Zusammenhang deutlich machen. In Wirklichkeit werden wir die Vektoren einfach komponentenweise multiplizieren oder dividieren. Die Stellen, wo die Umrechnung erfolgen kann, habe ich bereits im Code (2. Teil des Tutorials) gekennzeichnet.

... mit begrenzten Möglichkeiten

So, und nun kommt noch ein Wermutstropfen. Das Verfahren funktioniert nur einwandfrei und genau, wenn das Ellipsoid an den Achsen des Welt-Koordinatensystems ausgerichtet ist; es darf nicht rotiert werden. Genau das würde die Sache aber erst richtig attraktiv machen. Stellen wir uns vor, das Ellipsoid sollte eine Maus verkörpern. Gut, das Schwänzchen ignorieren wir mal, es wird wohl kaum eine wirksame Kollision auslösen. Aber die Schnauze immer im Z-Richtung? Auch wenn die Maus mal nach Osten, also in X-Richtung flitzen will?

Kauerby geht m.W. auf diese Einschränkung nicht ein, und Rouwe erwähnt sie nur am Rande. Als ich den Hinweis fand, hatte ich bereits etliche Stunden vergeblich damit verbracht, eine geeinete Rotations-Skalierungs-Matrix zu finden, denn dass die Welt entsprechend der Ausrichtung des Ellipsoids skaliert und rotiert werden muss, liegt auf der Hand. Doch die kombinierte Matrix hat ihre Tücken. An den meisten Polygonen scheint die Kollision vernünftig zu arbeiten, aber dann gibt es einige Polygone, in deren Ebene das Ellipsoid eintaucht oder von dem es Abstand hält, je nachdem, wie das Polygon ausgerichtet ist. Baut man die Matrix anders auf, sind die Berührungen zwar einwandfrei, doch die Berechnung der Gleitebene funktioniert nicht mehr, weil die Relationen der Winkel zueinander nicht mehr stimmen. Beispiel:

Beispiel für falsche Gleitebene.

Fazit: Wenn wir uns damit begnügen, dass das Ellipsoid starr an den Hauptachsen ausgerichtet ist und bleibt, können wir eine sehr exakte Kollisionsberechnung vornehmen. Es gibt bestimmt Fälle, wo das möglich ist. Wünschen wir aber eine orientierte Fortbewegung (orientiert im dem Sinne, dass das Objekt entsprechend der Bewegungsrichtung ausgerichtet wird), dann greifen wir besser zur Kugel und nehmen gewisse Ungenauigkeiten in Kauf. Bei sehr lang gestreckten Objekten können wir evtl. mehrere Kugeln nehmen. Oft reichen zwei, eine für den Kopf, die zweite für das Hinterteil. Die Kollisionserkennung führen wir mit beiden Kugeln durch. Das hat außerdem den Vorteil, dass wir erkennen, womit das Objekt anstößt, und wir können die neue Körperausrichtung und Bewegungsrichtung wesentlich detaillierter bestimmen.

Daten vorbereiten

Wollen wir eine Szenerie nicht nur zeichnen, sondern darüber hinaus "kollisionsfähig" machen, müssen wir wahrscheinlich etwas umdenken und uns von gewohnten Abläufen trennen. Ohne Kollision nämlich transportieren wir normalerweise die Objekte mit glTranslate an die vorgesehene Stelle, bringen sie mit glRotate in die richtige Lage und mit glScale in die gewünschte Form. Das alles besorgt OpenGL mit seiner Modelview-Matrix, um die Umrechnung der Koordinaten kümmern wir uns nicht großartig.

Anders, wenn die Kollision hinzukommt. Nun benötigen wir selber die verschobenen, rotierten und skalierten Polygonkoordinaten, um die Kollisionen richtig berechnen zu können. Am besten schauen wir uns dazu die Bearbeitungskette an. Ich gehe davon aus, dass wir alle Optionen bezüglich der Rotation oder Skalierung ausnutzen wollen. Wir haben also eine Reihe verschiedener Objekte wie Bäume oder Gebäude, die jeweils mehrfach in die Szenerie gesetzt werden, mit unterschiedlichen Ausrichtungen (Rotation um drei Achsen) und Skalierungen (beliebig in den drei Dimensionen). Gerade die Skalierung in Verbindung mit verschiedenen Texturen erlaubt es, aus demselben Grundobjekt mehrere Erscheinungsformen zu zaubern.

Modellbeschreibung

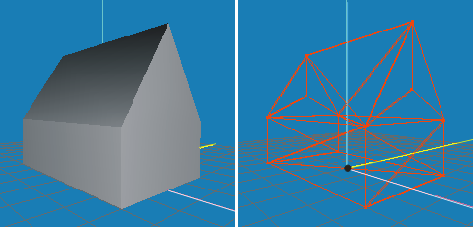
Am Anfang der Bearbeitungskette steht wahrscheinlich ein 3D-Programm wie Blender oder 3ds-Max, dessen Output wir in irgendeiner Form in unser Programm einlesen, entweder direkt mit Hilfe eines Model-Loaders oder über den Umweg einer Modelldatei, die wir unseren persönlichen Bedürfnissen angepasst haben. Ich bevorzuge den zweiten Weg, weil er nach meiner Auffassung flexibler und universeller ist. Für das in der Einleitung gezeigte Haus sieht meine gekürzte Modelldatei so aus:

# file: house.lst

[S] header [vertices] 16 [triangles] 24 [quads] 0 \
	[tex] false [smooth] false [mat] true

# Vertices:
[S] v [v] 0.0000 5.0000 -3.0000 
[S] v [v] 0.0000 5.0000 3.0000 
[S] v [v] 2.0000 2.0000 -3.0000 
...
[S] v [v] 2.0000 0.0000 -3.0000 
[S] v [v] -2.0000 2.0000 -3.0000 
[S] v [v] -2.0000 0.0000 -3.0000 

# Triangles:
[S] t [i] 0 2 7 [t1] [t2] [n1] [n2] [n3] [N] 0.000 0.000 -1.000 
[S] t [i] 1 6 3 [t1] [t2] [n1] [n2] [n3] [N] 0.000 0.000 1.000 
[S] t [i] 0 1 2 [t1] [t2] [n1] [n2] [n3] [N] 0.832 0.555 0.000 
...
[S] t [i] 8 10 12  [t1] [t2] [n1] [n2] [n3] [N] 0.000 1.000 0.000 
[S] t [i] 9 15 11  [t1] [t2] [n1] [n2] [n3] [N] 0.000 -1.000 0.000 
[S] t [i] 15 13 11 [t1] [t2] [n1] [n2] [n3] [N] 0.000 -1.000 0.000 

# Material:
[S] m [amb] 0.5 0.1 0.1 1.0 [diff] 0.9 0.3 0.1 1.0 [spec] 0.0 0.0 0.0 1.0

Das alles ist recht normal aufgebaut: eine Vertexliste sowie eine Dreiecksliste, die über Indices auf die Vertexliste zurückgreift. Die Texturkoordinaten [t1] und [t2] sind noch nicht eingetragen, da das Testobjekt ohne Textur auskommt. Dasselbe gilt für die Vertexnormalen [n1]...[n3], denn Smooth-Shading ist in der Testphase ebenfalls unerwünscht. Eigentlich könnte auch noch auf die Flächennormale [N] verzichtet werden, denn nach der Skalierung muss sie ohnehin neu berechnet werden. - Das Objekt wurde übrigens mit Milkshape modelliert und mit Hilfe eines kleinen Delphi-Programms in das gezeigte Skript-Format übersetzt. Dieses robuste und leicht auszuwertende Skript-Format verwende ich unter Linux und Windows und nicht nur für Objektbeschreibungen, sondern für Konfigurationsdaten aller Art. Das aber nur am Rande.

Objektbeschreibung

Die Modelldatei bechreibt vor allem die geometrische Struktur. In der Regel möchten wir noch andere Merkmale festlegen, so dass es sinnvoll ist, eine zusätzliche Objektdatei einzuführen, die wie folgt oder ähnlich aufgebaut sein kann:

# file: objects.lst

[name] house [type] 3 [texture] [rad] 5.5 \
[collision] 2 [collect] 0 [model] house.lst [sound] [billboard] [mat] 1

[name] tree1 [type] 2 [texture] tree1.png [rad] 0.8 \
[collision] 1 [collect] 0 [model] tree1.lst [sound] [billboard] [mat] 0
...

[type] ist hier eine grundsätzliche Typisierung. So handelt es sich bei [type] 3 um ein dreidimensionales Objekt, dessen Geometrie in [model] zu finden ist, während [type] 2 ein Objekt beschreibt, das lediglich in Form gekreuzter Texturen gezeichnet wird. Im lezteren Fall enthält [model] einige Parameter wie Form, Höhe, Breite, Fusspunkt usw., eben jene Parameter, die für eine Kollision am Gesamtobjekt von Bedeutung sind.

[texture] verweist auf die zugehörige Texturdatei, sofern eine verwendet wird, und [rad] gibt den Radius der Hüllkugel (bounding sphere) an. [billboard] enthält bei Bedarf den Verweis auf eine Ersatztextur, die bei größerer Entfernung das dreidimensionale Modell auf einfache Sprites reduziert.

Objektinstanzen

Die Daten aller benötigten Objekttypen werden also eingelesen und in ein geeignetes Array übertragen. Damit stehen die allgemeinen Eigenschaften des Objekttyps zur Verfügung. Darüber hinaus benötigen wir eine Datei, in der die alle vorkommenden Objektinstanzen aufgelistet sind. Was dazu gehört, sehen wir sofort, wenn wir uns einen Auszug aus einer Instanzendatei betrachten:

# file: items.lst

[name] house [position] 6.0  0.0 -25.0 \
[scale] 1.2 1.6 1.4 [rotation] 0 30 0 [translation] 0 -0.02 0

[name] tree1 [position] 0.5  0.0  -25.0 \
[scale] 1 1.3 1 [rotation] 0 33 0 [translation] 0 0 0

[name] tree1 [position] 0.78  0.0  -67.0 \
[scale] 1.7 1.1 1.5 [rotation] 0 70 0 [translation] 0 0 -0.4

[name] tree3 [position] 1  0.0  -35.0 \
[scale] 2.0 3.0 2.0 [rotation] 8 120 0 [translation] 0 0 0

Jede einzelne Objektinstanz erhält eine Positions-, Rotations- und Skalierungsangabe, während [name] den Bezug zur Objektbeschreibung herstellt. Mit [translation] kann eine Feinjustierung der Position vorgenommen werden. Die Korrektur ist z.B. nützlich, wenn die Positionsdaten auf die ganzzahligen Pixelpositionen der Heightmap bezogen sind. Unumgänglich ist die Korrektur bei Objekten, die auf abschüssigem Gelände positioniert werden.

Wie gesagt, ohne Kollision könnten wir die Instanzdaten einlesen und mit dem Triple glTranslate, glRotate und glScale direkt die damit verbundenen Objekte zeichnen. Aber für die Kollisionsberechnung benötigen wir die Daten in ihrer endgültigen Form. Das heißt, die Vertexdaten müssen so vorliegen, wie sie sich nach der Verschiebung, Rotation und Skalierung ergeben. Was OpenGL intern durchführt, müssen wir extern ebenfalls erledigen. Nun, das Umrechnen ist kein Problem. Wir machen es genau so wie OpenGL und besorgen uns am besten gleich die passende Matrix von diesem "Matrizenprofi".

        TGLMatrix glmat; // Typ: GLfloat[16]

        glPushMatrix ();
        glLoadIdentity ();
        glTranslatef (pos.x, pos.y, pos.z);     
        glRotatef (rot.x, 1, 0, 0);
        glRotatef (rot.y, 0, 1, 0);
        glRotatef (rot.z, 0, 0, 1);
        glScalef (scale.x, scale.y, scale.z);
        glGetFloatv (GL_MODELVIEW_MATRIX, glmat);
        glPopMatrix ();

Mit dieser Matrix multiplizieren wir die Vertices aller Objektinstanzen und speichern sie in einem strukturierten Array. Bei den Umrechnungen achten wir darauf, dass OpenGL die Matrix nicht zeilenweise, sondern spaltenweise anordnet. Aber ich denke, das wird jeder, der mit GL-Matrizen rechnet, wohl im Hinterkopf haben.

Wir dürfen nicht vergessen, die für die Beleuchtung unerlässlichen Polygonnormalen neu zu berechnen. Die ursprünglichen, von dem 3D-Programm berechneten Normalen sind nach der Skalierung nicht mehr zu gebrauchen. - Wenn wir ohnehin schon die Daten aller vorkommenden Polygone in absoluten Koordinaten vorliegen haben, brauchen wir schließlich beim Rendern nicht mehr das Triple glTranslate, glRotate und glScale zu bemühen, sondern können die im voraus berechneten Daten direkt übergeben. Die Funktion für das Rendern eines einzelnen Objektes könnte etwa so aussehen:

void DrawObjectInstance (TInstance *inst) {
    TVector normal, vert;
    
    if (inst->numTriangles > 0) {
        glBegin (GL_TRIANGLES);
        for (i=0; i < inst->numTriangles; i++) {
            normal = inst->triangles[i].normal;
            glNormal3f (normal.x, normal.y, normal.z);  
            for (j=0; j<3; j++) {
                vert = inst->triangles[i].vertex[j];
                glVertex3f (vert.x, vert.y, vert.z);
            }
        } 
        glEnd ();
    } else if (inst->numQuads > 0) {
    ...
    } else ...
}

Der Parameter inst ist ein Zeiger auf ein Element des Instanzenarrays. Das soll hier als Anregung reichen; wie wir das Array nun im einzelnen gestalten, hängt vom grundsätzlichen Programmaufbau und nicht zuletzt von den Programmiergewohnheiten ab.

Umhüllen und optimieren

Bounding Volumes

Damit komme ich zu den Hüllkörpern (bounding volumes). Wir haben solche Hüllkörper bereits kennengelernt, denn die Kugel und das Ellipsoid, womit wir unser bewegtes Objekt einpacken, gehören dazu. Es gibt verschiedene Arten von Hüllkörpern, über die man sich ruhig ein wenig schlau machen sollte (Stichwörter bounding volume, bounding sphere, bounding cylinder ... Ihr findet auch Infos im Artikel Hüllkörper.). Meistens, so auch in der bisher beschriebenen Anwendung, werden Hüllkörper benutzt, um ein komplexeres Objekt auf eine einfache Form zurückzuführen. Dadurch halten wir die Rechenvorgänge in Grenzen - oder ermöglichen sie überhaupt erst. Hüllkörper werden ferner gebraucht, um statische Kollisionsobjekte zu vereinfachen. So könnte z.B. ein Baumstamm, der aus mehreren Polygonen besteht, als Zylinder betrachtet werden, und die Kollision würde so berechnet, als handle es sich um einen echten, wirklich runden Zylinder.

Im folgenden möchte ich aber auf eine andere Verwendung der bounding volumes eingehen. Sie sind hervorragend geeignet, die Kollisionsberechnung zu optimieren, indem die Zahl der zu untersuchenden Polygone reduziert wird. Ein einfaches Rechenbeispiel: Wir haben eine Szenerie mit rund 1000 Objekten, von denen jedes im Schnitt aus 50 Polygonen zusammengesetzt ist. Das ergibt 50000 Polygone, die wir in jedem Frame untersuchen müssten. Vielleicht schafft der Rechner das, aber viel Luft bleibt nicht mehr.

Wesentlich schneller geht es, wenn wir eine Art Vorselektion durchführen, indem wir zunächst nur prüfen, welche Objekte aufgrund der Entfernung und der Bewegungsrichtung überhaupt in Frage kommen. Wir unterziehen also die 1000 Objekte einer schnellen, eher oberflächlichen Vorprüfung, und die herausgefilterten Objekte werden anschließend für eine exakte Kollisionserkennung an all ihren Polygonen herangezogen. In vielen Fällen wird der bounding volume check überhaupt kein kollisionsfähiges Objekt ausliefern, je nachdem, wie dicht die Landschaft besiedelt ist.

Man liest gelegentlich, dass ein Hüllkörper das Objekt so dicht wie möglich umschließen soll, quasi wie ein Maßanzug. Irgendwie plausibel, aber im Falle der Vorselektion trifft das nicht zu. Im Gegenteil, da wir bestrebt sind, alle in Frage kommenden Objekte zu erfassen, kann der Hüllkörper ruhig etwas großzügig bemessen sein. U.U. werden dann zwar einige Dutzend Polygone zu viel untersucht, was noch besser als eine Kollisionslücke ist. Aus demselben Grunde können wir darauf verzichten, einen maßgerechten Hüllkörper zu wählen und diesen womöglich noch genau auf das Objekt auszurichten. Für unseren Zweck ist die Kugel geeignet, sie ist einfach zu hantieren, ohne Ecken und Kanten. Weiter unten werde ich erläutern, dass evtl. ein Zylinder noch günstiger sein kann.

Testszene mit sichtbar gemachten Hüllkörpern.

Hier war der Verpackungskünstler Christo am Werk. Das Bild zeigt noch einmal die Testszenerie, nun mit umhüllten Objekten. Auf Grund der Bewegungsrichtung der Kugel kommen nur die blau "eingepackten" Objekte in Frage; es muss also nur die Kollision an dem einen, kegelförmigen Baum sowie an den Polygonen des Hauses untersucht werden.

Wie prüfen wir, ob ein Objekt für eine Kollision in Frage kommt? Nun, dazu bietet sich eine übliche Ray-Sphere-Intersection-Funktion an, die wir aber etwas kürzen können. Wir wollen ja lediglich feststellen, ob die Hüllkugel getroffen wird, nicht wo das geschieht. Auf die überflüssige Berechnung der Wurzel verzichten wir und prüfen nur, ob der Ausdruck unter der Wurzel positiv oder negativ ist. Entsprechend der boolsche Rückgabewert.

bool SphereIntersect (TVector center, double rad, 
        TVector p, TVector dir)
{
        TVector q = SubtractVectors (center, p);
        double c = VectorLength (q);
        double v = DotProduct (q, dir);
        double d = rad * rad - (c * c - v * v);

        if (d < 0.0) return false;
        else return true;
}

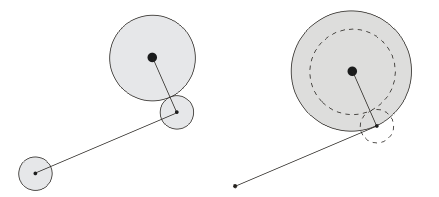
Streng genommen müsste eine Funktion zur Sphere-Sphere-Intersection zum Einsatz kommen, aber da wir uns nicht für den genauen Intersektionspunkt interessieren, geht es mit der gezeigten Ray-Sphere-Intersektion. Wir müssen dann nur den Radius der bewegten Kugel zum Radius der Hüllkugel addieren. Im Falle eines Ellipsoids nehmen wir den größten der 3 Radien.

Vergrößern des Hüllkörpers um eine Ray-Sphere-Intersektion anstatt der Sphere-Sphere-Intersektion verwenden zu können.

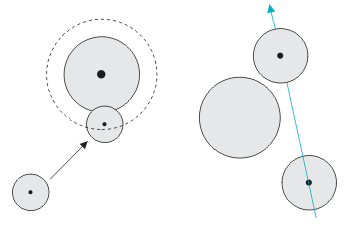
Evtl. kommt ein verkürztes und schnelleres Verfahren in Frage. Dabei prüfen wir lediglich, ob sich nach Durchführung des Bewegungsschrittes das bewegte Objekt im Bereich der Hüllkugel befindet. Das ist nichts anderes als ein schlichter Abstandstest. Eine Kollision kommt dann in Frage, wenn der Abstand der beiden Mittelpunkte kleiner als die Summe der beiden Radien ist. Hierbei brauchen wir ebenfalls keine Wurzelberechnung; es genügt, wenn wir die Quadrate der Entfernungen miteinander vergleichen, da keine negativen Werte vorkommen.

Problemfälle die zu beachten sind. Falls das Objekt zu schnell ist, kann ein Kollisionspunkt "verpasst" werden.

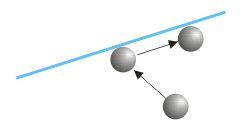
Wir müssen jedoch bedenken, dass dieses Verfahren nicht ganz ohne Tücken ist. Es kann nämlich vorkommen, dass mit einem Bewegungsschritt der Bereich der Hüllkügel bereits überschritten wird (rechts im Bild). Die Gefahr ist umso größer, je schneller sich das Objekt bewegt und je kleiner die Hüllkugel ist. Evtl. können wir uns helfen, indem wir in Abhängigkeit von der Geschwindigkeit die Hüllkugel vergrößern.

Weitere Optimierungen

Die Verwendung von bounding volumes bringt an sich schon einen enormen Gewinn an Performance, doch wir können noch einen Schritt weiter gehen, indem wir die Objekte zusätzlich räumlich eingrenzen. Das lohnt sich aber nur, wenn sich sehr viele Objekte in der Szenerie befinden (> 500 ... 1000), denn der Bounding-Check ist ziemlich schnell und kann einiges verkraften.

Auf die Möglichkeiten der räumlichen Eingrenzung will ich nicht im Detail eingehen. In Frage kommen die üblichen Methoden zur Raumunterteilung. Ob wir die Szenerie einfach in Areale aufteilen oder auf anspruchsvollere Baumstrukturen (BSP-Tree, Quadtree) zurückgreifen, muss von Fall zu Fall geprüft werden. Das hängt von der Größe bzw. Form der Szenerie, der Art der Bewegung innerhalb der Szenerie und nicht zuletzt von den Eigenschaften der Objekte ab.

Mittelpunkt und Radius der Hüllkugel

Schon bei der Gestaltung des Objekts mit dem Modellierprogramm legen wir einen wichtigen Punkt fest; es ist die Stelle mit den Nullkoordinaten. Diese Stelle dient als Bezugspunkt für die Positionierung des Objektes, und auch die Rotation und Skalierung beziehen sich darauf. Um das Objekt bequem positionieren zu können, legen wir den Nullpunkt am besten so, dass er in der Mitte der Grundfläche zu liegen kommt. Er ist quasi der Fußpunkt des Objektes.

Der Fußpunkt des Hauses liegt im Zentrum des Fundaments.

Den Mittelpunkt der Hüllkugel dagegen würden wir spontan ins Zentrum des Körpers legen, so wie es in der Abbildung oben dargestellt ist. Es ist aber günstiger, den Fußpunkt (Rotationspunkt) als Mittelpunkt zu nehmen. Das nächste Bild zeigt, warum.

Wird das Objekt ohne den Hüllkörper rotiert, kann es aus diesem herausragen. Wählt man den Fusspunkt ist der Körper auch nach Rotationen noch innen. Nachteil ist der größere Hüllkörper. Rotiert man den Hüllkörper jeweils mit um den Rotationspunkt/Fusspunkt kann Variante 1 kleinere Hüllkörper liefern.

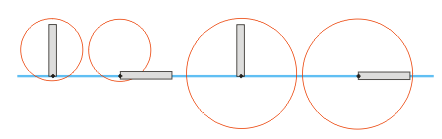
Wenn wir das Instanzenarray berechnen, müssen wir mit dem Objekt auch den Radius der Hüllkügel entsprechend skalieren. Sofern wir in den drei Dimensionen unterschiedlich skalieren, nehmen wir den größten der drei Skalierungsfaktoren.

Eine Hüllkugel begrenzt den Raum in allen Richtungen, auch nach oben und unten. Wenn die Objekte vor allem nebeneinander in der Szenerie angeordnet sind, ist die Begrenzung nach oben und unten nicht erforderlich. Die Öffnung führt dazu, dass wir einen (unendlichen) Zylinder als boundig volume verwenden. Da wir die Höhe nicht beachten, läuft es auf eine zweidimensionale Berechnung hinaus. Anstelle der Kugel tritt nun ein Kreis (bounding circle). Evtl. kann eine solche Vereinfachung sogar Vorteile haben, wie das nachfolgende Bild zeigt. Der Radius lässt sich dadurch verringen:

Verwendung eines "Bounding-Circles" der unendlich nach oben und unten ragt. Mitunter liegt durch diese Variante der Hüllkörper näher am Objekt.

Die Berechnung erfolgt ähnlich wie bei der Hüllkugel, nur dass wir die Y-Koordinate nun unbeachtet lassen, indem wir sie immer auf 0 stellen.

Nun noch die Polygone des Terrains

Bis jetzt haben wir nur die Polygone der aufgesetzten Objekte betrachtet. Aber es kommen ja noch die Dreiecke des Untergrundes hinzu, die wir wahrscheinlich in einem Vertex-Array deponiert haben. Es versteht sich, dass wir ebenfalls die Zahl der Polygone weitgehend reduzieren müssen. Das geschieht natürlich nicht mit Hüllkörpern, sondern einfach durch räumliche Eingrenzung. Wir testen, welche Teile des Terrains von dem Bewegungsschritt betroffen sind und holen uns die entsprechenden Dreiecke aus dem Array.

Links zwei mögliche Anordung der Dreiecke in einem Raster. Rechts das Prinzip nachdem die betroffenen Quads ermittelt werden. Der orange Rahmen beschreibt die Quads welche geprüft werden müssen.

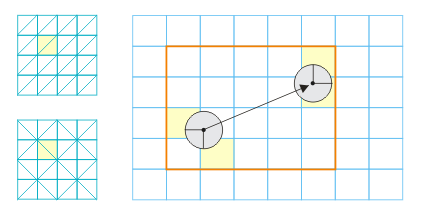
Zunächst ein kleiner Blick auf die mögliche Anordnung der Dreiecke. Links oben sehen wir eine regelmäßige Anordnung, darunter eine alternierende Anordnung, die wir häufig in Verbindung mit dem Quadtree-Verfahren vorfinden. So oder so, zu einem Quadranten gehören immer zwei Dreiecke. Wir müssen nur aufpassen, dass wir die richtigen Vertices aus dem Netz herausfischen.

Im rechten Teil ist eine Möglichkeit der Eingrenzung skizziert. Wir müssen lediglich die Min-Max-Werte für die Zeilen bzw. Spalten ermitteln und können den Bereich dann in einer Doppelschleife abarbeiten. Dabei werden einige Quadranten erfasst, die außerhalb der Bahn liegen, aber ich bezweifle, dass es sich lohnt, diese auszuklammern. Immerhin ist der Bereich relativ begrenzt - oder sollte es sein. Wenn nämlich sehr viele Quadranten in einem einzigen Schritt überstrichen werden, gerät der ganze Algorithmus an seine Grenzen. Siehe meine Bemerkung am Ende.

Es klemmt - und ein wenig Physik

Kraft und Bewegung

Hat von den Lesern des 2. Tutorials schon jemand darüber geschimpft, dass die Kugel sich nicht mehr bewegt, wenn man sie gegen den Boden oder eine Wand steuert? Zugegeben, das ist wirklich nicht schön. Ich könnte nun boshaft sein und sagen: "Lass die Taste einfach los, dann bewegt sich die Kugel wieder." Aber was ist, wenn eine andere Kraft die Kugel gegen den Boden drückt, z.B. die Schwerkraft? Schwerelosigkeit verträgt sich schlecht mit einem bodenständigen Gleiten über holpriges Gelände.

Wir merken schon, da kommt die Physik ins Spiel. Tatsächlich ist es so, dass die Physik-Engine und der geometrische Kollisionsmechanismus eng zusammenarbeiten, ja, dass die Kollision oft sogar Teil der Physik-Engine ist. Trotzdem muss ich versuchen, die physikalischen Überlegungen auf das absolut Notwendige zu beschränken, sonst wird aus dem dreiteiligen Tutorial noch ein sechsteiliges. Das möchte ich euch lieber ersparen. Ich belasse es also bei einigen Hinweisen und hoffe, dass sie euch ein wenig auf die richtige Spur bringen, wenn's dann zur Sache geht.

Die wichtigsten Zusammenhänge werden durch die folgende, weitgehend bekannte Formel beschrieben:

Kraft als Produkt aus Masse und Beschleunigung, natürlich auf Vektorbasis. Anders ausgedrückt: Kraft und Beschleunigung sind proportional, mit der Masse als konstantem Faktor. Damit können wir schon eine Menge in den Griff bekommen. Wenn wir die verschiedenen Kräfte, die auf das bewegte Objekt einwirken, kennen und im richtigen Verhältnis addieren, wissen wir, welche Beschleunigung das Objekt erfährt. Setzen wir ferner voraus, dass in einem Zeitintervall eine gleichförmige Bewegung vorliegt und somit Geschwindigkeit und Weg proportional sind, erhalten wir den neuen Bewegungsvektor durch Addition des entsprechend skalierten Kraftvektors.

Jede Kraft hat eine typische Richtung. Die Reibung wirkt z.B. der Bewegungsrichtung entgegen, ebenso eine künstlich erzeugte Bremskraft. Schubkräfte wirken parallel zur Bewegungsrichtung oder - besser gesagt - in der Richtung, in der wir das Objekt steuern wollen. Das muss nicht unbedingt übereinstimmen, z.B. bei Windeinflüssen, die wir zweckmäßigerweise mit dem Luftwiderstand kombinieren. Eindeutig ist die Gravitationskraft: Sie zeigt nach unten und ist das Produkt aus Masse und Erdbeschleunigung (9.81 m/s/s). Es ist natürlich Unsinn, im Programm mit dieser genauen, physikalischen Größe zu arbeiten; vielmehr werden wir einfach die Masse auf einen geeigneten Wert setzen. Am Rande möchte ich empfehlen, die Masse einstellbar zu machen. Da kann man sehr schön beobachten, wie sich das Bewegungsverhalten mit der Masse ändert. Im übrigen sollte die Masse bei allen beschleunigungswirksamen Kräften berücksichtigt werden.

Mathematisch gesehen haben wir es bei diesen Zusammenhängen mit verschiedenen Ableitungsebenen zu tun. Da gibt es neben der Stammfunktion (Weg) die 1. Ableitung (Geschwindigkeit) sowie die 2. Ableitung (Beschleunigung). Doch wie gesagt, bei dem einfachen Bewegungsmodell mit gleichförmigen Bewegungsschritten von Frame zu Frame brauchen wir keine mathematischen Klimmzüge zu machen. Anders allerdings, wenn wir exakte Bewegungsabläufe zwischen den Frames berechnen wollen oder müssen. Dann kann es sein, dass wir wegen des Aufeinanderstoßens der verschiedenen Ableitungsebenen auf Differentialgleichungen stoßen. Als Lösung bietet sich ein ODE-Solver an, ein Algorithmus zur numerischen Lösung solcher Gleichungen.

Kollisionsbremsen

Nach dem kleinen Ausflug in die Physik nun aber schnell zurück zur Kollision. Die Frage war ja, warum sich ein Objekt nicht mehr bewegt, wenn es durch eine Kraft gegen ein Polygon gedrückt wird. Das folgende Bild zeigt den Grund:

Der Grund wieso Objekte nicht an Kollisionsflächen entlangrollen: Der Kollisionspunkt kollidiert sofort wieder. Das Objekt bleibt am Kollisionspunkt liegen, d.h. es bewegt sich nicht.

Schon an der ursprünglichen Position (oder in ihrer unmittelbaren Nähe) gibt es bereits eine Kollision mit dem Polygon, und da wir - bisher jedenfalls - die Kugel nur bis zum Kollisionspunkt bewegt haben, kommt sie logischerweise nicht von der Stelle. Also ein durchaus erklärbares Verhalten. Aber was ist zu tun? Auf keinen Fall sollten wir das Objekt nach der Berechnung des Gleitpfades sofort in die neu berechnete Richtung bewegen, denn es kann sich ja ein weiteres Hindernis auftun.

Grundregel: Vor jeder Bewegung muss eine Kollisionserkennung erfolgen, und wenn eine Kollision festgestellt wird, darf das Objekt nur bis zum Kollisionspunkt bewegt werden.

Folglich müssen wir u.U. mehrere Kollisionserkennungen innerhalb eines Frames durchführen, solange, bis der Weg frei ist und der Bewegungsschritt zum Abschluss gebracht werden kann. Dabei empfiehlt es sich, die Geschwindigkeit in Abhängigkeit vom Aufprallwinkel herabzusetzen (siehe "Kollisionsverarbeitung" im 2. Teil des Tutorials). Es kann ja passieren, dass das Objekt nicht ohne weiteres frei kommt. Die Gefahr, dass wir in eine Endlosschleife geraten, umgehen wir, indem wir den Vorgang beim Erreichen einer Minimalgeschwindigkeit abbrechen. Alternativ oder zusätzlich können wir die Anzahl der Kollisionserkennungen pro Frame begrenzen (vielleicht 4 oder 5). Wie auch immer, wenn das Objekt sich nicht befreien kann, muss es in eine völlig andere Richtung gewiesen werden.

Durch die Mehrfacherkennung wird gleichzeitig die bremsende Wirkung der Gravitation (oder sonstiger Steuerimpulse) reduziert, denn sie geht nur in den Bewegungsvektor der ersten Kollisionserkennung ein. Bei den Folgeerkennungen ist dann nur noch der geometrisch berechnete Gleitpfad wirksam. Das führt aber dazu, dass die Gravitation u.U. gar nicht zur Geltung kommt. Es bringt auch nichts, die Gravitation bei jeder Kollisionsberechnung erneut ins Spiel zu bringen, denn dabei bliebe das Objekt permanent kleben. Damit sich das Objekt überhaupt befreien kann, dürfen wir die Gravitation und die anderen Kräfte erst am Schluss addieren. Wir berechnen dann noch einmal eine Kollision nur mit den zusätzlichen Kraftvektoren, bestimmen auch den neuen Gleitpfad, reduzieren aber nicht mehr die Geschwindigkeit.

Die Gravitation und vergleichbare Kräfte dürfen erst am Ende addiert werden. Nicht nur bei Abhängen, sondern auch auf der Geraden.

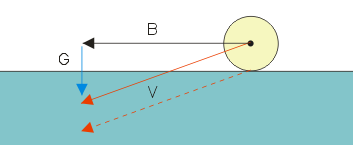
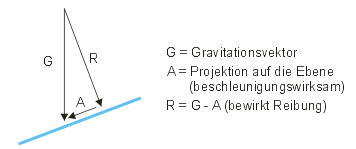
In diesem Zusammenhang sollten wir kurz überlegen, welche Einfluss die Gravitation hat. Natürlich, sie sorgt für eine Richtungsänderung nach unten, aber das ist noch nicht alles. Die Gravitation hat neben der Bodenbeschaffenheit einen Einfluss auf die Reibung, und vor allem sorgt sie auf abschüssigem oder ansteigendem Gelände für Beschleunigungen bzw. Verzögerungen. Um den beschleunigungswirksamen Anteil des Gravitationsvektors zu ermitteln, projizieren wir ihn auf die Ebene des Untergrundpolygons und erhalten auf diese Weise zwei Teilvektoren. Der eine zeigt senkrecht auf den Untergrund und kann zur Berechnung der Reibung benutzt werden, während der andere Teilvektor den Bewegungsvektor direkt beeinflusst.

Durch die Projektion der Gravitation auf die Ebene des Abhangs erhält man die Hangabtriebskraft.

Ich weiß, dass alles sind nur Gedankenanstöße, aber mehr kann ich in diesem Rahmen nicht bieten. Inwieweit wir die physikalischen Faktoren berücksichtigen, hängt ohnehin von der jeweiligen Programmsituation ab. Nehmen wir als Beispiel ein Autorennen. Hier ist die Gravitationskraft so groß, dass sich das Gefährt nicht vom Boden löst, von extremen Crashes einmal abgesehen. Da stellt sich die Frage, ob man überhaupt die Gravitation einbeziehen soll. Wahrscheinlich wird es reichen, nach jedem Bewegungsschritt das Fahrzeug auf den Untergrund zu stellen und an dessen Normale auszurichten, damit alle 4 Räder Bodenhaftung bekommen.

Wo liegen die Grenzen des Verfahrens?

Nun, es ist offensichtlich, dass das Verfahren nur zu gebrauchen ist, wenn das bewegte Objekt - schön abgerundet zu einer Kugel oder einem Ellipsoid - als Ganzes kollidiert. Sobald das Objekt aber Ecken und Kanten hat, die in verschiedener Weise anstoßen können, müssen wir zu differenzierteren Verfahren greifen, auf die ich hier nicht eingehen kann.

Darüber hinaus es gibt weitere Einschränkungen. So kann es z.B. zu Problemen kommen, wenn sich innerhalb eines Zeitintervalls bedeutsame Änderungen ergeben. Das kann der Fall bei mehreren bewegten Objekten sein, die miteinander kollidieren können und ihre Wege in der Zwischenzeit kreuzen. Das kann aber auch der Fall sein, wenn in einem Intervall viele Terrainpolygone überquert werden. Dann ist das "Zeitnetz" zu grobmaschig gegenüber dem räumlichen Netz der Szenerie. Große Geschwindigkeiten oder eine sehr hohe Auflösung des Mesh sind die Hauptursachen. Das heißt nicht, dass der Bewegungsablauf gleich aus den Fugen gerät, aber es läuft eher holprig und sprunghaft ab, nicht mehr so geschmeidig. Außerdem lässt sich das Objekt schlechter steuern. Was die Auflösung des Mesh betrifft, müssen wir einen Kompromiss akzeptieren. Einerseits sorgt eine hohe Auflösung für eine detaillierte und angenehme Landschaftsdarstellung; andererseits ist der Bewegungsablauf flüssiger bei großflächigen Terrain-Polygonen.

Für Abhilfe sorgt ggfs. eine Unterteilung des Zeitintervalls. In jedem Frame werden mehrere Weg-Zeit-Marken bearbeitet, wobei die Anzahl hauptsächlich von der Geschwindigkeit abhängt. Nach jedem Teilintervall erfolgt eine komplette Kollisionsberechnung mit interpolierten Parametern. Evtl. kann dabei der oben erwähnte ODE-Solver erforderlich werden. Der Rechenaufwand im ODE-Solver ist beachtlich, aber andererseits kann ein gut eingestellter Solver die Kollisionsberechnungen vereinfachen bzw. beschleunigen, weil an die Intersektions-Funktionen geringere Anforderungen gestellt werden.

Ja, ich weiß, eigentlich geht es jetzt erst richtig los, aber irgendwann muss ich einen Schlusspunkt setzen. Punkt.

Ich wünsche euch allen viel Spaß beim Kollidieren und viele gute Ideen. Die braucht ihr ganz bestimmt, wenn ihr eine Kollision in euer Programm einbauen wollt.

Reinhard

Vorhergehendes Tutorial: Tutorial Kollision2	Zur Übersicht	Nächstes Tutorial: -
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen.