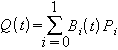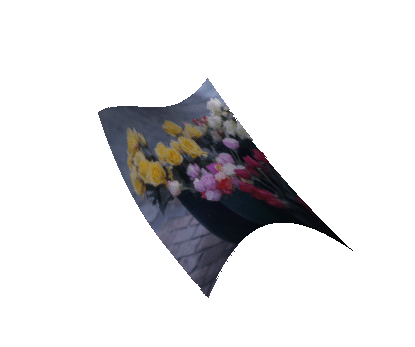Tutorial Abseits eckiger Welten

Abseits eckiger Welten

Einführung

Unsere Welt ist, schlecht, eintönig und eckig. Wirklich? Eckig? Schauen wir uns noch einmal um. An vielen Stellen ja, aber nicht überall. Rundungen sind sogar recht häufig anzutreffen. Ein Blick um mich herum offenbart es. Maus, Lampe, Joystick,... Vieles hat Rundungen. Ein Blick auf das was bisher bei DGL zu sehen war, zeigt: alles eckig :-(. Das muss geändert werden. Runden wir unsere Virtuellen Welten ein wenig ab - unser Hilfsmittel: Curved Surfaces

Von Linien und Kurven

Dies Kaptitel basiert auf Curved Surfaces Using Bézier Patches von Gabe Kruger. Übersetzt ins deutsche und natürlich mit der ein oder anderen Änderung.

Prozedurale Linien

Gerade Strecken lassen sich allein durch die Angabe eines Start und Endpunktes beschreiben. Mit einer Liniengleichung lassen sich beliebig viele Punkte auf dieser Strecke berechnen. Eine solche Gleichung ist z.B.:

   Q(t) = (1 - t)*P0 + t*P1

Der Parameter t hat dabei Werte von 0 bis 1. P₀ und P₁ sind die Endpunkte der Strecke. Setzt man den Parameter t = 0 ein, so ist das Ergebnis P₀. Setzt man 1 ein ist das Ergebnis P₁. Die Gleichung könnte man etwas umschreiben:

   Q(t) = B0(t)*P0 + B1(t)*P1

Wobei gilt:

   B0(t) = 1 - t
   B1(t) = t

Man nennt B₀(t) und B₁(t) die Basis Funktionen der Liniengleichung. Ändern wir diese Gleichung nochmals ein wenig ab:

Dies ist die analytisch bearbeitete Fassung der Liniengleichung, die meisten Beschreibungen parametrischer Kurven werden in dieser Form gezeigt. Kurven? Klingt so als wären wir bereits am Ziel? Fast.

Evolution zu Bezier Kurven

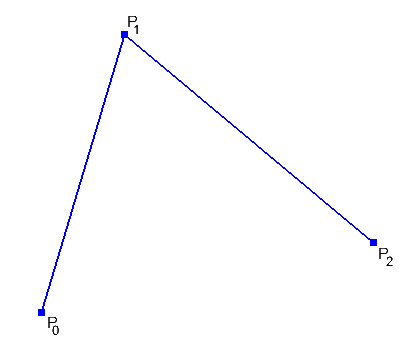
Wie erzeugen wir nun eine Kurve in parametrischer Form, ählich der obigen? Wir wollen eine Kurve beschreiben, die durch die Endpunkte geht und dazwischen sich einem anderen Punkt annähert:

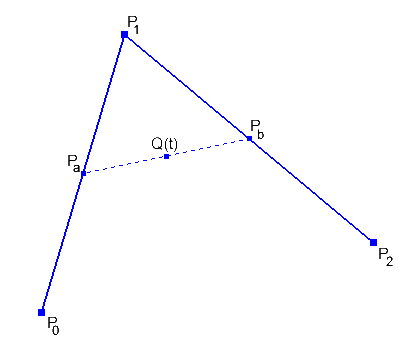
P₀ und P₂ sind die Endpunkte, P₁ ist der Kontrollpunkt, dem wir uns annähern wollen. Man könnte nun einen Punkt P_a(t) zwischen P₀ und P₁ interpolieren und das gleiche mit einem Punkt P_b(t) zwischen P₁ und P₂. Der gewünschte Punkt Q(t) auf der Kurve kann dann errechnet werden, durch interpolieren zwischen den Punkten P_a und P_b:

In mathematischen Formeln ausgedrückt:

   Pa(t) = (1 - t)P0 + t * P1
   Pb(t) = (1 - t)P1 + t * P2

   Q(t)  = (1 - t)Pa(t) + tPb(t) =
         = (1 - t)²P0 + 2(1 - t)tP1 + t²P2

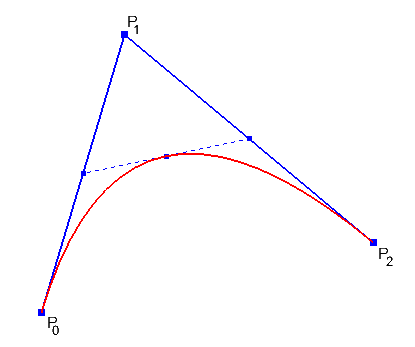
Der Lohn der Mühen:

Wir können nun die Gleichung von oben umschreiben:

Nun haben wir eine Definition einer quadratischen Bézier Kurve entwickelt. Es gibt eine einfache Formel für die Basis Funktionen von Bezier Kurven für einen beliebigen Grad. n ist der Grad, i beziffert die Basis Funktion und reicht damit von 0 bis n:

Ein Beispiel einer solchen Kurve mit dem Grad 3:

Evaluators

Wir können jetzt Bezier Kurven von Hand berechnen und, mit etwas Umsicht das ganze von 2D auf 3D transformieren. Das kann man vielseitig einsetzen und man kann gleichzeitig auf Detaileinstellungen in einem Programm reagieren - je höher der Detailgrad, desto feiner werden die Kurven aufgelöst. Ebenso kann man sie schön für Kamerafahrten verwenden.

Interessant ist jedoch, dass OpenGl auch die Möglichkeit besitzt, solche Kurven selber zu rendern. In reinem OpenGl kann man hier Evaluators verwenden.

Erster Versuch: Evaluator Kurve

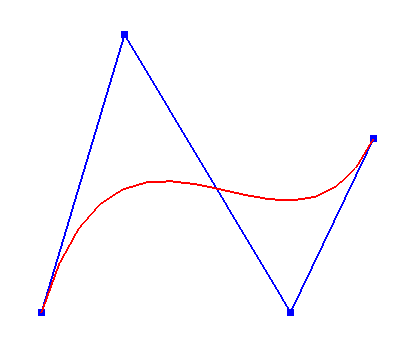
Als erstes wollen wir versuchen einen kubischen Bézier mit OpenGL Evaluators zu zeichnen. Definieren wir zuerst einmal 4 Kontrollpunkte:

    const
      ctrlpoints : Array[0..3] of Array[0..2] of TGlFloat =
       ((-4.0, 2.0, 0.0),(-2.0, 4.0, 0.0),(2.0, -4.0, 0.0),(4.0, 2.0, 0.0));

Der nächste Schritt ist das Übergeben der Punkte an OpenGL:

    glMap1f(GL_MAP1_VERTEX_3, 0, 1.0, 3, 4, @ctrlpoints[0,0]);
    glEnable(GL_MAP1_VERTEX_3);

Kleine Erklärung von glMap1f:

Die 1 steht dafür, dass wir eine Linie beschreiben wollen. Eine 2, also glMap2f stünde für eine Fläche. Der erste Parameter beschreibt den Typ an Daten, den wir übergeben - in unserem Fall also dreidimensionale Vertexkoordinaten. Die nächsten 2 Parameter u₁ und u₂ beschreiben den Start- und Endwert unserer Kurve. Sie beschreiben sozusagen die Werte, die der Parameter t aus dem vorigen Kapitel haben muss, um eine komplette Kurve zu beschreiben. Der Parameter stride sagt aus, wie viele Floats vom Startfloat des einen Kontroll- bis zum Startfloat des nächsten Kontrollpunkts liegen. In unserem Fall also 3(Wegen Array[0..2] - hat 3 Elemente). Der vorletzte Parameter order sagt aus, wie viele Kontrollpunkte wir übergeben wollen. Zu guter Letzt noch ein Pointer auf die Kontrollpunkte, und wir haben unsere Schuldigkeit getan.

Wir haben nun zwei Möglichkeiten unseren Evaluator zu zeichnen. Die erste:

    var
      i : Integer;
      ...
      glBegin(GL_LINE_STRIP);
        for i := 0 to 30 do
          glEvalCoord1f(i/30);
      glEnd;
      ...

glEvalCoord1f erzeugt die Vertexdaten, die wir mittels glMap1f genauer definiert haben (diesmal also nur Vertexpositionen, keine Farben, keine Texturkoordinaten, etc.). Als Parameter werden Werte zwischen u₁ und u₂ eingesetzt.

Es gibt noch eine andere Methode, mit der man die Daten in einem Rutsch an OpenGL weitergeben kann:

    glMapGrid1f(30, 0.0, 1.0);
    //...
    glEvalMesh1(GL_LINE, 0, 30);

Mit glMapGrid1f stellen wir ein, in wieviele Segmente wir unsere Linie unterteilen wollen und übergeben gleichzeitig den Bereich in der Kurve u₁ und u₂.</p>

glEvalMesh1 zeichnet nun unser gutes Stück als Linie. Gezeichnet werden alle Segmente von 0 bis 30.

Von Linien zu Flächen

Die bisherigen Ergebnisse sind noch nicht wirklich überzeugend. Unser Ziel war es immerhin Oberflächen zu zeichnen und keine Linien. Aber weit entfernt sind wir nicht mehr. Beginnen wir damit, wieder unsere Kontrollpunkte zu definieren:

  var
    CtrlPoints2D : Array[0..3] of Array[0..3] of Array[0..2] of TGlFloat;

Diesmal eine Variable? Ist er krank? Seit wann benutzt er Variablen? Nun ich kanns euch erklären: Ich habe mit mehreren unterschiedlichen Flächen herumgespielt und wollte nicht ständig dabei am Code herumbasteln, also habe ich mir fix eine Routine zum Laden der Punkte geschrieben:

    procedure LoadCtrlPoints;
    var
      u, v : Integer;
      F : Text;
    begin
      AssignFile(F, 'surface.txt');
      Reset(F);
      FillChar(CtrlPoints2D[0,0,0], SizeOf(CtrlPoints2D), 0);
      for u := 0 to 3 do
        for v := 0 to 3 do
          ReadLn(F, CtrlPoints2D[u,v,0], CtrlPoints2D[u,v,1], CtrlPoints2D[u,v,2]);
      CloseFile(F)
    end;

Ist die billigste Variante, ohne jeglichen Fehlerschutz, aber fürs herumspielen sollte das genügen. Sobald wir unsere Kontrollpunkte geladen haben, sollten wir sie an OpenGL übergeben:

    LoadCtrlPoints;
    glMap2f(GL_MAP2_VERTEX_3, 0.0, 1.0, 3, 4, 0.0, 1.0, 12, 4, @CtrlPoints2D[0,0,0]);
    glEnable(GL_MAP2_VERTEX_3);
    glEnable(GL_AUTO_NORMAL);
    glEnable(GL_NORMALIZE);
    glMapGrid2f(40, 0.0, 1.0, 40, 0.0, 1.0);

Die glMap2f Funktionen haben jetzt ein paar neue Parameter erhalten. Dies sind an sich die gleichen Parameter wie bei den glMap1f Funktionen, nur dass sie nun doppelt vorhanden sind, für die v Richtung.

Schlussendlich wollen wir noch unsere Oberflächen anzeigen:

    glEvalMesh2(GL_FILL, 0, 40, 0, 40);

Hat die Datei "surface.txt" nun folgenden Inhalt:

   -1.5 2.0 -1.5
   -0.5 -1.0 -1.5
   0.5 -1.0 -1.5
   1.5 -2.0 -1.5
   -1.5 2.0 -0.5
   -0.5 1.0 -0.5
   0.5 -2.0 -0.5
   1.5 0.0 -0.5
   -1.5 0.0 0.5
   -0.5 0.0 0.5
   0.5 0.0 0.5
   1.5 0.0 0.5
   -1.5 1.0 1.5
   -0.5 0.0 1.5
   0.5 -1.0 1.5
   3.0 -2.0 1.5
 

dann könnte das enstehende Bild so aussehen:

Texturen und anderes Feintuning

Es ist schon bemerkenswert, wie leicht man Curved Surfaces in OpenGL zeichnen kann. Was fehlt, ist die Möglichkeit, die Flächen, die man erzeugt hat, auch noch zu texturieren. Jedem dürfte klar sein, was das für Vorteile hat.

Das schöne ist, dass man die Texturierung mit den gleichen Mitteln lösen kann, wie die Oberflächen selbst - mit Evaluators. Definieren wir uns also zuerst einmal ein paar Kontrollpunkte:

    const
      TexCoords : Array[0..1, 0..1, 0..1] of TGlFloat =
        (((0.0, 0.0),(0.0, 1.0)), ((1.0, 0.0),(1.0, 1.0)));

und übergeben die Koordinaten an OpenGL:

    LoadCtrlPoints;
    glMap2f(GL_MAP2_VERTEX_3, 0.0, 1.0, 3, 4, 0.0, 1.0, 12, 4, @CtrlPoints2D[0,0,0]);

    LoadDevilTexture('flowers256.tga');
    glMap2f(GL_MAP2_TEXTURE_COORD_2, 0.0, 1.0, 2, 2, 0.0, 1.0, 4, 2, @TexCoords[0,0,0]);
    glEnable(GL_MAP2_TEXTURE_COORD_2);

    glEnable(GL_MAP2_VERTEX_3);
    glEnable(GL_AUTO_NORMAL);
    glEnable(GL_NORMALIZE);
    glMapGrid2f(40, 0.0, 1.0, 40, 0.0, 1.0);

Wenn wir jetzt mittels glEvalMesh2(GL_FILL, 0, 40, 0, 40) die Szene rendern, bekommen wir das obige Bild. Simpel, nicht?

Noch viel schöner wirds, wenn man feststellt, dass das gleiche nicht nur mit Texturkoordinaten funktioniert. Hier mal eine kleine Übersicht über die Parameter von glMapxf:

Konstante:	Parameter:
GL_MAPx_VERTEX_3	x,y,z Vertex-Koordinaten
GL_MAPx_VERTEX_4	x,y,z,w Vertex-Koordinaten
GL_MAPx_INDEX	Farb-Index Werte
GL_MAPx_COLOR_4	R,G,B,A Farbwerte
GL_MAPx_NORMAL	Normalen-Richtungen
GL_MAPx_TEXTURE_COORD_1	s Textur-Koordinaten
GL_MAPx_TEXTURE_COORD_2	s,t Textur-Koordinaten
GL_MAPx_TEXTURE_COORD_3	s,t,r Textur-Koordinaten
GL_MAPx_TEXTURE_COORD_4	s,t,r,q Textur-Koordinaten

NURBs

Die OpenGL NURBs sind Teil der GL Utilities und damit bei jeder OpenGL-Implementation dabei. Im Redbook finden sich einige sehr schöne Beispiele, die die Verwendung von Nurbs zeigen. Eine Sache, die die NURBs interessant macht, ist die Möglichkeit sie trimmen zu können. Darunter fällt z.B. das Schneiden von Löchern mitten in die Fläche. Eine genaue Besprechung von NURBs würde den Rahmen dieses kleinen Tutorials sicher bei weitem sprengen, so dass ich beschließe hier meine kleine Einführung in das Thema Curved Surfaces zu beenden.

Delphic

Vorhergehendes Tutorial: -	Zur Übersicht	Nächstes Tutorial: Tutorial_Selection
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen.