Bresenham-Algorithmus: Unterschied zwischen den Versionen
Aus DGL Wiki
Flash (Diskussion | Beiträge) (kurzzusammenfassung und verweis auf Wikipedia.) |
K (Kategorisierung & kleinere Tippfehler.) |
||
| Zeile 1: | Zeile 1: | ||
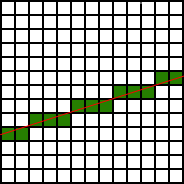
[[Bild:Bresenham.png|thumb|right|Annäherung einer Linie auf einer Rasterausgabe durch den Bresenham-Algorithmus.]] | [[Bild:Bresenham.png|thumb|right|Annäherung einer Linie auf einer Rasterausgabe durch den Bresenham-Algorithmus.]] | ||
| − | Der Bresenham Algorithmus ist ein Scanline-Algorithmus zum Zeichnen von Geraden und Kreisen auf Rasterausgabegeräten. Der Algorithmus ist ein Quasistandard und wird auch von OpenGL benutzt. Er ist benannt nach Jack Bresenham der ihn 1962 bei seiner Tätigkeit bei IBM entwickelte. | + | Der Bresenham-Algorithmus ist ein Scanline-Algorithmus zum Zeichnen von Geraden und Kreisen auf Rasterausgabegeräten. Der Algorithmus ist ein Quasistandard und wird auch von [[OpenGL]] benutzt. Er ist benannt nach Jack Bresenham, der ihn 1962 bei seiner Tätigkeit bei IBM entwickelte. |
| − | Um das Internet mit Redundanzen nicht zu überfüllen verweisen wir hier auf die ausführlichen Artikel bei Wikipedia: | + | Um das Internet mit Redundanzen nicht zu überfüllen, verweisen wir hier auf die ausführlichen Artikel bei Wikipedia: |
| − | [http://de.wikipedia.org/wiki/Bresenham-Algorithmus | + | *[http://de.wikipedia.org/wiki/Bresenham-Algorithmus Deutscher Wikipediaartikel zum Bresenham-Algorithmus]<br> |
| − | [http://de.wikipedia.org/wiki/Bresenham | + | *[http://de.wikipedia.org/wiki/Bresenham Deutscher Wikipediaartikel zu Jack Bresenham] |
| + | |||
| + | [[Kategorie:Technik_oder_Algorithmus]] | ||
Aktuelle Version vom 3. Mai 2008, 15:27 Uhr
Der Bresenham-Algorithmus ist ein Scanline-Algorithmus zum Zeichnen von Geraden und Kreisen auf Rasterausgabegeräten. Der Algorithmus ist ein Quasistandard und wird auch von OpenGL benutzt. Er ist benannt nach Jack Bresenham, der ihn 1962 bei seiner Tätigkeit bei IBM entwickelte.
Um das Internet mit Redundanzen nicht zu überfüllen, verweisen wir hier auf die ausführlichen Artikel bei Wikipedia: