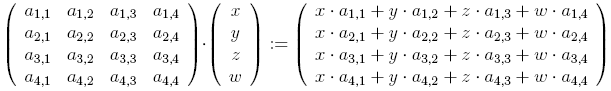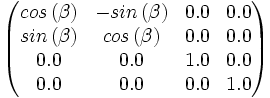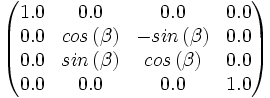Tutorial Nachsitzen: Unterschied zwischen den Versionen
K (Rechtschreibfehler ausgebessert) |
|||
| (28 dazwischenliegende Versionen von 9 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Vorwort== | ==Vorwort== | ||
| − | Immer wieder muss ich feststellen, dass viele die (mit OpenGl) 3D Anwendungen schreiben, nichts mit der Mathematik dahinter anfangen können. Um das | + | Immer wieder muss ich feststellen, dass viele, die (mit OpenGl) 3D Anwendungen schreiben, nichts mit der Mathematik dahinter anfangen können. Um das Ein oder Andere zu verstehen oder sich selbst überlegen zu können, ist dieses Wissen aber unabdingbar. Ich möchte mit diesem Artikel helfen, diesen Zustand zu beenden und entsprechends Wissen unter euch verbreiten. Dies und |
| + | das werded ihr aus der Schule kennen, wenn ihr also etwas überspringen wollt, orientiert euch an den Überschriften. | ||
==Trigonometrie am rechtwinkligen Dreieck== | ==Trigonometrie am rechtwinkligen Dreieck== | ||
| Zeile 7: | Zeile 8: | ||
[[Bild:Tutorial_Nachsitzen_einheitskreis.gif]] | [[Bild:Tutorial_Nachsitzen_einheitskreis.gif]] | ||
| − | An der x-Achse bildet sich dann ein rechter Winkel(wichtig für normale Trigonometrie). Die diesem Winkel gegenüberliegende Seite(r) nennt man Hypotenuse. Die am Winkel ß anliegende Seite(x) ist die Ankathete. Die dem Winkel gegenüberliegende Seite(y) heißt Gegenkathete. | + | An der x-Achse bildet sich dann ein rechter Winkel (wichtig für normale Trigonometrie). Die diesem Winkel gegenüberliegende Seite(r) nennt man Hypotenuse. Die am Winkel ß anliegende Seite(x) ist die Ankathete. Die dem Winkel gegenüberliegende Seite(y) heißt Gegenkathete. Man definiert folgende Funktionen: |
| − | <pascal> | + | <source lang="pascal"> |
sin(ß) = Gegenkathete / Hypotenuse | sin(ß) = Gegenkathete / Hypotenuse | ||
cos(ß) = Ankathete / Hypotenuse | cos(ß) = Ankathete / Hypotenuse | ||
tan(ß) = Gegenkathete / Ankathete | tan(ß) = Gegenkathete / Ankathete | ||
| − | </ | + | </source> |
Im Einheitskreis(und nur dort) gilt: | Im Einheitskreis(und nur dort) gilt: | ||
| − | <pascal> | + | <source lang="pascal"> |
sin(ß) = y | sin(ß) = y | ||
cos(ß) = x | cos(ß) = x | ||
| − | </ | + | </source> |
| − | da die | + | da die Länge der Hypotenuse 1 ist(Kreisradius). |
| − | Die Umkehrfunktionen dazu sind(in Pascal): | + | Die Umkehrfunktionen dazu sind (in Pascal): |
| − | <pascal> | + | <source lang="pascal"> |
ß = arcsin(sin(ß)) | ß = arcsin(sin(ß)) | ||
ß = arccos(cos(ß)) | ß = arccos(cos(ß)) | ||
ß = arctan(tan(ß)) | ß = arctan(tan(ß)) | ||
| − | </ | + | </source> |
| − | für ß im | + | für ß im Bereich 0° - 90°. In den anderen Quadranten des Koordinatensystems, sind die Umkehrfunktionen nicht für alle Winkel eindeutig zurückzurechnen, hier muss man also ein wenig aufpassen, z.B. gibt arcsin(sin(ß)) im Bereich 90°-180° den Winkel 180° - ß aus. Im übrigen ist darauf zu achten, dass die FPU im Bogen- und nicht im Gradmaß rechnet. Umgerechnet werden kann wie folgt: |
[[Bild:Tutorial_Lineare_Algebra_deg2rad.png]] | [[Bild:Tutorial_Lineare_Algebra_deg2rad.png]] | ||
Für den Umgang mit Sinus und Cosinus gibt es noch ein paar spezielle Formeln, die einem Arbeit abnehmen können: | Für den Umgang mit Sinus und Cosinus gibt es noch ein paar spezielle Formeln, die einem Arbeit abnehmen können: | ||
| − | <pascal> | + | <source lang="pascal"> |
sin(-ß) = - sin(ß) | sin(-ß) = - sin(ß) | ||
cos(-ß) = cos(ß) | cos(-ß) = cos(ß) | ||
| Zeile 41: | Zeile 42: | ||
sin²(ß) + cos²(ß) = 1 | sin²(ß) + cos²(ß) = 1 | ||
| − | </ | + | </source> |
Bei Bedarf stehen weitere in jeder brauchbaren Formelsammlung, aber meist kommt man mit diesen aus. | Bei Bedarf stehen weitere in jeder brauchbaren Formelsammlung, aber meist kommt man mit diesen aus. | ||
| + | |||
| + | Wozu das? Im Kapitel über [[Matrix|Matrizen]] werden wir sehen, dass sich die drei genannten trigononmetrischen Funktionen dazu nutzen lassen, das Koordinatensystem zu drehen; außerdem kann man mithilfe der genannten Formeln sin(ß) = y und cos(ß) = x ganz einfach Kreise zeichnen. Wenn man sich dann überlegt, dass [[Kugel|Kugeln]] im Prinzip nichts anderes sind, als Kreise, die entlang der Z-Achse orthogonal (rechtwinklig zur z-Achse) gezogen werden und die Außenpunkte dieser Kreise (als Radius gezogen auf der x/z-Ebene), bei entfernter Betrachtung, selbst wieder einen Kreis (hier blau gezeichnet) beschreiben... | ||
| + | |||
| + | [[Bild:Tutorial_Nachsitzen_KreisKugel.png]] | ||
| + | |||
| + | Es gibt noch viele weitere Anwendungsmöglichkeiten, gerade die Umkehrfunktionen. So kann man mit Hilfe von Trigonometrie berechnen, um wieviel Grad ein Objekt weiter gedreht werden muss, um in eine bestimmte Richtung zu zeigen. Dreiecke sind generell auch Verdächtige beim Einsatz von Trigonometrie. | ||
==Die Welt der Matrizen== | ==Die Welt der Matrizen== | ||
| − | Matrizen gelten als das Handwerkszeugs eines 3D Programmierers. Sie sind, wenn man sie einmal verstanden hat, ein mächtiges | + | Matrizen gelten als das Handwerkszeugs eines 3D Programmierers. Sie sind, wenn man sie einmal verstanden hat, ein mächtiges Hilfsmittel, das man irgendwann nicht mehr missen mag und kann! Vorher sollten wir aber noch einmal Vertieces in OpenGl (bei D3D läuft es im Prinzip genauso) betrachten und uns erst dann auf Matrizen stürzen. |
===Vertices und ihr Ursprung=== | ===Vertices und ihr Ursprung=== | ||
| − | Ein Vertex beschreibt einen Punkt im 3D Raum. Man könnte nun annehmen, dass ein Vertex durch 3 Koordinaten x,y,z beschrieben wird. | + | Ein Vertex beschreibt einen Punkt im 3D Raum. Man könnte nun annehmen, dass ein Vertex durch 3 Koordinaten x,y,z beschrieben wird. Falsch gedacht, denn die meisten 3D APIs verwenden '''4-Dimensionale''' Vertices(x/y/z/w)?!? |
| − | Ich denke, zu den 3 ersten Koordinaten muss ich nichts weiter sagen, zur w-Koordinate hingegen schon: w ist normalerweise immer 1.0. Mit glVertex4 kann bei Bedarf auch ein anderer Wert zugewiesen werden. Ist w ungleich Null, so wird ein Vertex als folgender 3-Dimensionaler Punkt interpretiert: (x/w, y/w, z/w). Im Normalfall sollte der Wert für w aber auf 1.0 belassen werden, es sei denn man hat eine interessante Idee, die sich mit einem w ungleich 1.0 besonders schön realisieren lässt.Wen die w-Koordinate interessiert, sollte in der OpenGl Spezifikation unter Coordinate Transformations nachschauen. | + | Ich denke, zu den 3 ersten Koordinaten muss ich nichts weiter sagen, zur w-Koordinate hingegen schon: w ist normalerweise immer 1.0. Mit glVertex4 kann bei Bedarf auch ein anderer Wert zugewiesen werden. Ist w ungleich Null, so wird ein Vertex als folgender 3-Dimensionaler Punkt interpretiert: (x/w, y/w, z/w). Im Normalfall sollte der Wert für w aber auf 1.0 belassen werden, es sei denn man hat eine interessante Idee, die sich mit einem w ungleich 1.0 besonders schön realisieren lässt. Wen die w-Koordinate interessiert, sollte in der OpenGl Spezifikation unter Coordinate Transformations nachschauen. |
| − | Ein Beispiel für die | + | Ein Beispiel für die Effekt beim Einsatz von w Koordinaten: Beim ersten Dreieck ist im oberen Punkt w = 1.0, im 2. ist w = 0.5: |
[[Bild:Tutorial_Nachsitzen_wcoord.jpg]] | [[Bild:Tutorial_Nachsitzen_wcoord.jpg]] | ||
| − | |||
| − | |||
===Einstieg in Matrizen=== | ===Einstieg in Matrizen=== | ||
| Zeile 70: | Zeile 75: | ||
===Anwendung der Matrix auf einen Vektor=== | ===Anwendung der Matrix auf einen Vektor=== | ||
| − | Hat man nun ein 3-Dimensionales Vertex(w=1.0 | + | Hat man nun ein 3-Dimensionales Vertex (w=1.0) und möchte diesen durch die Matrix schicken, so rechnet man: |
[[Bild:Tutorial_Nachsitzen_Matrix4x4MulVec.png]] | [[Bild:Tutorial_Nachsitzen_Matrix4x4MulVec.png]] | ||
Bzw: | Bzw: | ||
| − | <pascal> | + | <source lang="pascal"> |
| − | x_neu := x*a[1,1] + y*a[1,2] + z*a[1,3] + a[1,4] | + | x_neu := x*a[1,1] + y*a[1,2] + z*a[1,3] + w*a[1,4] |
{Koeffizienten aus der ersten Zeile der Matrix} | {Koeffizienten aus der ersten Zeile der Matrix} | ||
| − | y_neu := x*a[2,1] + y*a[2,2] + z*a[2,3] + a[2,4] | + | y_neu := x*a[2,1] + y*a[2,2] + z*a[2,3] + w*a[2,4] |
{Koeffizienten aus der zweiten Zeile der Matrix} | {Koeffizienten aus der zweiten Zeile der Matrix} | ||
| − | z_neu := x*a[3,1] + y*a[3,2] + z*a[3,3] + a[3,4] | + | z_neu := x*a[3,1] + y*a[3,2] + z*a[3,3] + w*a[3,4] |
{Koeffizienten aus der dritten Zeile der Matrix} | {Koeffizienten aus der dritten Zeile der Matrix} | ||
| − | </ | + | w_neu := x*a[4,1] + y*a[4,2] + z*a[4,3] + w*a[4,4] |
| + | {Koeffizienten aus der letzten Zeile der Matrix} | ||
| + | </source> | ||
Wer nun ein Wenig darüber nachdenkt, kommt auf ein Ergebnis: | Wer nun ein Wenig darüber nachdenkt, kommt auf ein Ergebnis: | ||
:'''Die Spalten sind die Bilder der Einheitsvektoren''' | :'''Die Spalten sind die Bilder der Einheitsvektoren''' | ||
| − | Die Bedeutung dürfte noch | + | Die Bedeutung dürfte noch nicht klar sein, aber das kommt bald. |
| + | |||
| + | Ist (wie fast immer) w=1, dann beschreibt die letzte Spalte der Matrix eine Verschiebung der Punkte, denn in der obigen Gleichung steht dann | ||
| + | <source lang="pascal"> | ||
| + | x_neu := ... + a[1,4] | ||
| + | y_neu := ... + a[2,4] | ||
| + | z_neu := ... + a[3,4] | ||
| + | w_neu := ... + a[4,4] | ||
| + | </source> | ||
| + | Es wird dadurch die letzte Spalte auf das Vertex aufaddiert. Für alle hier genannten Matrixoperatoren gilt außerdem, dass a[4,1] = a[4,2] = a[4,3] = 0. Und für a[4,4] und w_neu: | ||
| + | <source lang="pascal"> | ||
| + | w_neu = a[4,4] = 1. | ||
| + | </source> | ||
| + | Klar ist also, dass die w-Koordinate unverändert bleibt - nur Projektionsmatrizen halten sich nicht an diese Regel, aber da liegt genau deren Trick. | ||
===Die Identitätsmatrix, oder der Ursprung von glLoadIdentity=== | ===Die Identitätsmatrix, oder der Ursprung von glLoadIdentity=== | ||
Eine der wichtigsten Matrizen ist die, die nichts macht. Also ein Vertex dorthin Projeziert, wo es sich bereits am Anfang befand: | Eine der wichtigsten Matrizen ist die, die nichts macht. Also ein Vertex dorthin Projeziert, wo es sich bereits am Anfang befand: | ||
| − | <pascal> | + | <source lang="pascal"> |
| − | V | + | Matrix * V = V |
| − | </ | + | </source> |
Schauen wir zurück, wie eine Matrix auf ein Vertex angewendet wird: | Schauen wir zurück, wie eine Matrix auf ein Vertex angewendet wird: | ||
| − | <pascal> | + | <source lang="pascal"> |
| − | x_neu := x*a[1,1] + y*a[1,2] + z*a[1,3] + a[1,4] | + | x_neu := x*a[1,1] + y*a[1,2] + z*a[1,3] + w*a[1,4] |
| − | </ | + | </source> |
Unser Ziel ist, dass x_neu gleich x ist. Das lässt sich immer erreichen, indem wir den Koeffizienten a[1,1] = 1.0 setzen und die restichen = 0. Dann steht da nämlich: | Unser Ziel ist, dass x_neu gleich x ist. Das lässt sich immer erreichen, indem wir den Koeffizienten a[1,1] = 1.0 setzen und die restichen = 0. Dann steht da nämlich: | ||
| − | <pascal> | + | <source lang="pascal"> |
| − | x_neu := x*1 + y*0 + z*0 + 0 { = x } | + | x_neu := x*1 + y*0 + z*0 + w*0 { = x } |
| − | </ | + | </source> |
| − | Die gleiche Überlegung kann man auch für die | + | Die gleiche Überlegung kann man auch für die Anderen 3 Elemente y,z und w machen. Jede dieser Überlegungen ergibt eine Zeile der Identitätsmatrix. Das Ergebnis: |
[[Bild:Tutorial_Nachsitzen_IdentityMatrix.png]] | [[Bild:Tutorial_Nachsitzen_IdentityMatrix.png]] | ||
| Zeile 110: | Zeile 130: | ||
===Welten verschieben=== | ===Welten verschieben=== | ||
| − | Überlebenswichtig in 3D Anwendungen dürften die Translationsmatrizen sein, die ein Vertex verschieben | + | Überlebenswichtig in 3D Anwendungen dürften die Translationsmatrizen sein, die ein Vertex verschieben - aber das haben wir ja schon ein paar Zeilen weiter oben geklärt, wie man das durch w=1 und der letzten Spalte der Matrix anstellt. |
[[Bild:Tutorial_Nachsitzen_MoveMatrix.png]] | [[Bild:Tutorial_Nachsitzen_MoveMatrix.png]] | ||
| Zeile 116: | Zeile 136: | ||
===Um den Ursprung drehen=== | ===Um den Ursprung drehen=== | ||
| − | Ein Porsche, den man vor zurück, links, rechts hoch und runterbewegen kann, ist schon was tolles. | + | Ein Porsche, den man vor zurück, links, rechts hoch und runterbewegen kann, ist schon was tolles. Deutlich mehr Klasse bekommt er, wenn man ihn auch noch aus verschiedenen Blickwinkeln anschauen und frei drehen kann. Den meisten dürfte damit schon klar sein, worauf ich hinaus will: Drehungen: |
| + | |||
| + | {| border="1" | ||
| + | |- valign="top" | ||
| + | | [[Bild:Tutorial_Nachsitzen_rotz.gif]] | ||
| + | | | ||
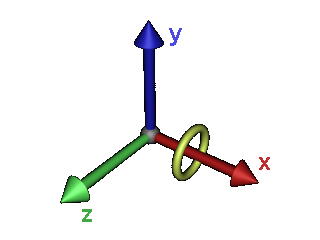
====Drehen um die Z-Achse==== | ====Drehen um die Z-Achse==== | ||
| − | + | Rotationen zusammenstöpseln geht einfach. Erinnern wir uns an den Satz: "Die Spalten sind die Bilder der Einheitsvektoren". Mit dieser Hilfe können wir uns jetzt selbst überlegen, wie eine Rotationsmatrix, die um die Z-Achse mit dem Winkel ß dreht, auszusehen hat. | |
| − | |||
| − | Rotationen zusammenstöpseln geht | ||
Gehen wir die Einheitsvektoren der Reihe nach ab: | Gehen wir die Einheitsvektoren der Reihe nach ab: | ||
| − | Der Z-Achsen Einheitsvektor(0.0, 0.0, 1.0) bleibt bei unserer Rotation unverändert - man nehme einen Finger, deute damit nach vorne. Nun drehe man diesen Finger um seine eigene Achse, wohin zeigt er? In die selbe Richtung | + | Der Z-Achsen Einheitsvektor(0.0, 0.0, 1.0) bleibt bei unserer Rotation unverändert - man nehme einen Finger, deute damit nach vorne. Nun drehe man diesen Finger um seine eigene Achse, wohin zeigt er? In die selbe Richtung wie vor der Drehung? So sollte es zumindest sein, ansonsten habt ihr ein anatomisches Problem ;-). Damit entspricht Z-Achsen Einheitsvektor auch der vorletzen Spalte der Matrix: (0.0, 0.0, 1.0, 0.0) |
| − | Der X-Achsen Einheitsvektor(1.0, 0.0, 0.0) | + | Der X-Achsen Einheitsvektor(1.0, 0.0, 0.0) dreht sich hingegen mit. Trigonometrie findet der Lösung Spur. Ein Blick auf das Bild zum Einheitskreis zeigt, dass wir gerade das gleiche Problem für X und Y zu bewältigen haben: Die Rotationsachse ist in beiden Fällen die Z-Achse. Der Einheitsvektor, der gedreht wird, ist der X-Achsen Einheitsvektor also: |
| − | <pascal> | + | <source lang="pascal"> |
x := cos(ß) | x := cos(ß) | ||
y := sin(ß) | y := sin(ß) | ||
| − | </ | + | </source> |
womit wir den Inhalt der ersten Spalte der Matrix kennen: (cos(ß); sin(ß); 0; 0) | womit wir den Inhalt der ersten Spalte der Matrix kennen: (cos(ß); sin(ß); 0; 0) | ||
Das lässt sich jetzt genauso auf den Y-Achsen Einheitsvektor(0.0, 1.0, 0.0) übertragen, man muss nur bedenken in welcher weise sich x und y vertauschen: | Das lässt sich jetzt genauso auf den Y-Achsen Einheitsvektor(0.0, 1.0, 0.0) übertragen, man muss nur bedenken in welcher weise sich x und y vertauschen: | ||
| − | <pascal> | + | <source lang="pascal"> |
x = -sin(ß) | x = -sin(ß) | ||
y = cos(ß) | y = cos(ß) | ||
| − | </ | + | </source> |
So ergibt sich für die zweite Spalte: (-sin(ß); cos(ß); 0; 0) | So ergibt sich für die zweite Spalte: (-sin(ß); cos(ß); 0; 0) | ||
| Zeile 144: | Zeile 167: | ||
[[Bild:Tutorial_Nachsitzen_RotZMatrix.png]] | [[Bild:Tutorial_Nachsitzen_RotZMatrix.png]] | ||
| + | |- valign="top" | ||
| + | | [[Bild:Tutorial_Nachsitzen_roty.gif]] | ||
| + | | | ||
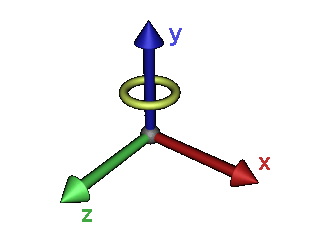
| + | ====Drehen um die Y-Achse==== | ||
| + | |||
| + | Wenn man nun auf die gleiche Weise an die weiteren Drehachsen herangeht, so wird man auf dieses Ergebnis kommen: | ||
| + | |||
| + | [[Bild:Tutorial_Nachsitzen_RotYMatrix.png]] | ||
| + | |- valign="top" | ||
| + | | [[Bild:Tutorial_Nachsitzen_rotx.gif]] | ||
| + | | | ||
====Drehen um die X-Achse==== | ====Drehen um die X-Achse==== | ||
| − | + | [[Bild:Tutorial_Nachsitzen_RotXMatrix.png]] | |
| + | |} | ||
| + | |||
| + | ===Matrixoperationen=== | ||
| + | |||
| + | Fürs Arbeiten mit Matrizen gibt es ein paar wichtige Operationen. Ohne diese macht das Arbeiten wenig Spaß und würde einem auch wenig bringen. | ||
| + | |||
| + | Ich möchte hier keine genaue Erläuterung über die Funktionsweise dieser Operationen geben, aber erklären, was sie tun und was man damit anstellen kann. Wer diese Operationen verwenden möchte, sollte mal auf Mike Lischkes Homepage vorbeischaun. Dort findet ihr eine Geometry.pas, die diese Funktionen und noch viele mehr beinhaltet. Eine etwas verbesserte und immer wieder aktualisierte Variante liegt dem glScene Projekt bei. Mathematische Details findet ihr in unseren Wiki-Artikeln [[Matrix]] und [[Techniken_zur_Matrixinversion]]. | ||
| + | |||
| + | ===Matrixmultiplikation=== | ||
| + | |||
| + | Eine wichtige Operation ist die Matrixmultiplikation. Sie verbindet zwei Matrizen zu einer so, dass sie nacheinander ausgeführt werden. Dabei ist zu bedenken, dass die Reihenfolge einen Unterschied macht: erst drehen und dann verschieben ist ungleich erst verschieben und dann drehen, aber das solltet ihr bei der Verwendung von glRotate und glTranslate längst bemerkt haben. | ||
| + | |||
| + | Nun wie multipliziert man Matrizen miteinander? Wie wollen M mit M' multiplizieren. Die Spalten von M' kann man als Vektoren auffassen. Also wendet man einfach M auf die Spalten von M' und bekommt dabei 4 Vektoren. Diese setzt man wieder in einer neuen Matrix nebeneinander und schon hat man M mit M' multipliziert. Ausführlicher wie gesagt im [[Matrix]] Artikel. | ||
| + | |||
| + | ===Matrixinversion=== | ||
| + | |||
| + | Eine invertierte Matrix macht genau das Gegenteil der ursprünglichen Matrix. Verschiebt die ursprüngliche ein Vertex um 3 nach rechts, so schiebt die intervtierte Matrix ein Vertex um 3 nach links (Achtung: nicht alle Matrizen sind invertierbar, Rotations- und Translationsmatrizen lassen sich jedoch immer invertieren). Dies lässt sich sinnvoll bei Kameras einsetzen: | ||
| + | |||
| + | Man hat ein Objekt, dessen Rotation durch eine Matrix beschrieben wird, was generell sinnvoll ist, wenn das Objekt voneinander abhängige Drehungen vollführen soll oder man das lokale Koordinatensystem des Objekts benötigt. Jedenfalls will man nun das Objekt nicht von außen bestaunen, sondern sich in die Ansicht des Objekts selbst hineinversetzen, so kann man dessen Rotationsmatrix einfach invertieren und schon hat man sein Ziel erreicht. Wen ähnliches interessiert, sollte sich jetzt einmal an mein [[Tutorial_Kamera1|Kamera Tutorial]] wagen und schauen, dass er's versteht. | ||
| + | |||
| + | Für allgemeine Matrizen ist die nötige Rechnerei leider nicht ganz harmlos. Ich empfehle hierzu einen Blick in die Wikipedia unter Inverse Matrix oder bessere Matheformelsammlungen bzw. Geometrie oder Lineare Algebra Skripte. Ist die Matrix dagegen ein Produkt aus Verschiebungen und Rotationen, dann langt bereits der Artikel [[Techniken_zur_Matrixinversion]]. | ||
| + | |||
| + | ==OpenGl, Direct3D, IrixGl, MesaGl,... und das Thema Matrizen== | ||
| + | |||
| + | Wie hat man sich gefreut, als man glaubt Matrizen endlich ein wenig verstanden zu haben und dann das! Die ersten Versuche mit [[glLoadMatrix]] und [[glMultMatrix]] müssen zwingend schiefgehen. Immer, wenn man nicht vorgewarnt wird. Wer glaubt seine Matrizen einfach mit einem 2 Dimensionalen Array beschreiben zu können irrt. Die Idee ist zwar nicht schlecht, aber aus Performancegründen liegen die OpenGl Matrizen nicht zeilenweise, sondern spaltenweise im Speicher: | ||
| + | |||
| + | [[Bild:Tutorial_Nachsitzen_GlMatrix.png]] | ||
| + | |||
| + | Ich persönlich bevorzuge meist, statt dass ich in einem 2D-Array immer mit den Zugriffsvariablen herumwurschtle, den Zugriff auf die Matrix mit einem eindimensionalen Array. Die obige Tabelle hilft, die passene Zelle zu finden. | ||
| + | |||
| + | ==Kopfschmerzen?== | ||
| + | |||
| + | Ahh, wieder eines meiner schrecklichen Tutorials überlebt. Ich hoffe, dass wenigstens ein paar Leute unter euch das ein oder andere Verstanden haben und ich das alles nicht umsonst geschrieben habe (wenns nur einer Verstanden hat, bin ich schon glücklich ;-) ). Ein paar weitere, spannende Hilfsmittel, die hier nicht unerwähnt bleiben sollten, sind das [[Standard_Skalarprodukt|Punktprodukt]] und das [[Vektorprodukt]], welche Hilfsmittel in der Vektorrechung sind. Defizite dort gleicht das Tutorial über [[Tutorial_Lineare_Algebra|Lineare Algebra]] aus. | ||
| + | ...have a lot of fun! | ||
| − | + | Delphic | |
| − | |||
| + | {{TUTORIAL_NAVIGATION| [[Tutorial Lineare Algebra]] | [[Tutorial Objekt gedreht und dennoch nach vorne bewegt]]}} | ||
| − | [[ | + | [[Kategorie:Tutorial|Nachsitzen]] |
Aktuelle Version vom 25. September 2013, 15:30 Uhr
Inhaltsverzeichnis
- 1 Vorwort
- 2 Trigonometrie am rechtwinkligen Dreieck
- 3 Die Welt der Matrizen
- 4 OpenGl, Direct3D, IrixGl, MesaGl,... und das Thema Matrizen
- 5 Kopfschmerzen?
Vorwort
Immer wieder muss ich feststellen, dass viele, die (mit OpenGl) 3D Anwendungen schreiben, nichts mit der Mathematik dahinter anfangen können. Um das Ein oder Andere zu verstehen oder sich selbst überlegen zu können, ist dieses Wissen aber unabdingbar. Ich möchte mit diesem Artikel helfen, diesen Zustand zu beenden und entsprechends Wissen unter euch verbreiten. Dies und das werded ihr aus der Schule kennen, wenn ihr also etwas überspringen wollt, orientiert euch an den Überschriften.
Trigonometrie am rechtwinkligen Dreieck
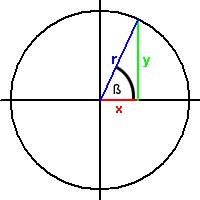
Man stelle sich vor, man hat einen Kreis, mit Radius 1. Der Mittelpunkt des Kreises befindet sich auf dem Koordinatensystem Ursprung. An der X-Achse ist ein Winkel ß angetragen:
An der x-Achse bildet sich dann ein rechter Winkel (wichtig für normale Trigonometrie). Die diesem Winkel gegenüberliegende Seite(r) nennt man Hypotenuse. Die am Winkel ß anliegende Seite(x) ist die Ankathete. Die dem Winkel gegenüberliegende Seite(y) heißt Gegenkathete. Man definiert folgende Funktionen:
sin(ß) = Gegenkathete / Hypotenuse
cos(ß) = Ankathete / Hypotenuse
tan(ß) = Gegenkathete / Ankathete
Im Einheitskreis(und nur dort) gilt:
sin(ß) = y
cos(ß) = x
da die Länge der Hypotenuse 1 ist(Kreisradius).
Die Umkehrfunktionen dazu sind (in Pascal):
ß = arcsin(sin(ß))
ß = arccos(cos(ß))
ß = arctan(tan(ß))
für ß im Bereich 0° - 90°. In den anderen Quadranten des Koordinatensystems, sind die Umkehrfunktionen nicht für alle Winkel eindeutig zurückzurechnen, hier muss man also ein wenig aufpassen, z.B. gibt arcsin(sin(ß)) im Bereich 90°-180° den Winkel 180° - ß aus. Im übrigen ist darauf zu achten, dass die FPU im Bogen- und nicht im Gradmaß rechnet. Umgerechnet werden kann wie folgt:
Für den Umgang mit Sinus und Cosinus gibt es noch ein paar spezielle Formeln, die einem Arbeit abnehmen können:
sin(-ß) = - sin(ß)
cos(-ß) = cos(ß)
sin(90° - ß) = cos (ß)
cos(90° - ß) = sin (ß)
sin²(ß) + cos²(ß) = 1
Bei Bedarf stehen weitere in jeder brauchbaren Formelsammlung, aber meist kommt man mit diesen aus.
Wozu das? Im Kapitel über Matrizen werden wir sehen, dass sich die drei genannten trigononmetrischen Funktionen dazu nutzen lassen, das Koordinatensystem zu drehen; außerdem kann man mithilfe der genannten Formeln sin(ß) = y und cos(ß) = x ganz einfach Kreise zeichnen. Wenn man sich dann überlegt, dass Kugeln im Prinzip nichts anderes sind, als Kreise, die entlang der Z-Achse orthogonal (rechtwinklig zur z-Achse) gezogen werden und die Außenpunkte dieser Kreise (als Radius gezogen auf der x/z-Ebene), bei entfernter Betrachtung, selbst wieder einen Kreis (hier blau gezeichnet) beschreiben...
Es gibt noch viele weitere Anwendungsmöglichkeiten, gerade die Umkehrfunktionen. So kann man mit Hilfe von Trigonometrie berechnen, um wieviel Grad ein Objekt weiter gedreht werden muss, um in eine bestimmte Richtung zu zeigen. Dreiecke sind generell auch Verdächtige beim Einsatz von Trigonometrie.
Die Welt der Matrizen
Matrizen gelten als das Handwerkszeugs eines 3D Programmierers. Sie sind, wenn man sie einmal verstanden hat, ein mächtiges Hilfsmittel, das man irgendwann nicht mehr missen mag und kann! Vorher sollten wir aber noch einmal Vertieces in OpenGl (bei D3D läuft es im Prinzip genauso) betrachten und uns erst dann auf Matrizen stürzen.
Vertices und ihr Ursprung
Ein Vertex beschreibt einen Punkt im 3D Raum. Man könnte nun annehmen, dass ein Vertex durch 3 Koordinaten x,y,z beschrieben wird. Falsch gedacht, denn die meisten 3D APIs verwenden 4-Dimensionale Vertices(x/y/z/w)?!?
Ich denke, zu den 3 ersten Koordinaten muss ich nichts weiter sagen, zur w-Koordinate hingegen schon: w ist normalerweise immer 1.0. Mit glVertex4 kann bei Bedarf auch ein anderer Wert zugewiesen werden. Ist w ungleich Null, so wird ein Vertex als folgender 3-Dimensionaler Punkt interpretiert: (x/w, y/w, z/w). Im Normalfall sollte der Wert für w aber auf 1.0 belassen werden, es sei denn man hat eine interessante Idee, die sich mit einem w ungleich 1.0 besonders schön realisieren lässt. Wen die w-Koordinate interessiert, sollte in der OpenGl Spezifikation unter Coordinate Transformations nachschauen.
Ein Beispiel für die Effekt beim Einsatz von w Koordinaten: Beim ersten Dreieck ist im oberen Punkt w = 1.0, im 2. ist w = 0.5:
Einstieg in Matrizen
Beginnen wir am Anfang mit einer allgemeinen Definition einer Matrix:
Definition:Eine m x n Matrix ist eine Tabelle aus Werten mit n Spalten und m Zeilen.
Die in Direct3D und OpenGl Verwendung findenen Matrizen sind generell 4x4 Matrizen, mit Singles als Elemente:
Anwendung der Matrix auf einen Vektor
Hat man nun ein 3-Dimensionales Vertex (w=1.0) und möchte diesen durch die Matrix schicken, so rechnet man:
Bzw:
x_neu := x*a[1,1] + y*a[1,2] + z*a[1,3] + w*a[1,4]
{Koeffizienten aus der ersten Zeile der Matrix}
y_neu := x*a[2,1] + y*a[2,2] + z*a[2,3] + w*a[2,4]
{Koeffizienten aus der zweiten Zeile der Matrix}
z_neu := x*a[3,1] + y*a[3,2] + z*a[3,3] + w*a[3,4]
{Koeffizienten aus der dritten Zeile der Matrix}
w_neu := x*a[4,1] + y*a[4,2] + z*a[4,3] + w*a[4,4]
{Koeffizienten aus der letzten Zeile der Matrix}
Wer nun ein Wenig darüber nachdenkt, kommt auf ein Ergebnis:
- Die Spalten sind die Bilder der Einheitsvektoren
Die Bedeutung dürfte noch nicht klar sein, aber das kommt bald.
Ist (wie fast immer) w=1, dann beschreibt die letzte Spalte der Matrix eine Verschiebung der Punkte, denn in der obigen Gleichung steht dann
x_neu := ... + a[1,4]
y_neu := ... + a[2,4]
z_neu := ... + a[3,4]
w_neu := ... + a[4,4]
Es wird dadurch die letzte Spalte auf das Vertex aufaddiert. Für alle hier genannten Matrixoperatoren gilt außerdem, dass a[4,1] = a[4,2] = a[4,3] = 0. Und für a[4,4] und w_neu:
w_neu = a[4,4] = 1.
Klar ist also, dass die w-Koordinate unverändert bleibt - nur Projektionsmatrizen halten sich nicht an diese Regel, aber da liegt genau deren Trick.
Die Identitätsmatrix, oder der Ursprung von glLoadIdentity
Eine der wichtigsten Matrizen ist die, die nichts macht. Also ein Vertex dorthin Projeziert, wo es sich bereits am Anfang befand:
Matrix * V = V
Schauen wir zurück, wie eine Matrix auf ein Vertex angewendet wird:
x_neu := x*a[1,1] + y*a[1,2] + z*a[1,3] + w*a[1,4]
Unser Ziel ist, dass x_neu gleich x ist. Das lässt sich immer erreichen, indem wir den Koeffizienten a[1,1] = 1.0 setzen und die restichen = 0. Dann steht da nämlich:
x_neu := x*1 + y*0 + z*0 + w*0 { = x }
Die gleiche Überlegung kann man auch für die Anderen 3 Elemente y,z und w machen. Jede dieser Überlegungen ergibt eine Zeile der Identitätsmatrix. Das Ergebnis:
Ausgehend von dieser Matrix kann man sich jetzt weitere Matrizen überlegen:
Welten verschieben
Überlebenswichtig in 3D Anwendungen dürften die Translationsmatrizen sein, die ein Vertex verschieben - aber das haben wir ja schon ein paar Zeilen weiter oben geklärt, wie man das durch w=1 und der letzten Spalte der Matrix anstellt.
Um den Ursprung drehen
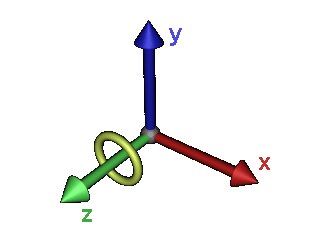
Ein Porsche, den man vor zurück, links, rechts hoch und runterbewegen kann, ist schon was tolles. Deutlich mehr Klasse bekommt er, wenn man ihn auch noch aus verschiedenen Blickwinkeln anschauen und frei drehen kann. Den meisten dürfte damit schon klar sein, worauf ich hinaus will: Drehungen:
Matrixoperationen
Fürs Arbeiten mit Matrizen gibt es ein paar wichtige Operationen. Ohne diese macht das Arbeiten wenig Spaß und würde einem auch wenig bringen.
Ich möchte hier keine genaue Erläuterung über die Funktionsweise dieser Operationen geben, aber erklären, was sie tun und was man damit anstellen kann. Wer diese Operationen verwenden möchte, sollte mal auf Mike Lischkes Homepage vorbeischaun. Dort findet ihr eine Geometry.pas, die diese Funktionen und noch viele mehr beinhaltet. Eine etwas verbesserte und immer wieder aktualisierte Variante liegt dem glScene Projekt bei. Mathematische Details findet ihr in unseren Wiki-Artikeln Matrix und Techniken_zur_Matrixinversion.
Matrixmultiplikation
Eine wichtige Operation ist die Matrixmultiplikation. Sie verbindet zwei Matrizen zu einer so, dass sie nacheinander ausgeführt werden. Dabei ist zu bedenken, dass die Reihenfolge einen Unterschied macht: erst drehen und dann verschieben ist ungleich erst verschieben und dann drehen, aber das solltet ihr bei der Verwendung von glRotate und glTranslate längst bemerkt haben.
Nun wie multipliziert man Matrizen miteinander? Wie wollen M mit M' multiplizieren. Die Spalten von M' kann man als Vektoren auffassen. Also wendet man einfach M auf die Spalten von M' und bekommt dabei 4 Vektoren. Diese setzt man wieder in einer neuen Matrix nebeneinander und schon hat man M mit M' multipliziert. Ausführlicher wie gesagt im Matrix Artikel.
Matrixinversion
Eine invertierte Matrix macht genau das Gegenteil der ursprünglichen Matrix. Verschiebt die ursprüngliche ein Vertex um 3 nach rechts, so schiebt die intervtierte Matrix ein Vertex um 3 nach links (Achtung: nicht alle Matrizen sind invertierbar, Rotations- und Translationsmatrizen lassen sich jedoch immer invertieren). Dies lässt sich sinnvoll bei Kameras einsetzen:
Man hat ein Objekt, dessen Rotation durch eine Matrix beschrieben wird, was generell sinnvoll ist, wenn das Objekt voneinander abhängige Drehungen vollführen soll oder man das lokale Koordinatensystem des Objekts benötigt. Jedenfalls will man nun das Objekt nicht von außen bestaunen, sondern sich in die Ansicht des Objekts selbst hineinversetzen, so kann man dessen Rotationsmatrix einfach invertieren und schon hat man sein Ziel erreicht. Wen ähnliches interessiert, sollte sich jetzt einmal an mein Kamera Tutorial wagen und schauen, dass er's versteht.
Für allgemeine Matrizen ist die nötige Rechnerei leider nicht ganz harmlos. Ich empfehle hierzu einen Blick in die Wikipedia unter Inverse Matrix oder bessere Matheformelsammlungen bzw. Geometrie oder Lineare Algebra Skripte. Ist die Matrix dagegen ein Produkt aus Verschiebungen und Rotationen, dann langt bereits der Artikel Techniken_zur_Matrixinversion.
OpenGl, Direct3D, IrixGl, MesaGl,... und das Thema Matrizen
Wie hat man sich gefreut, als man glaubt Matrizen endlich ein wenig verstanden zu haben und dann das! Die ersten Versuche mit glLoadMatrix und glMultMatrix müssen zwingend schiefgehen. Immer, wenn man nicht vorgewarnt wird. Wer glaubt seine Matrizen einfach mit einem 2 Dimensionalen Array beschreiben zu können irrt. Die Idee ist zwar nicht schlecht, aber aus Performancegründen liegen die OpenGl Matrizen nicht zeilenweise, sondern spaltenweise im Speicher:
Ich persönlich bevorzuge meist, statt dass ich in einem 2D-Array immer mit den Zugriffsvariablen herumwurschtle, den Zugriff auf die Matrix mit einem eindimensionalen Array. Die obige Tabelle hilft, die passene Zelle zu finden.
Kopfschmerzen?
Ahh, wieder eines meiner schrecklichen Tutorials überlebt. Ich hoffe, dass wenigstens ein paar Leute unter euch das ein oder andere Verstanden haben und ich das alles nicht umsonst geschrieben habe (wenns nur einer Verstanden hat, bin ich schon glücklich ;-) ). Ein paar weitere, spannende Hilfsmittel, die hier nicht unerwähnt bleiben sollten, sind das Punktprodukt und das Vektorprodukt, welche Hilfsmittel in der Vektorrechung sind. Defizite dort gleicht das Tutorial über Lineare Algebra aus.
...have a lot of fun!
Delphic
|
|
||
Vorhergehendes Tutorial: Tutorial Lineare Algebra |
Nächstes Tutorial: Tutorial Objekt gedreht und dennoch nach vorne bewegt |
|
|
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen. |
||