Tutorial Objekt gedreht und dennoch nach vorne bewegt
Inhaltsverzeichnis
Vorwort
Beim Erstellen eines 3D-Games steht man irgendwann vor einem gewaltigen Problem: Ich kann zwar mein Objekt drehen und Transformieren, aber was mache ich, wenn sich das Objekt an der aktuellen Position um z.B. 15 Grad drehen und trotzdem in seine Blick-Richtung bewegen soll?!?
Die Lösung des Problems heißt: Look-Vektor!!! Look was?!? Keine Panik, ich werd's euch erklären.
Der Richtungs-Vektor
Um ein Objekt immer nach vorne bewegen zu können, muss ich wissen, wo momentan für das Objekt vorne ist. Dazu benötige ich den Richtungs-Vektor (ich nenne ihn mal Look-Vektor) Bei einer Drehung des Objektes, wird der Vektor mitgedreht und zeigt somit immer nach vorn. Klingt komisch, ist aber so :o) Nein, im ernst: Es ist eigentlich kein Problem wie ihr sehen werdet.
Bevor wir anfangen...
...gibt es noch ein paar Kleinigkeiten zu regeln.
- um ein Objekt wie z.B. einen Raumgleiter in einer entsprechenden Simulation zu bewegen, müssen 3 Lokale Vektoren mitverwendet werden, welche ein lokales Koordinatensystem darstellen. Mit diesem Lokalen Koordinatensystem muss dann bei Drehungen gearbeitet werden. Das kommt aber in ein anderes Tutorial. Hier wird das ganze nur mit einem Vektor gemacht, was für den Anfang das Prinzip hinter der ganzen Geschichte verdeutlichen soll.
- Um die Vektor-Rotation durchführen zu können, verwende ich die Geometry.pas von GLScene. Bei dieser Datei handelt es sich um eine Ansammlung ziemlich nützlicher mathematischer Prozeduren welche teilweise sogar für 3Dnow ™ optimiert sind. Ursprünglich (ohne Optimierung für 3Dnow ™) kommt diese Unit von Mike Lischke.
- Ich gehe davon aus, dass ihr bereits wisst, wie ein Objekt mit Hilfe von glRotate gedreht, glTranslate positioniert und Objekte mit den entsprechenden Funktionen darstellt. Solltet ihr über dieses Wissen nicht verfügen, schaut euch die anderen Tutorials an. (z.B. Tutorial Matrix2)
- Ihr wisst bescheid, was ein Vektor ist und was er macht. Wenn nicht: ein Vektor ist ein Pfeil von Punkt A auf Punkt B. Wenn A der 0-Punkt des globalen Koordinatensystems ist (und damit der Ursprung jedes Nullvektors) und B die Position eures Objektes im 3D-Raum, dann wird der Vektor von Punkt A nach Punkt B auch Nullvektor genannt. Ok, das war der Vektor in Grob-Form.
- Das Ganze baut auf das API-Tutorial 2 auf. Es wurden eigentlich nur die Funktionen glDraw und ProcessKeys geändert.
Und los gehts
Da wir unser Objekt Rotieren, benötigen wir erst einmal die Variablen um die Rotation der entsprechenden Achse zu merken, sowie den Vektor welcher die Position unseres Objektes beinhaltet. Dieser ist in der Geometry.pas deklariert:
var
RotateX : single; // Rotation um die X-Achse
RotateY : single; // Rotation um die Y-Achse
RotateZ : single; // Rotation um die Z-Achse
PosVect : TVector3f; // Vector mit der Position des Objektes.
Diese Variablen werden in der WndProc mit den Standard-Werten initialisiert. Dabei wird für den Positions-Vektor der Z Wert auf -5 gesetzt (um hinter das Near Clipping Plane zu kommen), damit das Objekt überhaupt erstmal sichtbar ist.
RotateX := 0;
RotateY := 0;
RotateZ := 0;
PosVect[0] := 0;
PosVect[1] := 0;
PosVect[2] := -5;
So, nun kommen wir zu glDraw. Auch hier läuft alles nach dem alt bekannten System ab. Bildschirm und Z-Buffer löschen, Objekt positionieren, rotieren und dann zeichnen. Letzteres wurde von mir in die Prozedur DrawTheObject ausgelagert, um die glDraw nicht ganz so unübersichtlich zu gestallten. Es gibt eigentlich nur zwei Erweiterungen zum Tutorial 2.
Die erste: Das Objekt wird um die X, Y und Z Achse gedreht wird, je nach Wert der Rotations-Variablen. Dabei ist die Reichenfolge von Zuerst X, Y, Z einzuhalten, da es sonst zu unerwünschten Resultaten kommt. (Echt witzig. Probiert's mal aus ;o) ). Die zweite: für Translate werden nun nicht mehr Fix-Werte verwendet, sondern die aktuellen Werte des Vektors welcher die aktuelle Position des Objektes beinhaltet.
glClearColor(0,0,0,0);
glClear(GL_COLOR_BUFFER_BIT or GL_DEPTH_BUFFER_BIT);
glLoadIdentity;
// Das Objekt auf seine aktuelle Position setzen.
glTranslate( PosVect[0], PosVect[1], PosVect[2]);
{ Das Objekt noch drehen, damit denn wir haben bis jetzt ja nur den }
{ Vector gedreht. }
glRotate(RotateX, 1, 0, 0);
glRotate(RotateY, 0, 1, 0);
glRotate(RotateZ, 0, 0, 1);
DrawTheObject;
Die Prozedur DrawTheObject muss hier nicht weiter aufgelistet werden, da dort nur die (ständig unveränderten) Objekt-Daten an OpenGL weitergeleitet werden. Bis jetzt nichts außergewöhnliches, oder ?!?
Die Tasten-Verarbeitung
ProcessKey wurde ebenfalls ein kleinwenig angepasst. Hier werden die Tasten R (für Reset), W, S, A, D, Links, Rechts, Oben und Unten abgefragt und entsprechend reagiert. Dabei wird mit W und S das Objekt in der X-Achse gedreht, mit A und D in der Y Achse und mit Rechts und Links in der Z Achse. R setzt alles Werte wieder auf den Standard zurück. Ich führe hier nur als Beispiel die Abfrage für die X Achse an. R ist selbsterklärend und auf Oben und Unten gehe ich später noch genauer ein.
Eigentlich wird hier nichts besonderes gemacht: Die Variable mit den Rotations-Daten werden entsprechend der gedrückten Taste angepasst. Sollte der Winkel 360 Grad über- oder 0 Grad unterschreiten, wird entsprechend zurückgesetzt, damit ein Drehwinkel von 0 - 360 Grad eingehalten wird. Ich habe übrigens für jede Rotation eine eigene Prozedur geschrieben um das ganze etwas übersichtlicher zu halten:
// Überprüfen, ob W gedrückt wurde (Drehung um X-Achse)
if Keys[ord('W')] then
begin
//--- Die Rotation um die X-Achse erhöhen. ---------------------------------
RotateX := RotateX + 0.8;
//--- Sollte RotateX größer als 360 Grad sein, den Wert umrechnen. Dadurch
// wird der Drehungs-Bereich auf 0 - 360 Grad begrenzt.
if RotateX > 360 then RotateX := RotateX - 360;
end;
// Überprüfen, ob W gedrückt wurde (Drehung um X-Achse)
if Keys[ord('S')] then
begin
//--- Die Rotation um die X-Achse erniedrigen. -----------------------------
RotateX := RotateX - 0.8;
//--- Sollte RotateX kleiner als 0 Grad sein, den Wert umrechnen. Dadurch
// wird der Drehungs-Bereich auf 0 - 360 Grad begrenzt.
if RotateX <= 0 then RotateX := RotateX + 360;
end;
Ich denke, mit Hilfe der Kommentare dürften alle übriggebliebenen Fragen geklärt sein (scheint so, als wäre ich Optimist *grins*). Wenn euch die Rotation zu langsam ist, verwendet einfach an Stelle von 0.8 einen anderen Wert. Je größer, um so schneller ist die Rotation.
Das ganze ist ein auf und ab...
Ich hab's euch versprochen: auf die Oben und Unten-Taste gehe ich genauer ein. Der Grund ist ganz einfach: hier spielt sich der eigentliche Vektor-Rotations-Vorgang ab. Hier liegt das Geheimnis. Aber keine Angst, ich gehe, wie versprochen, genauer darauf ein. Hier ist nur mal die Vollständige Prozedur:
procedure UpdateMovement;
const
RotXAxis : TVector3f = (1, 0, 0);
RotYAxis : TVector3f = (0, 1, 0);
RotZAxis : TVector3f = (0, 0, 1);
var
Direction : single;
LookVec : TVector4f;
begin
// Ist die Vorwärts-Taste gedrückt? Wenn ja, nach vorne gehen.
if Keys[VK_UP] then Direction := 1 else
// Ist die Rückwärtstaste gedrückt? Wenn ja, nach hinten gehen.
if Keys[VK_DOWN] then Direction := -1 else
// Wenn keine der beiden Tasten gedrückt wurde, kann die Prozedur
// verlassen werden, da dann keine Positions-Anpassung notwendig
// ist
Exit;
// Den Blickrichtungs-Vektor initialisieren. Hier soll nur nach vorne,
// also in die Y-Richtung geschaut werden.
LookVec[0] := 0;
LookVec[1] := 1;
LookVec[2] := 0;
// Den W-Wert auf 0 setzen. Wir benötigen ihn nicht.
LookVec[3] := 0;
// Den Look-Vektor zuerst um die Z-Achse...
RotateVector(LookVec, RotZAxis, -DegToRad(RotateZ));
// ...um die Y-Achse...
RotateVector(LookVec, RotYAxis, -DegToRad(RotateY));
// ... und um die X-Achse drehen.
RotateVector(LookVec, RotXAxis, -DegToRad(RotateX));
// Nun den gedrehten Vector zum Aktuellen Positions-Vektor
// hinzuzählen. Damit die Bewegung beachtet wird, das ganze
// um den Speed-Faktor 0.01 mal Direction multiplizieren.
PosVect[0] := PosVect[0] + (LookVec[0] * (Direction * 0.01));
PosVect[1] := PosVect[1] + (LookVec[1] * (Direction * 0.01));
PosVect[2] := PosVect[2] + (LookVec[2] * (Direction * 0.01));
end;
Eigentlich gar nicht viel, oder?!? Fangen wird am Anfang an. Wenn ich das Objekt in seiner Position verändern will (durch betätigen der Oben bzw. Unten Tasten), so muss ich zuerst einmal feststellen, in welche Richtung das Objekt verschoben werden soll:
// Ist die Vorwärts-Taste gedrückt? Wenn ja, nach vorne gehen.
if Keys[VK_UP] then Direction := 1 else
// Ist die Rückwärtstaste gedrückt? Wenn ja, nach hinten gehen.
if Keys[VK_DOWN] then Direction := -1 else
// Wenn keine der beiden Tasten gedrückt wurde, kann die Prozedur
// verlassen werden, da dann keine Positions-Anpassung notwendig
// ist
Exit;
Sollte keine der beiden Tasten betätigt worden sein, dann MUSS die Funktion verlassen werden, um keine falschen Rechnungen durchzuführen. Sonst kann es sein, dass sich das Objekt ohne eure Kontrolle dauernd verschiebt. Ok, wenn ich also nach oben gehen will, wird Direction auf 1 und anderen Falls auf -1 gesetzt. Ich Denke, der Grund dürfte Klar sein: 1 -> vorwärts und -1 -> Rückwärts. Das ganze basiert auf einfachste Mathematik ;o) (Ja, wirklich, man benötigt kein ABI, um 3D-Progger zu sein!!!)
Als nächstes wird mein Richtungs-Vektor initialisiert. Der 2 Eintrag (Y Achse) wird auf 1 gesetzt, da der Richtungs-Vektor in der Null-Stellung des Objektes parallel zur Y Achse steht. Der Grund: das Objekt "blickt" am Anfang oder nach einem Reset auf die Caption des Fensters.
// Den Blickrichtungs-Vektor initialisieren. Hier soll nur nach vorne,
// also in die Y-Richtung geschaut werden.
LookVec[0] := 0;
LookVec[1] := 1;
LookVec[2] := 0;
// Den W-Wert auf 0 setzen. Wir benötigen ihn nicht.
LookVec[3] := 0;
Lasst euch von der letzten Zeile nicht irritieren. Es gibt auch noch Vektoren welche einen W-Wert haben. Die RotateVector Funktion arbeitet mit einem solchen Vektor, da bei der Rotation ein Vektor mit einer Rotations-Matrix verrechnet wird, und diese eben ein 4x4 Feld hat. Aus diesem Grund wurde auch der TVector4f Typ verwendet. -> Ignoriert es einfach, der Wert wird sowieso nicht benötigt und sollte deswegen auf 0 stehen.
Nun wird der Vektor um die 3 Achsen gedreht. Da die RotateVector-Funktion einen "Standard-Vektor" (also mit X, Y und Z Wert) benötigt um zu wissen, um welche Achse gedreht werden soll, sind diese am Anfang der Prozedur im const-Bereich als Rot[Achse]Axis definiert. Das ist übrigens das gleiche wie bei glRotate, nur das dort die X, Y und Z Werte getrennt und nicht in einem Vektor zusammengefasst übergeben werden. Hier ist es übrigens auch sehr wichtig, die umgekehrte Reihenfolge zu verwenden. Also zuerst Drehung um die Z, dann um die Y und zum Schluss um die X Achse. Warum weis ich leider auch nicht. Der Winkel muss hier in einen RAD konvertiert werden, da die Funktion nicht mit GRAD angaben arbeitet. Außerdem muss der Winkel noch Invertiert, also mit einem - versehen werden, da sonst der Vektor in die entgegengesetzte Richtung zum Objekt gedreht wird. Ist nicht das was wir wollen. Warum genau, kann ich nicht so direkt erklären. Aber man muss auch nicht alles wissen ;o) Wenn es aber doch jemand weis warum, darf er mir das durchaus mitteilen. Ich lerne gerne dazu!
// Den Look-Vektor zuerst um die Z-Achse...
RotateVector(LookVec, RotZAxis, -DegToRad(RotateZ));
// ...um die Y-Achse...
RotateVector(LookVec, RotYAxis, -DegToRad(RotateY));
// ... und um die X-Achse drehen.
RotateVector(LookVec, RotXAxis, -DegToRad(RotateX));
Eigentlich gar nicht schwer, oder?!?
Ein kleiner Ausflug
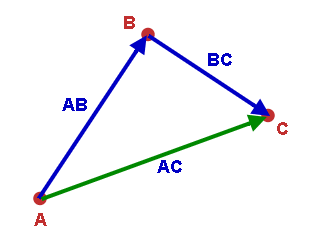
Ok, ganz ohne Mathematik geht es leider doch nicht. Jetzt haben wird den gedrehten Vektor und wissen, in welcher Richtung vorne liegt. Aber wie bekomme ich aus dieser Information meine neue Objekt-Position?!? Das Stichwort heißt: Vektor-Arithmetik. Keine Angst, ist nicht schlimm. Folgende "Skizze" soll helfen, sich das Ganze vorzustellen:
Wir haben einen Vektor, welcher von A nach B zeigt (ich nenne ich AB). Und wird haben einen, welcher von B nach C Zeigt (BC). Letzterer ist unser Richtungs-Vektor. Ok, so weit so gut, aber wir benötigen einen neuen Positions-Vektor : AC. Denn die neue Position ist C also muss ein Vektor von A (Ursprung) nach C (neue Position) zeigen. Den erhalten wir ganz einfach. Wirklich kein Problem. Einfachste Mathematik:
- AC = AB + BC
Boah ey... cool, oder? So einfach und schon haben wir die neue Position. DAS war Vektor-Arithmetik. Ein Kumpel sagte mal, das Matrizen und Vektoren Rechnung eigentlich wirklich nicht kompliziert ist. Und er hatte recht. +, - ,* und / ist doch wirklich kein Problem, oder?!?
Das neue Ziel
Ok, nun addieren wir einfach die beiden Vektoren miteinander. Der Richtungs-Vektor muss nur noch etwas "verlängert" werden. Denn bisher haben wir nur die Richtung. Das ganze mit einer Zahl (z.B. 5) multiplizieren, und wir haben unser Objekt 5 Schritte in Blickrichtung bewegt. Hä?!? Warum soll bitte Mathe für 3D-Progger schwer sein?!?
Ich habe das ganze hier so gelöst: Ich multipliziere den Vektor mit der Geschwindigkeit, mit welcher er sich bewegen soll. Erinnert ihr euch noch an Direction? Ja? Gut. Denn somit haben wir die Schritt-Weite. Entweder ein Schritt nach vorne, oder -1 Schritt nach vorne was einem Schritt nach hinten entspricht! Das ganze sieht dann so aus:
// Nun den gedrehten Vektor zum Aktuellen Positions-Vektor
// hinzuzählen. Damit die Bewegung beachtet wird, das ganze
// um den Speed-Faktor 0.01 mal Direction multiplizieren.
PosVect[0] := PosVect[0] + (LookVec[0] * (Direction * 0.01));
PosVect[1] := PosVect[1] + (LookVec[1] * (Direction * 0.01));
PosVect[2] := PosVect[2] + (LookVec[2] * (Direction * 0.01));
0.01 ist hier dann die Geschwindigkeit und kann nach Lust und Laune von Euch verändert werden.
Happy End?!?
Wie, DAS war alles? Ja. Es ist gar nicht so schwer wenn man weis, wie es geht. Und dank der Funktionen der Geometry.pas wird einem einiges abgenommen. Die Rotation eines Vektors selber ist eigentlich auch nicht sooo kompliziert, nur IMO etwas schwer zu erklären.
Und wie geht's jetzt weiter?
Das liegt an Euch. Wie gesagt: in unserem Beispiel bewegt sich das Objekt nicht ganz so, wie man es von einem Raumgleiter gewöhnt ist. Das Problem ist ganz einfach erklärt: Das Objekt dreht sich immer um das globale Koordinatensystem. Um also die richtige Drehung durch zu führen, muss ein lokales Koordinatensystem mitgeführt werden. Also 3 Vektoren anstelle von einem. Aber dafür gibt's später mal ein anderes Tutorial. Jetzt geht's erst mal in Urlaub ;o)
Außerdem ist hier überhaupt kein Wert auf Optimierung gelegt worden, sondern es ging nur um das Verständnis der Materie selber.
Viel Spaß beim Proggen und liefert DGL ne menge Feedback!!!
Euer
SchodMC
Anhang
Hier findet ihr den Sourcode zu diesem Tutorial: tut_objmov_src_api ![]()
|
|
||
Vorhergehendes Tutorial: Tutorial Nachsitzen |
Nächstes Tutorial: Tutorial Objekt immer um eigene Achse drehen |
|
|
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen. |
||