Werkzeugkiste
| |
Diese Werkzeugkiste enthält hilfreiche Funktionen für Kollisionsberechnungen. Sie stammt aus dem Tutorial Kollision2 kann aber überall wo nötig benutzt werden. |
Inhaltsverzeichnis
- 1 Die Werkzeugkiste
- 1.1 Bewegungsvektor und Strahl
- 1.2 Die Ebene
- 1.3 Das Skalarprodukt
- 1.4 Abstand eines Punktes von der Ebene
- 1.5 Schnittpunkt eines Strahls mit einer Ebene
- 1.6 Kugelposition bei Berührung mit der Ebene
- 1.7 Kollision einer Kugel mit einem Punkt (Polygonecke)
- 1.8 Schnittpunkt einer Kugel mit einer Linie (Polygonkante)
- 1.9 Der "Inside-Polygon-Test"
Die Werkzeugkiste
Die folgende Sammlung von Funktionen kann zur Berechnung von Kollisionen erforderlich oder nützlich sein. Nicht alle Funktionen werden in dem beschriebenen Algorithmus eingesetzt, es kann aber sein (eigentlich hoffe ich es), dass der eine oder andere von euch an dem Algorithmus herumbasteln oder sogar einen eigenen Ansatz verfolgen möchte.
In der Werkzeugkiste sind keine Funktionen enthalten, die Bestandteil jeder halbwegs vollständigen Funktionssammlung sind. Funktionen wie z.B. SubtractVectors oder DotProduct werden hier also nicht mehr aufgeführt. Eine Anmerkung möchte ich jedoch zu NormalizeVector machen. Ich verwende dazu eine Form, die den Skalierungsfaktor zurückliefert, während der Vektor über einen Zeiger bearbeitet wird. Beispiel:
TVector velocity;
TVector normal_velocity = velocity;
double speed = NormalizeVector (&normal_velocity);
normal_velocity = MatrixVectorProduct (mat, normal_velocity);
velocity = ScaleVector (speed, normal_velocity);
Bewegungsvektor und Strahl
Die Bewegung eines Objektes wird als Vektor dargestellt, sofern es sich um eine gleichförmige, gradlinige Bewegung handelt. Wenn wir - wie in diesem Tutorial - nur ein einzelnes bewegtes Objekt betrachten, können wir die Bewegung in solche gradlinigen Bewegungsschritte zerlegen. Wir brauchen aber eine Möglichkeit, jeden Punkt auf diesem Weg zu beschreiben, was zur Liniengleichung führt:
P = A + t * V
A ist der Punkt, der die Position des Objektes angibt. Zu diesem Punkt wird ein Vektor V addiert, der mit t beliebig skaliert werden kann. Damit kann jede Position in Richtung V erreicht werden. Die entscheidende Variable ist t, denn sie bestimmt, wie weit P von A entfernt ist. Gleichungen zur Berechnung von Intersektionen werden infolgedessen nach t aufgelöst.
Es gibt 2 Möglichkeiten:
- Der Vektor V ist der Bewegungsvektor und hat somit dieselbe Länge wie der Bewegungsschritt. In diesem Fall liegt t im Bereich [0, 1], sofern sich der Punkt P auf dem Wegabschnitt befindet. Werte > 1 zeigen an, dass der Punkt in diesem Schritt nicht erreichbar ist.
- Der Vektor V ist normalisiert und gibt nur die Richtung der Bewegung an. Nun liefert t die absolute Entfernung von A.
Den Bewegungsvektor können wir auch als Strahl auffassen, und wenn wir einen Punkt bewegen (das kann z.B. ein Punkt auf der Kugeloberfläche sein) können die Strahl-Intersektions-Funktionen zum Tragen kommen, wie sie beim Raytracing verwendet werden.
Die Ebene
Nun, es dürfte wohl klar sein, dass wir mit den drei Punkten eines Dreiecks gleichzeitig die Ebene, auf der das Dreieck liegt, eindeutig bestimmen. Wenn wir jedoch mit einer Ebene rechnen wollen, müssen wir zu anderen Definitionen greifen. So kann eine Ebene auch durch ihre Normale pNormal und einen Punkt pOrigin, der irgendwo auf der Ebene liegt, beschrieben werden. Die Normale lässt sich bequem mit dem Kreuzprodukt berechnen, und den Punkt haben wir bereits, indem wir einen beliebigen Punkt des Dreiecks nehmen.
TVector PlaneNormal (TVector a, TVector b, TVector c)
{
TVector res;
TVector ab = SubtractVectors (b,a);
TVector ac = SubtractVectors (c,a);
res = CrossProduct (ab, ac);
NormalizeVector (&res);
return res;
}
Eine andere Definition verwendet ebenfalls die Normale pNormal, anstatt des Punktes aber die Ebenenkonstante pConstant, die sich aus dem Skalarprodukt (pOrigin * pNormal) ergibt:
double PlaneConstant (TVector pOrigin, TVector pNormal)
{
return -(DotProduct (pNormal, pOrigin));
}
Jede Ebene hat eine eindeutig festgelegte Vorder- und Rückseite, unabhängig von der Position des bewegten Objektes. Entscheidend ist dabei die Reihenfolge, in der wir die Vertices des Polygons an OpenGL übergeben. Gehen wir entgegen dem Uhrzeigersinn vor, definieren wir die Vorderseite. Nun ja, und von hinten betrachtet, haben wir die entgegengesetzte Reihenfolge. Diese Unterscheidung ist z.B. wichtig, um die Rückseite von der Kollision auszuschließen. - Im übrigen macht auch OpenGL von der eindeutigen Unterscheidung Gebrauch, z.B. beim Backface-Culling. Neben der Vertex-Reihenfolge gibt es noch ein zweites Merkmal für Vorder- und Rückseite, nämlich die Normale. Wenn wir auf die Vorderseite schauen, zeigt die Normale grundsätzlich in unsere Richtung. Es kommt immer wieder mal vor, dass wir ein Test-Polygon in die Landschaft stellen. Wenn wir die Vertex-Reihenfolge beachten, ist es kein Problem, uns die passende Normale vorzustellen, so dass wir sie direkt angeben können, ohne das Kreuzprodukt zu bemühen.
Das Skalarprodukt
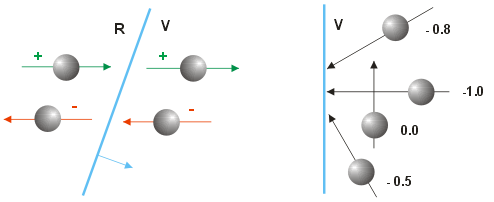
Wenn es um Kollisionsberechnungen geht, finden wir wohl kaum eine Funktion, in der keine Skalarprodukte vorkommen. Aber das meine ich hier nicht. Selbst in seiner nackten Form kann das Skalarprodukt aus der Normalen einer Ebene und dem Bewegungsvektor eine Menge über Kollisionen aussagen. Da haben wir zunächst das Vorzeichen. Ist das Produkt negativ, bewegt sich das Objekt auf die Vorderseite der Ebene zu, oder, wenn es sich auf der Rückseite befindet, von der Ebene weg. Und natürlich umgkehrt. Ist das Ergebnis 0, bewegt sich das Objekt parallel zur Ebene, und es kann z.B. keine Kollision an der Polygonfläche stattfinden.
Aber auch der Betrag sagt eine Menge aus. In diesem Fall muss der Bewegungsvektor normalisiert sein. Bei einem "Frontalzusammenstoß", also bei senkrechtem Aufprall ist das Ergebnis -1, und der Absolutbetrag nimmt ab, je flacher das Objekt mit der Ebene kollidiert - bis hin zum Grenzfall 0 (parallel zur Ebene). Zahlenmäßig ist das Ergebnis nichts anderes als der Cosinus des Winkels zwischen der Ebenen-Normalen und dem Bewegungsvektor.
Abstand eines Punktes von der Ebene
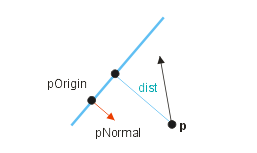
Es versteht sich, dass mit "Abstand" die kürzeste Entfernung zur Ebene gemeint ist. Wenn die Länge des Bewegungsvektors größer als dieser Abstand ist, kann beim besten Willen keine Kollision an der Ebene stattfinden. Zwar liefert das Ergebnis keinen Anhaltspunkt, wo das Objekt mit der Ebene kollidiert (die Richtung des Bewegungsvektors wird ja nicht berücksichtigt), aber für eine Vorsortierung kann die Rechnung ganz nützlich sein.
Das Ergebnis ist positiv, wenn sich der Punkt auf der Vorderseite der Ebene befindet, andernfalls negativ. Liegt der Punkt auf der Ebene, kommt natürlich 0 heraus.
Darüber hinaus erlaubt die Funktion, einen Punkt senkrecht auf die Ebene zu projizieren. Die Normale der Ebene wird mit dem berechneten, negativen Abstand skaliert und zur Position des Objektes addiert. Das Ergebnis ist der gewünschte Punkt auf der Ebene. Die Projektion kann u.a. zur Berechnung des Gleitpfades nach einer Kollision oder zur Zerlegung eines Bewegungsvektors in eine Gleitpfad- und eine Reibungskomponente benutzt werden.
double PlaneDistance (TVector pOrigin, TVector pNormal, TVector p)
{
// zunächst die Ebenen-Konstante
double d = -(DotProduct (pNormal, pOrigin));
return DotProduct (pNormal, p) + d;
}
Wenn die Ebenen-Konstante schon bekannt ist, vereinfacht sich die Funktion:
double PlaneDistanceT (TVector pNormal, double pConstant, TVector p)
{
return DotProduct (pNormal, p) + pConstant;
}
Projektion des Punktes auf die Ebene:
TVector ProjectPointToPlane (TVector pOrigin, TVector pNormal,
TVector p, TVector vel)
{
// vel muss normalisiert sein !
double d = -PlaneDistance (pOrigin, pNormal, p);
return (AddVectors (p, ScaleVector (d, vel));
}
Schnittpunkt eines Strahls mit einer Ebene
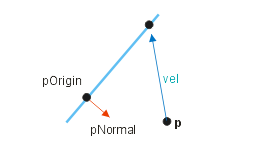
Die folgende Funktion dient dazu, die Entfernung eines Punktes zur Ebene zu ermitteln, und zwar in Bewegungsrichtung (nicht senkrecht wie bei der oben beschriebenen Funktion). Mit Hilfe dieser Entfernung können wir anschließend den Intersektionspunkt auf der Ebene berechnen. Den wiederum gebrauchen wir, um die Gleitebene zu bestimmen. Die Entfernung wird ferner benötigt, um bei mehreren möglichen Kollisionen die nächstliegende herauspicken zu können.
double PlaneIntersect (TVector pOrigin, TVector pNormal,
TVector p, TVector vel)
{
double d = -(DotProduct (pNormal, pOrigin));
double num = DotProduct (pNormal, p) + d;
double denom = DotProduct (pNormal, vel);
return -(num / denom);
}
Das Ergebnis ist der Faktor, mit dem der Bewegungsvektor vel zu multiplizieren ist. Der Vektor vel kann, muss aber nicht normalisiert sein (siehe oben). Der zweite Schritt besteht darin, den Intersektionspunkt zu berechnen, sofern es noch erforderlich sein sollte.
double dist =
PlaneIntersect (pOrigin, pNormal, p, vel);
TVector intersect_point =
AddVectors (p, ScaleVector (dist, vel));
Die beschriebene Strahl-Ebenen-Intersektion geht von einem bewegten Punkt aus. Wenn das kollidierende Objekt z.B. eine Kugel ist, muss der Punkt auf der Kugeloberfläche bekannt sein, der die Ebene im Kollisionsfall berührt.
Kugelposition bei Berührung mit der Ebene
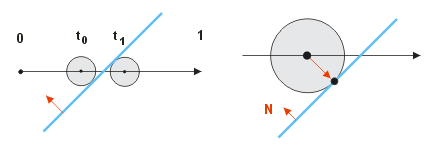
Mit der folgenden Funktion können wir ausrechnen, wie weit der Mittelpunkt (!) der Kugel bewegt werden muss, damit die Oberfläche der Kugel die Ebene berührt, entweder auf der Vorderseite oder auf der Rückseite. Das gilt auch für schrägen Aufprall.
double SpherePositionAtPlane (TVector pOrigin, TVector pNormal,
TVector p, TVector vel, double rad)
{
double dist = PlaneDistance (pOrigin, pNormal, p);
double denom = DotProduct (pNormal, vel);
return (rad - dist) / denom;
// alternativ für Rückseite der Ebene:
return (-rad - dist) / denom;
}
Kollision einer Kugel mit einem Punkt (Polygonecke)
Die folgende Funktion berechnet die absolute Entfernung einer bewegten Kugel bis zur Berührung mit einem feststehenden Punkt. Im Falle, dass keine Kollision stattfindet, wird -1 zurückgeliefert. Neben der Position pos, dem Bewegungsvektor vel und dem Radius rad der Kugel wird eine maximale Entfernung max angegeben. qlen ist nichts anderes als die im voraus berechnete quadratische Länge des Bewegungsvektors.
double VertexIntersect (TVector pos, TVector vel, double qlen,
TVector p, double rad, double max)
{
double b = 2.0 * (DotProduct (vel, SubtractVectors (pos, p)));
double c = SquareDistance (p, pos) - rad * rad;
double d = b * b - 4.0 * qlen * c;
if (d < 0.0) return -1;
double root = (-b - sqrt (d)) / 2 / qlen;
if (root > 0.0 && root < max) return root;
return -1;
}
Die folgende Funktion kann gut zur reversen Intersektion verwendet werden. Vom Punkt p aus wird ein Strahl in Richtung dir (normalisiert, umgekehrte Richtung wie Bewegung der Kugel) zur Kugel mit dem Mittelpunkt center und dem Radius rad geschickt. Die Funktion liefert die absolute Entfernung des nächsten Schnittpunktes zurück, im Negativfall -1.
double SphereIntersect (TVector center, double rad,
TVector p, TVector dir)
{
TVector q = SubtractVectors (center, p);
double c = VectorLength (q);
double v = DotProduct (q, dir);
double d = rad * rad - (c * c - v * v);
if (d < 0.0) return -1;
return v - sqrt(d);
}
Schnittpunkt einer Kugel mit einer Linie (Polygonkante)
Diese Funktion berechnet die absolute Entfernung einer bewegten Kugel bis zur Berührung mit einer Polygonkante. Die Parameter entsprechen weitgehend denen der vorherigen Funktion, nur dass diesmal natürlich 2 Punkte angegeben werden. In *cp wird außerdem der Intersektionspunkt zurückgegeben.
double EdgeIntersect (TVector pos, TVector vel, double qlen,
TVector p1, TVector p2, double rad, double max, TVector *cp)
{
TVector edge = SubtractVectors (p2, p1);
TVector btv = SubtractVectors (p1, pos);
double len = SquareLength (edge);
double dot1 = DotProduct (edge, vel);
double dot2 = DotProduct (edge, btv);
double dot3 = DotProduct (vel, btv);
double a = len * -qlen + dot1 * dot1;
double b = 2.0 * (len * dot3 - dot1 * dot2);
double c = len * (rad * rad - SquareLength (btv)) + dot2 * dot2;
double d = b * b - 4.0 * a * c;
if (d < 0.0) return -1;
double root = (-b + sqrt (d)) / 2 / a;
if (root > 0 && root < max) {
double f = (dot1 * root - dot2) / len;
if (f >= 0.0 && f <= 1.0) {
*cp = AddVectors (p1, ScaleVector (f, edge));
return root;
}
}
return -1;
}
Der "Inside-Polygon-Test"
Der Zweck dieses Tests ist offensichtlich: Wenn wir feststellen, dass ein Objekt mit der Polygonebene kollidiert, müssen wir anschließend untersuchen, ob das "Treffen" innerhalb des Polygons stattfindet. Dazu dient die folgende Funktion. Da die Anzahl der Vertices beliebig sein kann, wird ein Zeiger auf das Vertex-Array übergeben, während num die Anzahl der Ecken angibt.
Aufpassen: Die Ebenen-Konstante plane_const bezieht sich nicht auf die Polygonebene, sondern auf Hilfsebenen, die auf den Polygonseiten aufgespannt werden. Also nicht einfach eine evtl. schon bekannte Ebenen-Konstante übernehmen.
TBool InsidePolygon (TVector *v, double num, TVector pNormal, TVector p)
{
double plane_const;
TVector normal;
int i, ii;
TBool outside = False;
for (i=0; i<num; i++) {
if (i == num-1) ii = 0; else ii = i + 1;
if (!outside) {
normal = CrossProduct (SubtractVectors (v[i], v[ii]), pNormal);
plane_const = PlaneConstant (v[i], normal);
if (DotProduct (p, normal) + plane_const < 0.0) outside = True;
}
}
return (!outside);
}
Die Funktion arbeitet nach dem Prinzip der "Rechts-links-Orientierung". Damit ist folgendes gemeint: Wenn wir entgegen dem Uhrzeigersinn über die Polygonseiten wandern, liegt der Punkt immer auf der linken Seite, sofern er sich innerhalb des Polygons befindet. Müssen wir einmal den Kopf nach rechts drehen, liegt der Punkt außerhalb.