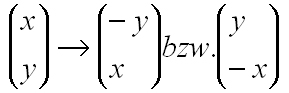Tutorial Separating Axis Theorem: Unterschied zwischen den Versionen
I0n0s (Diskussion | Beiträge) |
Seth (Diskussion | Beiträge) (Viel Code entfernt (liegt den Beispielen bei), kleine Fehler entfernt, Gerade wird nun stehts mit Achse betitelt) |
||
| Zeile 12: | Zeile 12: | ||
[[Bild:SAT_Normale.jpg|thumb|right]] | [[Bild:SAT_Normale.jpg|thumb|right]] | ||
| − | Das Separating Axis Theorem (kurz: SAT) besagt, dass zwei Polygone sich nicht schneiden, wenn es möglich ist, eine Gerade zu finden, die zwischen den beiden liegt. | + | Das Separating Axis Theorem (''kurz: SAT'') besagt, dass zwei Polygone sich nicht schneiden, wenn es möglich ist, eine Gerade zu finden, die zwischen den beiden liegt, bzw. die beiden trennt. |
| + | Daher auch der Name ''Separating Axis''. | ||
Nun gibt es unendlich viele Geraden die man testen könnte... | Nun gibt es unendlich viele Geraden die man testen könnte... | ||
Glücklicherweise kann man sich hier auf eine überschaubare Zahl beschränken, denn man braucht nur die Anzahl der Seiten beider Polygone. Bei einem Viereck wären das vier, bei einem Dreieck drei, etc. | Glücklicherweise kann man sich hier auf eine überschaubare Zahl beschränken, denn man braucht nur die Anzahl der Seiten beider Polygone. Bei einem Viereck wären das vier, bei einem Dreieck drei, etc. | ||
| Zeile 22: | Zeile 23: | ||
[[Bild:SAT_Normale_Formel.jpg]] | [[Bild:SAT_Normale_Formel.jpg]] | ||
| − | die Koordinaten werden vertauscht und eine von beiden wird negiert. | + | die Koordinaten werden vertauscht und eine von beiden wird negiert, so erhält man einen Vektor der senkrecht zu dem original Vektor ist. Da es zwei Möglichkeiten gibt, spricht man von der linken oder rechten Normale (aus der Sicht des Vektors). |
| − | Der Vektor muss dann noch normalisiert werden, sodass er die Länge 1 erhält. | + | Der Vektor muss dann noch normalisiert werden, sodass er die Länge 1 erhält,. |
| − | Jetzt müssen beide Polygone auf diesen Vektor | + | Jetzt müssen beide Polygone auf diesen Vektor projeziert werden, denn dadurch erhalten wir ein eindimensionales Abbild unserer Polygone und können mittels eines einfachen Vergleichs überprüfen, ob sich die beiden eindimensionalen Strecken schneiden. |
| + | Sollte ein Fall eintreffen bei dem kein Schnitt stattfindet, dann kollidieren die beiden Polygone nicht und die Prozedur kann abgebrochen werden. Dies ist auch der Grund, warum dieses Verfahren recht schnell ist, da im besten Fall schon im ersten | ||
| + | Durchlauf abgebrochen werden kann. | ||
| + | |||
Nun zur Projektion: | Nun zur Projektion: | ||
| Zeile 30: | Zeile 34: | ||
Auf dem linken Bild sieht man, wie beide Polygone auf die Gerade projiziert werden, der pinke Bereich zeigt die Schnittmenge an. In diesem Fall ist die Gerade die Normale der linken oder rechten Seite des Quadrats. | Auf dem linken Bild sieht man, wie beide Polygone auf die Gerade projiziert werden, der pinke Bereich zeigt die Schnittmenge an. In diesem Fall ist die Gerade die Normale der linken oder rechten Seite des Quadrats. | ||
| − | Auf dem Bild rechts ist der Fall dargestellt, dass keine Kollision stattfindet, demzufolge gibt es auch keine Schnittmenge auf der | + | Der Begriff "Gerade" ist hier allerdings nicht ganz korrekt. Eine Gerade hat eine räumliche Lage, diese ist für unser Vorhaben jedoch nicht von belangen, deshalb werde ich im Folgenden das Wort ''Achse'' benutzen, denn |
| − | + | wie der Name schon sagt, werden diese "Geraden" gemeinhin mit Trennungsachsen betitelt. | |
| + | Auf dem Bild rechts ist der Fall dargestellt, dass keine Kollision stattfindet, demzufolge gibt es auch keine Schnittmenge auf der Achse. | ||
| − | Für die Projektion eines Vektors auf einen anderen verwenden wir das [[Standard_Skalarprodukt|Skalarprodukt]], bei diesem kommt ein Zahlenwert heraus, der die Position des Eckpunktes auf unserer | + | Für die Projektion eines Vektors auf einen anderen verwenden wir das [[Standard_Skalarprodukt|Skalarprodukt]], bei diesem kommt ein Zahlenwert heraus, der die Position des Eckpunktes auf unserer eindimensionalen Achse darstellt. |
Haben wir sämtliche Punkte projiziert, so müssen wir für die jeweiligen Polygone noch jeweils den kleinsten und größten Wert heraussuchen, damit wir zwei Strecken erhalten. | Haben wir sämtliche Punkte projiziert, so müssen wir für die jeweiligen Polygone noch jeweils den kleinsten und größten Wert heraussuchen, damit wir zwei Strecken erhalten. | ||
| − | Diese werden dann auf Schnitt geprüft und das wars. | + | Diese werden dann mit einer einfachen Abfrage auf Schnitt geprüft und das wars. |
=== Zusammenfassung === | === Zusammenfassung === | ||
| − | *Jedes der beiden Polygone durchgehen und alle nötigen | + | *Jedes der beiden Polygone durchgehen und alle nötigen Achsen aus den Normalen der Seitenflächen bestimmen |
| − | **Jeden Eckpunkt jedes Polygons auf diese | + | **Jeden Eckpunkt jedes Polygons auf diese Achsen projizieren |
**Die kleinsten und größten Werte ermitteln und auf Schnitt prüfen | **Die kleinsten und größten Werte ermitteln und auf Schnitt prüfen | ||
*Tritt der Fall auf, dass kein Schnitt statt findet, so kann sofort abgebrochen werden, es findet keine Kollision statt. | *Tritt der Fall auf, dass kein Schnitt statt findet, so kann sofort abgebrochen werden, es findet keine Kollision statt. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Kollision eines Kreises und eines Polygons == | == Kollision eines Kreises und eines Polygons == | ||
| Zeile 358: | Zeile 55: | ||
Das Prinzip für die Kollision zweier Polygone ist denke ich jetzt klar geworden, doch was ist, wenn wir einen Kreis haben, der mit einem Polygon kollidiert? | Das Prinzip für die Kollision zweier Polygone ist denke ich jetzt klar geworden, doch was ist, wenn wir einen Kreis haben, der mit einem Polygon kollidiert? | ||
Dieser Fall ist leicht abzuhandeln, ein Kreis hat unendlich viele Normalen, die man testen könnte, | Dieser Fall ist leicht abzuhandeln, ein Kreis hat unendlich viele Normalen, die man testen könnte, | ||
| − | uns reichen aber die, die die Vertices des Polygons schneiden würden, sprich: die | + | uns reichen aber die, die die Vertices des Polygons schneiden würden, sprich: die Achsen, die den Kreismittelpunkt und die Ecken unseres Polygons verbinden würden. |
[[Bild:SAT_Kreis_Quadrat.jpg|thumb|right]] | [[Bild:SAT_Kreis_Quadrat.jpg|thumb|right]] | ||
| − | Die blauen Linien auf dem Bild sind wieder einmal | + | Die blauen Linien auf dem Bild sind wieder einmal die Achsen auf die wir projizieren, diese kommen zu den, die wir aus dem Polygon berechnen hinzu. |
=== Zusammenfassung === | === Zusammenfassung === | ||
| Zeile 370: | Zeile 67: | ||
*Der Kreis wird projiziert, indem der Vektor, auf den wir multiplizieren, mit dem Radius des Kreises skaliert (also skalar multipliziert) wird. Mit diesem wird dann genauso weiter verfahren. Dies ist dann der Max-Wert für unseren Kreis, der Min-Wert ist einfach der Max-Wert * -1, also -max. | *Der Kreis wird projiziert, indem der Vektor, auf den wir multiplizieren, mit dem Radius des Kreises skaliert (also skalar multipliziert) wird. Mit diesem wird dann genauso weiter verfahren. Dies ist dann der Max-Wert für unseren Kreis, der Min-Wert ist einfach der Max-Wert * -1, also -max. | ||
| − | + | Hierzu ist zu sagen, dass dies noch dahingehend optimieren kann, dass man feststellt, in welcher Voronoi-Region des Polygons sich der Kreis befindet. Wenn man diese Region hat, reicht es eine Achse zu prüfen. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Kollision eines Punktes und eines Polygons == | == Kollision eines Punktes und eines Polygons == | ||
| Zeile 473: | Zeile 73: | ||
Ganz am Rande möchte ich noch erwähnen, dass es ebenso möglich ist, zu prüfen, ob sich ein Punkt in einem Polygon befindet. Hierzu wird einfach der Punkt auf die Achsen projiziert und geprüft ob er größer als das Minimum und kleiner als das Maximum des Polygons auf dieser Achse ist. | Ganz am Rande möchte ich noch erwähnen, dass es ebenso möglich ist, zu prüfen, ob sich ein Punkt in einem Polygon befindet. Hierzu wird einfach der Punkt auf die Achsen projiziert und geprüft ob er größer als das Minimum und kleiner als das Maximum des Polygons auf dieser Achse ist. | ||
| − | |||
| − | |||
| − | |||
== Polygone trennen == | == Polygone trennen == | ||
| − | + | Damit unsere Kollisionserkennung praxistauglich wird, müssen die Polygone, wenn sie kollidieren auch wieder getrennt werden können. Hierzu benötigen wir einen Vektor, der unsere beiden Polygone wieder auseinander "schiebt". Selbstverständlich könnte man einen beliebigen Vektor nehmen, aber das Ergebnis wäre eher realtitätsfern, deshalb brauchen wir den Vektor, der den kürzesten Weg beschreibt, um die beiden Polygone zu trennen. Dieser Vektor wird auch '''MTD'''-Vektor genannt (für '''M'''inimum '''T'''ranslation '''D'''istance). Hier kommt ein weiterer Vorteil des Separating Axis Theorems zum tragen, denn den Vektor den wir suchen, haben wir schon so gut wie berechnet. | |
| − | + | Wir multiplizieren alle unsere Projektionsachsen mit den Differenzen, die wir bei den eindimensionalen Kollisionen herausbekommen haben, somit erhalten wir Vektoren, die für das Außeinander-Schieben unserer Polygonein in Frage kommen. Nun müssen wir nur noch den kürzesten davon finden, dies ist unser MTD. | |
| − | Damit unsere Kollisionserkennung praxistauglich wird, müssen die Polygone, wenn sie kollidieren auch wieder getrennt werden können. Hierzu benötigen wir einen Vektor, der unsere beiden Polygone wieder auseinander "schiebt". Selbstverständlich könnte man einen beliebigen Vektor nehmen, aber das Ergebnis wäre eher realtitätsfern, deshalb brauchen wir den Vektor, der den kürzesten Weg beschreibt, um die beiden Polygone zu trennen. Dieser Vektor wird auch '''MTD'''-Vektor genannt ('''M'''inimum '''T'''ranslation '''D'''istance). Hier kommt ein weiterer Vorteil des Separating Axis Theorems zum tragen, denn den Vektor den wir suchen, haben wir schon so gut wie berechnet. | ||
| − | Wir multiplizieren alle unsere Projektionsachsen mit den Differenzen, die wir bei den eindimensionalen Kollisionen herausbekommen haben, somit erhalten wir Vektoren, die für das Außeinander-Schieben unserer | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Das Beispielprojekt == | == Das Beispielprojekt == | ||
Version vom 19. September 2007, 20:44 Uhr
Inhaltsverzeichnis
Kollisionserkennung
von Polygonen mit dem Separating Axis Theorem
Vorwort
In diesem Tutorial möchte ich eine schnelle Variante zur Kollision zweier konvexer Polygone erläutern. Diese kann nachträglich für konkave Polygone und andere Objekte wie Kreise und abgerundete Objekte verwendet werden. Um den mathematischen Hintergrund zu verstehen, ist es sinnvoll ein wenig Kenntnis in Vektorrechnung zu haben.
Kollision zweier Polygone
Die Theorie
Das Separating Axis Theorem (kurz: SAT) besagt, dass zwei Polygone sich nicht schneiden, wenn es möglich ist, eine Gerade zu finden, die zwischen den beiden liegt, bzw. die beiden trennt. Daher auch der Name Separating Axis. Nun gibt es unendlich viele Geraden die man testen könnte... Glücklicherweise kann man sich hier auf eine überschaubare Zahl beschränken, denn man braucht nur die Anzahl der Seiten beider Polygone. Bei einem Viereck wären das vier, bei einem Dreieck drei, etc. Hat man die Eckpunkte des Polygons als Vektoren (Ortsvektoren) gegeben, kann man durch Subtraktion zweier Ortsvektoren den Vektor bestimmen der zu der Seite gehört, die von den beiden Vektoren aufgespannt wird.
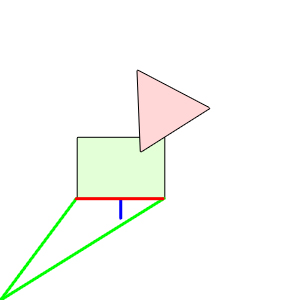
Auf dem Bild rechts ist ein Beispiel zu sehen. Dort ist ein Quadrat, die grünen Striche bezeichnen die Ortsvektoren der Eckpunkte, der rote Strich ist die berechnete Seite. Was wir aber brauchen ist der blaue Strich, das ist die Normale der Seite. Die Normale berechnet sich folgendermaßen:
die Koordinaten werden vertauscht und eine von beiden wird negiert, so erhält man einen Vektor der senkrecht zu dem original Vektor ist. Da es zwei Möglichkeiten gibt, spricht man von der linken oder rechten Normale (aus der Sicht des Vektors). Der Vektor muss dann noch normalisiert werden, sodass er die Länge 1 erhält,. Jetzt müssen beide Polygone auf diesen Vektor projeziert werden, denn dadurch erhalten wir ein eindimensionales Abbild unserer Polygone und können mittels eines einfachen Vergleichs überprüfen, ob sich die beiden eindimensionalen Strecken schneiden. Sollte ein Fall eintreffen bei dem kein Schnitt stattfindet, dann kollidieren die beiden Polygone nicht und die Prozedur kann abgebrochen werden. Dies ist auch der Grund, warum dieses Verfahren recht schnell ist, da im besten Fall schon im ersten Durchlauf abgebrochen werden kann.
Nun zur Projektion:
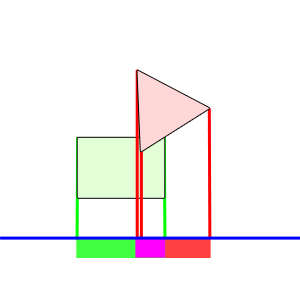
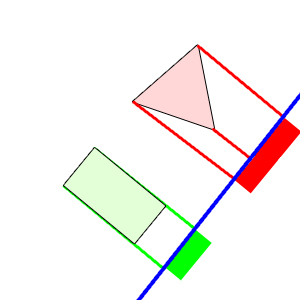
Auf dem linken Bild sieht man, wie beide Polygone auf die Gerade projiziert werden, der pinke Bereich zeigt die Schnittmenge an. In diesem Fall ist die Gerade die Normale der linken oder rechten Seite des Quadrats. Der Begriff "Gerade" ist hier allerdings nicht ganz korrekt. Eine Gerade hat eine räumliche Lage, diese ist für unser Vorhaben jedoch nicht von belangen, deshalb werde ich im Folgenden das Wort Achse benutzen, denn wie der Name schon sagt, werden diese "Geraden" gemeinhin mit Trennungsachsen betitelt. Auf dem Bild rechts ist der Fall dargestellt, dass keine Kollision stattfindet, demzufolge gibt es auch keine Schnittmenge auf der Achse.
Für die Projektion eines Vektors auf einen anderen verwenden wir das Skalarprodukt, bei diesem kommt ein Zahlenwert heraus, der die Position des Eckpunktes auf unserer eindimensionalen Achse darstellt. Haben wir sämtliche Punkte projiziert, so müssen wir für die jeweiligen Polygone noch jeweils den kleinsten und größten Wert heraussuchen, damit wir zwei Strecken erhalten. Diese werden dann mit einer einfachen Abfrage auf Schnitt geprüft und das wars.
Zusammenfassung
- Jedes der beiden Polygone durchgehen und alle nötigen Achsen aus den Normalen der Seitenflächen bestimmen
- Jeden Eckpunkt jedes Polygons auf diese Achsen projizieren
- Die kleinsten und größten Werte ermitteln und auf Schnitt prüfen
- Tritt der Fall auf, dass kein Schnitt statt findet, so kann sofort abgebrochen werden, es findet keine Kollision statt.
Kollision eines Kreises und eines Polygons
Theorie
Das Prinzip für die Kollision zweier Polygone ist denke ich jetzt klar geworden, doch was ist, wenn wir einen Kreis haben, der mit einem Polygon kollidiert? Dieser Fall ist leicht abzuhandeln, ein Kreis hat unendlich viele Normalen, die man testen könnte, uns reichen aber die, die die Vertices des Polygons schneiden würden, sprich: die Achsen, die den Kreismittelpunkt und die Ecken unseres Polygons verbinden würden.
Die blauen Linien auf dem Bild sind wieder einmal die Achsen auf die wir projizieren, diese kommen zu den, die wir aus dem Polygon berechnen hinzu.
Zusammenfassung
- Wir berechnen also den Vektor vom Kreis-Mittelpunkt zum Vertex, dieser wird normalisiert.
- Dann projizieren wir das Polygon wie gehabt
- Der Kreis wird projiziert, indem der Vektor, auf den wir multiplizieren, mit dem Radius des Kreises skaliert (also skalar multipliziert) wird. Mit diesem wird dann genauso weiter verfahren. Dies ist dann der Max-Wert für unseren Kreis, der Min-Wert ist einfach der Max-Wert * -1, also -max.
Hierzu ist zu sagen, dass dies noch dahingehend optimieren kann, dass man feststellt, in welcher Voronoi-Region des Polygons sich der Kreis befindet. Wenn man diese Region hat, reicht es eine Achse zu prüfen.
Kollision eines Punktes und eines Polygons
Ganz am Rande möchte ich noch erwähnen, dass es ebenso möglich ist, zu prüfen, ob sich ein Punkt in einem Polygon befindet. Hierzu wird einfach der Punkt auf die Achsen projiziert und geprüft ob er größer als das Minimum und kleiner als das Maximum des Polygons auf dieser Achse ist.
Polygone trennen
Damit unsere Kollisionserkennung praxistauglich wird, müssen die Polygone, wenn sie kollidieren auch wieder getrennt werden können. Hierzu benötigen wir einen Vektor, der unsere beiden Polygone wieder auseinander "schiebt". Selbstverständlich könnte man einen beliebigen Vektor nehmen, aber das Ergebnis wäre eher realtitätsfern, deshalb brauchen wir den Vektor, der den kürzesten Weg beschreibt, um die beiden Polygone zu trennen. Dieser Vektor wird auch MTD-Vektor genannt (für Minimum Translation Distance). Hier kommt ein weiterer Vorteil des Separating Axis Theorems zum tragen, denn den Vektor den wir suchen, haben wir schon so gut wie berechnet. Wir multiplizieren alle unsere Projektionsachsen mit den Differenzen, die wir bei den eindimensionalen Kollisionen herausbekommen haben, somit erhalten wir Vektoren, die für das Außeinander-Schieben unserer Polygonein in Frage kommen. Nun müssen wir nur noch den kürzesten davon finden, dies ist unser MTD.
Das Beispielprojekt
Beispiel 1 - Polygon <> Polygon
Was wäre ein Tutorial doch ohne Beispiel ;) Ich werde hier nur kurz die Verwendung des Codes erläutern und ein kleines Beispielprogramm anhängen. Ein Polygon muss natürlich erst einmal erzeugt werden:
A := TPolygon.Create;
Die einfachste Möglichkeit es zu gestalten funktioniert so:
with A do
begin
position := to_v2f(200, 200);
AddVertex(to_v2f(50, -50));
AddVertex(to_v2f(50, 50));
AddVertex(to_v2f(-50, 50));
AddVertex(to_v2f(-50, -50));
end;
Dies liefert ein Quadrat mit den Maßen 100*100 an der Position (200|200). Die Koordinaten der Vertices werden absolut zur Position und entgegen des Uhrzeigersinns angegeben.
Zeichnen kann man das Polygon dann ganz einfach so:
procedure TMainForm.DrawPolygon(A: TPolygon);
var
i, l: integer;
begin
for i := 0 to A.Count - 1 do
begin
l := i + 1;
if l > (A.Count - 1) then
l := 0;
Image1.Canvas.MoveTo(round(A.vertices_abs[l].x), round(A.vertices_abs[l].y));
Image1.Canvas.LineTo(round(A.vertices_abs[i].x), round(A.vertices_abs[i].y));
end;
end;
Und hier das Beispielprojekt:
Exe: http://www.exec-dev.de/SAT_Tutorial/SAT_exe.zip
Source: http://www.exec-dev.de/SAT_Tutorial/SAT_src.zip
Beispiel 2 - Kreis <> Polygon
Für den Kreis ist die Verwendung im Prinzip die selbe, mit:
C := TCircle.Create;
wird zunächst ein Kreis erzeugt und mit Position und Padius bekommt er seine Werte zugewiesen. Gezeichnet wird er mittels:
procedure TMainForm.DrawCircle(C: TCircle; aColor: TColor);
begin
with Image1.Canvas do
begin
Pen.Color := aColor;
Ellipse(round(C.position.x - C.radius), round(C.position.y - C.radius),
round(C.position.x + C.radius), round(C.position.y + C.radius));
end;
end;
Und hier das Beispielprojekt für die Kollision Kreis <> Polygon:
Exe: http://www.exec-dev.de/SAT_Tutorial/SAT_Kreis_exe.zip
Source: http://www.exec-dev.de/SAT_Tutorial/SAT_Kreis_src.zip
Beispiel 3 - Trennung von Polygonen
In diesem Beispiel wird ein Polygon mittels:
B.position := v2f_sub(B.position, MTD);
verschoben, sodass die beiden Polygone sich nicht schneiden. Es ließen sich auch beide um die Hälfte des Vektors verschieben, dies hängt von der Anwendung ab.
Hier gibt es die Exe und den Code für die Trennung von Polygonen:
Exe: http://www.exec-dev.de/SAT_Tutorial/SAT_Trennung_exe.zip
Source: http://www.exec-dev.de/SAT_Tutorial/SAT_Trennung_src.zip
Quellen
SAT-Tutorial(Eng) [1]
SAT-Tutorial(Eng / VB) [2]
Nachwort
Ich hoffe das Tutorial war nicht zu trocken und hat vielleicht auch ein wenig Spass gemacht und weitergeholfen. Für Fragen, Vorschläge, Ergänzungen, etc. bin ich selbstverständlich offen.
mfg