Reflexion: Unterschied zwischen den Versionen
(→Reflexion: Reflexionen in Ray-Tracern beschrieben) |
K (→Reflexionen in Ray-Tracern) |
||
| Zeile 15: | Zeile 15: | ||
Weil man es mit dem Einheitskreis zu tun hat, kann den Hilfsvektor p unterhalb von n durch cos(γ)*n bestimmen und weil cos(γ) gerade das Skalarprodukt zwischen n und v ist, gilt: | Weil man es mit dem Einheitskreis zu tun hat, kann den Hilfsvektor p unterhalb von n durch cos(γ)*n bestimmen und weil cos(γ) gerade das Skalarprodukt zwischen n und v ist, gilt: | ||
[[Bild:Reflexion_Hilfsvektor.png|center]] | [[Bild:Reflexion_Hilfsvektor.png|center]] | ||
| − | Bei genauer Betrachtung stellt man fest, daß dieser Vektor p auch am rechten Rand auftaucht | + | Bei genauer Betrachtung stellt man fest, daß dieser Vektor p auch am rechten Rand auftaucht. Bilded man dann eine geschlossene Vektorkette, so ergibt sich: |
[[Bild:Reflexion_Formelrechnung.png|center]] | [[Bild:Reflexion_Formelrechnung.png|center]] | ||
Version vom 24. Dezember 2006, 15:07 Uhr
(Mehr Informationen/weitere Artikel) {{{1}}} |
Inhaltsverzeichnis
Reflexion
Überischt
Reflexionen treten in unserer Umgebung häufig auf. Der Spiegel an der Wand, das eigene verzerrte Abbild im Löffel oder deutlich subtiler auf eigentlich matten Gegenständen, auf denen man sich mit etwas mühe recht unscharf erkennen kann. Sie treten so häufig auf, daß der Versuch virtuelle Umgebungen photorealistisch anzuzeigen, ohne Reflexionen darzustellen, scheitern muss. Tatsächlich zähle ich auf meinem halbwegs aufgeräumten Schreibtisch 13 Gegenstände, in denen man sich deutlich spiegeln kann.
Reflexionen in OpenGl
ich möchte erstellt werden
Reflexionen in Ray-Tracern
Angenommen sei ein Strahl, der aus der Richtung v (normiert) auf eine Oberfläche mit Normale r (auch normiert) trifft. Dann bestimmt sich die Reflexions-Richtung durch die Formel:
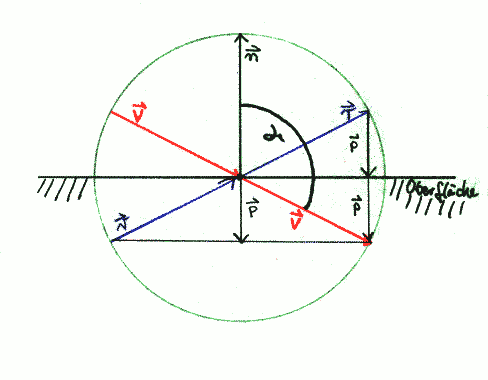
Wie entsteht diese Formel: Man zeiche die gegebene Situation auf. Der Kreis beschreibe den Einheitskreis ( wir haben es ja mit normierten Vektoren zu tun ). Der Normalenvektor und die Oberfläche werden ohne weiteres eingezeichnet. Die eintreffende Richtung v und die Refexionsrichtung werden einmal ankommend und einmal abgehend am Schnittpunkt eingezeichnet. Dann kann man den spitzeren Winkel γ leicht einmalen, der zwischen n und v ist:
Weil man es mit dem Einheitskreis zu tun hat, kann den Hilfsvektor p unterhalb von n durch cos(γ)*n bestimmen und weil cos(γ) gerade das Skalarprodukt zwischen n und v ist, gilt:
Bei genauer Betrachtung stellt man fest, daß dieser Vektor p auch am rechten Rand auftaucht. Bilded man dann eine geschlossene Vektorkette, so ergibt sich:
Siehe auch
Environment_Mapping, Cube Mapping, Sphere Mapping (am Ende), Stencilpuffer