Interpolation

Bei Interpolationsverfahren geht es darum, aus wenigen Werten beliebig viele Werte zu generieren. Da die gegebenen Werte - wo Interpolation nötig ist - meistens als Stichproben gesehen werden können, werden verschiedenste Verfahren benötigt um auch die nicht gegebenen Werte den Ansprüchen entsprechend zu berechnen. Die Ansprüche variieren hierbei etwas anhand der Geschwindigkeitsanforderungen, des Zahlenraumes und nicht zuletzt anhand der Art und Weise wie man interpolieren möchte.

Polynom Interpolationen

Wenn man N gegebene Werte hat, so kann man diese mit einem Polynom (N-1)ten Grades interpolieren. Eine Polynom Interpolationen besitzen die allgemeine Form:

I = (t^n)*Fn + (t^(n-1))*F(n-1) + ... + t*F1 + F0

Wobei:

t ... die Interpolationsposition im Wertebereich [0|1]
Fx ... ein konstanter Wert oder Faktor (oder allgemein ein m-Dimensionaler Vektor)
I ... das interpolierte Ergebnis, was ebenfalls ein einzelner Wert oder ein Vektor sein kann.

Durch die Vektor-Schreibweise sollte bereits klar sein, dass Polynom-Interpolationen für jede Dimension extrig berechnet werden, und somit auf beliebig viele Dimensionen erweiterbar sind.

Lineare Interpolation

Allgemein

Die einfachste Form einer Polynom-Interpolation ist die lineare Interpolation. Hierbei sind nur 2 Werte gegeben, somit kann man diese Werte mit einem Polynom ersten Grades interpolieren. Dieses ist (wie unschwer zu erraten) eine Gerade der Form:

I = t*F1 + F0

Diese (eher ungewöhnliche) Form der Geradengleichung entspricht der oben angegebenen Polynom-Interpolation in beliebiger Dimension. Die Berechnung der Faktoren Px erfolgt hier für jede Dimension getrennt. Gegeben seien 2 m dimensionale Punkte (A1, A2, ..., A(m-1), Am) und (B1, B2, ..., B(m-1), Bm). Nun lässt sich für jede Dimension d ein einfaches Gleichungssystem aufstellen:

Ad = 0*F1d + F0d
Bd = 1*F1d + F0d

da wir mit einem Interpolationswert von 0 den ersten Punkt (A) erhalten wollen und einem Interpolationswert von 1 den zweiten Punkt (B) möchten. Dies umgeformt auf P1d und P0d ergibt:

F0d = Ad
F1d = Bd - Ad

Diesen Rechenschritt wiederholen wir für jede Dimension.

Rechenbeispiel

Wir wollen 2 Punkte im 3 dimensionalen Raum interpolieren:

A: (2|5|0)
B: (4|1|8)

Wir berechnen uns die Vektoren P1 und P0 wie oben angegeben, wobei x die erste und z die dritte Dimension dar stellen soll:

F0x = Ax = 2
F1x = Bx - Ax = 2
F0y = Ay = 5
F1y = By - Ay = -4
F0z = Az = 0
F1z = Bz - Az = 8

Somit erhalten wir die unsere Interpolationsgleichung:

I(x|y|z) = t * (2|-4|8) + (2|5|0)

Das Ergebnis sieht nun folgendermaßen aus:

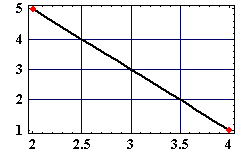
2 dimensionale Version des obigen Beispieles. Die gegebenen Punkte sind somit A(2|5) und B(4|1). Diese Punkte sind in rot dargestellt. Die Gerade beinhaltet alle Punkte für die gegebene Formel mit t im Wertebereich [0|1]

Polynome höheren Grades

Allgemein

Wie euch vielleicht schon bei der linearen Interpolation aufgefallen ist, ist eine Reihung der Punkte (vorher nur 2) erforderlich. Welcher PUnkt soll das Ergebnis mit t = 0 sein? Und welcher mit t=1? Wenn man mehr als 2 Punkte gegeben hat, so benötigt man zusätzlich noch die Informationen für welches t die beiden neuen Punkte gelten sollen. Meistens interpoliert man hier die Werte für t linear. Das heißt bei N gegebenen Punkten, soll der x-te Punkt für den t-Wert

t(Px) = x / (N-1) + 0

gegeben werden. Wobei:

t(Px) ... der t-Wert für den x-ten Punkt

Das (N-1) der Gleichung wird uns noch länger verfolgen, deshalb werden wir im weiteren Verlauf N-1 als n bezeichnen. Hier noch kurz die Anmerkung, dass man bei einem gegebenen Punkt natürlich keine Parameter benötigt sondern der Punkt immer gleich ist. Man kann sich dies (und alles darauffolgende) auch so vorstellen, dass wir den ersten gegebenen Punkt F0 als 0-Punkt annehmen und erst am "Ende" F0 addieren. Aus dieser Sichtweise heraus bekommen wir unser n = N-1.

Nun lässt sich wiederum das allgemeine (lineare) Gleichungssystem auffstellen:

P0 = t(P0)^n * Fn + t(P0)^(n-1) * F(n-1) + ... + t(P0) * F1 + F0
P1 = t(P1)^n * Fn + t(P1)^(n-1) * F(n-1) + ... + t(P1) * F1 + F0
...
Pn = t(Pn)^n * Fn + t(Pn)^(n-1) * F(n-1) + ... + t(Pn) * F1 + F0

Wobei:

Px ... der x-te Punkt
t(Px) ... der t-Wert für den x-ten Punkt
Fy ... der zu berechnende Faktor

Also ein Gleichungssystem mit n unbekannten und n (linear unabhängigen) Gleichungen, welches sich demnach eindeutig lösen lässt. Wobei dieses Gleichungssystem wiederum für jede Dimension extrig aufgestellt und berechnet werden muss! Da man (eindeutig lösbare) Gleichungssystem recht angenehm durch Matrizen-Mathematik lösen kann, empfiehlt sich auch folgende Schreibweise:

P = M * F

Wobei:

P ... ein N dimensionaler Vektor der die gegebenen Werte für den jeweiligen Punkt beinhaltet
M ... eine NxN Matrix welche die t(Px)^y beinhaltet
F ... ein N dimensionaler Vektor der die zu berechnenden Faktoren erhält
und N ... wie gehabt die Anzahl der gegebenen Punkte und n = N - 1

Dies kann man nun umformen in:

M^-1 * P = F

Wobei:

M^-1 ... die inverse von M ist

Dadurch erhält man alle Werte Fy die man benötigt und kann somit für ein gegebenes t wiederum in die allgemeine Form:

 I = (t^n)*Fn + (t^(n-1))*F(n-1) + ... + t*F1 + F0

einsetzen.

Rechenbeispiel

Wir wollen über 4 Punkte eine Polynominterpolation im 2 dimensionalen Raum. Diese sind:

P0: (5|3)
P1: (1|4)
P2: (4|2)
P3: (1|2)

Wir legen nun zuerst wieder die t-Werte für die Punkte fest, und sagen:

P0 bei t=0
P1 bei t=1/3
P2 bei t=2/3
P3 bei t=1

Und berechnen uns nun die Matrix M mit diesen t-Werten:

    |   0^3    0^2   0^1 1 |
M = | 0.33^3 0.33^2 0.33 1 |
    | 0.66^3 0.66^2 0.66 1 |
    |   1^3    1^2   1^1 1 |

Und berechnen uns nun die inverse M^-1:

       | -4.5  13.5 -13.5  4.5 |
M^-1 = |   9  -22.5   18  -4.5 |
       | -5.5   9    -4.5   1  |
       |   1    0      0    0  |

Nun nehmen wir den P-Vektor der ersten Dimension:

Px = (5|1|4|1)

und multiplizieren ihn mit der Matrix wodurch wir

Fx = M^-1 * Px = (-58.5|90|35.5|5)

erhalten. Nun das selbe für die zweite Dimension:

Py = (3|4|2|2)

und wiederum

Fy = M^-1 * Py = (22.5|-36|12.5|3)

Somit ist unsere endgültige Formel für die Interpolation:

Ix = -58.5 * t^3 + 90 * t^2 - 35.5 * t + 5
Iy = 22.5 * t^3 - 36 * t^2 + 12.5 * t + 3

Das Ergebnis sieht nun folgendermaßen aus:

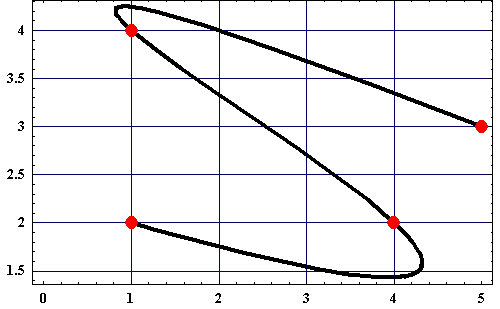
Oben angegebenes Beispiel grafisch dargestellt. Die Punkte P0 bis P3 sind rot dargestellt. Die Kurve beinhaltet alle Punkte der gegebenen Funktionen für ( Ix , Iy ) mit t im Wertebereich [0|1].

Kurven mit gegebenen Tangenten

Wir haben die oben gegebene Polynom-Gleichung für N Punkte. Wenn wir nun zusätzlich J Tangenten angeben möchten, so haben wir natürlich J zusätzliche Gleichungen und benötigen ein Polynom (N+K-1)ten Grades. Als erstes stellen wir wiederum eine derartige Polynom-Gleichung auf, jedoch mit dem Unterschied das wir dies gleich mit dem (N+J-1)ten Grad machen. Des weiteren müssen wir für jede Tangente Festlegen bei welchem t^x wir sie einbrigen möchten. Der Einfachheit halber wird hier die Reihung: zuerst die Punkte (also einem t^x mit höherem x) und danach die Tangenten (also einem t^x mit niedrigerem x als die Punkte bis hin zu x=0) verwendet. Daraus ergibt sich die allgemeine Form für die Punkte:

P0 = t(P0)^(n+J) * F(n+J) + t(P0)^(n+J-1) * F(n+J) + ... + t(P0)^(J+1) * F(J+1) + t(P0)^J * F(J) + t(P0)^(J-1) * F(J-1) + t(P0)^(J-2) * F(J-2) + ... + t(P0) * F1 + F0
P1 = t(P1)^(n+J) * F(n+J) + t(P1)^(n+J-1) * F(n+J) + ... + t(P1)^(J+1) * F(J+1) + t(P1)^J * F(J) + t(P1)^(J-1) * F(J-1) + t(P1)^(J-2) * F(J-2) + ... + t(P1) * F1 + F0
...
Pn = t(Pn)^(n+J) * F(n+J) + t(Pn)^(n+J-1) * F(n+J) + ... + t(Pn)^(J+1) * F(J+1) + t(Pn)^J * F(J) + t(Pn)^(J-1) * F(J-1) + t(Pn)^(J-2) * F(J-2) + ... + t(Pn) * F1 + F0

Wobei:

Px ... der x-te Punkt
t(Px) ... der t-Wert für den x-ten Punkt
F(n+J) bis F(J) ... der zu berechnende Faktor für den (N-1)ten Punkt
F(J-1) bis F(0) ... der zu berechnende Faktor für die J-te Tangente

Nun benötigen wir natürlich noch weitere Gleichungen für die Tangenten um das Gleichungssystem eindeutig lösbar zu machen. Eine Tangente K (hier wird bewusst K und nicht T gewählt) für den Xten Punkt lässt sich durch eine Ableitung nach t berechnen:

K(Px) = (n+J) * t(Px)^(n+J-1) * F(n+J) + (n+J-1) * t(Px)^(n+J-2) * F(n+J-1) + ... + (J+1) * t(Px)^(J) * F(J+1) + J * t(Px)^(J-1) * F(J) + (J-1) * t(Px)^(J-2) * F(J-1) + (J-2) * t(Px)^(J-3) * F(J-2) + ... + t(Px) * F2 + F1 + ( 0 * F0 )

Mit diesen Gleichungssystemen können wir wiederum eine Matrix formen, diese invertieren und los legen. Aber (meines Erachtens) erklärt sich dies am besten an einem Beispiel.

Hermite Kurven

Hermite Kurven sind Interpolationsfunktionen wo der Anfangs- und Endpunkt eine bestimmte Tangente aufweist. Üblicherweise werden Hermite Kurven zusätzlich noch auf 2 gegebene Punkte beschränkt, was wir hier der Einfachheit halber beibehalten wollen. Wir haben 2 Punkte, 2 Tangenten wodurch wir auf ein Polynom (N+J-1) = (2+2-1) = 3ten Grades kommen. Alse stellen wir eine Polynomgleichung für 2 gegebene Punkte auf, wobei der erste Punkt den Zeitpunkt 0 und der zweite Punkt den Zeitpunkt 1 erhält. Dadurch kommen wir auf zwei triviale Gleichungen:

P0 = 0 * F(3) + 0 * F(2) + 0 * F(1) + 1 * F(0)
P1 = 1 * F(3) + 1 * F(2) + 1 * F(1) + 1 * F(0)

Nun noch die Tangentengleichungen die sich aus der oben angegebenen K(Px) - Formel ergeben:

K0 = 0 * F(3) + 0 * F(2) + 1 * F(1) + 0 * F(0)
K1 = 3 * F(3) + 2 * F(2) + 1 * F(1) + 0 * F(0)

Dies ist unser lineares Gleichungssystem woraus wir wiederum unsere Matrix gewinnen:

    | 0 0 0 1 |
M = | 1 1 1 1 |
    | 0 0 1 0 |
    | 3 2 1 0 |

Und natürlich die Formel:

W = M * F

Wobei:

W ... ein Vektor ist der die Werte P0, P1, K0, K1 (in dieser Reihenfolge) beinhaltet
M ... die oben gegebene Matrix
F ... der Vektor der die zu berechnenden Werte beinhaltet.

Diese Matrix invertiert ergibt:

       |  2 -2  1  1 |
M^-1 = | -3  3 -2 -1 |
       |  0  0  1  0 |
       |  1  0  0  0 |

Somit können wir den F-Vektor berechnen durch

M^-1 * W = F

Wenn wir nun also für W die Werte (2,3,-1,1) hätten, wobei hier

2 ... der erste Punkt
3 ... der zweite Punkt
-1 ... die Tangente für den ersten Punkt
1 ... die Tangente für den zweiten Punkt

so ergeben sich daraus die Faktoren:

F = M^-1 * W = (-2,4,-1,2)

Wodruch wir für unsere Kurve folgende Formel erhalten:

f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2

Da die Dimensionen hier ebenfalls unabhängig sind, können Hermit-Kurven auf beliebig viele Dimensionen erweitert werden.

Das Ergebnis sieht nun folgendermaßen aus:

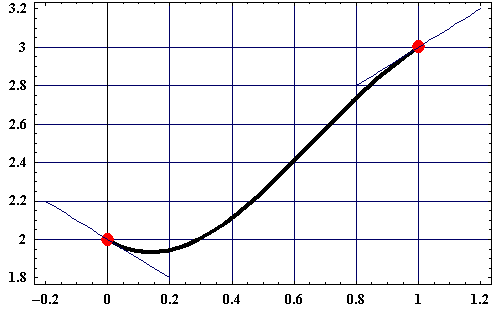
Oben angegebenes Beispiel grafisch dargestellt. Die beiden Punkte sind rot dargestellt, die beiden Tangenten sind als blaue Geraden eingezeichnet. Die Kurve beinhaltet alle Punkte der gegebenen Funktionen für t im Wertebereich [0|1].

Tangenten von Kurven

Besitzt man die Funktion für eine Kurve so lässt sich die Tangente durch das differenzieren dieser Funktion ermitteln. Aus unserem vorigen Beispiel wäre dies:

f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2
f'(t) = -6 * t^2 + 8 * t - t

Da die Dimensionen einer derartigen Kurve wie gesagt unabhängig voneinander behandelt werden können, kann man dadurch die Tangente in der entsprechenden Dimension erhalten.

Interpolation mit anderen Funktionen

Bisher wurden nur Interpolationen gezeigt, bei denen der t-Wert potenziert wurde. Es wurde immer ein Anfangspunkt verwendet, für den der t-Wert 0 sein sollte, und ein Endpunkt für den der t-Wert 1 sein sollte. Wir können natürlich jede beliebige Funktion für die Interpolation verwenden wo dies zutrifft. Wenn wir möchten können wir natürlich auch eine Funktion verwenden wo der Anfangspunkt bei t=X und der Endpunkt bei t=Y zu finden ist, denn eine derartige Funktion können wir wiederum umformen zu einer Funktion für die wir einen Anfangspunkt mit t=0 und einen Endpunkt mit t=1 haben.

Andere Funktionen werden meistens (nicht immer) bei nur 2 gegebenen Punkten verwendet. Hier wird meistens aus einem t-Wert im Bereich [0|1] ein neuer Wert u im Bereich [1|0] berechnet, welcher danach ähnlich wie bei der linearen Interpolation verwendet wird. Also:

u = f(t)
Interpolierter_Wert = I(t) = u * Startwert + (1-u) * Endwert

Wobei:

f(t) ... die Interpolationsfunktion, welche bei t=0 1 zurück liefert und bei t=1 0 ist.
Interpolierter_Wert ... das Ergebnis.

Mögliche andere Funktionen sind nun beispielsweise:

Cosinus ähnliche Interpolation

Cosinus Interpolation

Der Cosinus liefert Werte zwischen -1 und 1. Wir wollen einen eindeutigen y-Wert für y=Cos(t), somit verwenden wir nur t-Werte im Wertebereich von 0 bis 180 Grad (bzw. 0 bis Pi Radianten), denn bei t=181 Grad würden wir ja den selben Wert erhalten wie für t=179 Grad.

Der t-Wert wird für den Cosinus im Wertebereich [0|Pi] bzw. [0|180Grad] benötigt. Um nun einen t-Wert (wie zuvor) im Wertebereicheich von [0|1] verwenden zu können, multiplizieren wir ihn einfach mit Pi. Also verwenden wir einfach

t2 = t * Pi

bzw. das Ganze mit Grad:

t2 = t * 180

Der Ausgabewert von Cosinus ist im Wertebereich [1|-1]. Um ihn auf den Wertebereich [1|0] zu bringen, müssen wir ihn transformieren. Dafür formen wir um:

f(t2) = Cos(t2)
g(t2) = f(t2)/2 + 1/2 = ( 1 + f(t2) ) / 2 = ( 1 + Cos(t2) ) / 2

Und nun noch t2 durch t ersetzt:

g(t) = ( 1 + Cos(t*Pi) ) / 2

bzw. das Ganze mit Grad:

g(t) = ( 1 + Cos(t*180) ) / 2

Wir haben nun eine Formel die uns bei t=0 einen Wert von 1 liefert und bei t=1 einen Wert von 0. Dies können wir in unsere allgemeine Funktion einsetzen:

Interpolierter_Wert = I(t) = g(t) * Startwert + ( 1 - g(t) ) * Endwert

Und für g(t) eingesetzt:

Interpolierter_Wert = I(t) = ( (1+Cos(t*Pi))/2 ) * Startwert + ( 1 - (1+Cos(t*Pi))/2 ) * Endwert

bzw. das Ganze mit Grad:

Interpolierter_Wert = I(t) = ( (1+Cos(t*180))/2 ) * Startwert + ( 1 - (1+Cos(t*180))/2 ) * Endwert

Nun die Frage warum der ganze Aufwand, also warum nicht linear interpolieren? Um dies zu beantworten müssen wir die Steigungen dieser Funktion betrachten, wofür wir die Ableitung der Funktion berechnen:

I'(t) = 1/2 * Endwert * Pi * Sin( t * Pi ) - 1/2 * Startwert * Pi * Sin( t * Pi )

Sieht kompliziert aus, aber wenn wir nun t=0 annehmen so erhalten wir für Sin( t * Pi ) ebenfalls 0. Wenn wir für t=1 annehmen so erhalten wir für Sin( t * Pi ) wiederum 0. Und dadurch erhalten wir an beiden Enden eine Steigung von 0.

Was können wir machen mit einer Funktion die an beiden Enden eine Steigung von 0 aufweist? Ganz einfach: wir können mehrere dieser Funktionen aneinander reihen, ohne das man einen übergang erkennt. Somit können wir sagen:

Bei t im Bereich [0|1] verwende als Startwert 3 und als Endwert 1
Bei t im Bereich ]1|2] verwende als Startwert 1 und als Endwert 7
Bei t im Bereich ]2|3] verwende als Startwert 7 und als Endwert 8

Und wenn wir alle 3 Funktionen mit dem Wertebereich [0|1] verwenden (oder mathematisch ausgedrückt: I2(t) = I(t modulo 1) ), so erhalten wir eine Kurve ohne Kanten, oder um es etwas mathematischer auszudrücken: diese Funktion ist im Wertebereich ]0|3[ ableitbar, also in diesem Wertebereich auch stetig.

Quadratische Annäherung der Cosinus Interpolation

Da die Berechnung des Cosinus eine etwas aufwändigere Angelegenheit ist, wünscht man sich hin und wieder eine Funktion die ähnlich aussieht und die gleichen Bedingungen (also eine Steigung von 0 an Start- und Endpunkt) erfüllt. Hierfür kann man 2 quadratische Funktionen verwenden die folgendes erfüllen müssen:

1. Beide Kurven müssen einen gemeinsamen Punkt besitzen, also I1(t) = I2(t) für t im Wertebereich [0|1]
2. An diesem Punkt müssen beide Kurven die selbe Steigung besitzen, also es existiert ein ( I1(X) = I2(X) wo auch gilt I1'(X) = I2'(X) ).
3. Steigung (also Ableitung) bei t=0 und t=1 soll 0 sein
4. Die Kurve sollte symmetrisch sein bezogen auf t=0.5, so das gilt: I1(t) = 1-I2(1-t). Somit muss gleichzeitig der Punkt wo gilt I1(t) = I2(t) bei 0.5 liegen.

Wir können uns nun aus der ersten und dritten Bedinung einfach die beiden Formeln herleiten, aber um es kurz zu machen:

Wenn t <= 0.5 dann I1(t) = -2*t^2 + 1
Wenn t > 0.5 dann I2(t) = 2*t^2 - 4*t + 2 = 2 * (1-t)^2

Nun zeigen wir, dass die oben angegebenen Bedingungen erfüllt sind:

1. I1(0.5) = -2*0.5^2 + 1 = 0.5; I2(0.5) = 2 * (1-0.5)^2) = 0.5
2. I1'(t) = -4t, I1'(0.5) = -2; I2'(t) = 4*t - 4, I2'(0.5) = -2
3. I1'(0) = -4*0 = 0; I2'(1) = 4*1 - 4) = 0
4. I1(t) = 1-I2(1-t) => -2*t^2 + 1 = 1 - (2*(1-t)^2 - 4*(1-t) + 2) => -2*t^2 + 1 = 1 - (2 - 4*t + 2*t^2 - 4 + 4*t + 2) => -2*t^2 + 1 = -2*t^2 + 1

Cosinus ähnliche Interpolation durch Polynominterpolation

Wenn wir eine Polynominterpolation mit den beiden Endtangenten 0 berechnen wollen, so verwenden wir eine Hermite Kurve. Hierbei verwenden wir die Werte:

1 ... Startpunkt
0 ... Endpunkt
0 ... Steigung bei Startpunkt
0 ... Steigung bei Endpunkt

Mit der unter Hermit Kurven angegebenen Matrix M^-1 können wir uns nun die dazugehörige Funktion berechnen und erhalten:

I(t) = 2*t^3 - 3*t^2 + 1

Die ersten beiden Bedingungen von vorher sind automatisch erfüllt, da es sich nur um eine Funktion handelt. Für die 3. und 4. Bedingung lässt sich ebenfalls verhältnismäßig einfach zeigen das sie erfüllt sind.

Vergleich der Cosinus ähnlichen Interpolationsarten

Und zu guter letzt hier noch die grafische Veranschaulichung der etwas zahlenbeladenen Funktionen.

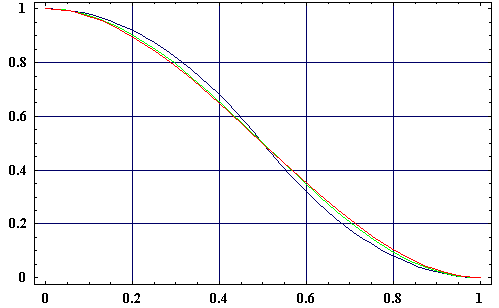
Die 3 Cosinus ähnlichen Funktionen graphisch dargestellt:

• Grün: Cos-Interpolation
• Rot: Polynom-Interpolation
• Blau: Quadratische Annäherung

Interpolierte Flächen

Bisher wurden ausschließlich Kurven betrachtet. Aus Kurven lassen sich jedoch ohne größere Umstände auch Flächen bilden. Hier hat man zwei (unterschiedliche) t-Werte und eine Matrix von Punkten gegeben, wobei jeder Punkt gegebenenfalls noch 1 oder 2 Tangenten besitzen kann. Um einen Punkt einer Fläche zu berechnen interpoliert man zuerst die Punkte für jede Zeile der Punktmatrix. Nachdem man nun die interpolierten Punkte für jede Zeile besitzt kann man sich mit diesen Punkten ein neues Gleichungssystem aufstellen und wiederum eine Kurve bilden. Diese Kurve interpoliert man wiederum mit dem zweiten gegebenen t-Wert. Dies lässt sich auf beliebig viele Dimensionen nach dem gleichen Schema erweitern, üblicherweise wird dies jedoch nur für Oberflächen (also 2D) benötigt.

Normalvektoren

Besitzt man Flächen und berechnet sie nach dem gegebenen Schema, so berechnet man sich zuerst auch mehrere Kurven von denen man die Tangenten berechnen kann. Interpoliert man nun diese Tangenten mit der gleichen Kurvenfunktion wie die resultierenden Punkte, und berechnet sich aus der resultierenden Kurvenfunktion ebenfalls die Tangente, so erhält man 2 Tangenten. Aus diesen beiden Tangenten kann nun mit einem Kreuzprodukt ein Normalvektor errechnet werden.
ACHTUNG: auf Richtigkeit überprüfen

Kurvenlängen-Interpolation

Es könnte erwünscht sein (beispielsweise für Kamerafahrten, Keyframe Interpolationen jeglicher Art oder auch bei der Interpolation von Positionsangaben die man beispielsweise über ein Netzwerk erhält), dass man über keine fixe Achse t interpolieren möchte, sondern über die Kurvenlänge. Die Kurvenlänge kann man sich hierbei als den tatsächlich zurückgelegten Weg vorstellen. Die Länge einer Kurve f bis zu einem Punkt t im Bereich [0,1] wird berechnet durch:

Länge(t) = Integral[0 bis t]( f'(t) )

Wenn man nun eine bestimmte Kurvenlänge s finden möchte, dann muss man den dazugehörigen Wert t finden wo gilt Länge(t)- s = 0. Da es genau einen Wert t gibt auf den dies zutrifft kann dies beispielsweise durch das Newtonsche Näherungsverfahren erreicht werden, welches in wenigen Iterationsschritten eine sehr präziese Lösung liefert.
ACHTUNG: auf Richtigkeit überprüfen