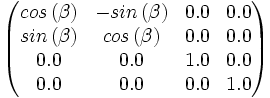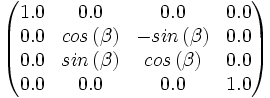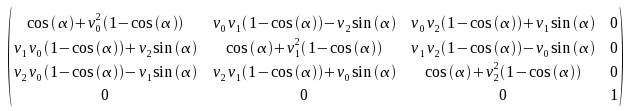Tutorial OpenGL3 Lineare Algebra

Rotate

Das Bewegen auf den 3 Achsen ist allerdings oft nicht ausreichend und deswegen gibt es auch eine Rortations-Matrix. Die Rotations-Matrix wird durch 3 Vektoren beschrieben, welche jeweils für die x,y und z Achse zuständig sind. Man kann die Rotation, der einzelnen Achsen in einem Schritt oder in 3 einzelne Aufteilen. Um die Rotationsmatrix besser zu verstehen werden erst einmal alle Achsen einzeln betrachtet.

Drehen um die Z-Achse

Der Z-Achsen Einheitsvektor(3. Spalte=0.0, 0.0, 1.0, 0.0) bleibt bei der Rotation unverändert - man nehme einen Finger, deute damit nach vorne. Nun drehe man diesen Finger um seine eigene Achse, wohin zeigt er? In die selbe Richtung wie vor der Drehung? Damit entspricht Z-Achsen Einheitsvektor auch der vorletzen Spalte der Matrix: (0.0, 0.0, 1.0, 0.0)

Der X-Achsen Einheitsvektor(1. Spalte=1.0, 0.0, 0.0 0.0) dreht sich hingegen mit. Trigonometrie findet der Lösung Spur. Ein Blick auf das Bild zum Einheitskreis zeigt, dass wir gerade das gleiche Problem für X und Y zu bewältigen haben: Die Rotationsachse ist in beiden Fällen die Z-Achse. Der Einheitsvektor, der gedreht wird, ist der X-Achsen Einheitsvektor also:

x = cos(ß)
y = sin(ß)

womit der Inhalt der ersten Spalte der Matrix kennen: (cos(ß), sin(ß), 0.0, 0.0)

Dies kann man auch auf den Y-Achsen Einheitsvektor(2. Spalte=0.0, 1.0, 0.0, 0.0) übertragen, man muss nur bedenken in welcher weise sich x und y vertauschen:

x = -sin(ß)
y = cos(ß)

So ergibt sich für die zweite Spalte: (-sin(ß), cos(ß), 0.0, 0.0)

Nun kann man die Rotationsmatrix für die Rotation auf der Z-Achse beschreiben, die Matrix findet man am Anfang des Abschnittes.

Drehen um die Y-Achse

Die Berechnung der Matrix wird auf die gleiche weise ermittelt, wie bei der Berechnung der Z-Achsen Rotationsmatrix.

Drehen um die X-Achse

Rotation um alle Achsen mit einer Matrix

Es ist recht aufwändig für die CPU und für den Programmierer immer 3 Rotationen aus zu führen, deswegen hat man diese auch zu einer einzigen Operation zusammen gefasst. Die Matrizen werden einfach miteinander multipliziert und es kommt eine Rotationsmatrix herraus, welche 3 Eingabeparameter benötigt, alpha, beta und gamma sind dabei die Winkel für X-,Y- und Z-Achse.

Eine weitere Möglichkeit, um eine Rotationsmatrix zu erstellen, wäre das nutzen eines Richtungsvektors und einem Winkel. Hierbei wird der Winkel auf den Richtungsvektor angewendet, wenn also man als Vektor (1,0,0) verwendet dann hat man eine Rotation auf der X-Achse, (0,1,0) Y-Achse und (0,0,1) für die Z-Achse. Man kann nun auch Vektoren wie (1,1,1) angeben, wobei die Funktion diesen Vektor dann normalisieren wird, damit er noch auf das Einheitskreis System funktioniert. Dieser Vektor ist nicht equivalent mit dem Rotieren von X-,Y- und Z-Achse nacheinander. Der Vorteil hierbei liegt in der Kompaktheitund des Codes und man kann auf Algorithmen zurück greifen, die vor OpenGL3 entwickelt wurden, da der OpenGL Treiber früher die Rotation über diese Variante Implementiert hatte.

    void Rotate(T w,T x,T y,T z)
    {
      TKar_Matrix<KAR_MATH_TYPE> m;
      T rad=TKar_Math<T>::DegToRad(w);
      T c=TKar_Math<T>::Cos(rad);
      T ic=1.0-c;
      T s=TKar_Math<T>::Sin(rad);
      TKar_Vector<T> v(x,y,z,0.0);
      T mag=TKar_Math<T>::Sqrt((v*v).Sum());

      if (mag<=1.0e-4)
        return;

      v[0]=x/mag;
      v[1]=y/mag;
      v[2]=z/mag;

      m[0][0]=(v[0]*v[0]*ic)+c;
      m[0][1]=(v[0]*v[1]*ic)+(v[2]*s);
      m[0][2]=(v[0]*v[2]*ic)-(v[1]*s);

      m[1][0]=(v[0]*v[1]*ic)-(v[2]*s);
      m[1][1]=(v[1]*v[1]*ic)+c;
      m[1][2]=(v[1]*v[2]*ic)+(v[0]*s);

      m[2][0]=(v[0]*v[2]*ic)+(v[1]*s);
      m[2][1]=(v[1]*v[2]*ic)-(v[0]*s);
      m[2][2]=(v[2]*v[2]*ic)+c;

      *this*=m;
    }