Tutorial Vertexprogramme

VertexProgramme - Weg von der festen Funktionspipeline hin zur frei programmierbaren GPU

Ave!

Und erstmal willkommen zu meinen vierten Tut, in dem wir uns einer etwas fortgeschrittenen Technik, den Vertexprogrammen (unter Direct3D auch VertexShader) genannt widmen.Alle die bereits mit den grundlegenden Funktionen OpenGLs wie z. B. Texturemapping oder dem übergeben von Vertexdaten Probleme haben, sollten sich dieses Tutorial für einen späteren Zeitpunkt aufheben, denn es geht etwas über die Standard-OpenGL-Thematik hinaus. Weiterhin wären auch einige Grundkenntnisse in Sachen Assembler nicht schlecht, da Vertexprogramme in einer Assemblersprache (jedoch mit auf die GPU angepassten Tokens) geschrieben werden.Deshalb wäre es von Vorteil wenn man in seinem Leben schon mal in irgendeiner Form Assembler programmiert hat, egal ob dies auf der x86, x85 oder gar der Motorola-Chipgeneration war.

Einleitung

Lange Zeit ging es den Entwicklern neuer Grafikchips nur um die Erhöhung der Geschwindigkeit in Form von höheren Füllraten und besseren Polygondurchsätzen (wie u. a. die feste T&L-Einheit von nVidias GeForce).Doch schnell wurde bemerkt, das es nicht nur die Erhöhung der Geschwindigkeit alleine bringt, sondern neue Features zur Verbesserung der Grafiken her mussten, die den Entwicklern mehr Freiheit im Bezug auf die Programmierung des Grafikchips bieten sollten.

nVidia führte dann als erste Chipschmiede über die NV_VERTEX_PROGRAM-Erweiterung (GeForce1/2 ab Detonator40, GeForce3/4/FX nativ) die Möglichkeit ein, die feste Funktionspipeline (festverdrahtete HW T&L-Einheit bei GF1/2, ab GF3 wird diese sowieso über VertexProgramme emuliert) zu umgehen und mittels einer assemblerähnlichen Sprache eigene Operationen mit den Vertexen auszuführen. ATI konterten ihrerseits bei der Einführung der Radeon8500 im Zuge ihrer neuen Smartshader-Technologie mit der GL_EXT_VERTEX_SHADER-Erweiterung, die in etwa der von nVidia vorgestellten Lösung entsprach.Allerdings war an der Namensgebung bereits erkennbar das diese Erweiterung in eine neue OpenGL-Version herstellerunabhängig einfliessen sollte (Allerdings übernahm das OpenGL-ARB dann doch die nVidia-Erweiterung und erweiterte diese bei der Übernahme in den ARB-Standard).

Zu diesem Zeitpunkt war es also "endlich" möglich direkt in die Renderpipeline von OpenGL einzugreifen.Das Problem war allerdings (wie schon so oft) die Tatsache das es mal wieder zwei herstellerabhängige Extensions gab, und man so wieder gezwungen je nach verwendeter GPU andere Renderpfade zu nutzen, was ja gegen die Grundsätze OpenGLs spricht.

Mit der Einführung von OpenGL 1.4 am 24.Juli 2002 wurde diesem herstellerspezifischem Treiben dann mittels der GL_ARB_VERTEX_PROGRAM-Erweiterung endlich ein Ende gesetzt, so dass der Verwendung von Vertexprogrammen eigentlich (bis auf die Hardwarevorraussetzungen) seither nichts mehr im Wege steht.

Leider siehts in Sachen Tutorials und Dokumentation (bis auf die Spezifikationen der Erweiterung) zur neuen ARB-Erweiterung mehr als dürftig aus (von deutschsprachigen Dokumenten wollen wir erst gar nicht reden), weshalb ich mir die Mühe gemacht habe ein recht ausführliches Tutorial zu schreiben, das auch gleichzeitig als Nachschlagewerk für die verschiedenen Attributregister und Statusvariablen dienen soll... ich hoffe damit auch den ein oder anderen vor allem von nVidias-Vertexprogrammen wegzubringen, da deren Erweiterungen trotz dieser neuen, herstellerunabhängigen, noch sehr oft genutzt wird.

Auch wenn die Materie in den nächsten Kapiteln manchmal recht trocken wirken kann, wünsche ich euch dennoch viel Spaß beim Lesen, und vor allem beim Umsetzen des Gelernten!

Hardwareunterstützung

Damit ihr euch beim Schreiben eurer Vertexprogramme keine Sorgen um Kompatibilität machen müsst, gibts hier eine kleine Tabelle in der alle wichtigen Grafikchips vertreten sind, die mindestens eine VertexProgramm/Shader-Erweiterung unterstützen.Wie gut zu erkennen, unterstützen von den modernen Grafikboliden bis auf die Matrox Pharelia alle die neue ARB_VERTEX_PROGRAM-Erweiterung.Diese Karte sollte das allerdings mit einem neuen Treiber auch tun (momentanter Treiberstand liegt noch bei OpenGL 1.3). Aufpassen müsst ihr bei den GeForce1/2-Karten, die einige Extensions erst ab einem bestimmten Treiberrelease unterstützen und dies dann auch nur per Software (also recht langsam).

Um euch im Bezug auf die Unterstützung dieser Extension auf den verschiedenen Grafikkarten auf dem Laufenden zu halten, empfehle ich euch übrigens den entsprechenden Eintrag aus Tom Nuydens OpenGL-Hardwareregistry.

Vertexprogramm-Unterstützung

GPU	EXT_vertex_shader	NV_vertex_program	ARB_vertex_program
Radeon8500
Radeon9000/9100/9200
Radeon9500/9700/9800
Matrox Parhelia
GeForce1		Ab Detonator 10	Ab Detonator 40
GeForce2			Ab Detonator 40
GeForce3/4
GeForceFX
SiS Xabre

Vertexprogramme in der Renderpipeline

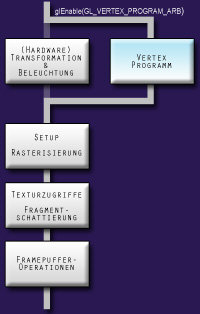
Auf dem Diagramm zu unsrer Linken sehen wir die Renderpipeline, die beim Rendern einer (OpenGL)Szene durchlaufen wird. Im linken Pfad ist die fest verdrahtete (HW)T&L-Einheit zu sehen, durch die alle Vertexe hindurchgejagt werden, bevor diese dann an den Rasterisierer weitergereicht werden. So war es vor der Einführung von Vertexprogrammen.

Rechts der T&L-Stufe sehen wird jedoch einen neuen Teilpfad, das Vertexprogramm. Dieser wird nach aktivieren eines Vertexprogrammes via glEnable(GL_VERTEX_PROGRAM_ARB) durchlaufen, umgeht somit die feste (HW)T&L-Einheit und lässt uns unsere eigenen per-Vertex-Operationen in einem Vertexprogramm auf der GPU durchführen.

Durch die Umgehung der T&L-Einheit bieten sich dem Grafikprogrammierer nun jede Menge neuer Manipulationsmöglichkeiten:

• Komplette Kontrolle über Transformation und Beleuchtung der Vertexe
• Eigene Beleuchtungsmethoden (per Vertex)
• Eigene per-Vertex Berechnungen
• Eigene Texturkoordinatengeneration
• Eigene Texturenmatrixoperationen
• Eigene Berechnung von Nebelkoordinaten
• uvm.

Und das geschieht natürlich alles hardwarebeschleunigt und auf der GPU, so dass die CPU durch Vertexprogramme je nach Fall stark entlastet werden kann und so mehr Zeit für KI-Berechnungen oder Kollisionsabfragen hat.

Was ist ein Vertexprogramm?

Bevor wir uns also näher mit der verwendeten Assemblersprache beschäftigen, gibts noch eine kurze Begriffserklärung um den Begriff Vertexprogramm ins richtige Licht zu rücken. Wie schon angesprochen basieren Vertexprogramme auf einer assemblerähnlichen Sprache, die mit 27 GPU-angepassten Befehlen daherkommt, und bietet die Möglichkeit Vertexe zu manupilieren.Dies bedeutet, das man EIN Vertex vorne reingibt, und dann am Ende EIN manipuliertes Vertex herausbekommt. Es ist also nicht möglich in einem VP neue Vertexe zu generieren oder vorhandene zu löschen, und es gibt auch keine Möglichkeit topologische Informationen wie z. B. Nachbarbezüge an ein VP zu übergeben.

Folgende Funktionen werden vom VP umgangen und können (müssen) selbst implementiert werden:

• Modelansichts und Projectionsvertextransformationen
• Vertexgewichtung/Blending
• Normalentransformation, Reskalierung und Normalisierung
• Farbmaterialien
• Per-Vertex Beleuchtung
• Generierung von Texturenkoordinaten
• Transformationen der Texturenmatrix
• Per-Vertex Punktgröße
• Berechnung von Nebelkoordinaten
• Benutzerdefinierte Schnittflächen

Was bedeutet das nun? Kurz und schmerzlos: Alle oben genannten Funktionen der T&L-Einheit die wir in unserem Programm nutzen wollen müssen wir von Hand über unser Vertexprogramm realisieren.Wenn man in seiner Anwendung z. B. Nebel nutzen will, und dies wie gewohnt über OpenGLs Funktionen macht, dann wird dies bei der Nutzung eines Vertexprogrammes erstmal kein sichtbares Ergebnis bringen.Aber keine Angst, denn in einem solchen Falle (sprich wenn ihr nicht selbst irgendwelche komplexen Nebelberechnungen durchführen wollt), dann reicht es wenn ihr dann die Nebelkoordinaten einfach durchschleift (dazu später mehr).

Folgende Funktionen werden vom VP nicht verändert, und können über ein solches auch nicht manipuliert werden:

• Evaluatoren
• Clipping gegen das Ansichtsfrustum
• Perspektivendivision
• Viewporttransformationen
• Tiefentransformationen
• Zusammensetzung der Primitiven
• Rasterisierung
• Blending

Vertexprogramm einbinden

Um die Nutzung von Vertexprogrammen recht einfach zu gestalten, hat man sich bei der Entwicklung der neuen Befehle stark an die bereits vorhandene Terminologie bei der Verwendung von Texturobjekten gehalten, so dass Erstellung und Nutzung von VPs einfach von Hand gehen.

Folgende Befehle wurden mit OpenGL1.4 deshalb implementiert:

glGenProgramsARB(n : TGLsizei; programs : PGLuint)

Erstellt unter dem Zeiger programs Platz für n Vertexprogramme.

glBindProgramARB(target : TGLenum;aprogram : TGLuint)

Schaltet zum in aprogram angegebenen Vertexprogramm um, target muss hier gleich GL_VERTEX_PROGRAM_ARB sein.

glGetProgramStringARB(target : TGLenum;pname : TGLenum;astring : PChar)

Bindet das in astring angegebene Programm an das aktuell gebundenen Vertexprogramm. target muss hier auch wieder GL_VERTEX_PROGRAM_ARB sein, und der Parameter pname gibt das Format des in astring übergebenen Programmes an. Im Normalfall (wenn das VP z. B. aus einer externen Datei geladen wird), ist dieser Parameter gleich GL_PROGRAM_FORMAT_ASCII_ARB zu setzen.

Folgender Codeschnippsel zum Laden eines Vertexprogrammes zeigt, wie einfach deren Nutzung durch die neue Erweiterung und die an Texturobjekte angelehnten neuen Funktionen ist:

      var
       VPString : TStringList;
      [...]
      // Vertexprogram aus der Datei laden (einfache Textdatei)
      VPString := TStringList.Create;
      VPString.LoadFromFile(pFileName);
      // Vertexprogramme aktiveren
      glEnable(GL_VERTEX_PROGRAM_ARB);
      // Speicherplatz für das Vertexprogramm reservieren
      glGenProgramsARB(1, @VertexProgram);
      // Vertexprogramm binden
      glBindProgramARB(GL_VERTEX_PROGRAM_ARB, VertexProgram);
      // Vertexprogramm kompilieren
      glProgramStringARB(GL_VERTEX_PROGRAM_ARB, GL_PROGRAM_FORMAT_ASCII_ARB, Length(VPString.Text), PChar(VPString.Text));
      VPString.Free;
      [...]

Vertexprogramm(ierung)

Da wir nun (hoffentlich) wissen wie wir Vertexprogramme in unsere Anwendung einbinden, werden wir uns nun in den nächsten Kapiteln mit den Elementen der assemblerähnlichen Sprache beschäftigen in der VPs programmiert werden.Wer schonmal Berührungen mit einer Assemblersprache hatte, der kann sich beruhigt zurücklehnen, denn Vertexprogramme sind weitaus weniger komplex, da es hier Dinge wie Sprünge oder Verzweigungen (noch) nicht gibt.

Wichtiger Hinweis für Delphianer: Genau wie bei C, muss auch bei der für Vertexprogramme genutzten Assemblersprache auf Groß- und Kleinschreibung geachtet werden. "Mov R1,R2" ist deswegen also ungültig, wohingegen "MOV R1,R2" korrekt ist!

Aufbau und Syntax eines Vertexprogrammes

Bevor wir uns in die Flut von Registern, Variablentypen und Befehlen werfen mit denen wir unsere Vertexe manipulieren könnten, wäre es erstmal eine gute Idee wenn wir uns mit dem Aufbau eines Vertexprogrammes und der Befehlssyntax anhand eines einfachen Beispiels beschäftigen. Stellen wir uns mal vor unser erstes Vertexprogramm sähe so aus:

!!ARBvp1.0
# Konstanten
PARAM ModelViewProj[4] = { state.matrix.mvp };
# Temporäre Variablen
TEMP temp;
# Hier werden alle Achsen in den Clipspace transformiert.Hier wird also nichts weiter getan  als das
# was OpenGL auch macht um die Vertexe korrekt auf dem Bildschirm zu platzieren
DP4 temp.x, ModelViewProj[0], vertex.position;
DP4 temp.y, ModelViewProj[1], vertex.position;
DP4 temp.z, ModelViewProj[2], vertex.position;
DP4 temp.w, ModelViewProj[3], vertex.position;
# Vertexposition ausgeben
MOV result.position, temp;
# Vertexfarben ausgeben
MOV result.color, vertex.color;
# Texturkoordinaten unverändert weitergeben
MOV result.texcoord, vertex.texcoord;
END

Das ist das minimalste Vertexprogramm das man schreiben kann (es sei denn man verzichtet auf Vertexfarben und Texturkoordinaten).Dieses VP macht nichts anderes, als das was die feste T&L-Einheit tun würde. Schauen wir uns die Programmteile aber erstmal Stück für Stück an:

!!ARBvp1.0

Dies ist das Headertoken welches am Anfang eines jeden Vertexprogrammes stehen muss und dieses einleitet. vp1.0 spiegelt hier die Version des VPs wieder. Da momentan aber nur Version 1.0 existiert, wird man hier auch nichts anderes finden.

PARAM ModelViewProj[4] = { state.matrix.mvp };

In dieser Zeile deklarieren wir eine Konstante als ein Array mit vier Werten (Im Gegensatz zu Delphi beginnt hier die Nummerierung bei 1 und nicht bei 0), der sofort die aktuelle Modelansichtsprojektion zugewiesen wird (dazu später mehr). Eine Konstantendeklaration beginnt immer mit dem Schlüsselwort PARAM, gefolgt vom Namen dieser Konstanten.Hinter dem Gleichheitszeichen folgt dann C-typisch die Angabe der Konstantenwerte in geschweiften Klammern. Dabei ist es (wie oben gemacht) nicht immer nötig die größe des Arrays hinter dem Variablennamen anzugeben. "PARAM a = {1,0,0,1}" ist deshalb genauso möglich (und gültig) wie "PARAM a[4] = {1,0,0,1}".

DP4 temp.x, ModelViewProj[0], vertex.position;
DP4 temp.y, ModelViewProj[1], vertex.position;
DP4 temp.z, ModelViewProj[2], vertex.position;
DP4 temp.w, ModelViewProj[3], vertex.position;

Was hier programmtechnisch gemacht wird, ist ja bereits aus obigem Kommentar ersichtlich.Wir berechnen die Position des Vertex auf dem Bildschirm, da OpenGL dies aufgrund der Umgehung der festen T&L-Einheit nicht mehr für uns tut. Worum es mir hier eher geht (die Erläuterung zu den verschiedenen Befehlen kommt später) ist die Erklärung der Syntax. Wer schonmal Assembler geproggt hat, der kann sich diesen Abschnitt sparen. Eine Assemblerinstruktion sieht immer wie folgt aus : Opcode dst, s0, [s1], [s2] [ ] = Optional OpCode ist der Befehl, dst entspricht dem Zielregister, während s0 bis s2 (wobei die Anzahl der Quellregister Befehlsabhängig ist) die Quellregister darstellen. Wie jedem der wenigstens ein paar EDV-Grundlagen hat bekannt ist, werden die Quellregister verknüpft (je nach Befehl verschieden) und dann ins Zielregister kopiert. Dies ist sehr wichtig für die Verständis, also behaltet das bitte immer im Hinterkopft! Oben zu erkennen ist übrigens die Angabe der Komponente hinter temp, mit deren Hilfe man festlegen kann in welchen Teil des Zielregisters geschrieben wird.Die anderen Koponenten bleiben dann unberührt. Auch das Tauschen von Komponenten ist so möglich.

Hier zum besseren Verständnis der Syntax ein paar Beispiele :

 MOV R1.x, R2;

Schreibt nur die x-Komponente von R2 in Register R1

 MOV R1.xz, R2;

Schreibt nur die x- und z-Komponente von R2 in R1

 MOV R1, R2.yzwx;

Neuer Inhalt von R1 = {R2.y, R2.z, R2.w, R2.x}

MOV result.position, temp;
MOV result.color, vertex.color;
MOV result.texcoord, vertex.texcoord;

Anhand obiger Erklärung solltet ihr jetzt ohne Prolem in der Lage sein, zu erkennen was diese Zeilen tun...ganz genau, sie geben die von uns genutzten Vertexattribute weiter. Die Sache mit der Vertexposition ist natürlich ein Muss, denn unser VP soll die veränderte Vertexposition ja weitergeben. In der zweiten Zeile geben wir dann auch die Vertexfarbe weiter. Würden wir das nicht tun, dann blieben evtl. Farbaufrufe via glColor3f in unserer Anwendung ohne Funktion. In der dritten Zeile werden dann auch noch die ans VP gelieferten Texturkoordinaten der Textureinheit 0 weitergeschleift. Natürlich ist dies bei Verwendung einer Textur unabdingbar.

END

Eigentlich kaum erwähnenswert, allerdings muss das END-Token am Ende des Vertexprogrammes stehen!

Unser Vertexprogramm "in Aktion" (welches jetzt noch nichts tut, was die übergangene T&L-Einheit nicht auch täte):

Fehlerprüfung

Natürlich kann der Delphicompiler unser selbstgeschriebenes Vertexprogramm nicht auf seine Korrektheit hin überprüfen, und da der Mensch gerne mal Fehler macht (der eine mehr, der andere weniger) wäre es keine schlechte Idee unser VP nach dem Laden auf eventuelle Fehler zu überprüfen. Dazu können wir uns glücklicherweise der OpenGL-Fehlererkennung mittels glGetError bedienen, die uns anhand des Rückgabewertes GL_INVALID_OPERATION nach der Programmübergabe durch glProgramStringARB auf einen Fehler in unserem Vertexprogramm hinweist.

Folgender Quellcode weist uns auf einen eventuellen Fehler und dessen Position im VP hin:

glProgramStringARB(...);
if glGetError = GL_INVALID_OPERATION then
 begin
 ErrorStr := glGetString(GL_PROGRAM_ERROR_STRING_ARB);
 ShowMessage(ErrorStr);
 Application.Terminate;
 end;

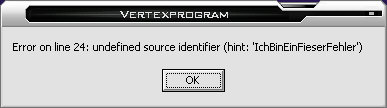
Wenn wir nun irgendwo in unserem VP einen Fehler gemacht haben, dann werden wir vom Grafiktreiber mit einem ähnlichen (dieser stammt von einer Radeon9700) Dialog "belohnt", der uns über unseren Fehler und dessen ungefähre Position informiert:

Programmgrenzen

Beim Schreiben von Vertexprogrammen gibt es nicht nur Grenzen bei der Anzahl der nutzbaren Variablen, sondern auch Begrenzungen im Bezug auf die Länge eines Vertexprogrammes.Diese variieren wieder von Implementation zu Implementation.

Die Anzahl der Instruktionen die man in einem VP nutzen kann, lässt sich mittels der Prozedur glGetProgramivARB und dem Token GL_MAX_PROGRAM_INSTRUCTIONS_ARB ermitteln. Während eine GeForce4 hier auf 128 Instruktionen limitiert ist, können Radeonkarten der 9x000er Serie seit dem Catalyst3.4-Treiber bis zu 65535 Instruktionen über einen F-Puffer realisieren, so dass man in der Länge seiner Vertexprogramme auf solchen Karten kaum limitiert ist.

Sollte die Länge eures VPs deshalb mal die maximale Anzahl der von der GL-Implementation verarbeitbaren Instruktionen überschreiten, bleibt euch nichts anderes übrig als diesen in zwei seperate VPs zu splitten und die Szene dann mit den zwei verschiedenen VPs in zwei (oder mehreren) Durchläufen zu zeichnen.Dies ist deshalb möglich, da unsere Vertexe nach dem Durchlaufen des VPs nicht direkt an den Rasterisierer (und somit auf den Schirm gebracht) werden, sondern nur deren im VP veränderte Eigenschaften gespeichert werden, und diese somit im nächsten Durchlauf wieder von einem anderen VP verändert werden können.

Kleiner Tipp am Rande : Wenn ihr in obiger Funktion das GL_MAX_PROGRAM_INSTRUCTIONS_ARB-Token durch GL_PROGRAM_INSTRUCTIONS_ARB ersetzt, liefert euch OpenGL die Anzahl der Instruktionen eures momentan aktiven Vertexprogrammes zurück.

Attributregister und Statebindings

Um dem Programmierer von Vertexprogrammen die Parameterübernahme aus dem Hauptprogramm stark zu vereinfachen (ein weiterer Grund wird wohl die je nach Implementation geringe Zahl der nutzbaren Parameter sein), wurden jede Menge Attribute und OpenGL-States über fest vorbelegte Variablennamen zugängig gemacht, in denen deren momentane Zustände abgelegt und zum Abruf bereit sind. Im folgenden Kapitel gibts daher zu allen Attribut- und Stategruppen eine handliche Tabelle und eine kurze Erklärung.

Vertex-Attribut-Register

Nachdem wir uns nun ein wenig mit der Syntax vertraut gemacht haben, widmen wir uns nun den im Vertexprogramm zur Verfügung stehenden, vordefinierten Registern und deren Bedeutung.Über diese festgelegten Register haben wir Zugriff auf fast alle erdenklichen Vertexattribute und OpenGl-States.

Beginnen wollen wir dann mal mit den Vertex-Attribut-Registern, über die wir Zugriff auf die von OpenGL an unser VP gesendeten Vertexe haben.

Attributregister	Komponenten	Bemerkung
vertex.position	x,y,z,w	Vertexposition
vertex.color	r,g,b,a	Primäre Farbe
vertex.color.primary	r,g,b,a	Primäre Farbe
vertex.color.secondary	r,g,b,a	Sekundäre Farbe
vertex.normal	x,y,z,1	Normale
vertex.fogcoord	f,0,0,1	Nebelkoordinate
vertex.texcoord	s,t,r,q	Texturkoordinate (Textureinheit 0)
vertex.texcoord[n]	s,t,r,q	Texturkoordinate (Textureinheit n)
vertex.matrixindex	i,i,i,i	Vertexmatrix Indizes 0-3
vertex.matrixindex[n]	i,i,i,i	Vertexmatrix Indizes n-n+3
vertex.weight	w,w,w,w	Vertexgewichtungen 0-3
vertex.weight[n]	w,w,w,w	Vertexgewichtungen n-n+3
vertex.attrib[n]	x,y,z,w	Generisches Vertexattribute n

Vertex-Ergebnis-Register

Um die im VP veränderten Vertexattribute wieder an OpenGL zu übergeben, stehen uns folgende Ergebnisregister zur Verfügung:

Ergebnisregister	Komponenten	Bemerkung
result.position	x,y,z,w	Position als Clipkoordinaten
result.color	r,g,b,a	Primäre Farbe der Vorderseite
result.color.primary	r,g,b,a	Primäre Farbe der Vorderseite
result.color.secondary	r,g,b,a	Sekundäre Farbe der Vorderseite
result.color.front	r,g,b,a	Primäre Farbe der Vorderseite
result.color.front.primary	r,g,b,a	Primäre Farbe der Vorderseite
result.color.front.secondary	r,g,b,a	Sekundäre Farbe der Vorderseite
result.color.back	r,g,b,a	Primäre Farbe der Rückseite
result.color.back.primary	r,g,b,a	Primäre Farbe der Rückseite
result.color.back.secondary	r,g,b,a	Sekundäre Farbe der Rückseite
result.fogcoord	f,*,*,*	Nebelkoordinate
result.pointsize	s,*,*,*	Punktgröße
result.texcoord	s,t,r,q	Texturkoordinate (Textureinheit 0)
result.texcoord[n]	s,t,r,q	Texturkoordinate (Textureinheit n)

Wie Eingangs bereits erwähnt, müssen wir alle Vertexattribute die wir nutzen wollen wieder zurückgeben, da OpenGL dies bei der Verwendung eines Vertexprogrammes nicht mehr für uns tut. Wollen wir also die in unserer Anwendung per glColor3f übergebene Vertexfarbe auch sehen, so müssen wir diese in unserem Vertexprogramm "durchschleifen", also einfach unverändert von unserem Eingangsregister ins passende Ausgangsregister schieben. Mit folgender Zeile im VP lässt sich das kurz und schmerzlos bewerkstelligen:

MOV result.color, vertex.color;

So ähnlich sieht die Sache dann auch aus, wenn wir Texturmapping (und damit Texturkoordinaten) verwenden wollen, diese müssen dann folgendermaßen durchgeschleift werden:

MOV result.texcoord, vertex.texcoord;

Wenn wir diese Zeile aus unserem VP weglassen würden, dann wäre die Übergabe der Texturenparameter in unserer Anwendung mittels glTexCoord2f sinnlos, da diese nicht verwendet würden.Anhand dieser zwei Beispiele sollte euch also recht schnell klar werden, das nur wieder ausgegebenen Vertexattribute auch sichtbar auf dem Schirm ankommen.

Matrixeigenschaften

Der Zugriff auf die Matrizen aus einem VP heraus ist natürlich ein essentielles Feature, dem mit den Matrixeigenschaften und deren Variationen zu genüge nachgekommen wird.Die unten aufgelisteten Matrizen besitzen nocheinmal jede Menge Parameter, die ihre Nutzung stark erweitern: .transpose liefert die umgestellte, .inverse die invertierte und .invtrans die aus obigen Eigenschaften kombinierte Matrix. Mittels der .row-Eigenschaft lässt sich dann letztendlich auf jede Reihe der Matrix zugreifen.

Eigenschaften	OpenGL-State
state.matrix.modelview[n](*)	Modelansichtsmatrix n
state.matrix.projection	Projektionsmatrix
state.matrix.mvp	Modelansichts-Projektionsmatrix
state.matrix.texture[n](*)	Texturmatrix n
state.matrix.palette[n]	Modelansichtspalettenmatrix n
state.matrix.program[n]	Programmatrix n

(*)= Der Index n kann hier auch weggelassen werden.Dann bezieht sich die Eigenschaft auf das Element 0.

Beispiele:

PARAM R1[4] = { state.matrix.modelview.invtrans };

Legt die umgekehte und umgestellte (inverse&transpose) Modelansichtsmatrix im Programmparameter R1 ab.

PARAM R2[4] = { state.matrix.projection };

Legt die Projektionsmatrix im Programmparameter R2 ab.

Materialeigenschaften

Auch in Sachen Materialeigenschaften kann auf alle erdenklichen Eigenschaften innerhalb eines VPs zugegriffen werden.

Eigenschaften	Komponenten
state.material.ambient	r,g,b,a
state.material.diffuse	r,g,b,a
state.material.specular	r,g,b,a
state.material.emission	r,g,b,a
state.material.shininess	s,0,0,1
state.material.front.ambient	r,g,b,a
state.material.front.diffuse	r,g,b,a
state.material.front.specular	r,g,b,a
state.material.front.emission	r,g,b,a
state.material.front.shininess	s,0,0,1
state.material.back.ambient	r,g,b,a
state.material.back.diffuse	r,g,b,a
state.material.back.specular	r,g,b,a
state.material.back.emission	r,g,b,a
state.material.back.shininess	s,0,0,1

Lichteigenschaften

Auch auf alle Lichteigenschaften kann innerhalb eines Vertexprogrammes direkt zugegriffen werden, so dass der Implementation eigener Beleuchtungsmodelle bzw. Effekte nichts mehr im Wege steht. Auch das bisherige Limit von 8 Hardwarepunktlichtern lässt sich mittels eines Vertexprogrammes leicht umgehen.

Eigenschaft	Komponenten	Bemerkung
state.light[n].ambient	r,g,b,a	Ambiente Farbe der Lichtquelle[n]
state.light[n].diffuse	r,g,b,a	Diffuse Farbe der Lichtquelle[n]
state.light[n].specular	r,g,b,a	Spekulative Farbe der Lichtquelle[n]
state.light[n].position	x,y,z,w	Position der Lichtquelle[n]
state.light[n].attenuation	a,b,c,e	Abschwächungsfaktorkonstanten und Spotlichtexponent der Lichtquelle[n]
state.light[n].spot.direction	x,y,z,c	Spotrichtung und Cosinus des Abfallwinkels der Lichquelle[n]
state.light[n].half	x,y,z,1	Unendlicher Halbwinkel der Lichtquelle [n]
state.lightmodel.ambient	r,g,b,a	Ambiente Farbe des Lichtmodells
state.lightmodel.scenecolor	r,g,b,a	Vordere Szenenfarbe des Lichtmodells
state.lightmodel.front.scenecolor	r,g,b,a	Vordere Szenenfarbe des Lichtmodells
state.lightmodel.back.scenecolor	r,g,b,a	Rückseitige Szenenfarbe des Lichtmodells
state.lightprod[n].ambient	r,g,b,a	Ambientes Farbprodukt des Frontmaterials der Lichtquelle[n]
state.lightprod[n].diffuse	r,g,b,a	Diffuses Farbprodukt des Frontmaterials der Lichtquelle[n]
state.lightprod[n].specular	r,g,b,a	Spekulatives Farbprodukt des Frontmaterials der Lichtquelle[n]
state.lightprod[n].front.ambient	r,g,b,a	Ambientes Farbprodukt des Frontmaterials der Lichtquelle[n]
state.lightprod[n].front.diffuse	r,g,b,a	Diffuses Farbprodukt des Frontmaterials der Lichtquelle[n]
state.lightprod[n].front.specular	r,g,b,a	Spekulatives Farbprodukt des Frontmaterials der Lichtquelle[n]
state.lightprod[n].back.ambient	r,g,b,a	Ambientes Farbprodukt des rückseitigen Materials der Lichtquelle[n]
state.lightprod[n].back.diffuse	r,g,b,a	Diffuses Farbprodukt des rückseitigen Materials der Lichtquelle[n]
state.lightprod[n].back.specular	r,g,b,a	Spekulatives Farbprodukt des rückseitigen Materials der Lichtquelle[n]

Texturkoordinatengenerierung

Die folgenden Variablen erlauben den Zugriff auf die Parameter von OpenGLs Mechanismen zur Generierung von Texturkoordinaten.

Eigenschaft	Komponenten
state.texgen[n].eye.s	a,b,c,d
state.texgen[n].eye.t	a,b,c,d
state.texgen[n].eye.r	a,b,c,d
state.texgen[n].eye.q	a,b,c,d
state.texgen[n].object.s	a,b,c,d
state.texgen[n].object.t	a,b,c,d
state.texgen[n].object.r	a,b,c,d
state.texgen[n].object.q	a,b,c,d

Nebeleigenschaften

Eigenschaft	Komponenten	Bemerkung
state.fog.color	r,g,b,a	Nebelfarbe
state.fog.params	d,s,e,r	Nebeldichte,Nebelstart,Nebelende und Nebelreichweite (=1/(Ende-Start)

Punkteigenschaften

Eigenschaft	Komponenten	Bemerkung
state.point.size	s,n,x,f	Punktgröße, Untergrenze, Obergrenze, Fadegrenze
state.point.attenuation	a,b,c,1	Punktgrößenabschwächung

Schnittflächen

Eigenschaft	Komponenten	Bemerkung
state.clip[n].plane	a,b,c,d	Koeffizienten der Schnittfläche n

So... das waren erstmal alle für Vertexprogramme der Version 1.0 vordefinierten Statebindings und Attributregister die zur Verfügung stehen.Wer hier einige Parameter vermissen sollte (wovon ich allerdings nicht ausgehe), der dürfte im nächsten Kapitel eine Lösung für sein Problem finden.

Parameterübergabe

Natürlich wären Vertexprogramme in ihrer Funktionalität recht eingeschränkt, wenn sie keine Möglichkeit bieten würden um Parameter (abgesehen von den Attributregistern und Statebindings) von der Anwendung an das VP zu übergeben. Dessen waren sich die Macher auch bewusst, und haben deshalb gleich drei Möglichkeiten zur Parameterübergabe an das Vertexprogramm vorgesehen, welche wir uns in diesem Kapitel mal genauer ansehen werden.

Vertexattribute

Hiermit hat man die Möglichkeit Nx4 Parameter auf per-Vertex-Basis an das VP zu übergeben, auf die man mittels des Vertexattributregisters vertex.attrib[n] innerhalb des VPs zugreifen kann. Zur Übergabe dieser Vertexattribute gibt es die Prozeduren glVertexAttrib4*ARB(index, x,y,z,w) und glVertexAttrib4*vARB(index, @xyzw), die entweder direkt vier Werte oder einen Zeiger darauf in das über index angegebene Vertexattribut schreiben. Bei der Nutzung von VertexArrays fällt diese per-Vertex-Lösung natürlich flach. Hier bietet die Funktion glVertexAttribPointerARB einen Ausweg, mit deren Hilfe man die Vertexattribute passend zum Vertexarray in einem Pointer übergeben kann.

Programmbeispiel (Übergabe der Vertexfarbe im Vertexattribut 1):

Anwendung:

glVertexAttrib4fARB(0 ,0.5,1,0.5,0)

Vertexprogramm:

MOV result.color, vertex.attrib[1];

Anmerkung: Auch wenn ich im obigen Beispiel die Vertexfarbe über ein Vertexattribut übergebe, so sollte man darauf in der Praxis verzichten.Wenn es nämlich einen OpenGL-Befehl gibt um ein Vertexattribut zu übergeben (glTexCoord, glColor), dann sollte man diesen auch verweden.Vertexattribute sind eher zur Übergabe von Werten für eigenen Berechnungen gedacht.

Lokale Programmparameter

Je nach OpenGL-Implementation lassen sich für jedes verwendete Vertexprogramm mindestens 96 lokale Programmparameter, bestehend aus vier Fließkommakomponenten (x, y, z, w) übergeben, die natürlich nur von diesem VP genutzt werden können. Wenn möglich sollte man diese Art der Parameterübergabe wählen, da die Anzahl der globalen Parameter (siehe nächster Abschnitt) je nach Implementation recht schnell knapp werden kann. Übergeben werden die lokalen Programmparameter an das momentan gebundenen Vertexprogramm mittels der Prozeduren glProgramLocalParameter4*ARB(target, index, x,y,z,w) und glProgramLocalParameter4*vARB(target, index, @xyzw). Der Zugriff auf die lokalen Parameter innerhalb des Vertexprogrammes erfolg über das Register program.local[n], wobei n in innerhalb von [0..GL_MAX_PROGRAM_LOCAL_PARAMETERS_ARB-1] liegt.Man sollte deshalb immer im Hinterkopf behalten, das die maximale Anzahl lokaler (wie auch globaler) Parameter je nach verwendeter Hardware unterschiedlich sein kann.(bei einer GeForce2 z.B. max 96, Radeon9700 maximal 256).

Programmbeispiel:

Anwendung:

glProgramLocalParameter4fARB(GL_VERTEX_PROGRAM_ARB, 0, 1,1,0,0)

Vertexprogramm:

MOV result.fogcoord, program.local[0];

Globale Programmparameter (aka Umgebungsparameter)

Auch von diesem Parametertyp muss die OpenGL-Implementation mindestens 96 Stück bieten, auf die JEDES Vertexprogramm zugreifen kann. Die Übergabe dieser Parameter funktioniert haargenau so wie dies bei den lokalen Parametern der Fall war über die Prozeduren glProgramEnvParameter4*ARB(target, index, x,y,z,w) und glProgramEnvParameter4*vARB(target, index, @xyzw). Der Zugriff wird über das Register program.env[n] bewerkstelligt, wobei n innnerhalb von [0..GL_MAX_PROGRAM_ENV_PARAMETERS_ARB-1] liegt. Auch hier ist die Anzahl der maximalen Parameter von der verwendeten Hardware abhängig.

Programmbeispiel:

Anwendung:

glProgramEnvParameter4fARB(GL_VERTEX_PROGRAM_ARB, 0 ,1,1,0,0)

Vertexprogramm:

MOV result.texcoord, program.env[0];

Variablen

Wie in jeder Programmiersprache der Fall (und auch grundlegender Bestandteil einer solchen), so gibt es auch innerhalb eines Vertexprogrammes verschiedene Variablentypen. Die genutzten Variablen können überall im Programm deklariert werden. Dies muss allerdings vor deren erster Nutzung geschehen (klingt logisch, oder?). Folgendes ist allerdings bei der Vergabe von Variablennamen zu beachten:

• Gültige Zeichen sind Buchstaben (A bis Z, a bis Z), Ziffern (0 bis 9), Unterstriche und Dollarzeichen
• Das erste Zeichen darf KEINE Ziffer sein
• Name darf kein vorbelegter Bezeichner sein (z. B. vertex, TEMP, ADDRESS)
• Groß- und Kleinschreibung müssen beachtet werden

Adressregister

Vorzeichenbehaftete Vierkomponentenvektoren im Integerformat, bei denen jedoch nur die X-Komponente adressierbar ist.Die maximal deklarierbare Anzahl von Adressregistern ist in GL_MAX_PROGRAM_ADDRESS_REGISTERS_ARB abgelegt. Deklarationsbeispiele:

ADDRESS R1;
ADDRESS RegA, RegB, RegC;

Temporäre Variablen

Vierkomponentenvektoren im Fliesskommaformat, die wie der Name schon vermuten lässt hauptsächlich zur Zwischenspeicherung von Berechnungsergebnissen genutzt werden. Die Anzahl der maximal deklarierbaren temporären Variablen lässt sich über das Token GL_MAX_PROGRAM_TEMPORARIES_ARB ermitteln. Deklarationsbeispiele:

TEMP Temp1;
TEMP Erg1, Erg2, Speicher1;

Programmparameter

Programmparameter sind im Grunde genommen nichts anderes als Konstanten, und werden deshalb auch genauso deklariert.Die Anzahl der maximal deklarierbaren Konstanten ist in GL_MAX_PROGRAM_PARAMETERS_ARB hinterlegt.Natürlich kann man neben eindimensionalen auch mehrdimensionale Arrays (siehe Deklarationsbeispiel Nr. 2) deklarieren.Die Angabe der Arraygröße in eckigen Klammern hinter dem Variablennamen ist optional. Deklarationsbeispiele:

PARAM R1 = {1.0, 3.5, 2.0, 8.0, 1.5};
PARAM R2 = { {1.0, 3.0, 1.0}, {1.0, 2.0, 2.0} };

Ausgabevariablen

Mittels der Ausgabevariablen kann man beliebige Ausgabevariablen (siehe Vertex-Ergebnis-Register) an eine binden und so eine Referenz auf dieses Ergebnisregister erstellen. Deklarationsbeispiele:

OUTPUT OutColor = result.color;
OUTPUT OutFogCoord = result.fogcoord;

Abfrage der Implementationsgrenzen

Besonders bei aufwendigeren Vertexprogammen ist es oft nötig zu wissen, wie viele Variablen man zur Verfügung hat, um evtl. auf mehrere Durchläufe oder weniger komplexe Vertexprogramme auszuweichen. Die GL_VERTEX_PROGRAM_ARB-Erweiterung bietet hierzu jede Menge Abfrageparameter auf die man denn ggf. reagieren kann. Mittels der Prozedur glGetProgramivARB(target : TGLenum;pname : TGLenum;params: PGLint) lassen sich diese implementationsabhängigen Grenzen schnell ermitteln.Das Target muss in unserem Falle natürlich gleich GL_VERTEX_PROGRAM_ARB sein. Welche maximale Variablenanzahl sich mit welchem Token ermitteln lässt, kann man dem entsprechenden Kapiteln zu den verschiedenen Variablentypen entnehmen.

Der Befehlssatz

Der GL_VERTEX_PROGRAM_ARB-Befehlssatz besteht aus 27 leistungsfähigen SIMD-Instruktionen (Single Instruction/Multiple Data), die speziell für die Grafikprogrammierung entwickelt wurden und auf Vertexbasis arbeiten.

ABS (Absolute)

Syntax: ABS dest, v

Ziel: Vektor Quelle(n) : Vektor

Kopiert den absoluten Wert von v in das Register dest.

Funktion:

tmp = VectorLoad(op0);
result.x = fabs(tmp.x);
result.y = fabs(tmp.y);
result.z = fabs(tmp.z);
result.w = fabs(tmp.w);

ADD (Add)

Syntax: ADD dest, v0, v1

Ziel: Vektor Quelle(n) : Vektor,Vektor

Addiert das Register v mit dem Register v und kopiert das Ergebnis in das Register dest.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
result.x = tmp0.x + tmp1.x;
result.y = tmp0.y + tmp1.y;
result.z = tmp0.z + tmp1.z;
result.w = tmp0.w + tmp1.w;

ARL (Address register load)

Syntax: ARL AddrReg, Src.C

Ziel: Adressregisterkomponente Quelle(n) : Vektor

Lädt das Register Src.C (wobei C entweder x,y,z oder w) in das Adressregister AddrReg und rundet zum nächstkleineren Integerwert ab (FLR).

Funktion:

result = floor(ScalarLoad(op0));

DP3 (3-component dot product)

Syntax: DP3 dest, v0, v1

Ziel: Skalar reproduziert über 4-Komponentenvektor Quelle(n) : Vektor,Vektor

Berechnet das 3-Komponenten Punktprodukt aus v0 und v1 und legt das Skalar in dest ab.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
dot = (tmp0.x * tmp1.x) + (tmp0.y * tmp1.y) + (tmp0.z * tmp1.z);
result.x = dot;
result.y = dot;
result.z = dot;
result.w = dot;

DP4 (4-component dot product)

Syntax: DP4 dest, v0, v1

Ziel: Skalar reproduziert über 4-Komponentenvektor Quelle(n) : Vektor,Vektor

Berechnet das 4-Komponenten Punktprodukt aus v0 und v1 und legt das Skalar in dest ab.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
dot = (tmp0.x * tmp1.x) + (tmp0.y * tmp1.y) + (tmp0.z * tmp1.z) + (tmp0.w * tmp1.w);
result.x = dot;
result.y = dot;
result.z = dot;
result.w = dot;

DPH (homogeneous dot product)

Syntax: DP3 dest, v0, v1

Ziel: Skalar reproduziert über 4-Komponentenvektor Quelle(n) : Vektor,Vektor

Berechnet das homogene Punktprodukt aus v0 und v1 und legt das Skalar in dest ab.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1):
dot = (tmp0.x * tmp1.x) + (tmp0.y * tmp1.y) + (tmp0.z * tmp1.z) + tmp1.w;
result.x = dot;
result.y = dot;
result.z = dot;
result.w = dot;

DST (distance vector)

Syntax: DST dest, v0, v1

Ziel: Vektor Quelle(n) : Vektor,Vektor

Berechnet den Distanzvektor zwischen v0 und v1 und legt diesen in dest ab.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
result.x = 1.0;
result.y = tmp0.y * tmp1.y;
result.z = tmp0.z;
result.w = tmp1.w;

EX2 (exponential base 2)

Syntax: EX2 dest, s

Ziel: Skalar reproduziert über 4-Komponentenvektor Quelle(n) : Skalar

Berechnet die Potenz von s zur Basis 2 aus und legt das Ergebnis als Skalar in dest ab.

Funktion:

tmp = ScalarLoad(op0);
result.x = Approx2ToX(tmp);
result.y = Approx2ToX(tmp);
result.z = Approx2ToX(tmp);
result.w = Approx2ToX(tmp);

EXP (exponential base 2 (approximate))

Syntax: EXP dest, s

Ziel: Vektor Quelle(n) : Skalar

Berechnet die Potenz von s zur Basis 2 aus und legt das Ergebnis (Annäherungswert) als Vektor in dest ab.

Funktion:

tmp = ScalarLoad(op0);
result.x = 2^floor(tmp);
result.y = tmp - floor(tmp);
result.z = RoughApprox2ToX(tmp);
result.w = 1.0;

FLR (floor)

Syntax: FLR dest, v

Ziel: Vektor Quelle(n) : Vektor

Rundet den im Register v abgelegten Wert zum nächstkleineren Integerwert ab und legt das Ergebnis im Register dest ab.

Funktion:

tmp = VectorLoad(op0);
result.x = floor(tmp.x);
result.y = floor(tmp.y);
result.z = floor(tmp.z);
result.w = floor(tmp.w);

FRC (fraction)

Syntax: FRC Dest, v

Ziel: Vektor Quelle(n) : Vektor

Kopiert die Nachkommateile des in v übergebenen Vektors an das Register Dest.

Funktion:

tmp = VectorLoad(op0);
result.x = fraction(tmp.x);
result.y = fraction(tmp.y);
result.z = fraction(tmp.z);
result.w = fraction(tmp.w);

LG2 (logarithm base 2)

Syntax: LG2 dest, s

Ziel: Skalar reproduziert über 4-Komponentenvektor Quelle(n) : Skalar

Berechnet den Logarithmus von s zur Basis 2 und legt diesen als Skalar reproduziert über einen Vektor in dest ab.

Funktion:

tmp = ScalarLoad(op0);
result.x = ApproxLog2(tmp);
result.y = ApproxLog2(tmp);
result.z = ApproxLog2(tmp);
result.w = ApproxLog2(tmp);

LIT (compute light coefficients)

Syntax: LIT dest, v

Ziel: Vektor Quelle(n) : Vektor

Berechnet die Beleuchtungskoeffizienten von v und legt diese in dest ab.

Funktion:

tmp = VectorLoad(op0);
if (tmp.x < 0) tmp.x = 0;
if (tmp.< 0) tmp.y = 0;
if (tmp.w < -(128.0-epsilon)) tmp.w = -(128.0-epsilon);
else if (tmp.w >128-epsilon) tmp.w = 128-epsilon;
result.x = 1.0;
result.y = tmp.x;
result.z = (tmp.x > 0) ? RoughApproxPower(tmp.y, tmp.w) : 0.0;
result.w = 1.0;

LOG (logarithm base 2 (approximate))

Syntax: LOG dest, s

Ziel: Vektor Quelle(n) : Skalar

Berechnet den Logarithmus von s zur Basis 2 und legt diesen als Annäherungswert in dest ab.

Funktion:

tmp = fabs(ScalarLoad(op0));
result.x = floor(log2(tmp));
result.y = tmp / 2^(floor(log2(tmp)));
result.z = RoughApproxLog2(tmp);
result.w = 1.0;

MAD (multiply and add)

Syntax: MAD dest, v0, v1, v2

Ziel: Vektor Quelle(n) : Vektor,Vektor,Vektor

Der Wert von v2 wird zum Produkt von v0 und v1 addiert und im Register dest abgelegt.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
tmp2 = VectorLoad(op2);
result.x = tmp0.x * tmp1.x + tmp2.x;
result.y = tmp0.y * tmp1.y + tmp2.y;
result.z = tmp0.z * tmp1.z + tmp2.z;
result.w = tmp0.w * tmp1.w + tmp2.w;

MAX (maximum)

Syntax: MAX dest, v0, v1

Ziel: Vektor Quelle(n) : Vektor,Vektor

Ermittelt die Maximalwerte der Vektoren v0 und v1 per Komponente, und legt diese in dest ab.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
result.x = (tmp0.x > tmp1.x) ? tmp0.x : tmp1.x;
result.y = (tmp0.y > tmp1.y) ? tmp0.y : tmp1.y;
result.z = (tmp0.z > tmp1.z) ? tmp0.z : tmp1.z;
result.w = (tmp0.w > tmp1.w) ? tmp0.w : tmp1.w;

MIN (minimum)

Syntax: MIN dest, v0, v1

Ziel: Vektor Quelle(n) : Vektor,Vektor

Ermittelt die Minimalwerte der Vektoren v0 und v1 per Komponente, und legt diese in dest ab.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
result.x = (tmp0.x > tmp1.x) ? tmp1.x : tmp0.x;
result.y = (tmp0.y > tmp1.y) ? tmp1.y : tmp0.y;
result.z = (tmp0.z > tmp1.z) ? tmp1.z : tmp0.z;
result.w = (tmp0.w > tmp1.w) ? tmp1.w : tmp0.w;

MOV (move)

Syntax: MOV dest, src

Ziel: Vektor Quelle(n) : Vektor

Kopiert den Inhalt des Quellregisters src in das Zielregister dest.

Funktion:

result = VectorLoad(op0);

MUL (multiply)

Syntax: MUL dest, v0, v1

Ziel: Vektor Quelle(n) : Vektor,Vektor

Multipliziert die Komponenten von v0 und v1,und schreibt das Ergebnis in das Zielregister dest.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
result.x = tmp0.x * tmp1.x;
result.y = tmp0.y * tmp1.y;
result.z = tmp0.z * tmp1.z;
result.w = tmp0.w * tmp1.w;

POW (exponentiate)

Syntax: POW dest, s0, s1

Ziel: Skalar reproduziert über 4-Komponentenvektor Quelle(n) : Skalar,Skalar

Errechnet die Potenz von s1 zur Basis s0 und legt das Ergebnis als über den Zielvektor dest reproduzierten Skalar ab.

Funktion:

tmp0 = ScalarLoad(op0);
tmp1 = ScalarLoad(op1);
result.x = ApproxPower(tmp0, tmp1);
result.y = ApproxPower(tmp0, tmp1);
result.z = ApproxPower(tmp0, tmp1);
result.w = ApproxPower(tmp0, tmp1);

RCP (reciprocal)

Syntax: RCP dest, s

Ziel: Skalar reproduziert über 4-Komponentenvektor Quelle(n) : Skalar

Invertiert den in s abgelegten Wert und reproduziert ihn über das Zielregister dest.

Funktion:

tmp = ScalarLoad(op0);
result.x = ApproxReciprocal(tmp);
result.y = ApproxReciprocal(tmp);
result.z = ApproxReciprocal(tmp);
result.w = ApproxReciprocal(tmp);

RSQ (reciprocal square root)

Syntax: RSQ dest, s

Ziel: Skalar reproduziert über 4-Komponentenvektor Quelle(n) : Skalar

Berechnet die umgekehrte Wurzel des absoluten Wertes in s und reproduziert das Ergebnis über das Zielregister dest.

Funktion:

tmp = fabs(ScalarLoad(op0));
result.x = ApproxRSQRT(tmp);
result.y = ApproxRSQRT(tmp);
result.z = ApproxRSQRT(tmp);
result.w = ApproxRSQRT(tmp);

SGE (set on greater than or equal)

Syntax: SGE dest, v0, v1

Ziel: Vektor Quelle(n) : Vektor,Vektor

Führt ein bedingtes Setzen von 1.0 oder 0.0 der einzelnen Komponenten durch.1.0 wird der Komponente in dest zugewiesen, falls die Komponente in v0 größer oder gleich der Komponente in v1 ist.Ansonsten wird der Komponente in dest der Wert 0.0 zugewiesen.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
result.x = (tmp0.x >= tmp1.x) ? 1.0 : 0.0;
result.y = (tmp0.y >= tmp1.y) ? 1.0 : 0.0;
result.z = (tmp0.z >= tmp1.z) ? 1.0 : 0.0;
result.w = (tmp0.w >= tmp1.w) ? 1.0 : 0.0;

SLT (set on less than)

Syntax: SLT dest, v0, v1

Ziel: Vektor Quelle(n) : Vektor,Vektor

Führt ein bedingtes Setzen von 1.0 oder 0.0 der einzelnen Komponenten durch.1.0 wird der Komponente in dest zugewiesen, falls die Komponente in v0 kleiner als die Komponente in v1 ist.Ansonsten wird der Komponente in dest der Wert 0.0 zugewiesen.

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
result.x = (tmp0.x < tmp1.x) ? 1.0 : 0.0;
result.y = (tmp0.y < tmp1.y) ? 1.0 : 0.0;
result.z = (tmp0.z < tmp1.z) ? 1.0 : 0.0;
result.w = (tmp0.w < tmp1.w) ? 1.0 : 0.0;

SUB (subtract)

Syntax: SUB dest, v0, v1

Ziel: Vektor Quelle(n) : Vektor,Vektor

Subtrahiert den in v1 hinterlegten Vektor von v0 und legt das Ergebnis in dest ab. Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
result.x = tmp0.x - tmp1.x;
result.y = tmp0.y - tmp1.y;
result.z = tmp0.z - tmp1.z;
result.w = tmp0.w - tmp1.w;

SWZ (extended swizzle)

Syntax: SWZ dest, v

Ziel: Vektor Quelle(n) : Vektor

Erweiterte Tauschfunktion für die einzelnen Vektorbestandteile von v, die dann in den Zielvektor dest geschrieben werden.

Funktion :

tmp = VectorLoad(op0);
result.x = ExtSwizComponent(tmp, xSelect, xNegate);
result.y = ExtSwizComponent(tmp, ySelect, yNegate);
result.z = ExtSwizComponent(tmp, zSelect, zNegate);
result.w = ExtSwizComponent(tmp, wSelect, wNegate);

XPD (cross product)

Syntax: XPD dest, v0, v1

Ziel: Vektor Quelle(n) : Vektor,Vektor

Berechnet das Kreuzprodukt von v0 und v1, und legt dieses im Zielvektor dest ab (nur XYZ-Komponente, W ist danach undefiniert).

Funktion:

tmp0 = VectorLoad(op0);
tmp1 = VectorLoad(op1);
result.x = tmp0.y * tmp1.z - tmp0.z * tmp1.y;
result.y = tmp0.z * tmp1.x - tmp0.x * tmp1.z;
result.z = tmp0.x * tmp1.y - tmp0.y * tmp1.x;

Geschafft! Das ist der komplette Befehlssatz wie er uns momentan zur Verfügung steht.Er bietet ggü. der NV_VERTEX_PROGRAM-Erweiterung, aus der GL_VERTEX_PROGRAM_ARB letztendlich hervorgegangen ist, 10 neue Befehle und sollte so ziemlich alle Bedürfnisse befriedigen können. Wenn nicht, dann lassen sich die meisten vermissten Befehle schnell aus einer Kombination mehrerer bereits vorhandener Befehle herleiten. Ich habe mir beim Übertragen der Funktionsbeschreibung ins Deutsche so viel Mühe wie möglich gegeben, aber da es bei einigen Befehlen einfach nicht ausreicht diese in einem Satz kurz zu beschreiben, gibts noch zu jedem Befehl den Pseudocode der seine Funktion genau beschreibt. Diesen Pseudocode habe ich der GL_VERTEX_PROGRAM_ARB-Spezifikation entnommen, der euch deshalb die Funktionsweise der einzelnen Befehle und den Inhalt des Ergebnisregisters vor Augen führen sollte.

Ein etwas komplexeres Vertexprogramm

Nachdem die letzten Kapitel aufgrund der Materie leider etwas trocken waren, werfen wir uns jetzt wieder voll in die Praxis und schauen uns ein etwas komplexeres Vertexprogramm im Detail an um das was wir in den letzten Kapiteln gelernt haben etwas zu vertiefen.

Folgendes VP berechnet simple Umgebungs-, spekulative und diffuse Beleuchtung einer einzelnen (ungerichteten) Lichtquelle mit einem lokalen Betrachter. Die Lichtparameter werden vom OpenGL-State der Lichtquelle[0] übernommen und können so innerhalb unserer Anwendung kontrolliert werden:

!!ARBvp1.0
# Eingangsattribute
ATTRIB iPos = vertex.position;
ATTRIB iNormal = vertex.normal;
#Programmparameter
PARAM mvinv[4] = { state.matrix.modelview.invtrans };
PARAM mvp[4] = { state.matrix.mvp };
PARAM lightDir = state.light[0].position;
PARAM halfDir = state.light[0].half;
PARAM specExp = state.material.shininess;
PARAM ambientCol = state.lightprod[0].ambient;
PARAM diffuseCol = state.lightprod[0].diffuse;
PARAM specularCol = state.lightprod[0].specular;
# Temporäre Variablen 
TEMP eyeNormal, temp, dots, lightcoefs;
# Ausgangsattribute
OUTPUT oPos = result.position;
OUTPUT oColor = result.color;
# Vertex in Clipkoordinaten umwandeln
DP4 oPos.x, mvp[0], iPos;
DP4 oPos.y, mvp[1], iPos;
DP4 oPos.z, mvp[2], iPos;
DP4 oPos.w, mvp[3], iPos;
# Normale in eyespace transformieren
DP3 eyeNormal.x, mvinv[0], iNormal;
DP3 eyeNormal.y, mvinv[1], iNormal;
DP3 eyeNormal.z, mvinv[2], iNormal;
# Diffuses und spekulatives Punktprodukt berechnen
# und unter Nutzung von LIT die
# Beleuchtungskoeffizienten berechnen
DP3 dots.x, eyeNormal, lightDir;
DP3 dots.y, eyeNormal, halfDir;
MOV dots.w, specExp.x;
LIT lightcoefs, dots;
# Farbbestandteile sammeln und addieren
MAD temp, lightcoefs.y, diffuseCol, ambientCol;
MAD oColor.xyz, lightcoefs.z, specularCol, temp;
MOV oColor.w, diffuseCol.w;
MUL oColor.xyz, vertex.color, temp;
END

Das sieht dann schonmal etwas komplexer aus als unser erstes Beispiel, spiegelt jedoch immernoch ein recht einfaches Vertexprogramm aus.Komplexere Anwendungen nutzen meist mehrere Vertexprogramme in Verbindung mit Pixelshadern (Fragmentprogrammen) um komplexe Berechnungen und Effekte zu realisieren. Sehen wir uns nun aber unser VP mal etwas genauer an:

ATTRIB iPos = vertex.position;
ATTRIB iNormal = vertex.normal;

Hier deklarieren wir erstmal die Vertexeingangsattribute die wir in unserem Programm brauchen. Man beachte das eine solche Deklaration nicht unbedingt notwendig ist, und man auf die Vertexattribute auch direkt im VP zugreifen kann.Allerdings ists für die Übersichtlichkeit oftmals besser (besonders bei der häufigen Nutzung der Attribute) diese mit eigenen Variablennamen zu versehen.

PARAM mvinv[4] = { state.matrix.modelview.invtrans };
PARAM mvp[4] = { state.matrix.mvp };

Hier deklarieren wir zwei Programmparameter die jeweils Referenzen auf zwei OpenGL-States darstellen. mvinv ist eine Referenz auf die aktuelle umgekehrte umgestellte Modelansichtsmatrix, während mvp eine Referenz auf die aktuelle Modelansichts- und Projektionsmatrix darstellt.

PARAM lightDir = state.light[0].position;
PARAM halfDir = state.light[0].half;

Diese beiden Programmparameter referenzieren zwei wichtige Lichtparameter die unser VP benötigt. lightDir ist eine Referenz der Position von Lichtquelle[0], und halfDir referenziert den unendlichen Halbwinkel dieser Lichtquelle.

PARAM specExp = state.material.shininess;

Der Programmparameter specExp referenziert die Reflektivität des aktuellen Materials.

PARAM ambientCol = state.lightprod[0].ambient;
PARAM diffuseCol = state.lightprod[0].diffuse;
PARAM specularCol = state.lightprod[0].specular;

Diese drei Programmparameter referenzieren die verschiedenen Lichtprodukte der Lichtquelle[0], die wir zur Beleuchtungsberechnung benötigen.

TEMP eyeNormal, temp, dots, lightcoefs;

Hier werden einige temporäre Vektoren definiert, die wir innerhalb des VPs zur Zwischnespeicherung unserer Berechnungen benötigten.

OUTPUT oPos = result.position;
OUTPUT oColor = result.color;

Hier referenzieren wir unter kürzeren Variablenamen die Vertexattribute die unser VP weitergeben soll. Auch hier gilt, das man innerhalb des VPs genausogut direkt die Ausgaberegister benutzen könnte.

DP4 oPos.x, mvp[0], iPos;
DP4 oPos.y, mvp[1], iPos;
DP4 oPos.z, mvp[2], iPos;
DP4 oPos.w, mvp[3], iPos;

Wie in unserem ersten Vertexprogramm wandeln wir hier die Vertexposition durch das 4-Komponenten Punktprodukt mit der Modelansichtsmatrix in Clipkoordinaten um damit diese korrekt auf den Bildschirm gebracht werden.

DP3 eyeNormal.x, mvinv[0], iNormal;
DP3 eyeNormal.y, mvinv[1], iNormal;
DP3 eyeNormal.z, mvinv[2], iNormal;

Hier wandeln wir die Vertexnormale mittels eines 3-Komponenten Punktproduktes in Betrachtungskoordinaten um und legen diese im temporären Vektor eyeNormal ab.

DP3 dots.x, eyeNormal, lightDir;
DP3 dots.y, eyeNormal, halfDir;
MOV dots.w, specExp.x;
LIT lightcoefs, dots;

In diesen Zeilen werden sowohl das diffuse als auch das spekulative Punktprodukt berechnet und mittels der Funktion LIT werden dann die Beleuchtungskoeffizienten berechnet und im Register lightcoefs abgelegt.

MAD temp, lightcoefs.y, diffuseCol, ambientCol;
MAD oColor.xyz, lightcoefs.z, specularCol, temp;
MOV oColor.w, diffuseCol.w;
MUL oColor.xyz, vertex.color, temp;

Nun werden noch die verschiedenen Farb- und Lichtbestandteile addiert und multipliziert und im Ausgaberegsiter oColor (welches vertex.color referenziert) nach Aussen weitergegeben.Hiermit ist die Lichtberechnung abgeschlossen.

So, das war nun ein etwas komplexeres Vertexprogramm mit einer hoffentlich mehr als ausreichenden detaillierten Beschreibung. Ich hoffe das euch dies (und natürlich auch der Rest des Tutorials) beim Verständis der Programmierung von Vertexprogrammen stark geholfen hat. Nun sollte euch eigentlich nichts mehr beim Erstellen eigener Vertexprogramme und damit verbunden besonderer Effekte im Wege stehen.

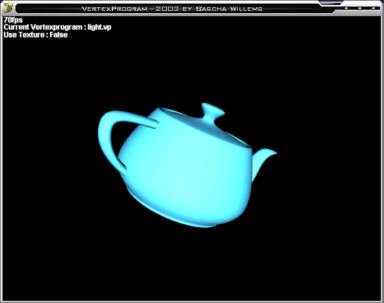
Abschliessend noch ein Bild von unserem neuen Vertexprogramm in Aktion. Gut zu sehen (auf einem statischen Bild leider weniger als in Aktion) ist die Wirkung der Beleuchtungsberechnungen auf unseren berühmten Teetopf:

Beispiele

Um euch bei euren Bemühungen noch etwas anzuspornen, und um euch mal nen kleinen Eindruck von dem zu geben, was man mit Vertexprogrammen (und teilweise im Zusammenspiel mit Fragmentprogrammen) so alles machen kann, gibts hier ne kleine Gallerie in denen selbige zum Erzielen toller Effekte genutzt wurden:

Keyframe Animation	Physikalisch korrekte und natürliche Animationen	Vorbereitung zum Bumpmapping
Celshading (Toonshading)	Eigene Beleuchtungsmethoden	Reflektionen und Refraktion

Die Zukunft

Vertexprogramme sind inzwischen aufgrund ihrer (hardwaretechnischen) weiten Verbreitung nicht mehr wegzudenken, und werden in Zukunft selbst bei zunehmender Unterstützung von Pixelshadern nicht mehr aus der Grafikwelt wegzudenken sein, weshalb ein wenig Fachwissen auf diesem Gebiet natürlich nicht schaden kann.

Was sich allerdings in der Zukunft stark ändern wird, ist die Art in der diese Vertexprogramme geschrieben werden.Weg von der recht einschränkenden Assemblersprache (ohne Sprünge und Verzweigungen) hin zu einer Shaderhochsprache die das Programmieren von VPs in einer C-ähnlichen Syntax (jaja, Objectpascal wäre mir auch lieber gewesen...) ermöglichen wird.

Dies Spezeifkationen für diese neue Shadersprache namens glSlang sind bereits fest und werden mit OpenGL2.0 auf dem Markt landen. Wer sich jetzt schonmal über diese neue Shaderhochsprache (HLSL) informieren will, der sollte sich unbedingt folgende Dokumente zu Gemüte führen:

• OpenGL Shading Language Draft v 1.05 (PDF)
• The OpenGL Shading Language (PDF)
• Introduction to the OpenGL Shading Language (PDF)
• OpenGL 2.0 Update - March 21st 2002 (PDF)

Quellen

Leider siehts in Sachen Dokumentation bei dieser relativ neuen OpenGL-Extension noch recht dürftig aus, weshalb ich euch nur auf folgende zwei "Dokumente" verweisen kann, die mir auch teilweise als Basis für dieses Tutorial dienten:

• ARB_Fragment_Program - Präsentation GDC2003
• GL_VERTEX_PROGRAM_ARB - Offizielle Spezifikation

Schlusswort

So, das wars!

Und ich hoffe euch hat das Ganze hier genausoviel Spaß gemacht wie mir, denn ich habe mir während des Schreibens dieses Tutorials die Nutzung von Vertexprogrammen beigebracht und hoffe das ihr die Technik nach dem Lesen dieses Tuts nun auch gerafft habt, und diese auch schön fleissig in euren Programmen nutzt. Denn Vertexprogramme (und später auch Pixelshader) sind leistungsstarke Features der neuen Grafikkartengeneration, die man nicht ungenutzt lassen sollte!

Wenn ihr euch mal einige Vertexprogramme (Shader) in Aktion sehen wollt, dann müsst ihr euch unbedingt mal in der Entwicklersektion von nVidia umsehen, denn dort gibts massig Anwendungsbeispiele zu diesem Thema!

Euer

Son of Satan(webmaster_at_delphigl.de)

Dateien

• Beispiel-Quelltext (Delphi)
• Beispiel-Programm

Vorhergehendes Tutorial: Tutorial_Vertexbufferobject	Zur Übersicht	Nächstes Tutorial: Tutorial_NVOcclusionQuery
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen.