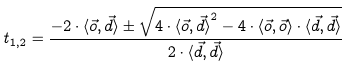Tutorial Raytracing - Grundlagen I
Bitte haben Sie etwas Geduld und nehmen Sie keine Änderungen vor, bis der Artikel hochgeladen wurde. |
Inhaltsverzeichnis
Tutorial Raytracing - Grundlagen I
Einführung
Soso. Da melde ich mich mal wieder zurück mit einem kleinen Tutorial bezüglich Raytracing. Ihr sollt ja auch gelegentlich was neues lernen. Es ist zwar etwas schade, daß nur noch selten Tutorias aus der Community kommen - ich hoffe ja immernoch, daß sich das irgendwann wieder ändern wird. Nunja. Was hat es also mit dem Raytracing auf sich? Und warum heisst dieses Tutorial Grundlagen I? Ich will es euch erklären. Beim Raytracing verfolgt man im Gegensatz zum Rastern wie es etwa OpenGl oder Direct3D machen, einen anderen Ansatz. Statt Objekte in Polygone zu zerschneiden und sie dann auf den Bildschirm per Z-Buffer zu projezieren, wirf die Kamera Strahlen in die Szenerie und auf jedem Strahl prüft man, ob sich ein Objekt mit dem Strahl schneidet. Man verliert dadurch sehr deutlich geschwindigkeit: die wenigsten Raytracer sind so schnell, daß man Interaktiv damit arbeiten kann. Wozu also ist dann Raytracing gut? Man kann im Raytracer hoch realistisch wirkende Bilder erzeugen und auch Verfahren verwenden, die im Rasterizer nich oder kaum nachzubauen sind - die gute alte Grafikkarte muss dabei aber nicht völlig unnütz werden: Diese besitzen sehr flotte und massiv parallele Geometrie-Einheiten, die auch im Raytracer Verwendung finden können - dies ist aber viel zu speziell für unser kleines Tutorial. Was sich im Bereich interaktiver Grafik allerdings anbietet, ist Raytracer ein wenig umzumodeln und mit ihnen statische Lightmaps erzeugen oder sie zur Selection missbrauchen. Das einzige Problem welches wir dabei haben: Wir müssen alles von Grund auf zusammenbasteln - nicht so schön, wie bei OpenGl wo man nach ein paar Stunden schöne Bilder zeichnen kann. Wir werden da wohl etwas länger brauchen, aber ewig wird es auch nicht dauern ;-)
Die Griechische Vorstellung
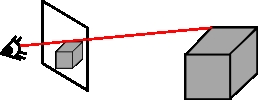
Die Griechen hatten eine etwas sonderbare Vorstellung vom Sehen: Sie stellten sich vor, daß aus ihren Augen Strahlen kommen, die dann auf die Umgebung treffen und dann quasi Nachricht an das Auge geben, was sie gesehen haben, wie weit weg es ist und welche Farbe es hat. Das ist in etwa das, was auch ein Raytracer macht. Wir wollen das also ersteinmal im Hinterkopf behalten und uns zuerst mit Strahlen einmal genauer auseinandersetzen. Danach werden wir Kugeln mit diesen Strahlen schneiden und eine passende perspektivische Kamera entwerfen. Schließlich werden wir einen sehr einfachen Raytracer schreiben, und ihn anschließend noch Ebenen als Objekte näherbringen, weil Kugeln alleine doch etwas langweilig sind.
Strahlen
Was ist also ein Strahl? Ein Strahl hat einen Ursprung, an dem er beginnt, und eine Richung, in die er Verläuft. Wer in der Schule in Geometrie aufgepasst hat, kennt dieses Objekt sicher auch noch als Halbgerade. Da wir später damit rechnen werden, müssen wir den Strahl in eine schöne Formel packen:
Die Punkte auf unserem Strahl R sind also parametrisiert durch t, welches die Zahlen von 0 bis unendlich durchläuft. Der Ursprung des Strahles ist o und seine Richung d. Somit kennen wir alle Punkte auf dem Strahl. Um nun zu prüfen, ob ein Strahl nun ein Objekt trifft, beginnen wir bei t = 0 und laufen alle Punkte ab, bis wir bei t = unendlich angekommen . . . Nein so machen wir das natürlich nicht funktionieren würde es zwar, es würde aber unendlich lange dauern: Nicht gerade das, was wir uns unter schnell vorstellen.
Bevor wir weitermachen, sollten wir unseren Strahl gleich noch in etwas Code verpacken, schließlich wollen wir uns ja einen Ray-Tracer schreiben:
public struct Ray
{
public Vertex3 Or igin ;
public Vertex3 Di r e c t i on ;
public Vertex3 Evaluate (double t )
{
return Origin + t * Direction ;
}
}
Zurück zu unserem Problem: Wir müssten also unendlich lange darauf warten, bis unser Ray-Tracer das Objekt gefunden hat, mit dem sich der momentan betrachtete Strahl schneidet. Viel schneller geht die Sache, wenn wir vorher beschließen, welche Objekte wir anzeigen können wollen. Für den Anfang wollen wir uns mit sehr einfachen Objekten begnügen: Kugeln. Sie sind schnell berechnet und werden für erste Experimente ausreichen.
Kugeln
Erinnerung: Eine Kugel ist definiert durch ihren Mittelpunkt und ihren Radius r. Setzt man den Mittelpunkt auf den Ursprung des Koordinatensystems, dann sind die Punkte auf der Oberfläche O unserer Kugel gerade die Punkte, die vom Ursprung den Abstand r haben. Die uns interessierende Bedingung wird so zu ||p|| = r für Punkte p in O. Die Gleichung kann man schadlos quadrieren und statt der Vektorlänge ||p|| bekommt man das ohne Wurzel ziehen zu berechnende Skalarprodukt von p mit sich selbst:
Setzt man hierein die obige Gleichung für den Strahl, ergibt sich:
Und damit:
Da die Richtung o und d unseres Strahls bekannt sind, haben wir eine quadratische Gleichung vor der Nase, die wir mittels Mitternachsformel lösen können:
Anhand der Diskriminante D, also dem Teil des obigen Ausdrucks, der unter der Wurzel steht, können wir entscheiden, ob der Strahl die Kugel trift. Ist nämlich D < 0, so kann man in den reelen Zahlen die Wurzel nicht berechnen. Ist D = 0, so gibt es genau eine Lösung der Schnittgleichung und für D > 0 schneidet der Strahl die Kugel genau 2 mal. Da wir unseren Strahl nur für positive Parameter t definiert haben, sollten wir die errechneten Schnittpunkte t1 und t2 noch daraufhin untersuchen:
public double RayIntersect ( Ray ray )
{
double boundingSquare = sphereRadius * sphereRadius ;
ray.Origin -= Position;
double a, b, c;
a = ray.Direction.DotDot ;
// DotDot ^= Skalarprod mit sichselbst : <d , d>
b = 2 * ( ray.Origin * ray.Direction );
// * ^= normales Skalarprod
c = ray.Origin.DotDot - boundingSquare;
double t1 , t2 ;
int roots = CalcQuadricRoots (a , b, c, out t1, out t2) ;
if (roots > 0)
return t1 >= 0 ? t1 : t2 ;
// kleinsterpositiver pos. Wert aus t1 , t2
else
return -1; // Kein Schnittpunkt
}
Einen kleinen Haken hat die Sache jedoch: Analytisch (d.h. per Stift und Papier) lässt sich mit der Mitternachtsformel wunderbar rechnen. Am Computer neigt sie zu Fehlern, was ganz allein an dem +- liegt. So führt man verlässlich eine Subtraktion durch, wenn D > 0 ist und Subtraktionen sind reines Gift für die Genauigkeit bei numersichen Rechnungen. Durch kleine Umformungen und das bestimmen eines Vorzeichens, können wir das Problem umgehen:
Quadratische Gleichungen
Hat man also eine Quadratische Gleichung in der allgemeinen Form:
dann bestimmt man die Nullstellen am besten durch:
Bei der Auswertung von q wird so sicherlich echt addiert, weil zu b eine Zahl gleichen Vorzeichens summiert wird. Dass der Wert für t1 stimmt, hat man dann auch sehr leicht nachgerechnet, wohingegen t2 in wildes rumgeschiebe der Formel ausartet und sich erst recht spät sign(b) herauswerfen lässt. Ein bischen Quellcode hierzu:
public static int CalcQuadricRoots(double a, double b, double c, out double x1, out double x2)
{
double determinant = b * b - 4 * a * c;
if (determinant < 0)
{
x1 = 0.0;
x2 = 0.0;
return 0;
}
determinant = Math.Sqrt(determinant);
double q = -0.5 * (b + PSgn(b) * determinant);
// Psgn: gives - 1 if b < 0 and 1 if b >= 0.
// so no zero as normal sgn would give us.
x1 = q / a;
x2 = c / q;
// Sort by value
if (x1 > x2)
{
q = x2; x2 = x1; x1 = q;
}
return x1 == x2 ? 1 : 2;
}
Die Funktion speichert die Nullstellen in den Variablen x1, x2 dem Wert nach sortiert ab und gibt die Anzahl der Nullstellen zurück. Da wir jetzt bereits bestimmen können, wo und wie oft unser Strahl die Kugel trift, können wir, nachdem wir uns noch einen Strahlenwerfer, (also eine Kamera) konstruiert haben, unseren ersten Ray-Tracer bauen.
Perspektivische Kamera
Einfacher Raycaster
Ebenen
Vorschau
Damit sind wir auch schon wieder soweit. Die ersten Grundlagen sind abgehandelt aber wirklich überzeugt sind wir vom Raytracing noch nicht. Damit sich das ändert, ist ein weiteres Tutorial in Planung: Wir wollen uns dann mit Licht und Normalen beschäftigen. Ausserdem sind Reflektionen und Transparenz spannende Dinge, denen wir uns widmen können. Wir wollen ausserdem unsere Objekte transformieren, scheeren, rotieren, ... Es bleibt also noch einiges im Bereich Raytracing zu tun, was hier nicht behandelt werden konnte.
Bis es soweit ist, könnt ihr euch ja selbst schonmal ein paar Gedanken zu dem Thema machen.
Benutzer:Nico Michaelis