Tutorial Terrain2
Inhaltsverzeichnis
Heightmap Texturen
Vorwort
Hi,
dies ist ein weiteres Tutorial zu Heightmaps. Ich verrate euch heute, wie man Heightmaps ein paar sehr interessante Texturen verpasst. Der erste Teil besteht darin, eine Procedural Texture zu erstellen, die eine Kombination aus der Heightmap und Bodentexturen ist, z.B. werden die hochsten Punkte der Landschaft mit Schnee bedeckt sein, niedrigere mit Stein, Gras und zum Schluss Wasser.
Der zweite Teil besteht dann darin, eine Lightmap zu Rendern. Sie enthalt die Lichtintensitat der einfallenden Sonne auf der Karte. Damit ihr wisst, wofur die Muhen dieser Aktion sind, hier einmal ein Bild der kombinierten Procedural Texture und Lightmap im Programm des letzten Tutorials(Um die Anzeige von Bodentexturen erweitert):
|
Besonders zu beachten: Die Landschaft wirft Schatten auf sich selbst |
Der Trick der Procedural Textures
Wollen wir uns zuerst einmal den Procedural Textures widmen. Die Idee dahinter ist folgende:
Wir haben eine Heightmap. Wir wollen uber diese eine Textur ziehen. Je nach Hohe soll eine andere Grundtextur gewahlt werden, z.B. Hohenstufe 0 Unterwassertextur. Stufe 60 Sand, Stufe 100 Gras, 170 Stein und 255 Schnee. Daneben wollen wir erreichen, dass die Texturen fliesend ineinander ubergehen. Dies erreichen wir, indem wir immer genau zwischen zwei Stufen die Farbwerte linear interpolieren. Die Grundtexturen werden gekachelt, damit sie nicht so gros sein mussen, wie die Heightmap selbst.
Ich habe folgende Texturen verwendet:
|
|
|
|
|
| Stufe: 0 | Stufe: 60 | Stufe: 100 | Stufe: 170 | Stufe: 255 |
|
|
Wenn ihr selbst Texturen erstellen wollt, zeichnet einfach drauf los, und lasst dann einen der Kachel Filter in Image Ready(Photoshop) daruber laufen. Ich habe den Kaleidoskop-Kachel Filter benutzt. Jedes Andere Prog das aus bestehenden Bildern Kacheln machen kann, fuhrt naturlich auch zum Erfolg. Allen die mehr von Texturen machen verstehen, bleibt es naturlich selbst uberlassen, dies mit Hand zu tun aber darin bin ich einfach nicht gut genug. Eine andere Moglichkeit besteht darin, auf einem Torus zu zeichen(das Prog dazu werdet ihr wohl selbst schreiben mussen :-(). |
Bevor wir unsere Textur rendern konnen, mussen wir uns eine Umgebung schaffen. Wir brauchen eine geladene Heightmap und die Grundtexturen:
type
TProcTexStage = record
Image : TImage;
ScrollBox : TScrollBox;
Stage : Byte;
StageLabel : TLabel;
end;
...
HeightMap : TBitMap;
ProceduralTex : TBitMap;
ProcTexs : Array of TProcTexStage;
...
Der Typ TProcTexStage beinhaltet je eine Grundtextur, geladen in der Image Komponente. Die jeweilige Hohenstufe ist in Stage abgelegt. Die restlichen Objekte sind nur fur das Utility das ich zum erstellen von Texturen geschrieben habe gedacht und haben keine weitere Bedeutung fur den Algorithmus selbst. Die Variable ProcTexs enhalt mehrere TProcTexStages. Sie sind bereits nach Stufen sortiert, beginnend mit der kleinsten, wobei gilt: Die niedrigste Stufe ist immer 0, die Hochste immer 255 (wird spater wichtig). Die Mindestzahl der Elemente ist demnach 2. Mehr ist kein Problem, unterschiedliche TProcTexStage sollten aber niemals die selbe Stufe haben.
Sobal diese Kriterien erfullt sind, konnen wir beginnen jedem Pixel der ProceduralTex einen neuen Farbwert zuzuweisen. Das Grundgerust ist wie folgt:
...
var
X,Y, HeightMapHeight : LongInt;
...
begin
//Texturen sind bereits sortiert...
if Length(ProcTexs) < 2 then
Exit;
//Größe anpassen
ProceduralTex.Width := HeightMap.Width;
ProceduralTex.Height := HeightMap.Height;
for X := 0 to HeightMap.Width - 1 do
for Y := 0 to HeightMap.Height - 1 do
begin
HeightMapHeight :=
Trunc((HeightMap.Canvas.Pixels[X,Y]/clWhite)*255);
//Farbwert zuweisen
...
end
end;
Da wir die Stufen nicht auf bestimmte Werte festgelegt haben (z.B. alle 64 Hohenwerte eine Stufe) mussen wir zunachst das Intervall finden, in welchem die aktuelle Stufe liegt. Die jeweils niedrigere Textur wird in einer variable Lower abgelegt, die hohere in Upper. Daneben benotigen wir noch einen Satz weiterer Variablen:
var
...
I : Integer;
Upper, Lower : LongInt;
LevelDifference : LongInt; //Levelunterschied zw. Upper u. Lower
LowerDifference : LongInt; //Abstand HeightmapHeight - Lower
LowerRGB, UpperRGB : TRGB; //RGB werte von Upper Lower
Prozent : Single; //Prozent der eingesetzten Farbwerte
FinalRGB : TRGB; //End RGB Wert
...
HeightMapHeight := Trunc(
(HeightMap.Canvas.Pixels[X,Y]/clWhite)*255);
Upper := 0;
Lower := 0;
//Intervall suchen, das für diese Höhenstufe interessant ist
for I := 1 to Length(ProcTexs)-1 do
if HeightMapHeight <= ProcTexs[I].Stage then
begin
Upper := I;
Lower := I -1;
Break
end;
Assert(Upper <> 0);
LevelDifference := ProcTexs[Upper].Stage - ProcTexs[Lower].Stage;
LowerDifference := HeightMapHeight - ProcTexs[Lower].Stage;
Assert(LevelDifference <> 0);
Prozent := LowerDifference / LevelDifference;
...
Der verwendete Typ TRGB ist ein Array[0..2] of Byte. Wenn ein TColor Wert als Ausgangsmaterial dient, wird dieser mithile folgender Funktion in ein TRGB umgewandelt:
procedure MakeRGB(Color : TColor; var RGB : TRGB);
begin
Move(Color, RGB[0], 3)
end;
Damit haben wir's fast geschafft. Das einzige was noch fehlt ist die lineare Interpolation zwischen den Farbwerten der Upper und Lower Textur. Dies ist aber an sich nicht weiter schwierig. Man denke an den Mathematikunterricht zuruck und erinnert sich an folgende gleichung: y= m * x + t, wobei m die Steigung und t der y-Achsenabschnitt ist:
...
Prozent := LowerDifference / LevelDifference;
MakeRGB(ProcTexs[Lower].Image.Canvas.
Pixels[X mod ProcTexs[Lower].Image.Width,
Y mod ProcTexs[Lower].Image.Height],LowerRGB);
MakeRGB(ProcTexs[Upper].Image.Canvas.
Pixels[X mod ProcTexs[Upper].Image.Width,
Y mod ProcTexs[Upper].Image.Height],UpperRGB);
for I := 0 to 2 do
FinalRGB[I] := Trunc(
(UpperRGB[I] - LowerRGB[I])*Prozent +
LowerRGB[I]);
// y = ( m )* x + t
ProceduralTex.Canvas.Pixels[X,Y] := RGB(FinalRGB[0],
FinalRGB[1],
FinalRGB[2])
Zum Einsatz kam folgende Heightmap:
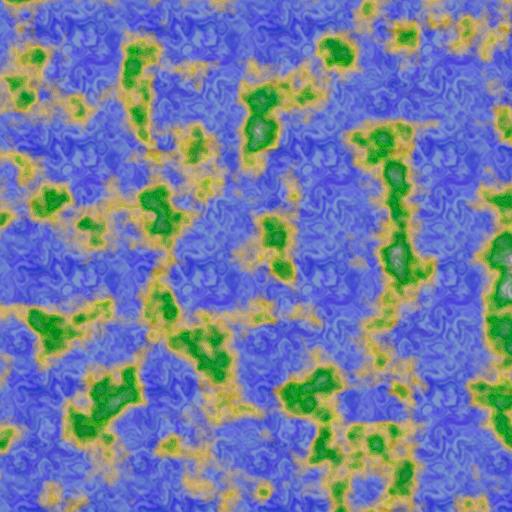
Jede andere funktioniert naturlich auch, wie z.B. die, aus meinem letzten Tutorial. Der Algorithmus liefert zusammen mit den Oben gezeigten Grundtexturen dieses Bild:
Das Spiel von Licht und Schatten
Wir konnten damit jetzt unsere Welt uberziehen. Was dann aber noch fehlt ist Beleuchtung und Schatten. Wir wollen hier Ambient Light und Diffuse Light zum Einsatz kommen lassen. Die Typische Formel zum Berechnen ist:
Intensity=Ambient + Diffuse * (L ?N)
L ist ein Vektor zur Lichtquelle, N die Flachennormale. Ambient und Diffuse die Starken der jeweiligen Lichttypen. Wir wollen wieder einmal alle Punkte der Heightmap durchgehen und unser Ergebnis in LightMaptex ablegen. Wenn ein Punkt nicht im Schatten eines anderen liegt, wird sein Farbwert mithilfe obiger Formel berechnet, ansonsten bekommt der Punkt den Farbwert des Ambient Light zugewiesen.
Die Normal Map
Bevor wir loslegen konnen, mussen wir eine Normal Map berechnen, deren Inhalt alle Normalen der Heightmap sind. Diese Komprimieren wir gleich auf Bytes, damit sie nicht Unmengen an Platz beansprucht. Leider kann man die Normalen nur schlecht fur einzelne Punkte direkt berechnen, wir mussen uns also Flachen zur Hilfe nehmen. Damit die Sache etwas runder wird, betrachten wir aber nicht nur eine Flache, sondern gleich alle anliegenden und berechnen daraus einen Normalendurchschnitt.
...
type
TNormalMap = Array of Array[0..2] of ShortInt;
...
procedure CreateNormalMap(HM : TBitMap; HeightScale : Single;
var NormalMap : TNormalMap);
begin
...
end;
...
var
NormalMap : TNormalMap;
HeightMapScale : Single;
NormalMap : TNormalMap;
begin
Sun[0] := Cos(LightRotation.Position*Pi/180);
Sun[1] := (LightHeight.Max - LightHeight.Position)/100;
Sun[2] := Sin(LightRotation.Position*Pi/180);
HeightMapScale := HeightScaleEdit.Value;
LightMapTex.Width := HeightMap.Width;
LightMapTex.Height := HeightMap.Height;
CreateNormalMap(HeightMap, HeightMapScale, NormalMap);
CreateLightMap(HeightMap, HeightMapScale, NormalMap, Sun, LightMapTex,
AmbientLight.Position / 100, DiffuseLight.Position/100,
RaytracingCheckBox.Checked)
end;
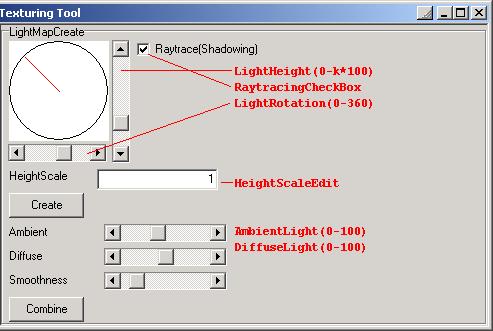
Dies stellt erst einmal ein Grundgerust dar. Statt einer einzelnen Beschreibung der einzelnen UI Komponenten folgendes Bild:
Nun also zur Funktion CreateNormalMap. Wie gesagt berechnen wir den Durchschnitt der Anliegenden Normalen. Folgendes Schaubild soll die verwendeten Flachen verdeutlichen, wobei v0 das derzeit betrachtete Vertex ist, alle anderen vxs anliegende:
v8
v7?--?--•v1
|8 /|1 /|
| / | / |
|/ 7|/ 2|
v6?-v0---•v2
|6 /|3 /|
| / | / |
|/ 5|/ 4|
v5?--?--•v3
v4
Mit dem Vektor Kreuzprodukt werden die Normalen fur die 8 Flachen berechnet, die dann zusammengezahlt und normalisiert werden, um den Durchschnitt zu erhalten, der in der Normal Map abgelegt wird:
procedure CreateNormalMap(HM : TBitMap; HeightScale : Single;
var NormalMap : TNormalMap);
const
VertexPoss : Array[0..8] of Array[0..1] of ShortInt =
((0,0),(1,-1),(1,0),(1,1),(0,1),(-1,1),(-1,0),(-1,-1),(0,-1));
Faces : Array[0..7] of Array[0..2] of Byte =
((0,1,8),(0,2,1),(0,4,2),(4,3,2),(0,5,4),(0,6,5),(0,8,6),(8,7,6));
var
X,Z : LongInt;
I : LongInt;
Vertieces : Array[0..8] of TVertex;
Normals : Array[0..7] of TVertex;
begin
SetLength(NormalMap, HM.Width*HM.Height);
FillChar(Vertieces[0,0], SizeOf(Vertieces), 0);
for Z := 0 to HM.Height - 1 do
for X := 0 to HM.Width - 1 do
begin
//Vertieces holen
for I := 0 to 8 do
begin
Vertieces[I][0] := X + VertexPoss[I][0]*VertexPosMultiply;
Vertieces[I][2] := Z + VertexPoss[I][1]*VertexPosMultiply;
Vertieces[I][1] := HM.Canvas.Pixels[X + VertexPoss[I][0], Z +
VertexPoss[I][1]]
/clWhite*255*HeightScale
end;
//Normalen holen
for I := 0 to 7 do
begin
Normals[I] := VectorCrossProduct(
VectorNormalize(VectorSubtract(Vertieces[Faces[I][0]],
Vertieces[Faces[I][1]])),
VectorNormalize(VectorSubtract(Vertieces[Faces[I][1]],
Vertieces[Faces[I][2]])));
Normals[I] := VectorNormalize(Normals[I])
end;
//Den "Durchschnittsvektor"...
for I := 1 to 7 do
Normals[0] := VectorAdd(Normals[0], Normals[I]);
Normals[0] := VectorScale(VectorNormalize(Normals[0]),127.0);
NormalMap[Z*(HM.Height) + X][0] := Trunc(Normals[0][0]);
NormalMap[Z*(HM.Height) + X][1] := Trunc(Normals[0][1]);
NormalMap[Z*(HM.Height) + X][2] := Trunc(Normals[0][2])
end
end;
Es werde Licht
Jetzt sind wir soweit. Wir konnen jetzt mit Hilfe unserer Formel fur jeden Punkt die Beleuchtung berechnen. Wie immer: Alle Punkte durchgehen, berechnen:
procedure CreateLightMap(HM : TBitMap; HeightMapScale : Single;
NormalMap : TNormalMap; Sun : TVertex; LightMap : TBitMap;
LightAmbient, LightDiffuse : Single; Raytracing : Boolean);
type
TRay = record
Origin, Direction : TVertex
end;
var
HeightMapData : Array of Array of byte;
procedure PrecacheHeightmap;
var
X,Z : LongInt;
begin
//Läd die Heightmap in ein Delphi Array
SetLength(HeightMapData, HM.Width);
for X := 0 to Length(HeightMapData) -1 do
SetLength(HeightMapData[X], HM.Height);
for Z := 0 to HM.Height - 1 do
for X := 0 to HM.Width - 1 do
HeightMapData[X,Z] := Trunc(HM.Canvas.Pixels[X,Z]/clWhite * 255)
end;
function RayIntersected(Ray : TRay; HM : TBitMap;
HeightMapScale : Single):Boolean;
begin
Result := False;
end;
var
X,Z : LongInt;
Ray : TRay;
n : TVertex;
f : Single;
begin
if Raytracing then PrecacheHeightmap;
//Wir haben paraleles Licht, also bleibt der Richtungsvektor des
//Rays immer gleich
Ray.Direction := VectorNormalize(Sun);
for Z := 0 to HM.Height - 1 do
for X := 0 to HM.Width - 1 do
begin
Ray.Origin[0] := X;
Ray.Origin[1] := HM.Canvas.Pixels[X,Z]/clWhite*255*HeightMapScale;
Ray.Origin[2] := Z;
if RayTracing and RayIntersected(Ray, HM, HeightMapScale) then
f := LightAmbient
else begin
//Komprimierte Normale zurückverwandeln
n[0] := NormalMap[Z*(HM.Height) + X][0];
n[1] := NormalMap[Z*(HM.Height) + X][1];
n[2] := NormalMap[Z*(HM.Height) + X][2];
f := LightAmbient+LightDiffuse*(VectorDotProduct(
VectorNormalize(n),VectorNormalize(Ray.Direction)));
//Zuviel licht?
if f > 1.0 then f := 1.0;
if f < 0.0 then f := 0.0
end;
LightMap.Canvas.Pixels[X,Z] := RGB(Trunc(f*255),
Trunc(f*255),
Trunc(f*255))
end
end;
Argh.... Wieder so ein Monster an Code! Naja, kampfen wir uns der Reihe mach durch... In HeightMapData wird die Heightmap geladen, um schnelleren zugriff auf sie zu haben (zur Erinnerung an das 1. Tutorial: GDI Befehle sind arsch langsam). Die entstandenen Daten werden von RayIntersected verwendet um schneller ausfuhrbar zu sein (glaubt mir, hier ist das wirklich notig!). RayIntersected selbst gibt bisher immer False zuruck (wir werden das spater noch andern), was bedeutet, auf den derzeit betrachteten Punkt wird kein Schatten geworfen.
Bevor ich weitermache erlautere ich kurz das Prinzip von Ray Tracern (z.B.: POV-Ray). Ein Ray ist ein Strahl, der von einem bestimmten Punkt (Origin) losgeschickt, in eine bestimmte Richtung (Direction). Das Tracing, also das abgehen des Rays wird die Funktion RayIntersected fur uns machen.
Die Richtung des Rays ist fur alle Punkte gleich, da die Sonne zur Erde einen so grosen Abstand hat, sodass das Licht parallel einfallt. Wird ein Ray geschnitten, wird dem Punkt Origin der Wert des Ambient Light zugewiesen, ansonsten wird mit der vorhin vorgestellten Formel die starke des einfallenden Lichtes berechnet.
Dies ist noch nichts besonderes, denn OpenGL berechnet das Licht auf ahnliche Weise. Was noch fehlt sind die Schatten. Wollen wir also ein wenig uber RayIntersected nachdenken...
Schattenspiele
Wir haben also Ray. Der Einfachheit halber, gehen wir diesen immer ein Stucken weiter, schauen ob die Hohe der Heightmap groser ist als der Ray oder nicht, solange bis wir am Ende der Karte angelangt sind. Klingt simpel? Ist es auch.
function RayIntersected(Ray : TRay; HM : TBitMap;
HeightMapScale : Single):Boolean;
var
Position : TVertex;
Vor : TVertex;
begin
Result := False;
Position := Ray.Origin;
Vor := VectorNormalize(Ray.Direction);
Position := VectorAdd(Position, Vor);
while (Position[0] > 0) and (Position[0] < HM.Width - 1) and
(Position[2] > 0) and (Position[2] < HM.Height - 1) do
begin
if HeightMapData[Trunc(Position[0]), Trunc(Position[2])]*
HeightMapScale >= Position[1] then
begin
Result := True;
Break
end;
Position := VectorAdd(Position, Vor)
end
end;
Das entlanglaufen des Rays ist nich unbedingt Ideal gelost, aber es tut seinen Zweck. Starten wir einmal unseren nun fertigen Lightmap Generator und betrachten das Ergebnis:
Diese kann man dann mit der Procedural Texture verknupfen... Je Heller ein Punkt in der Lightmap ist, desto mehr wird von den Farben der Procedural Texture genommen:
Nachwort
Aha, du hast also durchgehalten *g*. Ich hoffe jetzt bald viele schone Landschaften mit Schatten zu sehen. Bin jetzt etwas geschafft vom vielen Tippen.
...have a lot of fun!
Nico Michaelis aka DelphiC
|
|
||
Vorhergehendes Tutorial: Tutorial_Terrain1 |
Nächstes Tutorial: Tutorial_Terrain3 |
|
|
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen. |
||
