Datei:InterpolationBsp3.PNG
Aus DGL Wiki
Version vom 5. November 2005, 00:56 Uhr von Lyr (Diskussion | Beiträge) (Beispiel für Interpolation mit gegebenen Tangenten (und natürlich Punkten). Mathematica Code für diese Grafik: E1 = t^3*(-2) + t^2*4 + t*(-1) + 2 S1 = Plot[ E1, {t, 0, 1}, Frame -> True, GridLines -> Automatic, PlotStyle -> Thickness[0.01]] S2)
InterpolationBsp3.PNG (500 × 309 Pixel, Dateigröße: 3 KB, MIME-Typ: image/png)
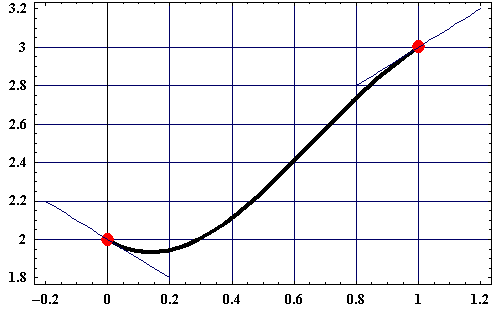
Beispiel für Interpolation mit gegebenen Tangenten (und natürlich Punkten). Mathematica Code für diese Grafik:
E1 = t^3*(-2) + t^2*4 + t*(-1) + 2
S1 = Plot[ E1, {t, 0, 1},
Frame -> True, GridLines -> Automatic, PlotStyle -> Thickness[0.01]]
S2 = ListPlot[{{0, 2}, {1, 3}}, PlotStyle -> {RGBColor[1, 0, 0],
PointSize[0.03]}]
Tangente1 = Plot[-1*t + 2, {t, -0.2, 0.2}, PlotStyle -> RGBColor[0, 0, 1]]
Tangente2 = Plot[1*t + 2, {t, 0.8, 1.2}, PlotStyle -> RGBColor[0, 0, 1]]
Show[S1, S2, Tangente1, Tangente2, TextStyle -> {FontFamily -> "Times",
FontSize -> 14, FontWeight -> Heavy}]
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 00:56, 5. Nov. 2005 |  | 500 × 309 (3 KB) | Lyr (Diskussion | Beiträge) | Beispiel für Interpolation mit gegebenen Tangenten (und natürlich Punkten). Mathematica Code für diese Grafik: E1 = t^3*(-2) + t^2*4 + t*(-1) + 2 S1 = Plot[ E1, {t, 0, 1}, Frame -> True, GridLines -> Automatic, PlotStyle -> Thickness[0.01]] S2 |
- Du kannst diese Datei nicht überschreiben.
Dateiverwendung
Diese Datei wird auf keiner Seite verwendet.