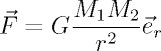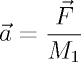GLSL Partikel 2
Der klassische Ansatz eines GPU Partikelsystems verwendet eine oder mehrere Texturen um die Partikel zu speichern. Zur Aktualisierung wird ein Quad in Größe dieser Textur gerendert. Der Fragmentshader liest die alten Daten aus einem Backbuffer und schreibt die aktualisierten Partikel in den Framebuffer. Dieses Verfahren ist an sich sehr effizient, hat aber einige Nachteile:
- Es ist sehr kompliziert effizient neue Partikel von der CPU zu emittieren. Die CPU muss immer wissen wo sich aktive Partikel in der Textur befinden. Sind die Lebensdauern der Partikel unterschiedlich (oder gar zufällig) wird dies zu einem echten Problem. In der Regel erfordert dies zumindest die Berechnung der Lebendauer zusätzlich auch auf der CPU durchzuführen, was natürlich nicht der Sinn eines GPU Partikelsystems ist.
- Da die Partikelanordnung wie gerade beschrieben fragmentiert, muss beim rendern der Partikel immer die vollständige Textur verarbeitet werden, auch wenn eigentlich nur wenige Partikel tatsächlich aktiv sind. Außerdem ist zum rendern ein großes VBO mit Dummy-Partikeln erforderlich, die eigentlich keine Daten enthalten.
- Sollen die Partikel zum Beispiel nach der Entfernung zur Kamera sortiert werden, ist dies sehr aufwendig. Auf der GPU verwendet man üblicherweise Odd-Even-Mergesort oder Bitonic-Sort. Beide Algorithmen vergleichen jeweils zwei Elemente und führen dann ggf. einen Tausch (Swap) dieser Elemente aus. Im Fragmentshader lässt sich jedoch die Position eines Fragments nicht mehr nachträglich ändern. Eine Implementierung im Fragmentshader erfordert also, dass jeder Vergleich zweimal durchgeführt wird. Das bedeutet auch, dass jeder Texturzugriff zweimal durchgeführt werden muss. Zudem erfordern beide Algorithmen sehr viele Passes. Für eine Million Partikel (1024²) sind so etwa 210 Passes erforderlich. Dies ist auch bei einer Verteilung über mehrere Frames nicht mehr sinnvoll in Echtzeit durchführbar.
Durch die Benutzung der Features aktueller Grafikhardware wie dem Geometryshader, Transform-Feedback, Instancing sowie diverser weiterer Features des Shader Model 4.0 lässt sich hier viel optimieren. Dieser Artikel setzt die Kenntnis dieser Funktionen voraus. Desweiteren sollte man natürlich wissen wie ein (state-preserving) Partikelsystem funktioniert, also zum Beispiel etwas mit den Begriffen Emitter und Forcefield anfangen können.
Inhaltsverzeichnis
Grundlagen
Ich verwende hier neben OpenGL 2.0 auch zahlreiche Extensions. Wenn man das Grundprinzip verstanden hat sollte es kein Problem sein diese Extensions durch eventuell verfügbare aktuellere Extensions zu ersetzen.
- GL_ARB_texture_float
- GL_EXT_texture_integer
- GL_EXT_texture_buffer_object
- GL_EXT_gpu_shader4
- GL_NV_transform_feedback
- GL_EXT_geometry_shader4
Zum speichern der Partikeldaten verwende ich mehrere Texturbuffer-Objects (TBO).
- ein 4x32bit-float Buffer zum speichern der Position und Größe des Partikels (GL_RGBA32F_ARB)
- ein weiterer 4x32bit-float Buffer zum speichern der Velocity und Lebenszeit des Partikels (GL_RGBA32F_ARB)
- ein 32bit-unsigned Buffer zum speichern des aktuellen Zufallsseed (GL_LUMINANCE32UI_EXT)
Alle Partikel werden durch Emitter erzeugt. Da uns später immer die genaue Anzahl der aktiven Partikel bekannt sein wird, müssen die Buffer nicht initialisiert werden.
Update
Das wichtigste an einem Partikelsystem ist immer der Update-Schritt. Daher fangen wir auch damit an. Auch wenn wir erst später erfahren wie neu erzeugte Partikel eigentlich in den Buffer kommen, nehmen wir zunächst einmal an die Buffer wären mit aktiven Partikeln gefüllt.
Eine Grafikkarte kann nicht aus einem Buffer lesen und gleichzeitig auch hinein schreiben. Wir benötigen also jeden Buffer doppelt: Einen Inputbuffer aus dem wir als VBO bzw. TBO lesen, während wir in den Outputbuffer via Transform-Feedback schreiben. Nach jedem Updateschritt werden die Rollen der Buffer getauscht.
Zunächst interpretieren wir den Position-Inputbuffer als Vertexbuffer und rendern sämtliche Partikel. Der Vertexshader ist trivial, denn die eigentliche Arbeit verrichtet der Geometryshader. Clipping und alles was danach in der Pipeline kommt wird nicht benötigt. Also insbesondere der Rasterizer und der Fragmentshader. Darum schalten wird diesen unnötigen Kram mit glEnable(GL_RASTERIZER_DISCARD_NV) einfach ab. Man sollte natürlich nicht vergessen das ganze später wieder einzuschalten.
Vertexshader:
void main() {
gl_Position = gl_Vertex;
}
Geometryshader:
#extension GL_EXT_gpu_shader4 : enable
#extension GL_EXT_geometry_shader4: enable
uniform samplerBuffer tboVelocity;
uniform usamplerBuffer tboRandom;
uniform float timeElapsed;
varying out vec4 velocity_out;
varying out unsigned int seed;
const vec3 wind = vec3(1.0, 1.0, 2.0);
vec3 constField() {
return timeElapsed * wind;
}
vec3 dampField(vec3 velocity, float strength) {
return -velocity*strength*timeElapsed;
}
vec3 noiseField(float strength) {
vec3 result;
seed = (seed * 1103515245u + 12345u); result.x = float(seed);
seed = (seed * 1103515245u + 12345u); result.y = float(seed);
seed = (seed * 1103515245u + 12345u); result.z = float(seed);
return timeElapsed * strength * ((result / 4294967296.0) - vec3(0.5,0.5,0.5));
}
void main() {
// get all particle data
vec3 position = gl_PositionIn[0].xyz;
float size = gl_PositionIn[0].w;
vec4 tmp = texelFetchBuffer(tboVelocity, gl_PrimitiveIDIn);
vec3 velocity = tmp.xyz;
float lifetime = tmp.w;
// update lifetime and discard dead particles
lifetime -= timeElapsed;
if (lifetime <= 0.0) { return; }
// update position and size
position += velocity * timeElapsed;
size += 0.3 * size * timeElapsed;
// read current random seed
seed = texelFetchBuffer(tboRandom, gl_PrimitiveIDIn).x;
// update velocity by applying force fields
velocity += dampField(velocity, 0.5);
velocity += constField();
velocity += noiseField(1.0);
// write vertex
gl_Position = vec4(position, size);
velocity_out = vec4(velocity, lifetime);
EmitVertex();
}
Da wir GL_POINTS rendern ist ein Primitiv genau einen Vertex groß. Aus diesem Grund eignet sich die eingebaute Variable gl_PrimitiveIDIn perfekt als Arrayindex. Via TexelFetch können wir also Velocity, Lebenszeit und aktuellen Seed auslesen.
Ist die Lebenszeit eines Partikels abgelaufen, brechen wir die Verarbeitung dieses Partikels ab. Die Funktion EmitVertex() wird also nicht aufgerufen und der Partikel somit unterdrückt. Der entscheidende Vorteil von Transform-Feedback an dieser Stelle ist nun, das beim schreiben in den Outputbuffer keine Lücke entsteht. Es tritt also keine Fragmentierung auf. Am Ende des Updatevorgangs befinden sich alle Partikel aufgeräumt am Anfang des Buffers. Mit einem Query lässt sich auch die Anzahl der in den Outputbuffer geschriebenen Partikel auslesen, beim nächsten Frame wissen wir also exakt wie viele Partikel wir rendern müssen.
Bezüglich des verwendeten Zufallsgenerators in der Funktion noiseField(float) sollte man bei Bedarf den Artikel GLSL Noise konsultieren. Der Rest des Update-Shaders sollte eigentlich klar sein.
Via Transform-Feedback werden die Inhalte gl_Position und den beiden varyings velocity_out und seed in ihre jeweiligen Outputbuffer geschrieben.
Emitter
Nachdem wir nun den Update-Schritt erledigt haben, stellt sich die Frage wie den nun eigentlich neue Partikel ins System kommen sollen. Dank Transform-Feedback geht dies überraschend einfach. Wir brauchen keine Fragmentierung oder ähnliches beachten, sondern einfach nur die Daten der neuen Partikel ans Ende der jeweiligen Buffer schreiben.
Wir könnten natürlich glBufferSubData benutzen, aber da nicht genau wissen wie viele Partikel gerade aktiv sind, wissen wir nicht in welchen Bereich geschrieben werden muss. Natürlich könnte man jetzt einen Query benutzen um die Anzahl der via Transform-Feedback geschriebenen Partikel zu ermitteln, aber da wir sowieso schon alles eingerichtet haben können wir die neuen Partikel auch einfach rendern.
Während Transform-Feedback aktiv ist, ist es nicht erlaubt den Shader zu wechseln. Aus diesem Grund verwenden wir einfach weiter unseren Update-Shader, wobei wir die Uniform timeElapsed auf 0 setzen. So werden zwar einige unnötige Berechnungen durchgeführt, aber normalerweise emittiert man sowieso nur einige 100 Partikel pro Frame. Wie die Partikel dann letztlich genau gerendert werden ist daher nur von geringer Bedeutung. Ich verwende hier zunächst mehrere std::vector um die nach und nach von der Physik und Spiellogik erzeugten Partikel zu sammeln. Einmal pro Frame werden diese dann in Buffer-Objekte geschrieben.
Sollte die maximale Größe der Partikelbuffer überschritten werden, werden die folgenden Partikel von Transform-Feedback stillschweigend unterdrückt. Um im nächsten Frame zu wissen wie viele Partikel aktiv sind, verwenden wir einen Query. Hier nun der Code zum aktualisieren der alten und emittieren der neuen Partikel.
void CParticleSystem::update(double dTimeElapsed) {
// flip buffers
int input = m_flip;
int output = m_flip = (1 - m_flip);
// setup shader
glUseProgram(m_prgMove);
glUniform1f(m_locMoveTimeElapsed, (float)dTimeElapsed);
// setup transform feedback
glBindBufferBaseNV(GL_TRANSFORM_FEEDBACK_BUFFER_NV, 0, m_vboPosition[output]);
glBindBufferBaseNV(GL_TRANSFORM_FEEDBACK_BUFFER_NV, 1, m_vboVelocity[output]);
glBindBufferBaseNV(GL_TRANSFORM_FEEDBACK_BUFFER_NV, 2, m_vboRandom[output]);
GLint locations[3] = { m_locMovePosition, m_locMoveVelocity, m_locMoveSeed };
glTransformFeedbackVaryingsNV(m_prgMove, 3, locations, GL_SEPARATE_ATTRIBS_NV);
glEnable(GL_RASTERIZER_DISCARD_NV);
glBeginQuery(GL_TRANSFORM_FEEDBACK_PRIMITIVES_WRITTEN_NV, m_qryWritten);
glBeginTransformFeedbackNV(GL_POINTS);
// draw active particles
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_BUFFER_EXT, m_tboRandom[input]);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_BUFFER_EXT, m_tboVelocity[input]);
glBindBuffer(GL_ARRAY_BUFFER, m_vboPosition[input]);
glVertexPointer(4, GL_FLOAT, 0, 0);
glEnableClientState(GL_VERTEX_ARRAY);
glDrawArrays(GL_POINTS, 0, m_active);
// draw newly emitted particles
if (m_emitted > 0) {
glUniform1f(m_locMoveTimeElapsed, 0.0f);
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_BUFFER_EXT, m_tboRandomEmit);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_BUFFER_EXT, m_tboVelocityEmit);
glBindBuffer(GL_ARRAY_BUFFER, m_vboPositionEmit);
glVertexPointer(4, GL_FLOAT, 0, 0);
glDrawArrays(GL_POINTS, 0, m_emitted);
m_emitted = 0;
}
// clean up transform feedback, retrieve count of processed particles
glEndTransformFeedbackNV();
glEndQuery(GL_TRANSFORM_FEEDBACK_PRIMITIVES_WRITTEN_NV);
glGetQueryObjectuiv(m_qryWritten, GL_QUERY_RESULT, &m_active);
// clean up
glDisableClientState(GL_VERTEX_ARRAY);
glDisable(GL_RASTERIZER_DISCARD_NV);
glBindBuffer(GL_ARRAY_BUFFER, 0);
glUseProgram(0);
}
Rendern
Ein Partikelsystem ist natürlich sinnfrei, wenn die Partikel nicht auch irgendwie dargestellt werden. Das ganze ist nicht weiter kompliziert. Wir benötigen weder die Velocity, die Lebenzeit noch den aktuellen Zufallsseed. Daher können wir einfach den Position-Buffer als Vertexbuffer rendern. Die Methode render() und die verwendeten Shader sollten selbst erklärend sein.
void CParticleSystem::render(CVector3f vEye) {
int input = m_flip;
// setup shader
CVector2i viewport = CViewerWidget::instance()->getViewport();
glUseProgram(m_prgRender);
glUniform3f(m_locRenderEye, vEye.x, vEye.y, vEye.z);
glUniform1f(m_locRenderViewport, viewport.y);
// setup vbo, tbo's, etc.
glEnable(GL_VERTEX_PROGRAM_POINT_SIZE);
glEnable(GL_POINT_SPRITE);
glTexEnvf(GL_POINT_SPRITE, GL_COORD_REPLACE, GL_TRUE); // generate TexCoords automatically
glDisable(GL_ALPHA_TEST);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
glDepthMask(GL_FALSE);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, m_texParticleAlpha);
glBindBuffer(GL_ARRAY_BUFFER, m_vboPosition[input]);
glVertexPointer(4, GL_FLOAT, 0, 0);
glEnableClientState(GL_VERTEX_ARRAY);
// draw all active particles
glDrawArrays(GL_POINTS, 0, m_active);
// clean up
glDisableClientState(GL_VERTEX_ARRAY);
glDepthMask(GL_TRUE);
glDisable(GL_BLEND);
glDisable(GL_POINT_SPRITE);
glDisable(GL_VERTEX_PROGRAM_POINT_SIZE);
glBindBuffer(GL_ARRAY_BUFFER, 0);
glUseProgram(0);
}
Vertexshader:
uniform vec3 eye; // camera position
uniform float viewportHeight;
varying float alphaScale;
void main()
{
vec4 position = vec4(gl_Vertex.xyz, 1.0);
float size = gl_Vertex.w;
// transform position
gl_Position = gl_ModelViewProjectionMatrix * position;
// calculate pointsize
gl_PointSize = (viewportHeight * size) / distance(position.xyz, eye);
// rendering particles with size 0.0 may result in undefined behaivor
gl_PointSize = clamp(gl_PointSize, 0.01, 64.0);
// derive an alpha value from particle size
alphaScale = clamp(0.05 / size, 0.001, 0.2);
}
Fragmentshader:
uniform sampler2D texAlpha;
varying float alphaScale;
const vec3 color = vec3(0.384, 0.343, 0.286);
void main()
{
float alpha = texture2D(texAlpha, gl_TexCoord[0].xy).a * alphaScale;
if (alpha < 0.0039) { discard; } // discard fragment when alpha smaller than 1/255
gl_FragColor = vec4(color, alpha);
}
Erweiterungen
Nun wollen wir das bestehende Partikelsystem erweitern. Es sollte klar sein das die hier beschriebenen Dinge sehr viel Rechenleistung benötigen. Diese Aktionen müssen also möglicherweise über mehrere Frames verteilt werden.
Partikel/Partikel-Interaktion
Es gibt diverse Effekte bei denen man eine direkte Interaktion der Partikel untereinander benötigt. Beispiele sind wirkende Gravitationskräfte zwischen den Partikeln, die Simulation von Luftdruck und ähnliches.
Da wir unsere Partikeldaten in Texturen (bzw. TBOs) gespeichert haben, ist eine solche Interaktion theoretisch leicht zu realisieren. Wir bauen im Update-Shader einfach eine Schleife über sämtliche anderen Partikel ein. Die Graviationskraft berechnet sich nach der folgenden Formel.
Dabei ist G die Graviationskonstante, M1 bzw. M2 die Masse und r der Abstand der beiden Partikel. Der Vektor er ist die normalisierte Richtung. Beschleunigung ist Kraft durch Masse, d.h. die Masse des betrachteten Partikels kürzt sich aus der Gleichung.
Im Beispiel werden einfach die Beschleunigungen zwischen den Partikeln berechnet und aufsummiert. Natürlich ziehen wir so viele Berechnungen wie möglich aus der Schleife hinaus.
// particle interaction, naive approach
const float GRAVITATION = 6.67428e-11; // gravitational constant
vec3 accum = vec3(0,0,0);
for (int i=0; i<particleCount; ++i) {
vec4 other = texelFetchBuffer(tboPosition, i); // other.xyz=Position, other.w=Mass
vec3 dir = other.xyz - position;
float len = length(dir);
if (len > 0.0001) {
accum += (other.w / len) * dir;
}
}
velocity += GRAVITATION * timeElapsed * accum;
Der aufmerksame Leser wird nun hoffentlich verzweifelt den Kopf geschüttelt haben, den der Aufwand für diese Aktion ist natürlich quadratisch. Bei einem kleinen Partikelsystem mag dies machbar sein, aber bei einer Million Partikel würden wir insgesamt eine Billion Iterationen der inneren Schleife benötigen. Nun, Grafikkarten sind schnell, aber nicht schnell genug um dies in Echtzeit zu erledigen.
Wir benötigten also eine andere Lösung. Es gibt prinzipiell drei verschiedene Ansätze, zumindest sind das die, die mir gerade einfallen.
- Verteilen der Operationen auf mehrere Frames. Dies macht nur bei mittelgroßen Partikelsystemen Sinn. Für ein doppelt so großes Partikelsystem muss man die Berechnung auf viermal so viele Frames verteilen um mit der gleichen Geschwindigkeit zu rendern. Das ist natürlich aussichtslos, da man immer noch quadratische Laufzeit hat.
- Verwendung einer Datenstruktur. Üblicherweise nimmt der Einfluss der Partikel untereinander mit der Entfernung ab. Eigentlich muss man daher nur die Partikel in der näheren Umgebung berücksichtigen. Rekursive Datenstrukturen wie Bäume sind auf der Grafikkarte schwer zu realisieren. Aber man könnte die Eigenschaft ausnutzen das die Partikel sortiert sind. Logischerweise muss man dann die Partikel dann zuerst einmal sortieren, was natürlich ebenfalls sehr aufwendig ist. Aber falls man die Partikel aus einem anderen Grund zum Beispiel nach der Entfernung zur Kamera sortiert hat sollte man dies ausnutzen.
- Randomisierte Algorithmen zeichnen sich meist durch ihre Einfachheit und Effizienz aus. Einen solchen Ansatz wollen wir im folgenden näher betrachten.
Randomisierung
Bei hundert tausenden Partikeln ist der Einfluss des einzelnen Partikels gering. Bei diesem Ansatz wählen wir jedes Frame eine neue zufällige Repräsentantenmenge von sagen wir 50 Partikeln. Das Ergebnis rechnen wir dann auf die gesamte Partikelwolke hoch. So erhalten wir eine Approximation der richtigen Lösung. Dies ist definitiv der schnellste Ansatz den die Laufzeit ist nur linear und die Qualität der Approximation lässt sich bequem über die Anzahl der Repräsentanten steuern.
Man kann die Repräsentantenmenge entweder für jeden Partikel einzeln im Shader generieren oder einmal für alle Partikel gleich als Uniform-Array (oder Textur) übergeben. Die zweite Variante hat den Vorteil, dass die Grafikkarte den Cache besser nutzen kann und man spart natürlich die Berechnung der Zufallszahlen im Shader. Dies sorgte in meinem Versuch für eine etwa 50% höhere Geschwindigkeit, wobei aber insgesamt weniger Partikel berücksichtigt werden und daher die Approximation auch etwas schlechter ist. Letztlich kommt es also ungefähr auf das gleiche hinaus.
Als Beispiel zeige ich hier einmal die erste Variante mit der auch der Screenshot rechts erzeugt wurde. Ich verwende hier wieder den Zufallsgenerator aus dem Artikel GLSL Noise.
// particle interaction, randomization approach
const float GRAVITATION = 6.67428e-11; // gravitational constant
const int REP_COUNT = 50; // number of representatives
vec3 accum = vec3(0,0,0);
for (int c=0; c<REP_COUNT; ++c) {
seed = (seed * 1664525u + 1013904223u);
int i = int(float(seed) / 4294967296.0 * particleCount);
vec4 other = texelFetchBuffer(tboPosition, i);
vec3 dir = other.xyz - position;
float len = length(dir);
if (len > 0.0001) {
accum += (other.w / len) * dir;
}
}
velocity += GRAVITATION * timeElapsed * (particleCount/float(REP_COUNT)) * accum;
Split und Merge
Da wir mit dem Geometryshader arbeiten, ist es problemlos möglich Split- oder Merge-Operationen auf die Partikel anzuwenden. Also beispielsweise könnten sich kollidierende Partikel vereinen. Ein Partikel bleibt dabei erhalten und vergrößert seine Masse auf die Summe beider Partikel. Die Bewegungsrichtung wird ebenfalls aus der Summe beider Partikel ermittelt. Der andere Partikel wird aus dem System entfernt, wie wir dies bereits vom Update-Shader im Grundlagen-Abschnitt kennen. Natürlich benötigt man irgendeine Konvention welcher der beiden Partikel erhalten bleibt und welcher entfernt wird, da man die Entscheidung natürlich für jeden der beiden Partikel einzeln treffen muss. Anbieten würde sich beispielsweise ein Vergleich der Position im Vertexbuffer (gl_PrimitiveIDIn).
Umgekehrt könnte ein Partikel in mehrere Teile zerfallen. Dies lässt sich leicht realisieren, der Geometryshader emittiert einfach entsprechend viele Partikel.
Sortieren nach Z
Verwendet man zum Beispiel additives Alpha-Blending ist die Reihenfolge in der die Partikel gerendert werden nicht von belang. Arbeitet man dagegen mit einer nicht-assoziativen Blending-Operation, beispielsweise der folgenden, muss man die Partikel eigentlich nach der Entfernung zur Kamera sortieren um ein korrektes Ergebnis zu erzielen.
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
Insbesondere wenn alle Partikel die gleiche Farbe und einen sehr geringen Alpha-Wert haben ist der Effekt des einzelnen Partikels nur sehr gering. In so einem Fall ist das Ergebnis ohne Sortierung zwar eigentlich falsch, aber man wird kaum einen Fehler entdecken. Auch hier kann man also auf die aufwendige Sortierung verzichten. Natürlich gibt es aber auch Fälle in denen man auf korrektes Rendering angewiesen ist. Das kann der Fall sein wenn man beispielsweise Feuer und Rauch in einem einzigen Partikelsystem verwaltet. Die Farben der Partikel unterscheiden sich stark. Nur mit einer Sortierung der Partikel lässt sich das korrekte Ergebnis erzielen.
Sofern das Partikelsystem auf der CPU läuft ist die Sortierung kaum ein Problem. Die Anzahl der Partikel ist gering, geeignete Algorithmen (z.B. Quick-Sort, Intro-Sort, ...) sind gut erforscht und in jeder guten Standardbibliothek implementiert. Bei einem GPU-Partikelsystem steht man dagegen vor einem Problem. Zum einen verwaltet man üblicherweise wesentlich mehr Partikel, zum anderen arbeitet die GPU parallel und es gibt keinen Random-Write-Access, d.h. die Standard-Algorithmen lassen sich nicht sinnvoll anwenden.
Trotzdem gibt es Algorithmen die es ermöglichen halbwegs effizient auf der GPU zu sortieren.
- Odd-Even Transition Sort, ein naiver, nicht praktikabler Ansatz, Laufzeit: O(N² / P)
- Odd-Even Merge Sort, Laufzeit: O((N log²N) / P)
- Bitonic Merge Sort, Laufzeit: O((N log²N) / P)
- Adaptive Bitonic Sort, Laufzeit: O((N log N) / P)
Bei den Angaben zur Laufzeit bezieht sich N auf die Anzahl der Partikel und P auf die Anzahl der parallel arbeitenden Shader-Einheiten.
Referenzen
- P. Kipfer und R. Westermann, GPU Gems 2, Chapter 46. Improved GPU Sorting, Technische Universität München, 2004
- Die Algorithmen Odd-Even Transition Sort, Odd-Even Merge Sort sowie Bitonic Merge Sort werden hier erklärt.
- A. Greß und G. Zachmann, GPU-ABiSort: Optimal Parallel Sorting on Stream Architectures, TU Clausthal, 2006
- Der Algorithmus Adaptive Bitonic Sort wir hier beschrieben.
- Bilardi, G. und Nicolau, Adaptive Bitonic Sorting: an Optimal Parallel Algorithm for Shared Memory Machines, Cornell University, 1986
- Brauchbarer mathematischer Beweis für die Aussagen über Bitonic-Sequenzen.
Transparente Schatten (mit Self-Shadows)
Referenzen
- T. Lokovic und E. Veach, Deep Shadow Maps, SIGGRAPH 2000 Proceedings, Addison-Wesley, August 2000
- C. Dachsbacher† und M. Stamminger, Translucent Shadow Maps, University of Erlangen-Nuremberg, 2003
Links
- Shader : Shader Grundlagen
- Tutorial GLSL : Einführung in GLSL
- GLSL Partikel : GPU-Partikelsystem mit älterer Hardware