Tutorial Software-Synthesizer
Inhaltsverzeichnis
- 1 Über Schall und Digitalisierung
- 2 Voreinstellungen
- 3 Der erste Ton
- 4 Die Schwebung
- 5 Andere Wellenformen
- 6 Hausgemachte Ober- und Untertöne
- 7 Hüllkurven oder Attack, Decay, Sustain, Release Envelopes
- 8 Ein paar synthetische Musikinstrumente
- 9 Oktaven, Halbtöne und was sonst dazugehört
- 10 Abschluss
Über Schall und Digitalisierung
Schall ist, wie sicherlich Jeder weis, nichts anderes als Druckschwankungen im uns umgebenden Medium: meist Luft. Aber er lässt sich auch gut durch Wasser oder Metall übertragen, nur vor dem Nichts, dem Vakuum, muss er kapitulieren. Die Druckschwankungen werden vom Trommelfell in unserem Ohr auf ein Knochensystem und von diesem auf das eigentliche Hörorgan übrtragen, welches über feine Haare die Druckschwankungen in Nervensignale übersetzt. Unser Gehirn bereitet die Daten auf, wobei ein subjektiver Eindruck entsteht - wir hören.
Dabei ist unser Ohr im Stande, unterschiedliche Frequenzen als solche einzeln wahrzunehmen. Das ist insofern etwas besonderes, da unser Auge genau das nicht kann. Treffen auf die Netzhaut gleich intensiv und gemeinsam blaues und gelbes Licht, so entsteht ein grüner Farbeindruck. Unser Ohr, würde es nicht auf Schall, sondern auf elektromagnetische Wellen reagieren, würde das Blau und das Gelb als solche einzeln identifizieren können. Manche Menschen haben im übrigen eine andere Sehstäbchenzusammensetzung auf der Netzhaut, als der "normale" Mensch - so empfinden einige das gemischte Computergelb als eine andere Farbe, als das "echte" Gelb.
Nun wollten wir uns aber nicht mit dem Sehen, sondern mit dem Hören beschäftigen. Um Schall zu digitalisieren und damit in Computertaugliche Form zu bringen, benutzt man Mikrofone. Diese besitzen eine Membran, die durch die Druckveränderungen der umgebenden Luft in Schwingung versetzt wird. An einer Stelle der Membran befindet sich eine Spule, in einem Magnetfeld. Wird die Membran durch Schall bewegt, wird die Spule im Magnetfeld bewegt: es entsteht ein Induktionsstrom, der nach Verstärkung ein elektrisches Signal liefert. Dieses Signal könnte man z.B. an einen Lautsprecher weiterleiten und so wieder vertonen.
In unserem Falle wollen wir die Signaldaten jedoch digitalisieren. Dazu wird ein Analog/Digitalwandler verwendet, der die unterschiedlichen Spannungen in Zahlenwerte umwandelt (digitalisiert). Das analoge Signal ist durchgängig, während digitale Daten immer nur kleine Abschnitte des Signals darstellen können, weshalb das Signal gesampelt wird: In einer Sekunde werden gleichverteilt die Signalpegel des analogen Signals in eine Reihe Zahlenwerte umgewandelt. Die Anzahl der Zahlenwerte pro Sekunde wird als Samplingrate bezeichnet. Audio CDs werden mit 44,1 kHz gesampelt, d.h. pro Sekunde wird das analoge Signal des Mikrofons 44100 mal in einen digitalen Wert, ein Sampel, übersetzt.
Wir wollen jedoch den umgekehrten Weg gehen: Wir wollen eine Reihe Sampels selbst erzeugen, um so wohlklingende Töne zu erzeugen, die wir dann als Sounds oder Musik in unseren Projekten einsetzen können. Bis dahin ist es ein längerer Weg. Lest das Tutorial nicht zu schnell, pausiert auch hin und wieder mal, damit ihr das gelernte ausprobieren könnt. Eigene Ideen können häufig auch sehr interessant klingendes hervorbringen. Probiert einfach mal ein wenig rum, aber denkt immer daran, dass, solltet ihr einmal nichts hören können, ein aufdrehen der Lautsprecher ungesund werden könnte. Bleibt mit dem Regler in den Bereichen, die ihr auch sonst nutzt.
Für viele der hier gezeigten Experimente ist hochwertiges Equipment zu empfehlen. Es kann durchaus sein, dass durch billige Boxen euch einige Erkenntnisse verwehrt bleiben, weil die Sache einfach nicht so klingt, wie sie soll. Da klappert mal etwas mit und schon verändert sich der Ton oder es entstehen zusätzliche, andersfrequente Töne, die den klaren Eindruck trüben. Die 5 Euro Boxen, die zum üblichen Komplettsystem gehören sind in keinem Fall geeignet. Auch eine ordentliche Soundkarte wäre zu empfehlen, wobei diese noch nicht einmal neu sein muss - auch eine alte Soundblaster AWE-32 wäre vollkommen ausreichend: nur hochwertig muss sie sein. Ach ja, eine 16-Bit Soundkarte sollte es dann schon sein ;-) Viele Onboard Soundkarten tuns auch, nur leider nicht alle :-(.
Voreinstellungen
Um direkt Töne aus den Boxen zu zaubern, werden wir uns der FMOD Bibliothek bedienen. Ich habe hier nicht vor, diese Bibliothek bis ins Kleinste zu erklären. Es dürfte genügen, wenn ihr euch die zugehörigen Tutorials anschaut. Zum Abspielen werden wir uns der Callbackfunktionalität der Bibliothek bedienen, d.h. FMOD ruft eine von uns definierte Funktion immer wieder auf. Diese wird dann die nächsten, gesampelten Daten zurückgeben, so dass diese dann auf der Soundkarte ausgegeben werden.
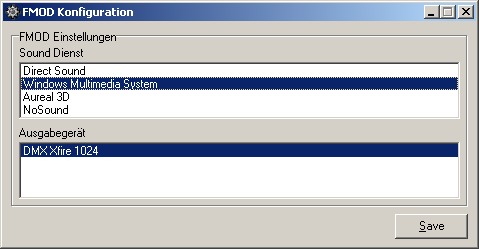
Da FMOD eine ganze Reihe Treiber für unterschiedliche Soundsysteme mitbringt, müssen ein paar Einstellungen getroffen werden. Damit das nicht bei jedem Programmstart geschieht, habe ich ein kleines Programm geschrieben, dass für alle der hier geschriebenen Programme entsprechende Voreinstellungen trifft und abspeichert. Bevor ihr weitermacht, startet einmal fmodconf, stellt das ganze eurem System entsprechend ein und drückt auf Save:
Der erste Ton
Der einfachste Ton, der von unserem Gehör als eindeutig nur zu einer Frequenz zugeordnet wird, lässt sich mit einer Sinuskurve beschreiben. Das gleiche erzeugen im übrigen auch gute Stimmgabeln, mit denen ihr sicherlich schon alle einmal im Physik- oder Musikunterricht Freundschaft schliessen konntet. Das ganze klingt sehr dünn, aber das ist genau das, was ich euch zeigen möchte.
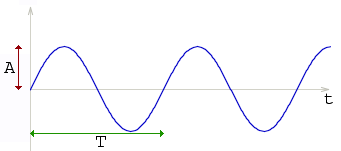
Zuerst sollten wir jedoch ein paar wesentliche Begriffe einer Welle klären:
Dieses Diagramm zeigt den durch ein gutes Mikrofon erzeugten Verlauf der Spannung auf der Zeit an, wenn eine angeschlagene Stimmgabel einen Ton erzeugt.
| Amplitude(A): Der Betrag des stärksten Ausschlags der Welle. Eine grössere Amplitude erzeugt einen lauteren Ton - und umgekehrt. |
| Periodendauer(T): Die Dauer einer vollständigen Schwingung. |
Frequenz: Die Zahl der vollständigen Schwingungen in einer Zeiteinheit. Sie wird üblicherweise pro Sekunde betrachtet:
|
| Schallgeschwindigkeit: Die Geschwindigkeit, mit der sich der Schall vorwärtsbewegt: 331 m/s in der Luft. |
| Wellenlänge: Ist die Länge einer Welle. Sie errechnet sich aus der Schallgeschwindigkeit geteilt durch die Frequenz. |
Nun wollen wir also eine Stimmgabel mit dem Computer simulieren. Alles was wir dazu machen müssen, ist eine Sinuskurve an FMOD zu übergeben. Wie bereits erklärt, wird eine Sekunde in eine Reihe Sampels zerlegt. Wir wollen mit einer Scrollbar die Frequenz des Tones einstellen können:
ssynth1:
var
Pos : Integer;
Freq : Integer;
function StreamCallback(Stream: PFSoundStream; Buff: Pointer; Len, Param: Integer): ByteBool; stdcall;
var
Count: Integer;
Buffer: PChar;
begin
Freq := SinGenForm.FreqBar.Position;
Buffer := PChar(Buff);
Count := 0;
while Count < (Len div 4) do { div 4 = 16bit stereo (4 bytes per sample) }
begin
PSmallInt(Buffer)^ := Trunc(Sin(2*Pi/SamplingRate*Freq*Pos) * (32767.0/2.0)); { Left channel }
Inc(Buffer, 2);
PSmallInt(Buffer)^ := Trunc(Sin(2*Pi/SamplingRate*Freq*Pos) * (32767.0/2.0)); { Right channel }
Inc(Buffer, 2);
Inc(Count);
Inc(Pos);
end;
Result := True;
end;
Die Variable Pos dient dem linearen Voranschreiten in unserer Sinuskurve. Durch das Teilen durch die Sampling-Rate erreichen wir, dass jede Sekunde ein Bereich von k bis k+1 durchlaufen wird, also ein Intervall der Länge 1: [0..1]+k; Wenn durch unsere Zählvariable jede Sekunde ein Bereich der Länge 1 durchlaufen wird, wird die Sache für uns viel einfacher. Durch die Multiplikation mit der Frequenz, wird dann nämlich ein Intervall von [0..Freq] durchlaufen und wir sind nahe dran an dem, was wir haben wollen. Wir müssen nur bedenken, dass der Sinus eine volle Schwingung im Bereich [0..2*Pi] beschreibt, also multiplizieren wir mit 2*Pi und erzeugen damit eine Sinus-Kurve, die in einer Sekunde Freq viele Schwingungen macht. Es wird Zeit zum Ausprobieren von synth1. Das Programm ist im im übrigen auf den Kammerton a: 440Hz voreingestellt - nur damit wir gleich mal den Bezug zur Musik herstellen. ;-)
Die Schwebung
Wir wollen unserer Stimmgabel eine weitere, gleichlaute Stimmgabel hinzufügen. Diese ist um wenige Frequenzteile verstimmt, so dass die Frequenzen wirklich sehr nahe beieinander liegen. Mit unserer Scrollbar wollen wir diesmal nicht einen großen Frequenzbereich abdecken, sondern nur eine Möglichkeit zum manipulieren des Anteils schaffen. Die Hauptfrequenz legen wir auf 880 Hz fest. Freundlicherweise genügt es, die zweite Stimmgabel durch Addition einer zweiten Sinuskurve hinzuzufügen - wir müssen nur darauf achten, dass wir dann in dem uns begrenzenden Werteintervall bleiben:
Bewegt man den Regler an den äusseren Rand, so nimmt man zwei erkennbar unterschiedliche Töne wahr. Kommt man der Mitte näher, verändert sich das Klangbild stark. Es entsteht eine art Pulsierender Ton. Dieser Effekt kommt häufig in Musikinstrumenten zum Einsatz, so hat jede Taste im Klavier drei zugehörige Saiten, die leicht gegeneinander verstimmt sind, so dass sie einen schwebungstypischen Klang erzeugen.
Wer will, soll einmal einen typischen Audioeditor starten, etwa den kostenlosen Audacity, und betrachte damit einmal den Funktionsgraphen. Einen derartigen Audioeditor solltet ihr für eure Versuche immer parat halten, um bei bedarf mal genau hinzusehen, was ihr da eigentlich erzeugt und ob das dem entspricht, was ihr euch vorgestellt habt.
ssynth2:
function StreamCallback(Stream: PFSoundStream; Buff: Pointer; Len, Param: Integer): ByteBool; stdcall;
var
Count: Integer;
Buffer: PChar;
Value : Single;
Delta : Single;
begin
Freq := 880;
Buffer := PChar(Buff);
Count := 0;
Delta := 1.0 + (1/10000.0 * SchwebGenForm.PercentBar.Position);
while Count < (Len div 4) do
begin
Value := (Sin(2*Pi/SamplingRate*Freq*Pos) + Sin(2*Pi/SamplingRate*Freq*Pos*Delta));
PSmallInt(Buffer)^ := Trunc(Value * (32767.0/2.0)); { Left channel }
Inc(Buffer, 2);
PSmallInt(Buffer)^ := Trunc(Value * (32767.0/2.0)); { Right channel }
Inc(Buffer, 2);
Inc(Count);
Inc(Pos);
end;
Result := True;
end;
Andere Wellenformen
Statt Sinusförmigen Wellen, bietet es sich an, pulsierende, dreieckige oder jegliche Arten anderer, (periodischer) Funktionen zu verwenden. Diese klingen dann teilweise etwas ungewöhnlich, aber wesentlich voller als der typische Sinuston. Dies liegt daran, dass, würde man die Graphen aus Sinuskurven nachbauen, so würde man die Sinus-Graphen aus ganzen Frequenzbändern benötigen, wodurch das gehörte Frequenzspektrum natürlich stark zunimmt. Der Effekt: Der Ton hört sich wesentlich voller an.
Ein wertvolles Hilfsmittel zur Analyse der dadurch "betonten" Frequenzbereiche ist die Fourier Analyse. FMOD bietet eine leicht zugängliche API, um eine ganze Reihe Frequenzbänder zu untersuchen. Das bedeutet für uns: Ab sofort benötigt jeder unserer Synthesizer ein Display zur Frequenzanalyse. Leider sind diese Analysen nie so recht perfekt, aber um einen Eindruck der belegten Frequenzen zu erhalten, genügt es allemal.
Sinus
Der altbekannte Sinus muss natürlich zum Vergleich wieder mit dabei sein:
ssynth3:
function SinWave(x: Single): Single;
begin
Result := Sin(2*Pi*x);
end;
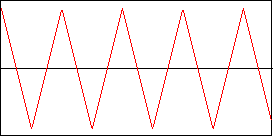
Dreieck
Das Dreieck klingt ähnlich wie der Sinus, nur ein wenig voller. Dass beide sehr verwand sein müssen, lässt sich ja bereits am Graphen erkennen.
ssynth3:
function DreieckWave(x: Single): Single;
begin
Result := Abs(frac(x) - 0.5) * 4 - 1;
end;
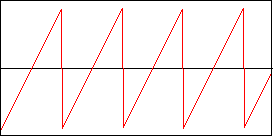
Sägezahn
Der Sägezahn klingt dann schon wesentlich voller und bissiger, aber macht euch am besten selbst ein Bild - man muss es gehört haben, um zu wissen wie es klingt ;-)
ssynth3:
function SaegezahnWave(x: Single): Single;
begin
Result := (-1 + 2 * frac(x));
end;
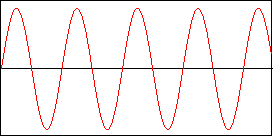
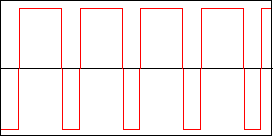
Puls
Der Puls schlägt dann schon sehr aus der Reihe. Durch Veränderunge der Länge der gleichartigen Bereiche, kann man den klang sehr gut und einfach manipulieren.
ssynth3:
function PulseWave(x: Single): Single;
function Sgn(x : Single) : Single;
begin
if x < 0 then
Result := -1.0
else
Result := +1.0;
end;
begin
Result := Sgn(frac(x) - IrgendwasZwischen0undEinhalbes);
end;
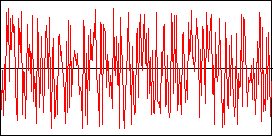
Rauschen
Nun, dieser Klang ist sehr charakteristisch und ich vermute jeder kennt ihn längst ;-) Wers nicht erkennt, möge ihn sich anhören.
ssynth3:
function RauschenWave(x: Single): Single;
begin
Result := (Random -0.5)*2;
end;
Hausgemachte Ober- und Untertöne
Durch unterschiedliche Wellenformen können wir nun unseren Tönen etwas mehr Fülle verleihen. Es bietet sich jedoch noch eine weitere Möglichkeit an: Obertöne. Statt einer einzelnen Sinuskurve werden hier eine ganze Reihe an Sinuskurven übereinandergelegt. Deren Amplitude ist immer etwas geringer, als die des Haupttones, deren Frequenz jedoch um den Faktor 2^n erhöht:
ssyth4:
Ton := 20 * SinWave(x);
Ton := Ton + 10 * SinWave(x*2); //1 Oktave höher als der Grundton
Ton := Ton + 7 * SinWave(x*4); //2 Oktaven höher als der Grundton
Ton := Ton + 5 * SinWave(x*8); //3 Oktaven höher als der Grundton
...
Ton := 1.0/(20+10+7+5+...)*Ton;
Äquivalent kann man auch Untertöne erzeugen: Statt Oktavschritte nach oben, geht man Oktavschritte mit der Frequenz nach unten (teilen durch 2):
ssyth4:
Ton := 20 * SinWave(x);
Ton := Ton + 10 * SinWave(1/2*x); //1 Oktave niedriger als der Grundton
Ton := Ton + 7 * SinWave(1/4*x); //2 Oktaven niedriger als der Grundton
Ton := Ton + 5 * SinWave(1/8*x); //3 Oktaven niedriger als der Grundton
...
Ton := 1.0/(20+10+7+5+...)*Ton;
Hüllkurven oder Attack, Decay, Sustain, Release Envelopes
Obwohl sich das alles noch sehr langweilig anhört und an sich nicht wesentlich mehr als ohrenbetäubendes quietschen ist, sind wir schon sehr weit fortgeschritten. Eigentlich fehlt uns gar nicht mehr viel, um wohlgeformte Klänge aus den Boxen zu zaubern. Bevor wir das jedoch tun können, benötigen wir noch ein kleines Hilfsmittel: eine Hüllkurve. Das ist an sich nicht mehr, als ein simulierter Lautstärkenverlauf des Anschlages eines Instrumentes, der sich bei vielen Instrumenten in 4 Teilbereiche aufspaltet:
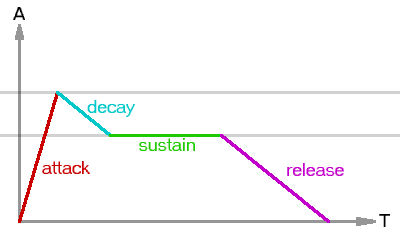
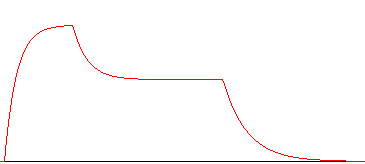
Attack: Der Attack-Teil beschreibt den Lautstärkenverlauf direkt beim und nach dem Anschlag. Die Saite gibt vorerst keinen Ton von sich. Durch Zupfen oder Anschlagen schnellt der von ihr erzeugte Schalldruck in kurzer Zeit auf sein Maximum. Danach fällt die Lautstärke während der Decay-Phase auf einen mittleren Wert zurück, verweilt dann in der Sustainphase eine Zeit lang auf nahezu konstantem Niveau (für uns soll echt konstant genügen), worauf sich die Releasephase anschliesst, in der der Ton - häufig gedämpft - ausklingt:
Prinzip einer ADSR_Hüllkurve:
Zur Lautstärkenregulierung bietet sich die Amplitude unserer Wellenfunktionen an, die wir ganz einfach durch Multiplikation des Sampels mit einem Wert zwischen Null und Eins nach belieben manipulieren können. Daneben müssen wir jedoch beachten, dass unser Gehör auf exponentiell steigende "Werte" geeicht ist, der einfache Kurvenverlauf auf dem obigen Bild würde seltsam klingen. Wandeln wir den Graphen also ein wenig um:
Mithilfe der exp Funktion sollte ein Jeder imstande sein, eine entsprechende Funktion zusammenzustöpseln.
Etwas ADSR-Hüllkurvenquellcode:
function ADSREnvelope(t, a, d, s, r, maxlevel, holdlevel : Single): Single;
const
e = 2.71828182846;
Start = -4.65;
Intervallaenge = 1.0 - Start;
var
Pos, x, delta : Single;
begin
if t < 0 then
begin
Result := 0;
Exit;
end;
//Attack
Pos := a;
if t < Pos then
begin
x := 1.0 - t/a; //x zwischen 0 und 1
x := x * Intervallaenge + Start; //x auf das Intervall mappen
Result := (1.0 - 1/e*(Power(e, x)))*maxlevel;
Exit;
end;
//Decay
Pos := Pos + d;
if t <= Pos then
begin
delta := maxlevel - holdlevel;
if delta <= 0.0 then
begin
Result := holdlevel;
Exit
end;
x := 1.0 - (t - Pos + d)/d;
x := x * Intervallaenge + Start;
Result := Maxlevel - (1.0 - 1/e*(Power(e, x)))*delta;
Exit;
end;
//Sustain
Pos := Pos + s;
if t <= Pos then
begin
Result := holdlevel;
Exit
end;
//Release
Pos := Pos + r;
if t <= Pos then
begin
x := 1.0 - (t - Pos + r)/r;
x := x * Intervallaenge + Start;
Result := holdlevel - holdlevel * (1.0 - 1/e*(Power(e, x)));
Exit;
end;
Result := 0.0;
end;
Zusätzlich benötigen wir noch ein paar weitere Hüllkurven, die ich hier jedoch etwas weniger ausführlich beschreiben werde:
Eine Attack-Sustain-Release-Hüllkurve hat, wie ihr Name verrät 3 Phasen. Im Attack Bereich schwillt die Lautstärke auf ihr Maximum, bleibt dann im Sustain Bereich auf diesem Niveau, um schließlich wieder wie gehabt in der Release-Phase abzufallen.
Eine abbrechbare Attack-Decay-Hüllkurve: Der Attack Bereich ist wie gehabt. In der Decay-Phase fällt die Lautstärke bis auf das Null Niveau ab. Dieser Vorgang kann jedoch an jeder beliebigen Stelle abgebrochen werden und in eine gedämpfte Release-Phase übergehen.
Ein paar synthetische Musikinstrumente
Nun wird es wirklich einmal Zeit, Töne zu erzeugen, bei denen man sich nicht nach kürzester Zeit gequält die Ohren zuhalten muss. Eine gute Möglichkeit dies zu erreichen, besteht darin echte Musikinstrumente zu simulieren. Die einfachen Mittel, die wir bis jetzt kennengelernt haben, reichen dafür völlig aus. Ich werde hier nicht an jeder Stelle Quellcodes mitliefern, ein Blick in die Dateien des synth5 Projektes sollte jedoch Klarheit schaffen. Beim Nachstellen eines Instrumentes ist v.a. ein wenig mit den Parametern spielen angesagt - den Spass will ich euch nicht nehmen. Viele meiner Instrumente sind sicherlich noch verbesserungsfähig.
Klavier
Das Öffnen eines Klavieres kann uns sehr dabei helfen, herauszufinden, wie wir einen Ton synthetisieren müssen. Das typische Klavier besitzt 52 weiße Tasten, die mechanisch die ihnen zugehörigen Saiten mit einem Hammer anschlagen. Zu jeder Taste gehören 3 gespannte, metallische Saiten, die leicht gegeneinander verstimmt sind, so dass eine Schwebung entsteht. Ein Klavier hat einen sehr vollen Ton, so dass wir davon ausgehen können, dass jeder Ton aus einer ganzen Reihe an sinusförmigen Obertönen besteht.
Kommen wir noch zu unserer Hüllkurve: Durch den Anschlag mit dem Hammer steigt die Lautstärke schnell auf ihr Maximum. Bei längerem Tastendruck fällt die Lautstärke langsam ab und wird nach dem loslassen stark gedämpft (Durch Benutzung der unteren Pedale lässt sich hier viel verändern - d.h. hier kann man ruhig ein wenig variieren und herumspielen). Wesentlich an den Hüllkurven ist jedoch, dass die einzelnen Abschnitte der AD-Hüllkurve in ihrer Länge von der Frequenz des Grundtones abhängig sind, weshalb man die Längen nicht in Zeitdauern angibt, sondern durch die Zahl der Schwingungen.
Klavinett
Das Klavinett ist dem Klavier sehr sehr ähnlich. Um seine etwas rauheren Töne zu synthetisieren eignen sich Dreiecke oder Sägezähne sehr gut. Mit Dreiecken klingt das Klavinett ziemlich sanft, mit Sägezähnen dagegen schon sehr hart - was die zweite Variante in Verbindung mit tiefen Tönen sehr imposant erscheinen lässt. An den Hüllkurven des Klaviers muss man dagegen nichts ändern.
Flöte
Wir wollen uns hier mit einer einfachen Flöte begnügen: Man nehme eine ASR-Hüllkurve und eine Dreiecks-Schwingung. Testweise kann man auch einen Sägezahn ausprobieren, der dann zwar nicht mehr nach einer Flöte klingt, jedoch in den tiefen Tönen sehr schöne Ergebnisse liefert. Die Attack und Release Zeiten sollten sich ähneln. Üblicherweise wählt man sie rel. kurz.
Glocken
Glocken geben einen sehr untertonreichen, feinen Klang von sich, entsprechend wählt man als Wellenfunktion den Sinus. Bei vielen Glocken lässt sich auch eine Schwebung heraushören. Als Hüllkurve wählt man wie beim Klavier einen AD-Envelope.
Oktaven, Halbtöne und was sonst dazugehört
Wer sich Synth5 schon ein wenig genauer angeschaut hat, wird festgestellt haben, dass sich dort die Frequenzen für die Töne nicht mehr frei wählen lassen, sondern eine Klaviatur zur Eingabe dient. Wollen wir also ein paar Worte zur Berechnung der Frequenzen, die zu den einzelnen Tasten gehören, verlieren:
Ein Oktavschritt verdoppelt die Frequenz, um also vom Kammerton a auf a' zu kommen, muss 440Hz * 2 gerechnet werden (Kammerton a ist auf 440Hz bzw. 436Hz festgelegt).
Eine Oktave soll dann in 12 Teile zerlegt werden, so dass durch Multiplikation mit einem Faktor der nächst höhere Ton entsteht: Da eine Oktave einer Frequenzverdoppelung entspricht, muss für einen Halbton mit dem Faktor 12te Wurzel aus 2 = 2^(1/12) multipliziert werden.
Abschluss
Wer etwa 14 MB Festplattenplatz frei hat, möge einmal synth_test starten, um Beethovens Für-Elise mit Glocken gespielt zu hören. Wenn Interesse besteht, werde ich den Synthesizer vielleicht auch noch vor dem Projekt veröffentlichen, zu dem er eigentlich gehört: Ein bischen Feedback wäre sicher angebracht.
Ich hoffe eure Ohren haben diesen Angriff meinerseits gut überstanden. Vielleicht konnte ich dieses Thema ja halbwegs entmystifizieren, wo es doch eigentlich eine ganz andere Thematik als die üblichen DGL Tutorials beschreibt. Ich fand es jedenfalls faszinierend, hier in eine auch für mich bis dato völlig unbekannte Welt vorzustossen, wobei das Meiste einfach aus reinem Ausprobieren entstanden ist. Gut, ich muss zugeben, dass ich hin und wieder in ein altes Buch zum Synthesizer löten gespickt habe und auch mein Dad hi und da mit Rat zur Seite stand - tagelanges rumspielen mit Geräuschen, die durchs gesamte Haus hallen können nunmal nicht ungehört bleiben. Jemand, der selbst in seinen jüngeren Jahren einmal einen Synthesizer gebaut hat, lässt es eben nicht kalt, wenn bekannte Geräusche ertönen - wenn auch nicht analog mit Schaltungen, sondern digital erzeugt ;-).
Euer Delphic
|
|
||
Vorhergehendes Tutorial: Tutorial Multithreading |
Nächstes Tutorial: - |
|
|
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen. |
||