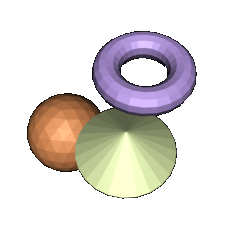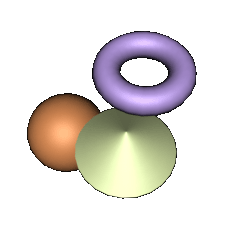Tutorial Lektion 8

Das Wesen von Hell und Dunkel - Licht

Licht an

Hi, und wieder melde ich mich mit einem neuen Tutorial zurück. Heutiges Thema: Licht. Ohne Licht wäre die Umwelt dunkel und kein Pflänzchen könnte Zucker mittels Photosynthese erzeugen. Gäbe es kein Licht, so gäbe es die Welt nicht, wie wir sie kennen. Um in den eigenen OpenGL Programmen eine auch nur annähernd realistische Atmosphäre zu erzeugen ist Licht entsprechend unabdingbar. Man kann Szenen dadurch einen düsteren, geheimnisvollen oder auch einen farbenfrohen, fast kitschigen Stil verleihen.

Arten des Lichts

In OpenGL gibt es unterschiedliche Arten des Lichts. Umgebungs-Licht (Ambient) ist eine Art des Lichts, dessen Richtung nicht zu erkennen ist. Es entsteht durch mehrfache Reflexion an Wänden oder anderen Flächen. Entsprechend gut vertreten ist es in Räumen, aber auch in der freien Natur umgibt uns nicht zu wenig davon. An sich ist es das am schwierigsten zu berechnende, aber in vielen Szenen reicht es aus, eine Konstante vorzugeben - so macht es jedenfalls OpenGL.

"Diffuses" Licht (Diffuse) dagegen lässt die Richtung aus der es kommt erkennen. Je stärker eine Seite in das Licht gehalten wird, desto heller erscheint die Oberfläche. Je weiter man eine Fläche vom Licht abwendet, desto dunkler wird die Oberfläche. Die eintreffenden Lichtstrahlen werden in alle Richtungen verteilt, so dass die Oberfläche von allen Augenpositionen gleich hell erscheint.

Glanz (Specular) kommt aus einer bestimmten Richtung und tendiert dazu, in einer bestimmten Richtung besonders hell zu erscheinen. Plastik, gebürstetes oder nicht matt lackiertes Metall oder auch geschliffene Edelsteine haben einen hohen Glanzanteil, während Holz, Kohle und Wandfarbe so gar nicht glänzen wollen.

Materialeigenschaften

Der vom Licht erzeugte Eindruck hängt aber nicht nur vom Licht selbst ab, sondern auch vom beleuchteten Material. Eine Kohleplatte wirkt im selben Licht anders, als eine polierte Edelstahloberfläche oder das Blech eines lackierten Autos. Deshalb gibt es in OpenGL die sog. Materialeigenschaften. Sie entsprechen denen des Lichts selbst, nur geben sie den Reflexionsgrad und nicht die Intensität wieder.

Hier im Wiki findet ihr in der Materialsammlung eine Auswahl von Parameterwerten.

Objekte können nun aber auch selbst Licht emittieren. Deshalb befindet sich unter den Materialeigenschaften zusätzlich noch ein Emissionswert. Ein Objekt mit Emission ist also auch bei kompletter Dunkelheit noch sichtbar, so z.B. die grüne Leuchtdiode an meinen Boxen, wenn ich die Rollläden geschlossen habe. Schade nur, dass OpenGL dieses emittierte Licht nicht auch auf andere Objekte überträgt :-(.

Normalen

OpenGL berechnet die Farbe des Lichts, das auf ein Objekt trifft mit Hilfe der Richtung aus der das Licht kommt und der Ausrichtung der Oberfläche eines Vertex. Nun stellt sich die Frage: in welche Richtung zeigt denn die Oberfläche? Wir können bei der Übergabe der Vertexdaten einfach mit glNormalx die Normalen angeben. Die Länge des Normalenvektors sollte 1 sein. Bei einer Kugel entspricht die Normale übrigens immer der Richtung des Mittelpunktes zum betrachteten Vertex. Für kompliziertere Gegenstände gibt es weiter unten ein paar Tipps zum Berechnen der Normalen auf "Nachbarschaftsbasis".

Erste Lichtstrahlen

Licht an

Es wird Zeit. Machen wir erste Gehversuche mit OpenGL Licht! Wir brauchen dazu nicht viel zu tun. Mit glEnable(GL_LIGHTING) schalten wir die Lichtberechnung scharf und müssen dann eine Lichtquelle aktivieren. Das geht mit glEnable(GL_LIGHTx) (Zur Information: OpenGL Implementationen müssen 8 Lichter unterstützen. Es gibt aber Implementationen, die hier mehr zu bieten haben. Um Zugriff auf alle vorhandenen Lichter zu erhalten, genügt es zu GL_LIGHT0 einen entsprechenden Wert zu addieren. GL_LIGHT0+8 wäre dann z.B. das 9. Licht).

  glEnable(GL_LIGHTING);
  glEnable(GL_LIGHT0);
  glEnable(GL_COLOR_MATERIAL);

Sonnenbrand erzeugen

Der nächste Schritt besteht darin, die Eigenschaften der Lichtquelle(n) an OpenGL weiterzureichen. Dies läuft immer mit der Funktion glLightx. Sie nimmt 3 Parameter: light: Die Lichtquelle die gerade eingestellt wird. pname: Die Eigenschaft, die wir manipulieren möchten. params: Der neue Wert der Eigenschaft.

Mit pname dürfen wir aus einer ganzen Sammlung von Eigenschaften schöpfen:

Eigenschaft	Standard Wert	Bedeutung
GL_AMBIENT	0.0, 0.0, 0.0, 1.0	Ambienter RGBA Anteil des Lichtes
GL_DIFFUSE	1.0, 1.0, 1.0, 1.0	Diffuser RGBA Anteil des Lichtes
GL_SPECULAR	1.0, 1.0, 1.0, 1.0	Glanz RGBA Anteil des Lichtes
GL_POSITION	0.0, 0.0, 1.0, 0.0	Koordinaten des Lichtes
GL_SPOT_DIRECTION	0.0, 0.0, -1.0	Richtung des Spotlights
GL_SPOT_EXPONENT	0.0	Spotlight-Exponent
GL_SPOT_CUTOFF	180.0	Spotlight Sperrwinkel
GL_xxx_ATTENUATION	...	Abschwächung des Lichtes mit der Entfernung

Materialeigenschaften übergeben

Das gleiche Spielchen müssen wir mit den Materialeigenschaften treiben. Diesmal ist die Funktion glMaterialx der Dreh und Angelpunkt. Die Parameterfolge ist die gleiche wie bei glLightx.

Eigenschaft	Standard Wert	Bedeutung
GL_AMBIENT	0.2, 0.2, 0.2, 1.0	RGBA Reflexionsgrad von ambientem Licht
GL_DIFFUSE	0.8, 0.8, 0.8, 1.0	RGBA Reflexionsgrad von diffusem Licht
GL_SPECULAR	0.0, 0.0, 0.0, 1.0	RGBA Glanzreflexionsgrad des Lichtes
GL_SHININESS	0.0	Glanz-Exponent
GL_EMISSION	0.0, 0.0, 0.0, 1.0	RGBA Emission des Materials
GL_COLOR_INDEXES	0, 1, 1	Ambient, diffuse, specular Farbindices

Beispiellicht

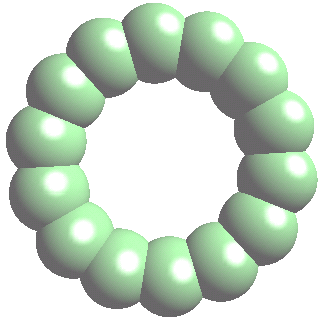
Das Beispiel mit den Kugeln wurde mit folgendem Code erzeugt:

  procedure TStationarySphereState.RenderState;
  const
    mat_specular   : Array[0..3] of GlFloat = (1.0, 1.0, 1.0, 1.0);
    mat_shininess  : Array[0..0] of GlFloat = (50.0);
    mat_ambient    : Array[0..3] of GlFloat = (0.4, 0.4, 0.4, 1.0);
    mat_diffuse    : Array[0..3] of GlFloat = (0.4, 0.8, 0.4, 1.0);

    light_position : Array[0..3] of GlFloat = (10.0, 10.0, 0.0, 1.0);
    light_ambient  : Array[0..3] of GlFloat = (0.8, 0.8, 0.8, 1.0);
    light_diffuse  : Array[0..3] of GlFloat = (0.8, 0.8, 0.8, 1.0);

  begin
    glMaterialfv(GL_FRONT, GL_SPECULAR,  @mat_specular[0]);
    glMaterialfv(GL_FRONT, GL_SHININESS, @mat_shininess[0]);
    glMaterialfv(GL_FRONT, GL_AMBIENT,   @mat_ambient[0]);
    glMaterialfv(GL_FRONT, GL_DIFFUSE,   @mat_diffuse[0]);

    glLightfv(GL_LIGHT0, GL_AMBIENT,  @light_ambient[0]);
    glLightfv(GL_LIGHT0, GL_DIFFUSE,  @light_diffuse[0]);
    glLightfv(GL_LIGHT0, GL_POSITION, @light_position[0]);

    glEnable(GL_COLOR_MATERIAL);
    glEnable(GL_LIGHTING);
    glEnable(GL_LIGHT0);
     ...Szene Rendern...
  end;

Etwas schwächer bitte

Viele Lichtquellen werden mit der Entfernung schwächer. Bei unserer Sonne tritt dieser Effekt so gut wie nicht auf, bei kleinen Funzeln dagegen ist recht bald die maximale Leuchtweite erreicht. Diesen Effekt können wir auch mit OpenGL nachahmen.

Auf diesem Bild ist schön zu erkennen, dass die Kugeln rechts oben heller sind als die links unten, welche weiter von der Lichtquelle entfernt sind (wer nichts sieht, spiele doch mal bitte mit dem Kontrast und der Helligkeit des Monitors - ich kann nicht versprechen, dass der Effekt auf jedem Monitor so schön wie auf meinem herauskommt). Wie wird nun dieser Effekt erzeugt?

OpenGL kennt einen sog. Attenuation Factor:

Attenuation Factor = 1 / (k_c + k_l*d + k_q*d*d)

• d = Entfernung zwischen dem berechneten Vertex und der Lichtquelle
• k_c = GL_CONSTANT_ATTENUATION
• k_l = GL_LINEAR_ATTENUATION
• k_q = GL_QUADRATIC_ATTENUATION

Dieser wird Faktor bei der Lichtberechnung einfach mit den Lichtstärken multipliziert, so dass das Licht stärker oder schwächer wird. Übergeben werden die Werte wieder mittels glLightx:

  glLightf(GL_LIGHT0, GL_CONSTANT_ATTENUATION, 1.0);
  glLightf(GL_LIGHT0, GL_LINEAR_ATTENUATION, 0.001);
  glLightf(GL_LIGHT0, GL_QUADRATIC_ATTENUATION, 0.004);

Das Positionsproblem

Lichter sind unterschiedlich - Manche sind fest an den Kopf des Betrachters gekoppelt, andere irgendwo in der Szene platziert und wieder andere sind unendlich weit entfernt und ihr Licht trifft parallel auf die Gegenstände. All dies will simuliert werden. OpenGL hält es parat. Uns kommt auch noch zugute, dass OpenGL die Übergabe der Licht Position genauso behandelt wie die eines Vertex und entsprechend durch die Modelview Matrix jagt.

Unendlich weit entfernte Lichter

Das Universum, die Milchstraße, der äußere Ring, unser Sonnensystem, die Sonne und unsere Erde. Das Licht, das unsere Sonne ausstrahlt und bei uns auf der Erde ankommt, trifft uns in nahezu parallelen Lichtstrahlen. Damit verhält sich die Sonne wie eine unendlich entfernte Lichtquelle. Wenn wir eine solche Lichtquelle angeben wollen, ist also nicht ihre Position interessant (wobei das auch ginge), sondern allein die Richtung aus der das Licht kommt. Wie? Wir setzen die w-Koordinate(=die letzte Koordinate) der Position auf 0. Unsere unendlich weit entfernte Lichtquelle ist komplett. Sinnigerweise ist dann im übrigens auch Attenuation abgeschaltet.

Stationäre Lichtquellen

Lichtquellen, die an einer bestimmten Stelle in der Szene stehen, müssen mit der Kamerabewegung mitgeschoben werden. Entsprechend wird das Licht angegeben werden, bevor die Modelviewmatrix durch Objekte verschoben wird, aber nachdem die Kamera initialisiert wurde.

  glLoadIdentity;
  //..glRotatef, glTransaltef.. für die Kamera
  glLightfv(GL_LIGHT0, GL_POSITION, @position[0]);
  glPushMatrix;
    //..glRotatef, glTransaltef.. für die Objekte
    DrawObjekts;
  glPopMatrix;

Relatives Licht

Wollen wir stattdessen unsere Lichtquelle relativ zu einem bestimmten Objekt bewegen, so müssen wir ein wenig anders vorgehen: Erst die Modelviewmatrix so bearbeiten, dass wir das Objekt zeichnen könnten, vor dem Zeichen selbst jedoch die Matrixfunktion für das Licht ausführen und die Lichtposition übergeben:

  //..glRotatef, glTransaltef, glMultMatrix, etc...
  glPushMatrix;
    glRotatef(Drehung, 0.0, 1.0, 0.0);
    glLightfv(GL_LIGHT0, GL_POSITION, @position[0]);
  glPopMatrix;
  DrawObject;

Lichtquellen, die an der Kamera kleben

Wenn eine Lichtquelle immer relativ zum Betrachter sein soll(wenn also das Licht z. B. feste am Kopf montiert ist, wie bei einem Minenarbeiter), so langt es die Position des Lichts zu definieren, bevor die Modelviewmatrix mit der Kameraposition und Drehung bearbeitet wurde:

  glLoadIdentity;
  glLightfv(GL_LIGHT0, GL_POSITION, @position[0]);

Spot an!

Wer kennt sie nicht, die Spotlights? Im Fernsehen und Theater oft gebraucht, aber auch im realen Leben, z.B. bei Taschenlampen, Suchscheinwerfern (etwa noch keinen in der Hand gehabt? Ich schon :-) ), etc. oft zu sehen. Leider benötigt man nicht selten eine ganze Schar von ihnen, wozu sich die OpenGL Lichter nur schlecht eignen - aus der Patsche hilft da oft Blending oder andere Techniken. Wenn man mit entsprechenden Projektions-Techniken noch keine Erfahrungen hat, müssen die OpenGL-Lichter dann aber doch wieder herhalten.

Parameter setzen

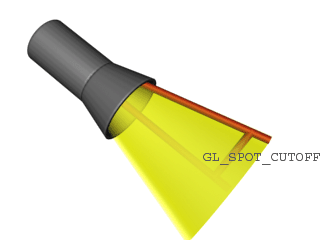
Schauen wir uns die Lichtparameter für Spotlights an: GL_SPOT_DIRECTION gibt die Richtung an, in die das Spotlicht zeigt. Diese lässt sich wieder mit Hilfe geschickter Platzierung im Code durch die Modelviewmatrix jagen um den gewünschten Effekt zu erzielen - wie immer eben. GL_SPOT_CUTOFF gibt den Winkel an, der zwischen Richtung und max. Auswurf besteht. Zuletzt gibt es noch den GL_SPOT_EXPONENT, der beschreibt, wie stark die Lichtstärke nach außen hin abnimmt.

const
    light_position : Array[0..3] of GlFloat = (0.0, 10.0, 0.0, 1.0);
    light0_ambient  : Array[0..3] of GlFloat = (0.8, 0.0, 0.0, 1.0);
    light0_diffuse  : Array[0..3] of GlFloat = (0.8, 0.0, 0.0, 1.0);
  var
    LightDirection : Array[0..2] of GlFloat;
  begin
    LightDirection[0] := Sin(Position)/2;
    LightDirection[1] := -1.0;
    LightDirection[2] := 0.0;
    glLightfv(GL_LIGHT0, GL_SPOT_DIRECTION, @LightDirection[0]);

    glLightf(GL_LIGHT0, GL_SPOT_CUTOFF, 10.0);
    glLightf(GL_LIGHT0, GL_SPOT_EXPONENT, 50.0);

    glLightfv(GL_LIGHT0, GL_AMBIENT,  @light0_ambient[0]);
    glLightfv(GL_LIGHT0, GL_DIFFUSE,  @light0_diffuse[0]);
    glLightfv(GL_LIGHT0, GL_POSITION, @light_position[0]);
    glEnable(GL_LIGHT0);
    glEnable(GL_LIGHTING);
    //...
  end;

Zur besseren Illustration ein Bild

glLightModel?

Bislang haben wir einen Befehl völlig ausser Acht gelassen: glLightModelx. Er nimmt zwei Parameter: pname und param:

Eigenschaft	Standard Wert	Bedeutung
GL_LIGHT_MODEL_AMBIENT	0.2, 0.2, 0.2, 1.0	Abientes RGBA Licht der gesamten Szene
GL_LIGHT_MODEL_LOCAL_VIEWER	0.0 oder GL_FALSE	Lokaler oder unendlicher Viewport. Wirkt bei Specular Reflexionen: GL_FALSE Die Richtung von Betrachter zu Vertex wird nur 1 mal berechnet und bleibt damit für alle Vertices konstant. GL_TRUE Die Richtung Betrachter zu Vertex wird für jedes Vertex neu berechnet, was in einem realistischeren Anblick endet.
GL_LIGHT_MODEL_TWO_SIDE	0.0 oder GL_FALSE	Einseitiges oder doppelseitiges Lighting

Das Vertexproblem

Die Benutzung von Licht muss bislang auf euch sehr einfach gewirkt haben. Aber der eine oder andere wird es vielleicht schon herausgelesen haben: OpenGL Licht wird per Vertex und nicht per Pixel berechnet. Das Problem dabei ist, dass sich mit der Auflösung des Objekts das Aussehen des Lichts stark ändern kann. Bei diffusem und ambientem Licht spielt das kaum eine Rolle. Specular und Spotlights reagieren empfindlich. Die schönen Rundungen, die diese Lichtarten häufig ausbilden, können verschandelt werden. Die Ergebnisse sind nicht mehr wirklich rund, vielmehr eckig und kantig. Ihr glaubt mir nicht? Dann schaut nicht zu genau hin:

Und was lernen wir draus? Schönes Licht braucht viele Vertices.

Normalen die 2.

Länge = 1?

Kommen wir also nun wie versprochen noch einmal zu den Normalen zurück. Normalen, die mit glNormalx angegeben werden, werden, abgesehen von Verschiebungen, wie Vertices mit der Modelview Matrix multipliziert. Normalen sollten für korrekte Lichtberechnung die Länge 1 haben (ist sie länger, so erscheint das Objekt heller, ist sie kürzer, so wird das Objekt dunkler). Ist mit der Multiplikation mit der Modelviewmatrix auch eine Skalierung verbunden, so haben wir ein Problem, denn die Länge ist nicht mehr 1. Um das zu beheben, kann vermittels glEnable(GL_NORMALIZE) OpenGL angewiesen werden, die Normalen selbst auf Länge eins zu skalieren. Aber Achtung: Kostet Rechenleistung.

Einfache Normalen

Manchmal ist die Berechnung von Normalen ganz einfach. So bei Kugeln. Die Richtung die der Mittelpunkt zu irgendeinem Vertex auf der Oberfläche beschreibt, ist gleich der Richtung der Normalen - sie muss nur noch normiert werden. Bei Flächen auf den Achsen muss unsereins auch nicht groß nachdenken, wie denn die passende Normale auszusehen hat. Aber wie ist es, wenn unser betrachteter Körper keine so einfache Oberfläche hat? Was dann?

Normalenberechnung per Dreieck

Will man anhand von Dreiecksdaten Normalen erzeugen, so muss man mal wieder zur Mathematik rüberschauen - die haben das ideale Werkzeug dafür: Das Vektor-Kreuzprodukt. Um die Normale der Fläche beschrieben durch die 3 Ecken V₁, V₂, V₃ zu bekommen, braucht man nur zu rechnen:

N = (V₁ - V₂)x(V₂ - V₃)

Wenn wir das für jedes Polygon durchziehen, dann können wir für jeweils 3 Vertices die Normale angeben. Das schaut ein bisschen eckig aus, bringt uns unserem Ziel aber gewaltig näher. Erinnert irgendwie an die ersten Spiele, die mit Licht arbeiteten... Flatshading war schon was schönes, aber OpenGL kann mehr, wie wir bereits an den Kugeln gesehen haben.

Und nicht vergessen: Die Normalen sollten noch auf die Länge 1 gebracht werden, siehe Normale.

Normalen glätten

Um die Polygone nun ein wenig unsichtbarer zu machen, gibt es ein einfaches Hilfsmittel: Man nehme die direkt anliegenden Flächennormalen um ein Vertex, bilde den Durchschnitt und voilà: Unser Objekt schaut schon runder aus. An einigen Stellen sollte man damit aber vorsichtig walten: Geht es einmal wirklich scharf um eine spitze Kante, so schaut diese Abrundung vermutlich etwas seltsam und abnormal aus. Also: Nicht einfach drauflos abrunden. Da bei komplexeren Objekten jeder vermutlich sowieso einen 3D Modeller verwendet, bei dem man das etwas feinfühlig kontrollieren kann, sollte das kein größeres Problem sein - jeder der seinen eigenen Modeller schreibt, muss sich natürlich etwas einfallen lassen - nützlich erweist sich hier das Skalarprodukt, da man damit den Winkel zwischen zwei Normalen bestimmen kann. Ist der Winkel zu groß, kann es sich nicht um eine Rundung handeln und wir haben es mit einer Kante zu tun - zumindest solange unsere Polygondaten halbwegs fein aufgelöst sind.

Das etwas andere Licht

Mit OpenGL's Standardmethode einen Beleuchtungseffekt zu erzielen, ist natürlich nicht der Weisheit letzter Schluss. Ein anderer Trick drängt sich bei entsprechendem Wissen über die Möglichkeiten geradezu auf: Environment Mapping, oder im folgendem speziell Sphere Mapping. Den entstehenden Effekt kann man mit einer perfekten Spiegelung vergleichen. Das einzige was wir tun müssen, ist OpenGL anzuweisen, die Texturkoordinaten selbst zu berechnen:

    glTexGeni(GL_S, GL_TEXTURE_GEN_MODE, GL_SPHERE_MAP);
    glTexGeni(GL_T, GL_TEXTURE_GEN_MODE, GL_SPHERE_MAP);
    glEnable(GL_TEXTURE_GEN_S);
    glEnable(GL_TEXTURE_GEN_T);

Das wars schon, wir benötigen nur noch eine Sphere Map:

Wenn man das ganze nun noch mit Multitexturing verknüpft, so kann man eine Texturlage für die normale Textur verwenden und die 2. für das Licht. Eine rote Spheremap erzeugt aber rotes Licht, gell... Happy Coding ;-)

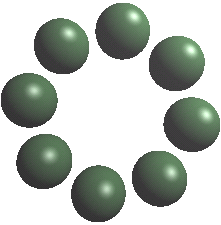
Licht aus

    glDisable(GL_LIGHTING)

Und wieder ist eines meiner Tutorials am Ende. Wenn ich mich nicht irre ists die Nummer 11. Wer gibt mir den verdienten Schnaps aus? Na? Keine Freiwilligen? Schade :-( . In jedem Fall hast Du es jetzt erst einmal hinter Dir und kannst Dich ganz entspannt zurücklehnen - oder, was mir besser gefallen würde: Ein paar OpenGL Programme mit Lichtunterstützung schreiben und uns das Ergebnis als IOTW oder als solches einsenden. Ersatzweise tuts auch etwas freundliches Feedback - das lasst ihr nämlich allesamt immer sehr missen, was das Team zurecht schade findet. Also lasst uns nicht hängen, sondern gebt von euch, was euch an den Tutorials gefällt und was nicht.

und jetzt:

...have a lot of fun!

Delphic & Co-Autor Traude

Vorhergehendes Tutorial: Tutorial Lektion 7	Zur Übersicht	Nächstes Tutorial: Tutorial 2D
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen.