Standardskalarprodukt
Inhaltsverzeichnis
Standard Skalarprodukt
Übersicht
Das euklidische Standardskalarprodukt oder Punktprodukt dient in der 3D Grafik meist zur berechnung von Winkeln, kann jedoch sehr häufig auch eine Reihe anderer zwecke erfüllen.
Definition
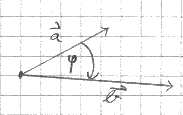
Zwei Vektoren a,b wird eine eindeutige Zahl ‹a,b› das Skalarprodukt zugeordnet:
‹a,b› := ||a||*||b||*cos(Phi) 0≤Phi≤Pi
Haben a,b also die Länge 1, so berechnet das Skalarprodukt ‹a,b› den Cosinus des Zwischenwinkels. Stehen beliebige Vektoren a,b Senkrecht aufeinander, so ist der Winkel gerade Pi/2, der Cosinus also 0 und damit ist das Skalarprodukt gerade dann 0, wenn die beiden Vektoren senkrecht aufeinander stehen. (Beachte: Der Nullvektor ist senkrecht zu allen anderen Vektoren definiert, sogar zu sich selbst.)
Es lässt sich zeigen, daß man das Standard Skalarprodukt sehr leicht berechenn lässt. Seien a=(a1;a2;a3), b=(b1;b2;b3). Dann gilt:
‹a,b› = a1*b1 + a2*b2 + a3*b3
Rechenregeln
- ‹a,a› entspricht der Länge von a im Quadrat, denn ‹a,a› = ||a||*||a||*Cos(0) = ||a||^2
- Linearität in beiden Argumenten:
‹a + b, c› = ‹a,c› + ‹b,c› ‹a, b + c› = ‹a,b› + ‹a,c› ‹lambda * a, b› = lambda * ‹a,b› (Lambda reel) ‹a, lambda * b› = lambda * ‹a,b›
Es ist daher naheliegend das Produkt mit einem Punkt zu shcreiben und die gewohnten Rechenregeln anzuwenden. Deshalb schreibt man häufig auch: a*b := ‹a,b›. Die Regeln werden dann zu:
(a + b).c = a.c + b.c a.(b + c) = a.b + a.c
- Kommutativität: ‹a,b›=‹b,a›
Beispiel
Kugel - Ray - Intersection
Gegeben sei eine Kugel um den Mittelpunkt p mit radius r. Die Bedingung für Punkte x auf der Oberfläche der Kugel ist dann gegeben durch:
||x-p||= r,
d.h. der Abstand von x zu p entspricht dem Radius. Andererseits sei ein Strahl mit Anfang o und richtung d gegeben. Für Punkte x auf dem Strah gilt also:
x = o + t*d (t reel, größer gleich 0)
Um die Schnittpunkte von Kugel und Strahl zu berechnen, wollen wir den Strahl in die Kugel einsetzen:
||x - p|| = r ‹=› ||x - p||^2 = r^2 (Quadrieren) ‹=› ||o + t*d - p||^2 - r^2 = 0 ‹=› ||(o-p) + t*d||^2 - r^2 = 0 (Definiere zur kurzen schreibweise: e := o-p ) ‹=› ‹e + t*d, e + t*d› - r^2 = 0 (||.||^2 als Skalarprodukt) ‹=› ‹e,e› + 2*‹e,t*d› + ‹t*d, t*d› - r^2 = 0 ‹=› ||e||^2 + 2*t*‹e,d› + ||t*d||^2 - r^2 = 0 ‹=› |t|^2*||d||^2 + 2*t*‹e,d› + ||e||^2 - r^2 = 0
Man kann ||d||^2=‹d,d›, ‹e,d› und ||e||^2 - r^2 leicht berechnen und erhät so eine quadratische Gleichung für t, die man mit der Mitternachtsformel schnell löst (Anhand der "Determinante" kann man prüfen, ob überhaupt ein Schnitt vorliegt). Die höchstens 2 Lösungen von t kann man dann in den Strahl einsetzen und bekommt die Schnittpunkte.
Siehe auch