Tutorial Lektion 3: Unterschied zwischen den Versionen
K (→D3D-Verrat) |
(Bild zum Vergleich Translation/Rotation zugefügt) |
||
| Zeile 42: | Zeile 42: | ||
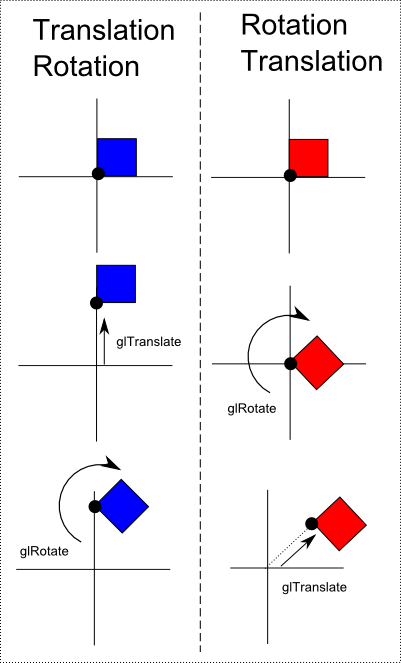
Ein Objekt auf das wir diese Matrix anwenden, wird um 90° um seine Y-Achse gedreht sein. Daraus schließen wir, dass der erste Parameter den Winkel im Gradmaß um den wir rotieren möchten definiert und die 3 folgenden Parameter den Vektor beschreiben um den die Rotation durchgeführt werden soll. Rotationen bergen tatsächlich eine Schwierigkeit, denn es ist nicht immer einfach ein Objekt um die Eigene Achse zu rotieren. Verschiebt Ihr euer Objekt zuerst und beginnt dann die Rotation, so rotiert das Objekt um die eigene Achse. | Ein Objekt auf das wir diese Matrix anwenden, wird um 90° um seine Y-Achse gedreht sein. Daraus schließen wir, dass der erste Parameter den Winkel im Gradmaß um den wir rotieren möchten definiert und die 3 folgenden Parameter den Vektor beschreiben um den die Rotation durchgeführt werden soll. Rotationen bergen tatsächlich eine Schwierigkeit, denn es ist nicht immer einfach ein Objekt um die Eigene Achse zu rotieren. Verschiebt Ihr euer Objekt zuerst und beginnt dann die Rotation, so rotiert das Objekt um die eigene Achse. | ||
| − | Ruft Ihr jedoch zuerst glRotate* und anschließend glTranslate* auf, so unterscheidet sich erzielte Ergebnis von dem vorherigen. | + | Ruft Ihr jedoch zuerst glRotate* und anschließend glTranslate* auf, so unterscheidet sich erzielte Ergebnis von dem vorherigen: |
| + | |||
| + | [[Bild:translation-vs-rotation.png]] | ||
Um diesen Problemen aus dem Weg zu gehen so müsst Ihr Euch vorstellen, dass Ihr den Rotationspunkt im Moment des Aufrufs von glRotate* setzt. Verschiebt Ihr Euer Objekt anschließend so bleibt der Rotationspunkt derselbe und das Objekt beginnt den Rotationspunkt auf einer Bahn zu umkreisen. So gesehen gibt es keinen wirklichen Unterschied und die Rotation um die eigene Achse ist ein Ausnahmefall, denn der Rotationspunkt liegt dann in dem von uns erwarteten Mittelpunkt des Objektes. | Um diesen Problemen aus dem Weg zu gehen so müsst Ihr Euch vorstellen, dass Ihr den Rotationspunkt im Moment des Aufrufs von glRotate* setzt. Verschiebt Ihr Euer Objekt anschließend so bleibt der Rotationspunkt derselbe und das Objekt beginnt den Rotationspunkt auf einer Bahn zu umkreisen. So gesehen gibt es keinen wirklichen Unterschied und die Rotation um die eigene Achse ist ein Ausnahmefall, denn der Rotationspunkt liegt dann in dem von uns erwarteten Mittelpunkt des Objektes. | ||
Version vom 22. Juli 2009, 07:53 Uhr
Inhaltsverzeichnis
Eine Welt des Grauens
Vorwort
Liebe Leser, nachdem Ihr hoffentlich den kleinen Schock des letzten Tutorials alle gut überstanden habt, freue ich mich, Euch hier wieder begrüßen zu können. Wer dachte, dass die letzte Lektion bereits schwer war, der sollte dringend Urlaub nehmen. Seid gewarnt! Bevor ich jetzt richtig loslege, solltet Ihr einigermaßen entspannt sein. Wenn dies einer der Tage ist, an denen Ihr nur noch durch eine Kippe oder die Flasche Coke am Leben gehalten werdet, ordne ich erstmal eine kleine Zwangspause an ;).
Der Stoff der jetzt kommt ist sicherlich nicht gerade die leichteste Lektüre. Wer Mathematik studiert, hat Vorteile, wer einigermaßen logisch denken kann auch. Ein Fachidiot, wie ich, hat nur eine Chance... probieren, testen und lernen :). Und weil ich weiß, wie schwer es eventuell sein kann, werde ich nun einfach mal versuchen, ganz simpel anzufangen und das Ganze mit vielen Bildern so gut wie nur irgend möglich zu illustrieren.
Und wenn Ihr nun Angst habt, dass Ihr das nicht packt, weil ich hier so eine Panik verbreite, dann solltet Ihr mich sehen, wie ich hier verzweifelt vor meinen Tasten hänge und mich frage, wie ich das alles bloß in Worte fassen soll :). Aber was soll es? Ran an den Kram!!! Heulen könnt Ihr anschließend im Forum ;).
Das Grauen hat einen Namen
"Kinofilm" vs. "Bahnhof"
Wer kennt nicht "Matrix" und hätte gedacht, dass es davon nicht nur eine, sondern unendlich viele gibt die so genannten "Matrizen". Vor allem am Anfang werden diese Dinger Euch das Leben erschweren und Ihr werdet leichte Neigungen tief in Euch verspüren, dass am besten Euer ganzes Projekt sich nur im Zentrum Eurer Welt abspielt (und dies ist nicht im wahrsten Sinne des Wortes gemeint).
Wer mit Matrizen umgehen kann, beherrscht das Wichtigste an der 3D-Programmierung. Wer nicht zu den Genies zählt, sollte nicht sofort aufgeben, sondern sich viele Beispiele ansehen und viel mit diesen herumspielen.
Wie auch immer... Ihr solltest wissen, dass es bei jedem Rendervorgang mehrere Matrizen gibt, die ganz drastisch das Aussehen der Szene bestimmen. Es gibt in OpenGL drei Bereiche, in denen Matrizen eingesetzt werden. Die so genannte World- oder Modelviewmatrix, die Texturenmatrix und die Perspektivenmatrix. Die zweifellos wichtigste dieser Matrizen ist die Worldmatrix, da sie die Position Eures "Zeichenstiftes" beschreibt und somit Objekte positioniert. Die Texturenmatrix funktioniert fast genauso wie die Worldmatrix nur definiert sie die Ausrichtung der Texturen. Wir werden später auf sie zurückkommen. Die Perspektivenmatrix definiert wesentliche Eigenschaften des Blickfeldes des Betrachters.
Der Befehl glMatrixMode erlaubt eine Änderung der aktuellen Matrix. Mit Hilfe der Konstanten GL_MODELVIEW, GL_TEXTURE oder GL_PROJECTION kann man die Matrix bestimmen. Die Namen der Konstanten sind soweit hoffentlich selbst erklärend. Von nun an bewirken alle Matrixoperationen wie beispielsweise glLoadIdentity oder glTranslate* eine Veränderung der aktuell gesetzten Matrix.
Die Perspektivenmatrix
Wie bereits erwähnt beschreibt die Perspektivenmatrix das aktuelle Sichtfeld. Zum Setzen der Perspektivenmatrix verwendet man in der Regel Befehle wie glFrustum, gluPerspective, glOrtho oder gluOrtho2D.
gluPerspective lässt den Raum beispielsweise dreidimensional erscheinen, indem sich die Größe von Objekten mit zunehmender Entfernung vom Betrachter verringert. Diese Verringerung ist abhängig von dem im ersten Parameter übergebenen Winkel.
glOrtho hingegen ist phantastisch für ein 2D-Blickfeld geeignet, denn diese Art der Projektion enthält keine Tiefe mehr.
Genauere Informationen zu den einzelnen Funktionen könnt ihr unserem OpenGL-Wiki entnehmen.
Auf eine Sache möchte ich jedoch noch eingehen: Einige dieser Funktionen verlangen die Parameter "znear" und "zfar". Diese Parameter beschreiben die zwei Schnittflächen, die das Blickfeld vor dem Betrachter begrenzen. "znear" definiert die Entfernung der Nearclippingplane vom Betrachter. Alle Objekte, die sich vor dieser Ebene befinden sind nicht sichtbar. "zfar" beschreibt die Entfernung der Farclippingplane vom Betrachter. Alle Objekte, die sich hinter dieser befinden werden weggeschnitten. Wenn also wieder einmal nur die Hälfte Eurer Szene auf dem Bildschirm sichtbar ist, versucht die Schnittflächen entsprechend anzupassen!
Die Worldmatrix
D3D-Verrat
Wenn Ihr ebenfalls zu den D3D-Verrätern gehört (wie z. B. ich *g*), dann solltet Ihr Euch möglichst von eurer Denkweise trennen: Jede Positionierung der Kamera erfolgt über ein Drehen und Bewegen der Szene. Das ist vor allem am Anfang ein wenig gewöhnungsbedürftig ("Die Welt dreht sich! Nicht Du!").
Vielmehr wird jede Manipulation direkt an die Modellmatrix übergeben. Das heißt, wenn Ihr glTranslate* aufruft, so ist diese Manipulation bereits bei Euch in die Modellmatrix eingetragen, alle weiteren Objekte werden mit dieser Matrix transformiert. Wer zweimal glTranslate*(2, 0, 0) aufruft wird feststellen, dass glTranslate* nicht zwei Matrizen zurückliefert, sondern nur eine, die dann auf (4, 0, 0) verweist. Am Anfang solltet Ihr also sehr darauf achten, es wird eine Weile dauern bis Ihr dies fest in Eurem Herzen tragt. Nicht sofort aufgeben :)!
Einfach, Kompakt und Funktional
Neben dem Befehl glTranslate*, den wir im letzten Tutorial lieben gelernt haben, gibt es noch weitere Befehle, die sich auf die einzelnen Matrizen auswirken und auf die ich in dem folgenden Abschnitt eingehen möchte.
Dreh- und Angelpunkt des Geschehens
Zunächst beschäftigen wir uns mit der Rotation. Wir versuchen ein Objekt zu erzeugen, welches um 90° um seine eigene Achse gedreht wurde. Das ist nicht sonderlich schwer:glRotatef(90,0,1,0);
Ein Objekt auf das wir diese Matrix anwenden, wird um 90° um seine Y-Achse gedreht sein. Daraus schließen wir, dass der erste Parameter den Winkel im Gradmaß um den wir rotieren möchten definiert und die 3 folgenden Parameter den Vektor beschreiben um den die Rotation durchgeführt werden soll. Rotationen bergen tatsächlich eine Schwierigkeit, denn es ist nicht immer einfach ein Objekt um die Eigene Achse zu rotieren. Verschiebt Ihr euer Objekt zuerst und beginnt dann die Rotation, so rotiert das Objekt um die eigene Achse.
Ruft Ihr jedoch zuerst glRotate* und anschließend glTranslate* auf, so unterscheidet sich erzielte Ergebnis von dem vorherigen:
Um diesen Problemen aus dem Weg zu gehen so müsst Ihr Euch vorstellen, dass Ihr den Rotationspunkt im Moment des Aufrufs von glRotate* setzt. Verschiebt Ihr Euer Objekt anschließend so bleibt der Rotationspunkt derselbe und das Objekt beginnt den Rotationspunkt auf einer Bahn zu umkreisen. So gesehen gibt es keinen wirklichen Unterschied und die Rotation um die eigene Achse ist ein Ausnahmefall, denn der Rotationspunkt liegt dann in dem von uns erwarteten Mittelpunkt des Objektes.
Eine Frage der Größe
Nun ja... was kann man denn noch alles in einer 3D-Welt machen? Ihr habt gelernt, wie man Objekte bewegt und diese durch Rotationen ausrichten kann. Das ist doch schon eine Menge zum Spielen oder? Nun, bei einer Transformation kann für uns noch eine Sache sehr wichtig werden, nämlich die Möglichkeit, zu bestimmen in welcher Größe ein Objekt dargestellt werden kann.
Sicher würde es Sinn machen ein benötigtes Objekt gleich in der richtigen Größe in die Anwendung zu laden. Manchmal ist es aber von Vorteil, wenn man die Größe eines Objektes ohne großen Aufwand verändern kann oder aber mehrere Objekte desselben Typs mit unterschiedlicher Größe darzustellen.
Eine Größenveränderung ist mit Hilfe des Befehls glScale* möglich.
glScalef(1,1,1);
In diesem Fall würden wir das Objekt so zeichnen, wie wir es auch angegeben haben. Das heißt in seiner Originalgröße. Sicherlich ahnst Du bereits, was die Parameter aussagen... sie stehen für das Verhältnis der einzelnen Seiten nach dem Muster X, Y und Z. Würden wir als ersten Parameter statt einer 1 eine 2 einsetzen, würde unser Objekt in seiner räumlichen Ausdehnung bezogen auf der X-Achse doppelt so groß sein. Würden wir stattdessen 0.5 angeben, wäre es nur noch halb so groß.
In Wirklichkeit bewirkt glScale* jedoch keine Veränderung der Größe sondern eine Verzerrung unseres Koordinatensystems. Daher wirkt jeder Aufruf von glScale* auch auf Befehle wie glTranslate*. Aus Sicht der Matrizen lässt sich dieses Phänomen auch recht leicht erklären. In Wirklichkeit erzeugt jeder Aufruf von glRotate*, glTranslate* oder glScale* eine eigene Matrix, die dann mit der aktuellen Matrix (z.B. der Modelviewmatrix) multipliziert wird. Wurde in der Modelviewmatrix bereits ein glScale* verewigt, so wirkt sich dieses bei der Multiplikation der Matrizen auf die Transformationsmatrix aus.
Ich denke ich muss nicht näher darauf eingehen, dass es keine gute Idee ist das Koordinatensystem mit einem Aufruf von glScalef(0, 0, 0) zu zerstören. Was würde es auch für einen Sinn ergeben, das Koordinatensystem in einem Punkt unterzubringen?
Hinweis: Es ist bereits gefährlich nur eine Achse auf 0 zu skalieren, denn dadurch wird die aktuelle Matrix beschädigt (singulär) und Befehle wie gluProject und gluUnProject funktionieren nicht mehr.
Ich hoffe ich habe Euch nun nicht den letzten Funken Hoffnung OpenGL zu verstehen geraubt. Ich kann Euch versichern, dass dieses Verständnis mit der Zeit heranreifen wird.
glScale* ist aber aufgrund seiner phantastischen Eigenschaften nicht nur in der Lage die Größe von Objekten zu verändern sondern es ist auch möglich Objekte zu spiegeln indem man negative Werte an glScale* übergibt. Somit kann sich z. B. ein D3D-Umsteiger das leben vereinfachen indem er mit einem Aufruf von glScalef(1, 1, -1) sicherstellt, dass die Z-Achse in den Bildschirm hinein positiv verläuft.
Jeder, der die Funktion der Modelviewmatrix begreifen möchte, dem möchte ich das Programm Matrixcontrol von Lithander (siehe Anhang) ans Herz legen. Es erlaubt Euch bestimmte Änderungen an der Matrix direkt nachzuvollziehen und wenn man mit dem Programm ein wenig umherspielt wird selbst dem letzten ziemlich schnell ein Licht aufgehen. Wenn nicht, dann hilft nur fleißiges Programmieren und Anwenden und irgendwann klatscht es dann laut, wenn die eigene Handfläche auf der Stirn zum stehen kommt ;).
Virtuelle Gedächtnisse
Vom Pushen und Poppen
Wer diesen Titel ließt und sich nun zwangsläufig daran erinnert, was er bereits alles in seinem Leben konsumiert hat oder neben wem er am nächsten Morgen aufgewacht ist, sei entwarnt! Wir reden hier von etwas ganz anderem...
Wie wir bereits gelernt haben, verändert jeder Aufruf von glTranslate*, glRotate* oder glScale* die Worldmatrix und wirkt sich unmittelbar auf andere Objekte aus. Dies kann durchaus sehr erwünscht sein. Wenn wir allerdings in einer großen Welt verschiedene Objekte positionieren, kann dies schnell zum Fluch werden. Natürlich können wir dem entgegenwirken und zum Beispiel jedes Mal glLoadIdentity aufrufen. Dies hat jedoch den Nachteil, dass die World- Matrix dann eben wieder leer ist und wir z.B. die Camera erst wieder setzen müssen, damit die Objekte an die richtige Stelle transformiert werden.
Eine weitaus elegantere Lösung ist die Verwendung des "Matrixstacks"! Jeder Aufruf von glPushMatrix bewirkt, dass die momentane Matrix auf den Stack geschrieben wird. Alle Manipulationen, die wir dann durchführen, werden wie gewohnt vollzogen. Ist alles gezeichnet, rufen wir mit glPopMatrix, die letzte Matrix vom Stack wieder herunter und haben im Prinzip den letzten Zustand vor unseren Veränderungen rekonstruiert und können dann wieder anfangen, auf dieser Matrix aufzubauen. Natürlich lassen sich auch mehre Matrizen auf den Stack pushen! Dies kann reichlich Zeit sparen, wenn man bedenkt, dass man ansonsten andauernd die Matrix der Szene neu setzen muss.
Um das ganze etwas anschaulicher zu machen, verwenden wir ein einfaches Beispiel. Wir werden zwei Dreiecke jeweils rechts und links vom Ursprung zeichnen. Nachdem wir das linke Objekt gezeichnet haben, werden wir nicht glLoadIdentity einsetzen oder das zweite Objekt entsprechend nach rechts transformieren, sondern eben den Matrixstack zu Hilfe nehmen.
glLoadIdentity();
glTranslatef(0,0,-10);
glPushMatrix();
glTranslatef(-2,0,0);
glBegin(GL_TRIANGLES);
glColor3f(1,0,0); glVertex3f(-1,-1, 0);
glColor3f(0,0,1); glVertex3f( 1,-1, 0);
glColor3f(0,1,0); glVertex3f( 0, 1, 0);
glEnd();
glPopMatrix();
glTranslatef(2,0,0);
glBegin(GL_TRIANGLES);
glColor3f(1,0,0); glVertex3f(-1,-1, 0);
glColor3f(0,0,1); glVertex3f( 1,-1, 0);
glColor3f(0,1,0); glVertex3f( 0, 1, 0);
glEnd();
Wie Ihr seht, setzen wir am Anfang praktisch die Distanz zum Objekt, speichern die Matrix und zeichnen das erste Objekt. Wir setzen dann die Matrix wieder zurück, so dass sie nur noch den Aufruf von glTranslatef(0, 0, -10) beschreibt und transformieren das zweite Objekt... fertig. Man kann auch ohne diese Matrixstacks leben sie können einem aber das Leben auch sehr erleichtern.
I wanna all!
Wer glaubt, dass es das bereits war der irrt. Es gibt noch weitere Möglichkeiten auf die Matrix Einfluss zu nehmen. Der Befehl glLoadMatrix* erlaubt es eine beliebige 4x4 Matrix zu laden und die aktuelle Matrix durch die geladene komplett zu ersetzen.
Der Befehl glMultMatrix* multipliziert die übergebene 4x4-Matrix mit der aktuellen Matrix. Mit diesem Befehl könnte man beispielsweise eigene glScale*- und glRotate*-Befehle schreiben, obgleich sich auch hier über den Sinn streiten lässt. Eine sinnvollere Anwendungsmöglichkeit wird in einem späteren Tutorial vorgestellt werden.
Der Befehl glGet* mit den Tokens GL_MODELVIEW_MATRIX, GL_TEXTURE_MATRIX und GL_PROJECTION_MATRIX ermöglicht euch die einzelnen Matrizen anzufordern.
Weltenformeln
Hier kommt die Sonne...
Genug der Theorie! Es wird langsam Zeit für etwas Praxis...
Nun, um ehrlich zu sein, habe ich an der folgenden Idee ein wenig Zeit benötigt, um ein einigermaßen gut anschauliches Beispiel zu finden... ich will hier nicht weiter darauf eingehen, was ich gerade gehört habe, als mir die Sonne aufging :-D.
Wie auch immer, man kann komplexere Matrixtransformationen sehr leicht mit unseren Sonnensystem beschreiben (Hey, wenn jetzt jemand denkt, dass ich spinne...). Um das Ganze etwas übersichtlicher zu gestalten, werden wir unser Prinzip auf Sonne, Mond und Erde beschränken.
Wie funktioniert unser Sonnensystem? (Warnung, der Autor betritt mal wieder seine ausgeprägte Fantasywelt! [Anm. d. Lektors: Die richtige Sprache dafür hat er ja schon]).
Die Sonne steht im Mittelpunkt und sollte sich in unserem Beispiel nicht selbst bewegen. Sie ist einfach nur im Mittelpunkt und vegetiert dort vor sich hin! Nun gibt es einen kleinen blauen Planeten, namens Erde (wieso er im Sample ein Dreieck ist, sei Eurer Kreativität überlassen...), der zum einen um seine eigene Achse rotiert, viel wichtiger jedoch, sich auch noch um die Sonne dreht. Nun werden sich vor allem die Neulinge unter Euch sadistisch freuen, das Fenster schließen, ihr Delphi starten und drauf los proggen! Das ist doch alles kein Ding, der gerade mal frisch aufgeschnappte Sinus-Satz lässt sich prima mit einbringen! Und schon berechnet man mit Hilfe von Sinus, die Position auf der Kreisbahn und positioniert den Planeten mit glTranslate* an seine Position. Und oh Wunder es klappt. HALT! Wer es nicht gemerkt hat, da war ne Portion Ironie dabei. Bitte Weiterlesen ^__^!
Denn spätestens wenn wir folgende Ergänzung zum Besten geben, werden die ersten Augen wässrig werden, weil die meisten Hirne einem Informationskoller unterliegen. Meines stieg ja schon beim einfachen Sinus aus :-D. Ab und an kann man nämlich nachts weißgräuliche Flecken am Himmel beobachten! Wer annimmt, dass es sich hierbei um eine geschickt platzierte, in Echtzeit berechnete, Textur handelt, ist schief gewickelt! Es handelt sich dabei nämlich um ein Decal, namens Mond. Oha... so schlimm war es schon lange nicht mehr. Dieser bewegt sich in unserem Beispiel auch nicht entlang der Erdachse, sondern auf einer schiefen Bahn, damit man auf der unteren Hemissphäre den Mond auch am Tage noch sehen kann ^___^ (*selbstgefälliges, göttliches Grinsen*). Dies lässt sich nur sehr schwer mit Sinus beschreiben. Bevor wir uns nun jedoch mit einem Block bewaffnen oder den nächsten Mathematik-Professor entführen, damit er die Mathematik für uns übernimmt, greifen wir lieber zu den Sternen und nehmen ein einfacheres Verfahren! Les Matrices!
Und es dreht sich doch!
Die Vorgehensweise ist eigentlich relativ simpel. Wir Zeichnen unsere Sonne im Mittelpunkt unseres Universums. Mit dem Aufruf von glRotate* setzen wir den Rotationspunkt an die Position unseres "Zeichenstiftes". In unserem Fall ist das noch immer die Position der Sonne.
Nun verschieben wir die Erde nach links und die erste Hürde ist genommen. Jetzt müssen wir nur noch den Mond setzen und das funktioniert genauso einfach wie zuvor mit der Erde.
Unser Zeichenstift befindet sich nun an der Position der Erde und daher rufen wir glRotate* auf. Nun müssen wir den Zeichenstift nur noch ein kleines Stück neben der Erde positionieren und den Mond zeichnen. Voila! Es ist vollbracht!
Wenn man genauer darüber nachdenkt erkennt man sehr schnell wie elegant man dieses verhältnismäßig komplizierte Problem gelöst hat.
Wer nun auf Wolke Sieben schwebt und glaubt er könnte sich nun an den nächsten DOOMTitel werfen, der sollte das Programm zuvor noch so erweitern, dass die Sonne, die Erde und auch der Mond sich zusätzlich um die eigene Achse drehen.
Timebased Movement
Wer bereits versucht hat eines der ersten selbst geschriebenen OpenGL-Programme voller Stolz seinem Kumpel vorzuführen wird festgestellt haben, dass die Bewegungen auf dem anderen Rechner schneller oder langsamer abgelaufen sind als es auf dem eigenen Rechner der Fall war.
Dieses Phänomen lässt sich sehr einfach erklären. Nehmen wir an wir bewegen ein Dreieck von links nach rechts um den Wert 1 über den Bildschirm. Eine alte Krücke wie mein PC schafft vielleicht 50 FPS. Das bedeutet das Objekt wird in einer Sekunde genau 50mal um eine Einheit nach rechts verschoben. Das bedeutet insgesamt also um 50 Einheiten in einer Sekunde. Wenn das Programm nun aber auf einem High-End-System läuft werden wir die Szene... sagen wir... 500mal aktualisieren können. Folglich bewegt sich auf diesem Rechner das Dreieck in einer Sekunde um 500 Einheiten.
Das einzige was wir von unserem Dreieck erhaschen können ist ein blitzartiges Zucken auf dem Bildschirm, welches wir schnell als optische Täuschung abtun würden. Wie kann man diesem Problem nun aber entgegen wirken?
Nehmen wir an wir kennen die Zeit, die wir zum Zeichnen eines Frames benötigen und ermitteln anhand dieses Wertes einen Zeitfaktor, den wir in die Bewegung mit einfließen lassen.
NewPosition := OldPosition + Movement * TimeFactor;
Handelt es sich um einen schnellen Rechner so ist der Zeitfaktor entsprechend niedrig und die Bewegung pro Frame verringert sich. Ist der Rechner hingegen langsam so besitzen wir einen hohen Zeitfaktor. Folglich legt das Dreieck auf dem schnelleren Rechner pro Frame weniger Weg zurück als auf dem langsamen. Insgesamt jedoch legen die beiden Dreiecke im gleichen Zeitabstand (z. B. in einer Sekunde) denselben Weg zurück.
Um den Zeitfaktor zu ermitteln muss man lediglich die Zeit für einen Schleifendurchlauf ermitteln. Um eine möglichst hohe Genauigkeit zu erhalten sollte man die Zeit für den letzten Schleifendurchlauf ermitteln und im aktuellen Schleifendurchlauf verwenden.
Nachwort
Wow... und wieder ein wenig Zeit zum Ausspannen und ein paar persönlichen Worten. Ich kann getrost nur eines sagen: Wenn Ihr nun denkt "das war alles ja sehr leicht" habt Ihr irgendetwas falsch gemacht und solltet das Tutorial noch einmal von Vorn durcharbeiten ;). Wenn Ihr jedoch leichte Kopfschmerzen verspürt (ob es nun die Matrizen sind oder der fiese Elementarbereich *sg*...) so habt Ihr alles richtig gemacht ;).
Matrizen sind vor allem vielen Einsteigern sehr fremd. "Übung macht den Meister". Versucht Euch doch einfach mal die eine oder andere Aufgabe selbst zu stellen oder unser "Sonnensystem" selbst einmal nachzuschreiben. Wenn Ihr glaubt, dass das Ganze ganz nett geworden ist, dann schickt es mir doch einfach mal zu. Ich freue mich immer darüber zu sehen, was für Früchte meine Tutorials tragen. *lach* Und wenn sich plötzlich alles um die Erde dreht, dann habe ich a) das Gefühl, dass die Kenntnisse über das Sonnensystem nicht mehr ganz up to date sind oder b) ich einen ziemlich fatalen Fehler beim Erklären gemacht habe :->.
Schreckt auch bitte nicht davor zurück, eine Frage diesbezüglich im Forum zu stellen. Es ist keine Schande, mit einer Matrix Probleme zu haben und vor allem die Erfahrenen unter uns, sollten nur zu gut wissen, was alles die Ursache dafür sein kann, wenn man plötzlich gar nichts mehr auf dem Screen sieht :).
Das Tutorial Matrix2 behandelt das Thema Matrizen, und vor allem wie man Sachen in OpenGL positioniert, noch genauer.
Wir selbst werden uns in den folgenden Kapiteln noch etwas intensiver mit den Matrizen beschäftigen und unter anderem die eine oder andere interessante Spielerei zeigen!
Euer
Phobeus
Dateien
- Der aktuellste Beispiel-Quelltext befindet sich im DGLSDK 2006.1 für Windows
 und Linux
und Linux 
- Alter Delphi-API-Quelltext zum Tutorial

- Alter Delphi-VCL-Quelltext zum Tutorial

- Windows-Binary zum Tutorial

- Pixelpracht - Hier könnt Ihr das Programm "Matrix Control" finden
- Matrix Control
|
|
||
Vorhergehendes Tutorial: Tutorial Lektion 2 |
Nächstes Tutorial: Tutorial Lektion 4 |
|
|
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen. |
||