Aktuelle Version vom 30. Juni 2008, 16:39 Uhr

Hüllkörper (bounding volumes)

Allgemeine Merkmale

Definition und Typen

Wie der Name andeutet, hüllen diese Körper irgendetwas ein, z.B. dreidimensionale Objekte. Hüllkörper werden nicht sichtbar gemacht, sondern sind Hilfskonstruktionen, um Rechenvorgänge zu vereinfachen und zu beschleunigen. Oft lassen sich Berechnungen überhaupt erst mit Hilfe von Hüllkörpern realisieren.

Wesentliches Merkmal aller Hüllkörper: Sie reduzieren komplexe Objeke, die aus einer Vielzahl von Polygonen bestehen können, auf elementare, geometrische Körper. Dabei spielt zunächst die Form der zu umhüllenden Objekte eine Rolle:

Die wichtigsten Hüllkörperformen:

• Kugel (bounding sphere)
• Zylinder (bounding cylinder)
• Quader (bounding box)
• Kegel (bounding cone) - im Vergleich zu den anderen seltener benutzt

Welcher Hüllkörper am besten geeignet ist und wie groß er sein muss, hängt aber auch davon ab, was er im Anwendungsfall leisten soll. In einigen Fällen tritt der Hüllkörper an Stelle des eingeschlossenen Objekts. Er ist quasi ein Ersatzkörper, und die Berechnungen werden mit dem Hüllkörper anstatt mit dem Originalobjekt durchgeführt. Dann ist es wichtig, dass der Hüllkörper möglichst genau "passt". - In anderen Fällen wiederum hat er die Funktion eines Containers. Mit ihm werden pauschale Berechnungen durchgeführt, die für alle eingeschlossenen Polygone gelten. Meistens handelt es sich darum, den gesamten Inhalt des Hüllkörpers von einem Vorgang auszuschließen oder für eine weitere Behandlung zuzulassen. Die Anpassung von Form und Größe spielt hierbei eine untergeordnete Rolle; entscheidend ist vor allem, dass alle Polygone restlos erfasst werden.

Es sollte immer daran gedacht werden, dass nur möglichst einfache und "handliche" Hüllkörper ihren Zweck erfüllen können. Konvexe Polyeder, um ein Beispiel zu nennen, mögen zwar ein Objekt sehr passgenau umschließen, aber der aufwändige Umgang mit solchen Gebilden kann den erstrebten Gewinn an Performance und Einfachheit wieder in Frage stellen.

Komplexe Hüllkörper

Hüllkörper sind keineswegs auf einzelne Objekte beschränkt. So lassen sich ohne weiteres mehrere Objekte oder ganze Bereiche der Szenerie in Hüllkörper packen. Ebenso ist denkbar, mehrere Hüllkörper erneut in einem Hüllkörper zu bündeln. Durch eine solche Gruppierung kann u.U. eine effektive Hierarchie aufgebaut werden:

Hüllkörpergruppe -> einzelner Hüllkörper -> einzelnes Polygon

Die Szenerie muss sich jedoch dafür eignen. Die Hüllkörpergruppen sollten sinnvolle Einheiten darstellen und räumlich nicht zu groß ausfallen.

Der umgekehrte Weg wird bei Hüllkörpern eingeschlagen, die kein ganzes Objekt einschließen, sondern nur einen Teil davon. Um das Objekt vollständig einzuhüllen, sind dann mehrere Hüllkörper erforderlich. So könnte z.B. der Stamm eines Baumes in einen Zylinder, die Krone in eine Kugel gepackt werden. Auf diese Weise erreicht man mit einfachen Körperformen eine gute Passgenauigkeit und kann außerdem differenziert mit verschiedenen Teilen des Objektes umgehen, etwa bei Kollisionen.

Ausrichtung (Orientierung)

Abgesehen von der Kugel lassen sich Hüllkörper auf verschiedene Weise ausrichten:

1. Ausrichtung an den Achsen des Welt-Koordinatensystem
2. freie Ausrichtung, die sich in der Regel nach dem Objekt richtet

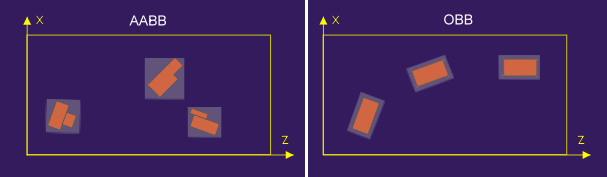
Diese Unterscheidung wird vor allem bei quaderförmigen Hüllkörpern getroffen und hat zu den Begriffen AABB (axis aligned bounding box) und OBB (orientated bounding box) geführt.

Die OBB lässt sich natürlich flexibler einsetzen und bietet mehr Möglichkeiten, erfordert andererseits aber einen größeren Rechenaufwand als die AABB. Während die AABB fast ausschließlich als Container für statische Szenerieobjekte eingesetzt wird, dient die OBB vor allem als Ersatzkörper für statische und bewegliche Objekte.

Zweidimensional: Hüllflächen

Nicht immer sind dreidimensionale Hüllformen erforderlich. Bei flächig angelegten Szenerien, wo sich das meiste in Bodennähe abspielt, können für Selektionszwecke (siehe Anwendung) auch zweidimensionale Formen wie Kreise oder Rechtecke eingesetzt werden. Der Performancegewinn gegenüber "echten" Hüllkörpern ist zwar nicht gravierend, aber Flächen lassen sich einfacher und besser an das Objekt anpassen, da die Höhe nicht berücksichtigt werden muss.

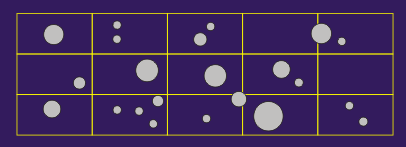
Wenn es um die Raumunterteilung ausgedehnter Szenerien geht, bieten sich ebenfalls oft zweidimensionale Methoden an. Die Objekte werden z.B. in Hüllkreise gepackt, und das Gelände wird - falls sinnvoll oder erforderlich - in ein Netz von Arealen zerlegt.

Sollen für die Raumunterteilung baumartige Strukturen verwendet werden, reicht bei zweidimensionalem Vorgehen ein Quadtree, im Gegensatz zum dreidimensionalen Octree. - Nicht geeignet sind zweidimensionale Hüllformen für Culling-Verfahren (siehe Anwendung); diese sind grundsätzlich dreidimensional angelegt.

Anwendung

Anwendung bei Culling-Verfahren

Bei den Culling-Verfahren geht es darum, alle Objekte, die nicht im Sichtbarkeitsbereich liegen, vom Zeichnen auszuschließen. Die Frage ist nicht, ob und in welchem Umfang die Objekte wirklich auf den Bildschirm gelangen; diese Entscheidung trifft OpenGL anhand der Projektionsmatrix und des Tiefenpuffers. Zweck des Cullings ist vielmehr, die nicht in Frage kommenden Objekte oder Objektgruppen erst gar nicht an OpenGL zu schicken und damit die Render-Pipeline zu entlasten.

Am häufigsten wird wohl das Frustum-Culling (view frustum culling) eingesetzt. Das View-Frustum begrenzt mit 6 Ebenen den Sichtbarkeitsraum in Form eines Pyramidenstumpfes. Die Ebenen (left, right, top, bottom, near und far) müssen unter Berücksichtigung der eingestellten Perspektive bei jeder Ă„nderung der Kameraposition (view point) oder der Blickrichtung (view orientation) neu berechnet werden. Die Normalen der Ebenen sollten zweckmäßigerweise alle nach innen gerichtet sein, damit die Position des Hüllkörpers zu den Ebenen einheitlich berechnet werden kann. Die Frustum-Abfrage liefert 3 mögliche Ergebnisse:

1. Der Hüllkörper und damit das ganze Objekt liegt außerhalb des Frustums. In diesem Fall kann das Objekt ignoriert werden.
2. Der Hüllkörper und damit das ganze Objekt liegt innerhalb des Frustums. Das Objekt ist vollständig sichtbar und wird zum Zeichnen an OpenGL geschickt.
3. Der Hüllkörper schneidet eine oder mehrere Ebenen des Frustums. Das Objekt liegt damit im Grenzbereich des sichtbaren Raums.

Im Fall 3 müsste nun konsequenterweise eine Clipping-Prozedur folgen, indem jedes einzelne Polygon des eingehüllten Objektes auf seine Position geprüft wird. Der Aufwand dürfte aber nur bei ausgedehnten Objekten, die in Relation zum View-Frustum groß sind, gerechtfertigt sein. Kleinere Objekte belässt man am besten im Hüllkörper und ordnet sie den Fällen 1 oder 2 zu. Beim Schneiden der hinteren Frustum-Ebene (far plane) kann z.B. auf das Zeichnen verzichtet werden, wenn der Bereich in Nebel gehüllt ist. Objekte bzw. Hüllkörper, die die rechte oder linke Ebene schneiden, sollten immer gezeichnet werden, sonst kommt es bei Richtungsänderungen zu einem plötzlichen "Aufploppen", wenn das Objekt erstmals vollständig sichtbar wird. Sie gleiten dann nicht ins Bild hinein. - In diesem Zusammenhang ist schließlich zu überlegen, ob die beiden Ebenen top und bottom überhaupt gebraucht werden. Wenn die Kamera nur geringfügig nach oben oder unten geschwenkt wird, ist kaum zu erwarten, dass ein Objekt in Bereiche oberhalb und unterhalb des Frustums gerät.

Weniger geläufig als das Frustum-Culling ist das Occlusion-Culling. Auch hierbei geht es um die Sichtbarkeit von Objekten, diesmal um die Frage, ob ein Objekt von anderen Bestandteilen der Szenerie verdeckt wird (occlusion = Verdeckung). Es liegt nahe, dass die Kameraposition eine erhebliche Rolle spielt; somit könnte das Verfahren z.B. dann interessant werden, wenn sich die Kamera oft in Straßenschluchten oder Innenräumen bewegt.

Zwar lässt sich das Occlusion-Culling mit externen Algorithmen bewerkstelligen, doch diese sind ziemlich aufwändig. Einfacher und effektiver ist es, auf die Unterstützung von OpenGL zurückzugreifen (ab Version 1.5 ???). Das liegt schon deshalb nahe, weil OpenGL intern bereits auf die erforderlichen Informationen, die im Tiefenpuffer liegen, zurückgreifen kann. Die Occlusion-Abfrage erfolgt innerhalb der Klammer glBeginQuery und glEndQuery und hat Ähnlichkeit mit dem Zeichnen von Polygonen, nur dass in diesem Fall lediglich die Sichtbarkeit bzw. Verdeckung festgestellt wird. Das Ergebnis kann mit glGetQueryObject" abgefragt werden. Im Falle einer vollständigen Verdeckung ist das Ergebnis 0.

Ohne die Verwendung von Hüllkörpern ist das Occlusion-Culling nicht sinnvoll. Jedes einzelne Polygon einer Occlusion-Abfrage auszusetzen, würde keinen Performancegewinn bringen, sondern allenfalls eine zusätzliche Belastung zur Folge haben.

Bei den Culling-Verfahren hat der Hüllkörpers die Funktion eines Containers. Er muss demnach so bemessen sein, dass er mit Sicherheit alle Bestandteile des Objektes einschließt. Im Zweifelsfall sollte der Hüllkörper eher zu groß als zu klein bemessen sein.

Anwendung bei der Kollisionserkennung

Bei der Kollisionserkennung (zum Teil auch bei der Kollisionsverarbeitung) kommen beide Grundfunktionen der Hüllkörper zum Tragen. Da die Objekte, die miteinander kollidieren können, in vielen Fällen zu komplex sind, um die erforderlichen Berechnungen mit vertretbarem Aufwand durchzuführen, werden sie durch einfachere Formen ersetzt. Der entstehende Hüllkörper, der hier als Ersatzkörper in Erscheinung tritt, kann sowohl feste als auch bewegte Objekte ersetzen.

Die sechseckige Säule (statisch, links im Bild) wird durch eine Reihe von Dreiecken oder Rechtecken gebildet, doch die Kollision erfolgt wie an einem wirklich runden Zylinder. Wichtig ist, dass das Objekt möglichst exakt eingehüllt wird, und zwar funktionsgerecht. Der Quader, der das Auto einschließt (bewegte OBB, rechts im Bild), muss an den Stellen genau passen, wo Berührungen mit anderen Teilen der Szenerie zu erwarten sind, also etwa in Höhe der Stoßstangen. Hervorstehende Teile (z.B. die Rückspiegel) werden meistens ignoriert und können aus dem Hüllkörper herausragen, sofern sie für eine Kollision nicht in Frage kommen.

Als Container treten Hüllkörper in Erscheinung, wenn bei der Kollisionserkennung eine Vorauswahl getroffen werden soll. Um nicht die Polygone aller Objekte in jedem Frame auf eine mögliche Kollision überprüfen zu müssen, werden zunächst lediglich die Hüllkörper herangezogen. Nur wenn ein Hüllkörper aufgrund seiner Lage bzw. der Geschwindigkeit und Richtung des bewegten Objektes "getroffen" werden kann, erfolgt eine Kollisionsberechnung mit den einzelnen Polygonen. Der Zweck besteht darin, alle nicht in Frage kommenden Objekte möglichst früh und zeitsparend auszuschließen.

Bei der Vorselektion werden vorzugsweise Kugeln und - wenn ein zweidimensionales Verfahren ausreicht - Kreise eingesetzt. Die Hüllkörper bzw. -flächen sollten hinreichend groß sein, im Zweifelsfall eher zu groß als zu klein.

Es gibt zwei Wege, um die Kollision mit Hüllkörpern festzustellen. Für eine exakte Erkennung, die zudem unabhängig von der Geschwindigkeit des bewegten Objektes ist, wird eine Intersektions-Funktion herangezogen. Falls der Bewegungsablauf dagegen aus sehr kleinen Schritten besteht, reicht meistens ein einfacher und schneller Abstandstest.

Sonstiges

Parameter des Hüllkörpers

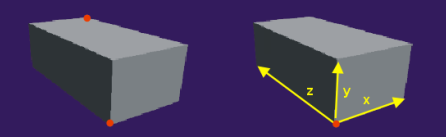
Welche Parameter erforderlich sind, um einen Hüllkörper eindeutig zu beschreiben, richtet sich nach der Art des Körpers. So sind bei der Kugel lediglich der Mittelpunkt und der Radius notwendig. Beim achsenorientierten Hüllquader (AABB) gibt es mehrere Möglichkeiten. Die eine besteht darin, einen Eckpunkt als Positionspunkt festzulegen und zusätzlich die drei Ausdehnungen anzugeben. Diese wiederum könnten zu einem Formvektor zusammengefasst werden. Stattdessen ist es möglich, zwei diametral entgegengesetzte Punkte zu definieren. Die Datenmenge ist in beiden Fällen gleich.

Bei der OBB ist die Siutation anders. Als Bezugspunkt (Positionspunkt) ist ein Eckpunkt in der Regel ungeeignet, weil das Objekt wohl kaum um diesen Punkt rotiert wird. Der Rotationspunkt liegt zweckmäßigerweise etwa in der Mitte der Grundfläche und sollte dann auch zur Positionierung des Hüllkörpers herangezogen werden. Zur Beschreibung von Größe und Form bietet sich wieder der Formvektor an. Hinzu kommt aber noch die Ausrichtung, wobei wiederum unterschieden werden sollte, ob das Objekt seine Richtung ständig ändert oder ob es starr angeordnet ist.

Im ersteren Fall kann die Ausrichtung entweder durch einen Richtungsvektor oder durch zwei Winkel (head und pitch) festgelegt werden. Damit sind zwei Freiheitsgrade genutzt. Ob der dritte Freiheitsgrad, nämlich die Drehung um die nicht richtungsbestimmende Eigenachse, erforderlich ist, hängt von der Anwendung ab. Evtl. muss für die vollständige Ausrichtung noch ein Up-Vektor hinzukommen, es kann aber auch sein, dass die Normale des Untergrundes die Funktion des Up-Vektors übernimmt. *)

Wenn dagegen die OBBs als Ersatzkörper für unbewegte Objekte dienen sollen, z.B. in Kollisionsberechnungen, bietet sich an, die 6 Begrenzungspolygone (Quads) mit den entsprechenden Vertices und evtl. den Flächennormalen im voraus zu berechnen. Damit wird der Zugriff während der Laufzeit verkürzt und vereinfacht.

Zylinder und Kegel werden meistens in der Standardausrichtung mit lotrechter Achse eingesetzt. Hierbei sind drei Parameter ausreichend: Mittelpunkt der Grundfläche, Radius des Grundkreises und Höhe des Körpers (Länge der Hauptachse).

Die bisher aufgeführten Parameter beschreiben den Hüllkörper isoliert, es muss schließlich noch die Relation zum eingeschlossenen Objekt hergestellt werden. Objekte erhalten bei ihrer Erstellung im 3D-Programm einen eindeutigen Bezugspunkt, nämlich den lokalen Koordinatennullpunkt. Alle Vertices beziehen sich darauf, und auch die Positionierung in der Szenerie erfolgt damit. Oft, aber nicht immer kann dieser Punkt zugleich der Positionspunkt des Hüllkörpers sein. Bei Abweichungen muss folglich ein Verschiebungsvektor als zusätzlicher Parameter hinzukommen.

• ) Anmerkung: Je nach Programmkonzept können zur Speicherung von Objekt-Ausrichtungen auch Quaternionen oder Matrizen verwendet werden.

Hüllkörper als Rotations- und Skalierungsraum

Häufig möchte man ein Objekt mehrfach in einer Szenerie verwenden, und das mit unterschiedlichen Rotationen und/oder Skalierungen. Das bedeutet, dass auch der Hüllkörper zusammen mit dem eingeschlossenen Objekt rotiert und skaliert werden muss. Jede Objektinstanz erhält demnach einen speziellen Hüllkörper.

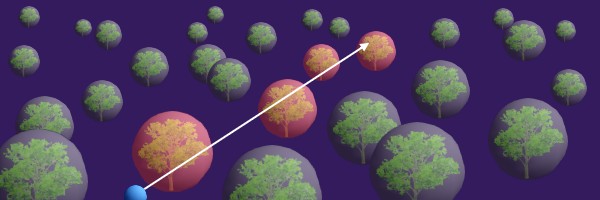
Wenn aber die Hüllkörper lediglich als Container dienen und nicht für exakte Berechnungen herhalten müssen, lässt sich die Prozedur vereinfachen. Es wird ein Hüllkörper konstruiert, der zwar entsprechend skaliert, ansonsten aber so bemessen wird, dass er Raum für beliebige Rotationen lässt. Bei geringem Skalierungsbereich kann man darüber hinaus auf die Skalierung verzichten und den größten (möglichen oder erlaubten) Faktor zugrunde legen.

Das Ergebnis ist naturgemäß eine Kugel, von der allerdings nur die obere Hälfte genutzt wird. Der Bezugspunkt von Objekten liegt normalerweise unten, damit das Objekt direkt auf die Oberfläche der Szenerie gesetzt werden kann. Dieser Bezugspunkt ist nun gleichzeitig der Mittelpunkt der Hüllkugel.

Dass die Hüllkugel im Vergleich zum Objekt oft übertrieben groß ausfällt, stört natürlich. Wenn die Objekte nicht allzu dicht beieinander liegen, muss sich das jedoch nicht nachteilig auswirken.