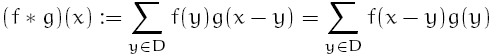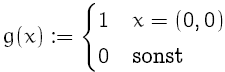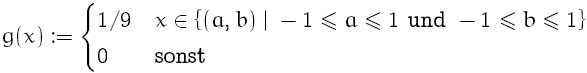Convolution-Filter: Unterschied zwischen den Versionen
(Ein bischen Mathematik) |
K (→Ein klein wenig Theorie) |
||
| Zeile 12: | Zeile 12: | ||
== Ein klein wenig Theorie == | == Ein klein wenig Theorie == | ||
Ein (diskreter) Faltungskerne g wird auf ein Signal f (z.B. ein Bild) durch eine einfache Rechenvorschrift angewendet: | Ein (diskreter) Faltungskerne g wird auf ein Signal f (z.B. ein Bild) durch eine einfache Rechenvorschrift angewendet: | ||
| + | |||
[[Bild:Faltung_Math.png]] | [[Bild:Faltung_Math.png]] | ||
| + | |||
Hierbei ist D der gemeinsame Definitionsbereich von f und g. Für Bilder bietet sich hier z.B. das kartesische Produkt der ganzen Zahlen Z^2 an. Was also passiert hier? Nehmen wir zuerst den einfachsten Faltunskern | Hierbei ist D der gemeinsame Definitionsbereich von f und g. Für Bilder bietet sich hier z.B. das kartesische Produkt der ganzen Zahlen Z^2 an. Was also passiert hier? Nehmen wir zuerst den einfachsten Faltunskern | ||
| + | |||
[[Bild:Faltung_OhneEffekt.png]] | [[Bild:Faltung_OhneEffekt.png]] | ||
| + | |||
Setzt man diese Funktion in die obige Definition ein, so passiert dem Signal: gar nichts, denn die Summe fällt zusammen und es bleibt immer nur g(0)*f(x) = f(x) stehen. Erweitert man nun den Support (der Bereich, auf dem g nicht 0 ist) des Faltungskern vom Punkt 0 auf auf den Bereich [-1,1]^2 | Setzt man diese Funktion in die obige Definition ein, so passiert dem Signal: gar nichts, denn die Summe fällt zusammen und es bleibt immer nur g(0)*f(x) = f(x) stehen. Erweitert man nun den Support (der Bereich, auf dem g nicht 0 ist) des Faltungskern vom Punkt 0 auf auf den Bereich [-1,1]^2 | ||
| + | |||
[[Bild:Faltung_Tiefpass.png]] | [[Bild:Faltung_Tiefpass.png]] | ||
| − | so addiert man durch die Faltung an einer Stelle x des Bildes f mit g, auch alle direkt benachbarten Bildpunkte auf und mischt sie zusammen - dabei verschwinden natürlich die Details im Bild (diese haben in der Fourier Transformierten eine hohe Frequenz) und es bleiben nur die Informationen, die sich lokal um unseren Bildpunkt nicht so sehr ändern, also eine niedrige Frequenz haben; | + | |
| − | Andererseits erkennt man, daß der Faltungskern g beschreibt, mit welchen Faktoren benachbarte Bildpunkte im Ergebnis zusammengeblendet werden. Der Bereich in dem g gleich 0 ist, ist damit aber völlig unerheblich und man beschränkt sich zum | + | so addiert man durch die Faltung an einer Stelle x des Bildes f mit g, auch alle direkt benachbarten Bildpunkte auf und mischt sie so zusammen - dabei verschwinden natürlich die Details im Bild (diese haben in der Fourier Transformierten eine hohe Frequenz) und es bleiben nur die Informationen, die sich lokal um unseren Bildpunkt nicht so sehr ändern, also eine niedrige Frequenz haben; g unterdrückt also die hohen Frequenzen und lässt die niedrigen durch - weshalb g ein Tiefpass-Filter genannt wird. |
| + | Andererseits erkennt man, daß der Faltungskern g beschreibt, mit welchen Faktoren benachbarte Bildpunkte im Ergebnis zusammengeblendet werden. Der Bereich in dem g gleich 0 ist, ist damit aber völlig unerheblich und man beschränkt sich zum Speichern des Kerns auf dessen Support, was zu den bereits erwähnten Darstellungen mit Matrizen führt. | ||
== Beispiel Faltungskerne == | == Beispiel Faltungskerne == | ||
Version vom 3. April 2008, 08:21 Uhr
Inhaltsverzeichnis
Convolution-Filter
In der Bildverarbeitung spricht man auch von Faltungskernen, in Gimp ist der Begriff Faltungsmatrix üblich.
Ein Convolution-Filter ist ein ein- bzw. zweidimensionales Array, dessen Werte Gewichtungen darstellen. Bei Ausführung der Filterung wird das Array Pixel für Pixel auf ein Bild bzw. eine Textur anwendet. Dabei werden die Werte im Array mit den Farben des Bildes multipliziert und zusammenaddiert.
Ist z.B. ein 3x3-Array als Filterkernel gesetzt, so wird der Mittelpunkt auf jedes Pixel gesetzt und die 8 Nachbarpixel um diesen herum mit den Werten in der Matrix verrechnet. Das Ergebnis dieser Rechnung wird in das Pixel gespeichert was im Zentrum der Matrix lag.
Damit lassen sich interessante Effekte wie z.B. Kontraste, Schärfung, Weichzeichnen, Kantenextraktion(Embossing) oder Glowing erzielen.
Ein klein wenig Theorie
Ein (diskreter) Faltungskerne g wird auf ein Signal f (z.B. ein Bild) durch eine einfache Rechenvorschrift angewendet:
Hierbei ist D der gemeinsame Definitionsbereich von f und g. Für Bilder bietet sich hier z.B. das kartesische Produkt der ganzen Zahlen Z^2 an. Was also passiert hier? Nehmen wir zuerst den einfachsten Faltunskern
Setzt man diese Funktion in die obige Definition ein, so passiert dem Signal: gar nichts, denn die Summe fällt zusammen und es bleibt immer nur g(0)*f(x) = f(x) stehen. Erweitert man nun den Support (der Bereich, auf dem g nicht 0 ist) des Faltungskern vom Punkt 0 auf auf den Bereich [-1,1]^2
so addiert man durch die Faltung an einer Stelle x des Bildes f mit g, auch alle direkt benachbarten Bildpunkte auf und mischt sie so zusammen - dabei verschwinden natürlich die Details im Bild (diese haben in der Fourier Transformierten eine hohe Frequenz) und es bleiben nur die Informationen, die sich lokal um unseren Bildpunkt nicht so sehr ändern, also eine niedrige Frequenz haben; g unterdrückt also die hohen Frequenzen und lässt die niedrigen durch - weshalb g ein Tiefpass-Filter genannt wird. Andererseits erkennt man, daß der Faltungskern g beschreibt, mit welchen Faktoren benachbarte Bildpunkte im Ergebnis zusammengeblendet werden. Der Bereich in dem g gleich 0 ist, ist damit aber völlig unerheblich und man beschränkt sich zum Speichern des Kerns auf dessen Support, was zu den bereits erwähnten Darstellungen mit Matrizen führt.
Beispiel Faltungskerne
Tiefpass / Mittelwert
Es wird der Mittelwert zwischen der Farbe des aktuellen Pixels und seinen 8 Nachbarn berechnet und dem aktuellen Pixel zugewiesen. In den Zahlen drück sich dies so aus, dass alle 9 Matrix-Einträge gleichstark (1/9) in die resultierende Farbe eingehen.
1/9 1/9 1/9 1/9 1/9 1/9 1/9 1/9 1/9
Schärfung
0 -1 0 -1 5 -1 0 -1 0
Horizontale Schärfung
-1 -1 -1 2 3 2 -1 -1 -1
Embossing (Kantenfindung)
Richtung links oben
1 0 0 0 0 0 0 0 -1
Richtung rechts unten
-1 0 0 0 0 0 0 0 1
Sobel-Filter
-1 -2 -1 0 1 0 1 2 1
Gaussian Blur
0.00000067 0.00002292 0.00019117 0.00038771 0.00019117 0.00002292 0.00000067 0.00002292 0.00078633 0.00655965 0.01330373 0.00655965 0.00078633 0.00002292 0.00019117 0.00655965 0.05472157 0.11098164 0.05472157 0.00655965 0.00019117 0.00038771 0.01330373 0.11098164 0.22508352 0.11098164 0.01330373 0.00038771 0.00019117 0.00655965 0.05472157 0.11098164 0.05472157 0.00655965 0.00019117 0.00002292 0.00078633 0.00655965 0.01330373 0.00655965 0.00078633 0.00002292 0.00000067 0.00002292 0.00019117 0.00038771 0.00019117 0.00002292 0.00000067
OpenGL-Befehle
glConvolutionFilter1D, glConvolutionFilter2D, glConvolutionParameter, glGetConvolutionFilter, glGetConvolutionParameter
Siehe Auch
Bildverarbeitungsscript von Dr. Steinmüller TU Chemnitz (deutsch) Ausführliche Beschreibung von Faltungskernen ab Kapitel 2.3
[http://www.vbaccelerator.com/home/VB/Code/vbMedia/Image_Processing/Blurring__Sharpening_and_Embossing/article.asp Beschreibung einiger Faltungskerne (englisch)