TBN Matrix: Unterschied zwischen den Versionen
Oc2k1 (Diskussion | Beiträge) (→Wie kann die TBN Matrix berechnet werden) |
Oc2k1 (Diskussion | Beiträge) (→Wie kann die TBN Matrix berechnet werden) |
||
| Zeile 22: | Zeile 22: | ||
Da Av = Ev ist. | Da Av = Ev ist. | ||
| + | |||
Muss (E-B)*(B-C).v = (C-B)*(B-A).v sein. Das lösen wir Nach E auf: | Muss (E-B)*(B-C).v = (C-B)*(B-A).v sein. Das lösen wir Nach E auf: | ||
| Zeile 29: | Zeile 30: | ||
E = B + (C-B)*((B-A)/(B-C)).v | E = B + (C-B)*((B-A)/(B-C)).v | ||
| + | |||
Tangent = (E-A)/(E-A).u | Tangent = (E-A)/(E-A).u | ||
| Zeile 34: | Zeile 36: | ||
D = C + (B-C)*((C-A)/C-B)).u | D = C + (B-C)*((C-A)/C-B)).u | ||
| + | |||
Bitangent = (D-A)/(D-A).v | Bitangent = (D-A)/(D-A).v | ||
Version vom 18. Juni 2006, 20:23 Uhr
Bitte haben Sie etwas Geduld und nehmen Sie keine Änderungen vor, bis der Artikel hochgeladen wurde. |
Was ist die TBN Matrix
Die TBN Matrix ist nach ihren Komponenten benannt, den Vektoren Normal, Bitangent (auch Binormal) und Tangent.
Wie kann die TBN Matrix berechnet werden
Da die einzigsten Erklärungen, die mir bis jetzt bekannt sind auch Englisch sind und dazu mit sehr unverständlichen Formeln gewürzt sind, versuch ich das ganze mal so zu beschreiben, dass es auch von normalen Programieren verstanden wird.
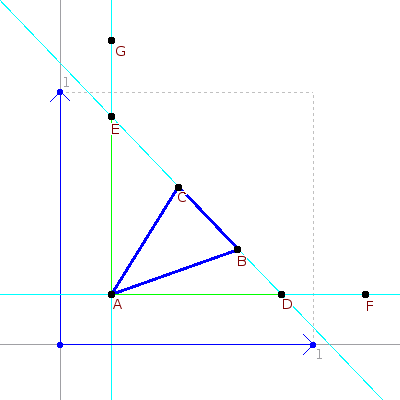
Bekannt sind zum Berechnen der TBN Matrix nur die Textur und Weltkoordinaten des Dreiecks ABC, welches oben abgebildet ist. Die beiden blauen Vektoren, die auf das graue Kreutz gezeichnet sind spannen zusammen mit der grauen gestrichelten Linie die Textur auf. Der Horizontale Vektor repäsentiert Zugleich die U Achse der Textur, als auch den Tangentvektor. Der Vertikale entspricht der V Achse und Bitangent. Im Texturspace sieht es jetzt sehr leicht aus, das Problem ist jedoch, dass wir die TBN Matrix aus der Sicht des Worldspaces beschreiben müssen. Die einzigen Punkte, die wir aus dem Worldspace kennen sind jedoch nur AB und C.
Die Berechnung von Tangent und Bitangent ist fast gleich da nur andere Komponeten eingesetz werden müssen. Erst einmal nur Tangent:
Der Tangend entspricht dem Vektor (G-A), Da wir ih nicht direkt kennen müssen wir erst (E-A) berechnen. Um den Punkt E zu bekommen muss der Vektor (C-B) so weit verlänger werden, das er (E-B) ergibt. Um diesen Verlängerungsfakor zu Berechnen müssen wir die V Komonenten der Texturkoordinaten zu hilfe nehmen:
Da Av = Ev ist.
Muss (E-B)*(B-C).v = (C-B)*(B-A).v sein. Das lösen wir Nach E auf:
E = B + (C-B)*((B-A)/(B-C)).v
Da der Vektor (E-A) kleiner als 1.0 (im Texturspace!!!) ist. Müssen wir ihn noch durch Teilen von (E-A).u auf die Richtige Länge bringen:
E = B + (C-B)*((B-A)/(B-C)).v
Tangent = (E-A)/(E-A).u
Bitantent lässt sich berechnen, in dem B;C, D;E, F;G und u;v getauscht werden:
D = C + (B-C)*((C-A)/C-B)).u
Bitangent = (D-A)/(D-A).v
Die am einfachsten zu berechnende Komponente ist der Normalvektor, er ist quasi unabhängig von den Texturkoordinaten. Es gibt zwei Möglichkeiten ihn zu berechnen. Entweder das Kreutzprodukt der Verktoren (C-A)x(B-A) oder das Kreutzprodukt von Tangent x Bitangent.
Wären der Normalvektor bei der Lichtberechnung einfach normalisiert wurde, ist dass bei der TBN Matrix nur sinvoll, wenn alle drei Komponenten normalisiert werden. In diesem Fall ist die Matrix aber nur noch eingeschränkt zu verwendbar. Wenn die Matrix nur zum Rotieren von Normalvektoren einer Normalmap benöigt wird, ist es sogar Erwünscht, da sich dann deren Länge nicht ändert.
Sobald aber eine Textur 3Dimensional gemappt wird. Sollte die TBN Matrix die Weltkoordinaten korrekt auf den Texturspace abbilden. Dies gilt aber hauptsächlich nur für Paralax und Reliefmapping.