Interpolation: Unterschied zwischen den Versionen
Lyr (Diskussion | Beiträge) (→Rechenbeispiel: Grafik eingefügt) |
Lyr (Diskussion | Beiträge) (→Hermite Kurven: Grafik eingefügt) |
||
| Zeile 165: | Zeile 165: | ||
f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2 | f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2 | ||
Da die Dimensionen hier ebenfalls unabhängig sind, können Hermit-Kurven auf beliebig viele Dimensionen erweitert werden. | Da die Dimensionen hier ebenfalls unabhängig sind, können Hermit-Kurven auf beliebig viele Dimensionen erweitert werden. | ||
| + | |||
| + | Das Ergebnis sieht nun folgendermaßen aus: | ||
| + | |||
| + | [[Bild:InterpolationBsp3.PNG]] | ||
| + | |||
| + | ''Oben angegebenes Beispiel grafisch dargestellt. Die beiden Punkte sind rot dargestellt, die beiden Tangenten sind als blaue Geraden eingezeichnet. Die Kurve beinhaltet alle Punkte der gegebenen Funktionen für t im Wertebereich [0|1].'' | ||
=Tangenten von Kurven= | =Tangenten von Kurven= | ||
Version vom 5. November 2005, 01:14 Uhr
Bei Interpolationsverfahren geht es darum, aus wenigen Werten beliebig viele Werte zu generieren. Da die gegebenen Werte - wo Interpolation nötig ist - meistens als Stichproben gesehen werden können, werden verschiedenste Verfahren benötigt um auch die nicht gegebenen Werte den Ansprüchen entsprechend zu berechnen. Die Ansprüche variieren hierbei etwas anhand der Geschwindigkeitsanforderungen, des Zahlenraumes und nicht zuletzt anhand der Art und Weise wie man interpolieren möchte.
Inhaltsverzeichnis
Polynom Interpolationen
Wenn man N gegebene Werte hat, so kann man diese mit einem Polynom (N-1)ten Grades interpolieren. Eine Polynom Interpolationen besitzen die allgemeine Form:
I = (t^n)*Fn + (t^(n-1))*F(n-1) + ... + t*F1 + F0
Wobei:
t ... die Interpolationsposition im Wertebereich [0|1] Fx ... ein konstanter Wert oder Faktor (oder allgemein ein m-Dimensionaler Vektor) I ... das interpolierte Ergebnis, was ebenfalls ein einzelner Wert oder ein Vektor sein kann.
Durch die Vektor-Schreibweise sollte bereits klar sein, dass Polynom-Interpolationen für jede Dimension extrig berechnet werden, und somit auf beliebig viele Dimensionen erweiterbar sind.
Lineare Interpolation
Allgemein
Die einfachste Form einer Polynom-Interpolation ist die lineare Interpolation. Hierbei sind nur 2 Werte gegeben, somit kann man diese Werte mit einem Polynom ersten Grades interpolieren. Dieses ist (wie unschwer zu erraten) eine Gerade der Form:
I = t*F1 + F0
Diese (eher ungewöhnliche) Form der Geradengleichung entspricht der oben angegebenen Polynom-Interpolation in beliebiger Dimension. Die Berechnung der Faktoren Px erfolgt hier für jede Dimension getrennt. Gegeben seien 2 m dimensionale Punkte (A1, A2, ..., A(m-1), Am) und (B1, B2, ..., B(m-1), Bm). Nun lässt sich für jede Dimension d ein einfaches Gleichungssystem aufstellen:
Ad = 0*F1d + F0d Bd = 1*F1d + F0d
da wir mit einem Interpolationswert von 0 den ersten Punkt (A) erhalten wollen und einem Interpolationswert von 1 den zweiten Punkt (B) möchten. Dies umgeformt auf P1d und P0d ergibt:
F0d = Ad F1d = Bd - Ad
Diesen Rechenschritt wiederholen wir für jede Dimension.
Rechenbeispiel
Wir wollen 2 Punkte im 3 dimensionalen Raum interpolieren:
A: (2|5|0) B: (4|1|8)
Wir berechnen uns die Vektoren P1 und P0 wie oben angegeben, wobei x die erste und z die dritte Dimension dar stellen soll:
F0x = Ax = 2 F1x = Bx - Ax = 2 F0y = Ay = 5 F1y = By - Ay = -4 F0z = Az = 0 F1z = Bz - Az = 8
Somit erhalten wir die unsere Interpolationsgleichung:
I(x|y|z) = t * (2|-4|8) + (2|5|0)
Das Ergebnis sieht nun folgendermaßen aus:
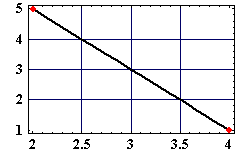
2 dimensionale Version des obigen Beispieles. Die gegebenen Punkte sind somit A(2|5) und B(4|1). Diese Punkte sind in rot dargestellt. Die Gerade beinhaltet alle Punkte für die gegebene Formel mit t im Wertebereich [0|1]
Polynome höheren Grades
Allgemein
Wie euch vielleicht schon bei der linearen Interpolation aufgefallen ist, ist eine Reihung der Punkte (vorher nur 2) erforderlich. Welcher PUnkt soll das Ergebnis mit t = 0 sein? Und welcher mit t=1? Wenn man mehr als 2 Punkte gegeben hat, so benötigt man zusätzlich noch die Informationen für welches t die beiden neuen Punkte gelten sollen. Meistens interpoliert man hier die Werte für t linear. Das heißt bei N gegebenen Punkten, soll der x-te Punkt für den t-Wert
t(Px) = x / (N-1) + 0
gegeben werden. Wobei:
t(Px) ... der t-Wert für den x-ten Punkt
Das (N-1) der Gleichung wird uns noch länger verfolgen, deshalb werden wir im weiteren Verlauf N-1 als n bezeichnen. Hier noch kurz die Anmerkung, dass man bei einem gegebenen Punkt natürlich keine Parameter benötigt sondern der Punkt immer gleich ist. Man kann sich dies (und alles darauffolgende) auch so vorstellen, dass wir den ersten gegebenen Punkt F0 als 0-Punkt annehmen und erst am "Ende" F0 addieren. Aus dieser Sichtweise heraus bekommen wir unser n = N-1.
Nun lässt sich wiederum das allgemeine (lineare) Gleichungssystem auffstellen:
P0 = t(P0)^n * Fn + t(P0)^(n-1) * F(n-1) + ... + t(P0) * F1 + F0 P1 = t(P1)^n * Fn + t(P1)^(n-1) * F(n-1) + ... + t(P1) * F1 + F0 ... Pn = t(Pn)^n * Fn + t(Pn)^(n-1) * F(n-1) + ... + t(Pn) * F1 + F0
Wobei:
Px ... der x-te Punkt t(Px) ... der t-Wert für den x-ten Punkt Fy ... der zu berechnende Faktor
Also ein Gleichungssystem mit n unbekannten und n (linear unabhängigen) Gleichungen, welches sich demnach eindeutig lösen lässt. Wobei dieses Gleichungssystem wiederum für jede Dimension extrig aufgestellt und berechnet werden muss! Da man (eindeutig lösbare) Gleichungssystem recht angenehm durch Matrizen-Mathematik lösen kann, empfiehlt sich auch folgende Schreibweise:
P = M * F
Wobei:
P ... ein N dimensionaler Vektor der die gegebenen Werte für den jeweiligen Punkt beinhaltet M ... eine NxN Matrix welche die t(Px)^y beinhaltet F ... ein N dimensionaler Vektor der die zu berechnenden Faktoren erhält und N ... wie gehabt die Anzahl der gegebenen Punkte und n = N - 1
Dies kann man nun umformen in:
M^-1 * P = F
Wobei:
M^-1 ... die inverse von M ist
Dadurch erhält man alle Werte Fy die man benötigt und kann somit für ein gegebenes t wiederum in die allgemeine Form:
I = (t^n)*Fn + (t^(n-1))*F(n-1) + ... + t*F1 + F0
einsetzen.
Rechenbeispiel
Wir wollen über 4 Punkte eine Polynominterpolation im 2 dimensionalen Raum. Diese sind:
P0: (5|3) P1: (1|4) P2: (4|2) P3: (1|2)
Wir legen nun zuerst wieder die t-Werte für die Punkte fest, und sagen:
P0 bei t=0 P1 bei t=1/3 P2 bei t=2/3 P3 bei t=1
Und berechnen uns nun die Matrix M mit diesen t-Werten:
| 0^3 0^2 0^1 1 |
M = | 0.33^3 0.33^2 0.33 1 |
| 0.66^3 0.66^2 0.66 1 |
| 1^3 1^2 1^1 1 |
Und berechnen uns nun die inverse M^-1:
| -4.5 13.5 -13.5 4.5 |
M^-1 = | 9 -22.5 18 -4.5 |
| -5.5 9 -4.5 1 |
| 1 0 0 0 |
Nun nehmen wir den P-Vektor der ersten Dimension:
Px = (5|1|4|1)
und multiplizieren ihn mit der Matrix wodurch wir
Fx = M^-1 * Px = (-58.5|90|35.5|5)
erhalten. Nun das selbe für die zweite Dimension:
Py = (3|4|2|2)
und wiederum
Fy = M^-1 * Py = (22.5|-36|12.5|3)
Somit ist unsere endgültige Formel für die Interpolation:
Ix = -58.5 * t^3 + 90 * t^2 - 35.5 * t + 5 Iy = 22.5 * t^3 - 36 * t^2 + 12.5 * t + 3
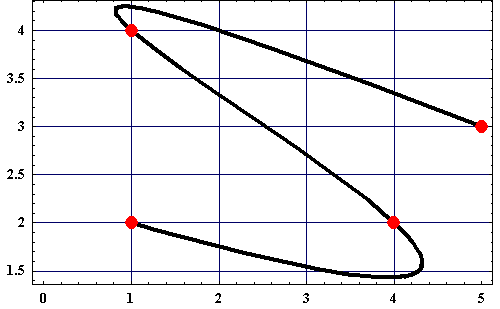
Das Ergebnis sieht nun folgendermaßen aus:
Oben angegebenes Beispiel grafisch dargestellt. Die Punkte P0 bis P3 sind rot dargestellt. Die Kurve beinhaltet alle Punkte der gegebenen Funktionen für ( Ix , Iy ) mit t im Wertebereich [0|1].
Kurven mit gegebenen Tangenten
Wir haben die oben gegebene Polynom-Gleichung für N Punkte. Wenn wir nun zusätzlich J Tangenten angeben möchten, so haben wir natürlich J zusätzliche Gleichungen und benötigen ein Polynom (N+K-1)ten Grades. Als erstes stellen wir wiederum eine derartige Polynom-Gleichung auf, jedoch mit dem Unterschied das wir dies gleich mit dem (N+J-1)ten Grad machen. Des weiteren müssen wir für jede Tangente Festlegen bei welchem t^x wir sie einbrigen möchten. Der Einfachheit halber wird hier die Reihung: zuerst die Punkte (also einem t^x mit höherem x) und danach die Tangenten (also einem t^x mit niedrigerem x als die Punkte bis hin zu x=0) verwendet. Daraus ergibt sich die allgemeine Form für die Punkte:
P0 = t(P0)^(n+J) * F(n+J) + t(P0)^(n+J-1) * F(n+J) + ... + t(P0)^(J+1) * F(J+1) + t(P0)^J * F(J) + t(P0)^(J-1) * F(J-1) + t(P0)^(J-2) * F(J-2) + ... + t(P0) * F1 + F0 P1 = t(P1)^(n+J) * F(n+J) + t(P1)^(n+J-1) * F(n+J) + ... + t(P1)^(J+1) * F(J+1) + t(P1)^J * F(J) + t(P1)^(J-1) * F(J-1) + t(P1)^(J-2) * F(J-2) + ... + t(P1) * F1 + F0 ... Pn = t(Pn)^(n+J) * F(n+J) + t(Pn)^(n+J-1) * F(n+J) + ... + t(Pn)^(J+1) * F(J+1) + t(Pn)^J * F(J) + t(Pn)^(J-1) * F(J-1) + t(Pn)^(J-2) * F(J-2) + ... + t(Pn) * F1 + F0
Wobei:
Px ... der x-te Punkt t(Px) ... der t-Wert für den x-ten Punkt F(n+J) bis F(J) ... der zu berechnende Faktor für den (N-1)ten Punkt F(J-1) bis F(0) ... der zu berechnende Faktor für die J-te Tangente
Nun benötigen wir natürlich noch weitere Gleichungen für die Tangenten um das Gleichungssystem eindeutig lösbar zu machen. Eine Tangente K (hier wird bewusst K und nicht T gewählt) für den Xten Punkt lässt sich durch eine Ableitung nach t berechnen:
K(Px) = (n+J) * t(Px)^(n+J-1) * F(n+J) + (n+J-1) * t(Px)^(n+J-2) * F(n+J-1) + ... + (J+1) * t(Px)^(J) * F(J+1) + J * t(Px)^(J-1) * F(J) + (J-1) * t(Px)^(J-2) * F(J-1) + (J-2) * t(Px)^(J-3) * F(J-2) + ... + t(Px) * F2 + F1 + ( 0 * F0 )
Mit diesen Gleichungssystemen können wir wiederum eine Matrix formen, diese invertieren und los legen. Aber (meines Erachtens) erklärt sich dies am besten an einem Beispiel.
Hermite Kurven
Hermite Kurven sind Interpolationsfunktionen wo der Anfangs- und Endpunkt eine bestimmte Tangente aufweist. Üblicherweise werden Hermite Kurven zusätzlich noch auf 2 gegebene Punkte beschränkt, was wir hier der Einfachheit halber beibehalten wollen. Wir haben 2 Punkte, 2 Tangenten wodurch wir auf ein Polynom (N+J-1) = (2+2-1) = 3ten Grades kommen. Alse stellen wir eine Polynomgleichung für 2 gegebene Punkte auf, wobei der erste Punkt den Zeitpunkt 0 und der zweite Punkt den Zeitpunkt 1 erhält. Dadurch kommen wir auf zwei triviale Gleichungen:
P0 = 0 * F(3) + 0 * F(2) + 0 * F(1) + 1 * F(0) P1 = 1 * F(3) + 1 * F(2) + 1 * F(1) + 1 * F(0)
Nun noch die Tangentengleichungen die sich aus der oben angegebenen K(Px) - Formel ergeben:
K0 = 0 * F(3) + 0 * F(2) + 1 * F(1) + 0 * F(0) K1 = 3 * F(3) + 2 * F(2) + 1 * F(1) + 0 * F(0)
Dies ist unser lineares Gleichungssystem woraus wir wiederum unsere Matrix gewinnen:
| 0 0 0 1 |
M = | 1 1 1 1 |
| 0 0 1 0 |
| 3 2 1 0 |
Und natürlich die Formel:
W = M * F
Wobei:
W ... ein Vektor ist der die Werte P0, P1, K0, K1 (in dieser Reihenfolge) beinhaltet M ... die oben gegebene Matrix F ... der Vektor der die zu berechnenden Werte beinhaltet.
Diese Matrix invertiert ergibt:
| 2 -2 1 1 |
M^-1 = | -3 3 -2 -1 |
| 0 0 1 0 |
| 1 0 0 0 |
Somit können wir den F-Vektor berechnen durch
M^-1 * W = F
Wenn wir nun also für W die Werte (2,3,-1,1) hätten, wobei hier
2 ... der erste Punkt 3 ... der zweite Punkt -1 ... die Tangente für den ersten Punkt 1 ... die Tangente für den zweiten Punkt
so ergeben sich daraus die Faktoren:
F = M^-1 * W = (-2,4,-1,2)
Wodruch wir für unsere Kurve folgende Formel erhalten:
f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2
Da die Dimensionen hier ebenfalls unabhängig sind, können Hermit-Kurven auf beliebig viele Dimensionen erweitert werden.
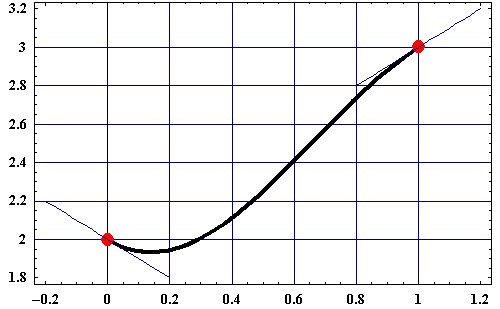
Das Ergebnis sieht nun folgendermaßen aus:
Oben angegebenes Beispiel grafisch dargestellt. Die beiden Punkte sind rot dargestellt, die beiden Tangenten sind als blaue Geraden eingezeichnet. Die Kurve beinhaltet alle Punkte der gegebenen Funktionen für t im Wertebereich [0|1].
Tangenten von Kurven
Besitzt man die Funktion für eine Kurve so lässt sich die Tangente durch das differenzieren dieser Funktion ermitteln. Aus unserem vorigen Beispiel wäre dies:
f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2 f'(t) = -6 * t^2 + 8 * t - t
Da die Dimensionen einer derartigen Kurve wie gesagt unabhängig voneinander behandelt werden können, kann man dadurch die Tangente in der entsprechenden Dimension erhalten.
Interpolierte Flächen
Bisher wurden ausschließlich Kurven betrachtet. Aus Kurven lassen sich jedoch ohne größere Umstände auch Flächen bilden. Hier hat man zwei (unterschiedliche) t-Werte und eine Matrix von Punkten gegeben, wobei jeder Punkt gegebenenfalls noch 1 oder 2 Tangenten besitzen kann. Um einen Punkt einer Fläche zu berechnen interpoliert man zuerst die Punkte für jede Zeile der Punktmatrix. Nachdem man nun die interpolierten Punkte für jede Zeile besitzt kann man sich mit diesen Punkten ein neues Gleichungssystem aufstellen und wiederum eine Kurve bilden. Diese Kurve interpoliert man wiederum mit dem zweiten gegebenen t-Wert. Dies lässt sich auf beliebig viele Dimensionen nach dem gleichen Schema erweitern, üblicherweise wird dies jedoch nur für Oberflächen (also 2D) benötigt.
Normalvektoren
Besitzt man Flächen und berechnet sie nach dem gegebenen Schema, so berechnet man sich zuerst auch mehrere Kurven von denen man die Tangenten berechnen kann. Interpoliert man nun diese Tangenten mit der gleichen Kurvenfunktion wie die resultierenden Punkte, und berechnet sich aus der resultierenden Kurvenfunktion ebenfalls die Tangente, so erhält man 2 Tangenten. Aus diesen beiden Tangenten kann nun mit einem Kreuzprodukt ein Normalvektor errechnet werden.
ACHTUNG: auf Richtigkeit überprüfen
Kurvenlängen-Interpolation
Es könnte erwünscht sein (beispielsweise für Kamerafahrten, Keyframe Interpolationen jeglicher Art oder auch bei der Interpolation von Positionsangaben die man beispielsweise über ein Netzwerk erhält), dass man über keine fixe Achse t interpolieren möchte, sondern über die Kurvenlänge. Die Kurvenlänge kann man sich hierbei als den tatsächlich zurückgelegten Weg vorstellen. Die Länge einer Kurve f bis zu einem Punkt t im Bereich [0,1] wird berechnet durch:
Länge(t) = Integral[0 bis t]( f'(t) )
Wenn man nun eine bestimmte Kurvenlänge s finden möchte, dann muss man den dazugehörigen Wert t finden wo gilt Länge(t)- s = 0. Da es genau einen Wert t gibt auf den dies zutrifft kann dies beispielsweise durch das Newtonsche Näherungsverfahren erreicht werden, welches in wenigen Iterationsschritten eine sehr präziese Lösung liefert.
ACHTUNG: auf Richtigkeit überprüfen