Perlin Noise: Unterschied zwischen den Versionen
Flo (Diskussion | Beiträge) K (Der Kateogrie Technik oder Algorithmus zugeordnet) |
Flo (Diskussion | Beiträge) K (Der Kategorie Anleitung zugeordnet) |
||
| Zeile 201: | Zeile 201: | ||
Wert = Wert + Offset | Wert = Wert + Offset | ||
| − | [[Kategorie:Technik_oder_Algorithmus]] | + | [[Kategorie:Anleitung]] [[Kategorie:Technik_oder_Algorithmus]] |
Version vom 23. September 2005, 09:30 Uhr
Perlin Noise ist ein Fraktal-Algorithmus welcher mit sehr einfachen Formeln komplexe und theoretisch endlose Gebilde berechnen kann. Da Perlin Noise darauf basiert, scheinbar zufällige Funktionen mit weichen Übergängen (die Steigung kann einen gewissen Wert nicht überschreiten) zu benutzen, eignet er sich sehr gut zur Simulation verschiedenster, natürlicher Phänomene wie Beispielsweise:
- Wolken
- Landschaftshöhen- und auch Texturen
- eventuell auch Texturen wie Wasser, Feuer und ähnliches
Inhaltsverzeichnis
Grundlagen
Perlin Noise basiert auf der Überlagerung von Frequenzen. Bei einer niedrigen Frequenz wird zwischen 2 eher weit voneinander entfernten angegebenen Werten interpoliert. Bei der höchsten (sinnvollen) Frequenz wird für jeden dargestellten Wert (zB jedes Pixel) ein anderer Wert berechnet. Die Werte werden aus Pseudozufallszahlen für eine Positionsangabe gebildet. Die Positionsangabe kann hier eine beliebige Dimension besitzen (beispielsweise 2D für eine Heightmap, 3D für eine Volumentrische Textur, ...). Die Ausgabe ist üblicherweise 1 Wert welcher beliebig interpretiert werden kann.
Zufallswerte aber wie?
Es wird eine Funktion benötigt die für jede Dimension einen Parameter hat und für die gleichen Parameter auch die gleichen Zahlen liefert.
// 1. Dimension function Werte1D(X:Integer):ErgebnisTyp // 2.Dimension function Werte2D(X,Y:Integer):ErgebnisTyp
mit einen Array
Diese Aufgabe kann ein Array erflüllen welcheswelches man zuvor mit Zufallswerten gefüllt hat. also:
Werte1D:array [0..X_Werte_Max] of ErgebnisTyp; Werte2D:array [0..X_Werte_Max,0..Y_Werte_Max] of ErgebnisTyp;
eigene Zufallsfunktion
Ein gängiger Algorithmus sieht beispielsweise so aus:
x := x + Seed; x := ( x shl 13 ) xor x; rand := 1 - ( (x * (x * x * 15731 + 789221) + 1376312589) and $7fffffff) / 1073741824;
Rand liefert hier einen Wert für eine 1 Dimensionale Positionsangabe (X - Ganzzahl) einen Wert zwischen -1 und 1. Für 2 Dimensionen könnte dieser Code folgendermaßen erweitert werden:
n := x + y * 57 + Seed; n := ( n shl 13 ) xor n; rand := 1 - ( (n * (n * n * 15731 + 789221) + 1376312589) and $7fffffff) / 1073741824;
im weiteren wird diese Funktionalität mit Random( Pos ) bzw. Random( PosX, PosY ) verwendet.
Interpolation
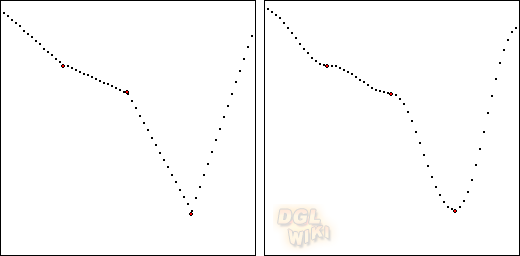
Zwischen den Werten aus dem Array versucht man nun mit einer Interpolation schöne Übergänge zu schaffen. Am schnellsten ist die lineare Interpolation, jedoch kann durch einen Trick auch eine Sinus artige Interpolation sehr schnell ablaufen. Auf den folgenden Bildern sieht man links linear Interpolierte Höhenwerte und auf der rechten seite eine Sinus/Cosinus artige Interpolation. Die größern Punkte entsprechen den im Array abgespeicherten Zufallswerten.
Die Interpolations funktion muss zunächst einmal die beiden zu interpolierenden Werte entgegen nehmen. Zusätzlich muss noch durch mindestens einen weiteren Parameter klar werden, welche Position (im obrigen Bild X) der gesuchte Wert haben soll.
Wäre einem die Ausführgeschwindigkeit egal, könnten die beiden Interpolations Funktionen folgerndermaßen aussehen:
//Hineis: nicht getestet function InterpoliereLinear(Wert1,Wert2,FaktorWert1:Real); // Lineare Interpolation von zwei Werten // FaktorWert1 muss zwischen 0 und 1 liegen begin result := Wert1*FaktorWert1 + Wert2*(1-FaktorWert1); end; function InterpoliereCos(Wert1,Wert2,FaktorWert1:Real); // Cosinus/Sinus artige Interpolation von zwei werten; // FaktorWert muss zwischen 0 und 1 liegen begin result := Wert1*((cos(pi/2*FaktorWert1)+1)/2) + Wert2*(1-(cos(pi/2*FaktorWert1)+1)/2) end;
Jedoch möchte man meistens möglichst schnelle Berechnungen haben. Besonders die Sinus und Cosinus Funktionen können unter Umständen zum Problem werden. Um trotzdem Sinuns- und Cosinus-Interpolation zu erzeugen kann man im Vorraus sich ein Array mit Interpolationswerten anlegen. Da Rechner schneller mit Integerwerten als mit Gleitkommerwerten rechnen werden wir im folgenden Beispiel erstere verwenden.
var
Interpolation:array [0..Interpolation_Bereich-1]of Integer;
//Interpoaltions_Bereich ist legt die Maximale Anzahl an Punkten fest,
// die für zwei Interpolationswerte ermittelt werden können(inklusive Randpunkte).
const
Interpolation_Max = 1000 // * entspricht dem Wert 1.000;
// * je höher dieser Wert deso genauer das Ergebnis.
// * je höher dieser Wert ist deso niedriger müssen
// die Interpolationswerte sein
procedure BeimStart;
begin
{..}
// Im Interpolations Array werden mit den Werten die von Interpolation_Max bis 0 gehen gefüllt.
// wobei Interpolation[0] = Interpolation_Max ist
// und Interploation[high(Interpolation)] = 0 ist
for i := 0 to high(Interpolation) do Interpolation[I] := round((cos(pi/(Interpolation_Bereich-1)*i)+1)/2*Interpolation_Max);
{..}
end;
function Interpoliere(Wert1,Wert2:Integer;Nr,Von:Integer):Integer;
// Interpoliert zwischen 2 Werten
// Nr ist gibt den Punkt an den man ermitteln möchte. Von die Anzahl der Interpolations schrite
var
Wert1_Faktor:Integer;
begin
if Nr > Von then raise ERangeError.CreateFmt('Nr Wert %d nicht in 0..%d',[Nr,Von-1]);
if Von > Interpolations_Bereich raise ERangeError.CreateFmt('Von Wert %d nicht in 0..%d',[0,-1]);
Wert1_Faktor := Interpolation[(Interpolation_Bereich* Nr)div Von];
result := (Wert1*Wert1_Faktor) div Interpolation_Max
+ (Wert2*(1000 - Wert1_Faktor)) div Interpolation_Max;
end;
Dies wäre die Interpolation für eine 1 Dimensionale Positionsangabe. Natürlich müssen aber auch die anderen Dimensionen interpoliert werden. Dies kann aber (wenn gewünscht) ebenfalls mit mehreren Interpolationen von 2 Werten erfolgen
PosX = Ganzzahl( Position.x ) PosY = Ganzzahl( Position.y ) X1 = Interpoliere( Random( PosX, PosY ), Random( PosX, PosY + 1 ), Nachkommateil( Position.y ) ) X2 = Interpoliere( Random( PosX + 1, PosY), Random( PosX + 1, PosY + 1, Nachkommateil( Position.y ) ) Ergebnis = Interpoliere( X1, X2, Nachkommateil( Position.x ) )
Algorithmus
Mit den oben beschriebenen Funktionen ist der Algorithmus recht schnell zu machen.
Die Parameter
Der Perlin Noise Algorithmus erhält üblicherweise folgende Parameter:
- Double: Position (Die Position wird bereits entsprechend skaliert)
- Double: Persistenz (wie stark ist der Einfluss der höheren Frequenzen)
- Wertebereich: Double: Min, Double: Max
- Integer: Rechentiefe (Detailgrad)
- Gegebenenfalls Double: Frequenzfaktor (oder Standard auf 2)
Die Laufzeit für einen berechneten Wert beträgt O( n ) wobei n die Rechentiefe angibt.
Überlagerung der Frequenzen
Es wird für jeden Detailgrad ein Wert berechnet. Da Perlin Noise für einen einzelnen Wert kaum Sinn macht und im Normalfall für mehrere nebeneinander liegende Positionen ein Wert berechnet wird, kann man auch von Frequenzbändern sprechen. Der Code könnte beispielsweise so aussehen:
Wert = 0 Für jeden Detailgrad Wert = Wert + InterpolierterWert( Position * Frequenz ) Frequenz = Frequenz * Frequenzfaktor
Wie hier unschwer zu erkennen ist werden die Werte addiert (also überlagert).

Abb.1: Frequenzbänder für 200 Werte (Pixel).
Frequenzfaktor = 2; Persitenz = 0.5;
Links oben: Frequenz 0.01 (Einheit = Pixel)
Rechts oben: Frequenz 0.02
Links unten: Frequenz 0.04
Rechts unten: überlagerte (addierte) Frequenzbänder (für die ersten 3 Detailgrade)
Rechentiefe
Die Rechentiefe gibt an wie hoch der Detailgrad sein soll. In Abbildung 1 (siehe Frequenzen) wurde beispielsweise eine Rechentiefe von 3 verwendet. Bei einem 2 Dimensionalen Perlin Noise dürfte dies jedoch deutlichere Unterschiede zeigen (siehe Abbildung 2).

Abb. 2: Unterschiedliche Rechentiefen.
Frequenzfaktor = 2; Persitenz = 0.5;
Links oben: Rechentiefe 1
Rechts oben: Rechentiefe 2
Links unten: Rechentiefe 3
Rechts unten: Rechentiefe 4
Persistenz
Die Persistenz gibt an wie stark die höheren Frequenzbänder Einfluss auf das Ergebnis haben sollen. Hierfür erweitern wir den unter Überlagerung der Frequenzen angegebenen Code:
Wert = 0 Faktor = 1 Für Detailgrad = 1 bis Rechentiefe Wert = Wert + InterpolierterWert( Position * Frequenz ) * Faktor Frequenz = Frequenz * Frequenzfaktor Faktor = Faktor * Persistenz

Abb. 3: Unterschiedliche Persitenzen.
Frequenzfaktor = 2; Rechentiefe = 5
Links oben: Persistenz 0.2
Rechts oben: Persistenz 0.4
Links unten: Persistenz 0.6
Rechts unten: Persistenz 0.8
Der Wertebereich
Bisher wurden zwar in den Bildern die Werte korrekt dargestellt, jedoch wurde noch nicht erklärt wie man zu diesen Werten kommt. Wir möchten nun den Code welcher unter Persistenz angegeben wurde so modifizieren, das er Werte für den Wertebereich [Min|Max] liefert. Betrachten wir vorerst was wir alles verwenden:
- InterpolierterWert( Position * Frequenz ): liefert einen Wert im Bereich [-1|1]
- Faktor: zu Beginn 1, wird bei jeden Durchlauf mit Persistenz multipliziert
- Frequenz und Frequenzfaktor: spielen für die Amplitude keine Rolle
Der Gesamtfaktor lässt sich recht einfach berechnen:
Faktor = 1 GesFaktor = 0 Für Deteilgrad = 1 bis Rechentiefe GesFaktor = GesFaktor + Faktor Faktor = Faktor * Persistenz
Mit dem errechneten Gesamtfaktor wissen wir nun, das die Funktion einen Wert im Bereich
[-GesFaktor|+GesFaktor] liefert. Nun brauchen wir nur noch die Amplitude skalieren und einen entsprechenden Offset für das Minimum addieren. Dies sieht im Endeffekt so aus:
Initialisierung:
Bereich = Max - Min; Offset = Min + Bereich * 0.5; GesFaktor = 0; Faktor = 2; für 1 bis Rechentiefe GesFaktor += Faktor Faktor = Faktor * Persistenz Tiefe_1_Amplitude = Bereich / GesFaktor
Berechnung eines Wertes:
Wert = 0 Faktor = Tiefe_1_Amplitude Frequenz = 1 Für Detailgrad = 1 bis Rechentiefe Wert = Wert + InterpolierterWert( Position * Frequenz ) * Faktor Frequenz = Frequenz * Frequenzfaktor Faktor = Faktor * Persistenz Wert = Wert + Offset