Matrix: Unterschied zwischen den Versionen
(Kleine Verbesserung) |
() |
||
| Zeile 3: | Zeile 3: | ||
===Begriffs-Erklärung=== | ===Begriffs-Erklärung=== | ||
| − | Eine Matrix ist eigentlich nichts anderes als das was man in der Programmierung als zwei | + | Eine Matrix ist eigentlich nichts anderes als das was man in der Programmierung als zwei dimensionales Array(Feld) versteht. Allerdings wird diese tabellenartige Schreibweise gerne für schöne Rechnungen genutzt |
<br> | <br> | ||
Version vom 29. Oktober 2004, 18:14 Uhr
Inhaltsverzeichnis
Matrix(Plural Matrizen)
Begriffs-Erklärung
Eine Matrix ist eigentlich nichts anderes als das was man in der Programmierung als zwei dimensionales Array(Feld) versteht. Allerdings wird diese tabellenartige Schreibweise gerne für schöne Rechnungen genutzt
Die drei OpenGL Matrizen
In OpenGL gibt es drei Matrizen welche alle mit Hilfe von glTranslate, glScale, glRotate bearbeitet werden können. Welche Matrix von diesen Funktionen beeinfusst werden soll, kann mit glMatixMode festgelegt werden.
Das sind die 3 Matrizen:
GL_PERSPECTIVE
Sollte nur für die festlegung der Perspective genutzt werden.
GL_MODELVIEW
Legt Position und Größe des zu zeichnenden Primitiven fest
GL_TEXTURE
Beinhaltet Informationen wie Texturen dargestellt werden.
Aufbau einer OpenGL-Matrix
Möchte man mit OpenGL an einer bestimmten Stelle etwas zeichnen, so kann man mit Hilfe von glTranslate und glRotate die Modelview-Matrix so manipulieren, dass etwa der mit glVertex übergebene Eckpunkt (0/0/0) im Weltkoordinaten System nicht mehr in der Mitte liegt. Alle Punkte erscheinen scheinbar in einen zweiten Koordinaten System welches etwas verdreht,vegrößert oder verrutsch liegen kann.
Dieses zweite Koordinaten-System wird durch eine Matrix (einem zwei demensionenlen Array mit vier Spalten und Zeilen) festgehalten.
Damit besser verstanden werden kann wie dies funktioniert, wird die Funktionsweise erstmal anhand eines zwei demensionalen Koordinaten System demonstiert.
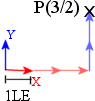
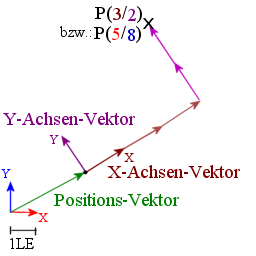
Möchte man in einem einfachen 2D Koordiaten-System den Punkt (X/Y) antragen, so hängt man X mal den Vektor der X-Achse aneinander, und Y mal den Vektor der Y-Achse.
Um die Lage und Größe eines Koordianten System zu beschreiben werden also einmal die Vektoren benötiget die 1 Längen Einheit meiner Achsen beschreiben, sowie ein Vektor der ihre Position in Anhängigkeit zum übergeordneten Koordianten System beschreibt.
Da die Vektoren in OpenGL nicht wie vielleicht vermutet aus 3, sondern aus 4 Teilen bestehen benötigt, haben Vektoren neben X,Y und Z Werten noch einen W-Wert welcher aber weniger zu interessieren hat.
Alle 4 Vektoren sind in jeweils einer Spalte der Matrix enthalten:
| X-Achse | Y-Achse | Z-Achse | Position | |
|---|---|---|---|---|
| X | X | X | X | |
| Y | Y | Y | Y | |
| Z | Z | Z | Z | |
| W | W | W | W |
Folgendes Format könnte man also nutzen, um eine Matrix mit glGetFloatv auszulesen oder mit glLoadMatrix zu setzen.
TVektor = record X,Y,Z,W:glFloat end; TMatrix = array[(mat_XAchse,mat_YAchse,mat_ZAchse,mat_Position)]of TVektor; PMatrix = ^TMatrix;
Berechungen
Anwenden einer Matrix auf einen Vektor/Punkt
Möchte man zum Beispiel wissen wie ein Punkt im übergeordneten Koordianten System aussieht, so kann man dies wie dies zu Berechnen ist kann der obrigen Zeichung entnommen werden(w wird nicht beachtet):
ErgebnisVektor=X*XAchsenVektor + Y*YAchsenVektor + Z*ZAchsenVektor + PositionsVektor
Ausführlich sähe dies dann so aus:
Ergebnis.X=X*XAchse.X + X*YAchse.X + X*ZAchse.X + Position.X; Ergebnis.Y=Y*XAchse.Y + Y*YAchse.Y + Y*ZAchse.Y + Position.Y; Ergebnis.Z=Z*XAchse.Z + Y*YAchse.Z + Y*ZAchse.Z + Position.Z;
Matrizen addieren
Das Addieren von Matrizen ist einfach, wenn man weis wie man Vektoren auf Matrizen anwendet und das in OpenGL Matrizen aus Vektoren bestehen. Man braucht nämlich nur auf alle Spalten/Vektoren einer Matrix die andere Matrix anwenden.
Die Identitätsmatrix
Ist eine Matrix mit folgenden Werten:
| { | 1 | 0 | 0 | 0 | } |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 |
Wendet man auf einen Vektor eine solche Matrix an, so bleibt der Vektor gleich.
Um die aktuelle Matrix zur einer Identitätsmatrix zu machen, ruft man glLoadIdentity auf.
Zugehörige Wertrückgaben
Inhalt einer Matrix:
Aktive Matrix:
- glGet mit GL_MATRIX_MODE
Siehe auch
glMatrixMode, glGet, glLoadIdentity, glLoadMatrix, glTranslate, glRotate, glScale