shader ConeVolumeShadow: Unterschied zwischen den Versionen
(→Geometrie-Crashkurs) |
|||
| Zeile 21: | Zeile 21: | ||
== Voraussetzungen == | == Voraussetzungen == | ||
Aufgrund der besonderen Funktionsweise funktioniert dieser Shader nur dann wenn es sich sämtlichen Objekte in der Szene die einen Schatten werfen sollen um Kugeln handelt. Des weiteren muss innerhalb der Anwendung manuell berechnet werden welche Objekte auf welches Objekt einen Schatten werfen. Je mehr Objekte ein Schatten auf ein einzelnes Objekt werfen, desto langsamer wird das Verfahren. | Aufgrund der besonderen Funktionsweise funktioniert dieser Shader nur dann wenn es sich sämtlichen Objekte in der Szene die einen Schatten werfen sollen um Kugeln handelt. Des weiteren muss innerhalb der Anwendung manuell berechnet werden welche Objekte auf welches Objekt einen Schatten werfen. Je mehr Objekte ein Schatten auf ein einzelnes Objekt werfen, desto langsamer wird das Verfahren. | ||
| + | |||
| + | == Geometrie-Crashkurs == | ||
| + | Um den Shader zu verstehen ist ein wenig Geometrie-Wissen erforderlich, insbesondere bezüglich des Skalarproduktes. Das Skalarprodukt, häufig auch als Dot-Product bezeichnet, ist für zwei 3D-Vektoren <tt>a</tt> und <tt>b</tt> wie folgt definiert: | ||
| + | :<tt>dot(a,b) := a.x*b.x + a.y*b.y + a.z*b.z</tt> | ||
| + | Der Betrag <tt>|a|</tt> eines Vektors <tt>a</tt> ist als dessen Länge bezüglich der euklidischen Norm definiert. Dies ist im wesentlichen der gute alte [http://de.wikipedia.org/wiki/Satz_des_Pythagoras Pythagoras] für drei Dimensionen: | ||
| + | :<tt>|a| := sqrt(a.x*a.x + a.y*a.y + a.z*a.z)</tt> | ||
| + | Eine wichtige Eigenschaft dieses Skalarproduktes ist, dass sich darüber der Winkel <tt>w</tt> zwischen den beiden Vektoren bestimmen lässt. Es gilt: | ||
| + | :<tt>dot(a,b) = |a| * |b| * cos(w)</tt> | ||
| + | Dies wollen wir ausnutzen. In der folgenden Zeichnung sind und die Punkte <tt>A</tt>, <tt>B</tt> und <tt>C</tt> bekannt. Wir wollen <tt>B'</tt> und die Strecke <tt>h</tt> berechnen, also <tt>B</tt> im rechten Winkel auf den Vektor <tt>AC</tt> projizieren. | ||
| + | |||
| + | [[Bild:shader_ConeVolumeProjection.png]] | ||
| + | |||
| + | Mit Hilfe des Skalarproduktes ist dies recht einfach. Zunächst berechnen wir den Vektor <tt>AB := B - A</tt>, sowie den Vektor <tt>AC := C - A</tt>. Letzteren normalisieren wir, indem wir durch die Länge teilen: <tt>n := AC / |AC|</tt>. Da <tt>n</tt> die Länge 1 hat gilt: | ||
| + | :<tt>dot(AB, n) = |AB| * cos(w)</tt> | ||
| + | Aus der Mittelstufe sollte bekannt sein, dass der [http://de.wikipedia.org/wiki/Kosinus#Geometrische_Definition Kosinus wie folgt definiert] ist: | ||
| + | :<tt>cos(w) = Ankathete / Hypotenuse</tt> | ||
| + | Die Hypotenuse ist hier die Strecke <tt>|AB|</tt> und die Ankathete ist die gesuchte Strecke <tt>|AB'| := |B' - A|</tt>. Es gilt also: | ||
| + | :<tt>cos(w) = Ankathete / Hypotenuse</tt> | ||
| + | :<tt><=> cos(w) = |AB'| / |AB|</tt> | ||
| + | :<tt><=> |AB| * cos(w) = |AB'|</tt> | ||
| + | :<tt><=> dot(AB, n) = |AB'|</tt> | ||
| + | Der Punkt <tt>B'</tt> lässt sich nun leicht berechnen, da <tt>n</tt> ja normalisiert war: <tt>B' := n * |AB'|</tt>. Die Strecke <tt>h</tt> folgt aus dem Abstand zwischen <tt>B</tt> und <tt>B'</tt>, also <tt>h := |B - B'|</tt>. | ||
== Funktionsweise == | == Funktionsweise == | ||
Version vom 31. Januar 2010, 12:03 Uhr
Bitte haben Sie etwas Geduld und nehmen Sie keine Änderungen vor, bis der Artikel hochgeladen wurde. |
Inhaltsverzeichnis
Shadername
Zurück zur Shadersammlung
| Beschreibung | Autor | Version |
|---|---|---|
| Kegelvolumen-Schatten | Coolcat | 1.0 |
Bilder
Voraussetzungen
Aufgrund der besonderen Funktionsweise funktioniert dieser Shader nur dann wenn es sich sämtlichen Objekte in der Szene die einen Schatten werfen sollen um Kugeln handelt. Des weiteren muss innerhalb der Anwendung manuell berechnet werden welche Objekte auf welches Objekt einen Schatten werfen. Je mehr Objekte ein Schatten auf ein einzelnes Objekt werfen, desto langsamer wird das Verfahren.
Geometrie-Crashkurs
Um den Shader zu verstehen ist ein wenig Geometrie-Wissen erforderlich, insbesondere bezüglich des Skalarproduktes. Das Skalarprodukt, häufig auch als Dot-Product bezeichnet, ist für zwei 3D-Vektoren a und b wie folgt definiert:
- dot(a,b) := a.x*b.x + a.y*b.y + a.z*b.z
Der Betrag |a| eines Vektors a ist als dessen Länge bezüglich der euklidischen Norm definiert. Dies ist im wesentlichen der gute alte Pythagoras für drei Dimensionen:
- |a| := sqrt(a.x*a.x + a.y*a.y + a.z*a.z)
Eine wichtige Eigenschaft dieses Skalarproduktes ist, dass sich darüber der Winkel w zwischen den beiden Vektoren bestimmen lässt. Es gilt:
- dot(a,b) = |a| * |b| * cos(w)
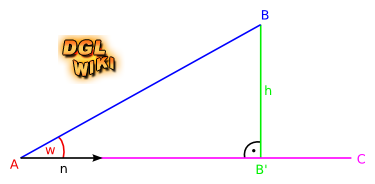
Dies wollen wir ausnutzen. In der folgenden Zeichnung sind und die Punkte A, B und C bekannt. Wir wollen B' und die Strecke h berechnen, also B im rechten Winkel auf den Vektor AC projizieren.
Mit Hilfe des Skalarproduktes ist dies recht einfach. Zunächst berechnen wir den Vektor AB := B - A, sowie den Vektor AC := C - A. Letzteren normalisieren wir, indem wir durch die Länge teilen: n := AC / |AC|. Da n die Länge 1 hat gilt:
- dot(AB, n) = |AB| * cos(w)
Aus der Mittelstufe sollte bekannt sein, dass der Kosinus wie folgt definiert ist:
- cos(w) = Ankathete / Hypotenuse
Die Hypotenuse ist hier die Strecke |AB| und die Ankathete ist die gesuchte Strecke |AB'| := |B' - A|. Es gilt also:
- cos(w) = Ankathete / Hypotenuse
- <=> cos(w) = |AB'| / |AB|
- <=> |AB| * cos(w) = |AB'|
- <=> dot(AB, n) = |AB'|
Der Punkt B' lässt sich nun leicht berechnen, da n ja normalisiert war: B' := n * |AB'|. Die Strecke h folgt aus dem Abstand zwischen B und B', also h := |B - B'|.
Funktionsweise
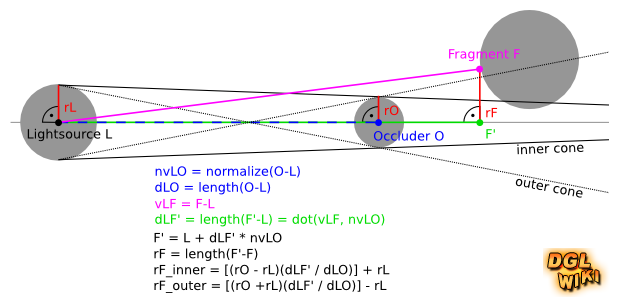
Verwendet man eine gewöhnliche Punktlichtquelle hat das Schatten-Volumen einer Kugel eine sehr einfache Form, nämliche die eines einfachen Kreiskegels. Selbst wenn wir statt der Punktlichtquelle eine Kugellichtquelle verwenden lässt sich das Schattenvolumen noch recht leicht durch zwei Kegel beschreiben. Dies machen wir uns zu nutze.
Code
Vertexshader
Der Vertexshader ist nichts besonderes. Er transformiert einfach nur die Vertexposition sowie die Normale und gibt die Daten weiter. Dieser Shader ist im wesentlichen aus UltimateConquest übernommen. Daher werden hier Vertexattribute und Matrixuniforms selbst definiert. Sofern man noch mit OpenGL 2.x arbeitet kann man aber problemlos die dort verfügbaren eingebauten Uniforms und Attribute benutzen.
uniform mat4 uModelViewProjection;
uniform mat4 uModelView;
uniform mat3 uNormalMatrix;
attribute vec3 aPosition;
attribute vec3 aNormal;
attribute vec2 aTexCoord;
varying vec3 vPosition;
varying vec3 vNormal;
varying vec2 vTexCoord;
void main() {
gl_Position = uModelViewProjection * vec4(aPosition, 1.0);
vPosition = (uModelView * vec4(aPosition, 1.0)).xyz;
vNormal = normalize(uNormalMatrix * aNormal);
vTexCoord = aTexCoord;
}
Fragmentshader
Der Fragmentshader macht den eigentlich Job. Es handelt sich um einen aufgeblasenen Per-Pixel-Light-Shader. Zusätzlich zur normalen Diffuse-Beleuchtung wird in der Funktion shadowFactor() auch noch ein Schattenfaktor berechnet. Diese Funktion berechnet das Produkt sämtlicher Kegelvolumen für das aktuelle Fragment. Am Ende erhalten wir einen Wert zwischen 0.0 und 1.0 der dann einfach mit der Diffuse-Beleuchtung verrechnet wird.
uniform sampler2D uTexture;
// the lightsource described by position and radius
uniform vec4 uLightsource;
vec3 lsPosition = uLightsource.xyz;
float lsRadius = uLightsource.w;
// each shadow volume is described by position (xyz) and radius (w) of the occluder packed into a single vec4
const int shadowMaxCount = 5;
uniform vec4 uShadows[shadowMaxCount];
uniform int uShadowCount;
varying vec3 vPosition;
varying vec3 vNormal;
varying vec2 vTexCoord;
const vec3 cAmbient = vec3(0.025,0.025,0.025);
// simple local diffuse per-pixel lighting
float diffuseFactor() {
vec3 lightDir = normalize(lsPosition-vPosition);
vec3 normal = normalize(vNormal);
return max(dot(lightDir, normal), 0.0);
}
// process all shadow volumes
float shadowFactor() {
float s = 1.0;
// iterate all shadow volumes
for (int i=0; i<uShadowCount; ++i) {
// extract data
vec4 occluder = uShadows[i];
vec3 ocPosition = occluder.xyz;
float ocRadius = occluder.w;
// project fragment (vPosition) on the cone axis => F_
vec3 nvLO = ocPosition - lsPosition;
float dLO = length(nvLO);
nvLO /= dLO;
vec3 vLF = vPosition - lsPosition;
float dLF_ = dot(vLF, nvLO);
if (dLF_ < dLO) {
// fragment before occluder => no shadow
continue;
}
vec3 F_ = lsPosition + dLF_ * nvLO;
float rF = distance(F_, vPosition);
// compute outer and inner radius at F_
float rF_outer = (ocRadius + lsRadius) * (dLF_ / dLO) - lsRadius;
if (rF >= rF_outer) {
// outside the outer cone => no shadow
continue;
}
float rF_inner = (ocRadius - lsRadius) * (dLF_ / dLO) + lsRadius;
if (rF_inner >= rF) {
// inside the inner cone => full shadow
return 0.0;
}
else if (rF_inner >= 0.0 || rF >= -rF_inner) {
// soft shadow, linear interpolation
s *= (rF - rF_inner) / (rF_outer - rF_inner);
}
else {
// light from both sides of the occluder
s *= (-2.0*rF_inner) / (rF_outer - rF_inner);
}
}
return s;
}
void main() {
vec3 texcolor = texture2D(uTexture, vTexCoord).xyz;
gl_FragColor.xyz = cAmbient * texcolor;
float lightFactor = diffuseFactor();
if (lightFactor > 0.004) {
// don't compute shadows for fragments that are already dark from local lighting
lightFactor *= shadowFactor();
}
gl_FragColor.xyz += texcolor * lightFactor;
gl_FragColor.w = 1.0;
}