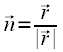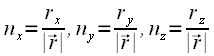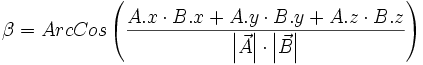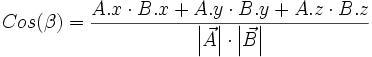Tutorial Lineare Algebra: Unterschied zwischen den Versionen
Flash (Diskussion | Beiträge) K (→Kreuzprodukt (Vektorprodukt = CrossProduct)) |
Flash (Diskussion | Beiträge) K (→Kreuzprodukt (Vektorprodukt = CrossProduct)) |
||
| Zeile 223: | Zeile 223: | ||
===Kreuzprodukt (Vektorprodukt = CrossProduct)=== | ===Kreuzprodukt (Vektorprodukt = CrossProduct)=== | ||
| − | Das Kreuzprodukt ist noch eine Funktion, die man kennen muss. Das Kreuzprodukt nimmt, genau wie das Skalarprodukt, zwei Vektoren entgegen. Als Resultat erhält man beim Kreuzprodukt nicht eine Zahl, sondern einen Vektor. | + | Das Kreuzprodukt ist noch eine Funktion, die man kennen muss. Das Kreuzprodukt nimmt, genau wie das Skalarprodukt, zwei Vektoren entgegen. Als Resultat erhält man beim Kreuzprodukt nicht eine Zahl, sondern einen Vektor. Der Ergebnisvektor hat 2 interessante Eigenschaften. |
| + | # Die Länge des Vectors entspricht dem Flächeninhalt des Parallelograms dass die Ausgangsvektoren aufspannen. Ist der Vector als 3Einheiten lang, ist die Fläche 3Flächeneinheiten groß. | ||
| + | # Für uns noch wichtiger: Der Ergebnisvektor steht ''genau senkrecht'' auf der Fläche die durch die zwei ursprünglichen Vektoren beschrieben wird! Dazu ein Diagram: | ||
[[Bild:Tutorial_lineare_Algebra_CrossArea.gif]] | [[Bild:Tutorial_lineare_Algebra_CrossArea.gif]] | ||
| − | Ich habe hier das Kreuzprodukt des blauen und pinken Vektoren gebildet | + | Ich habe hier das Kreuzprodukt des blauen und pinken Vektoren gebildet. |
<source lang="pascal"> | <source lang="pascal"> | ||
Version vom 25. Juni 2009, 19:52 Uhr
Inhaltsverzeichnis
Vorwort
Hi!
Den Meisten von euch ist sicher schon aufgefallen, dass 90% der 3D Programmierung aus Mathematik besteht. Wie willst du das nächste Doom schreiben, wenn du nicht mal feststellen kannst, ob der Spieler durch eine Wand läuft? Das problematische an der Mathematik ist, dass wenn man nicht von Natur aus eine Interesse dafür hat, erscheint sie oft etwas "trocken". Ich werde mein bestes tun, um mit Hilfe von vielen bunten Diagrammen das Ganze interessant und verständlich zu machen. Seid jedoch gewarnt, dass dies mein erstes Tutorial ist und ich mathematisch viele Sachen vielleicht etwas anders erkläre/mache als "richtig" oder optimal ist.
Ein Haufen praktischer Funktionen
Es gibt ein paar Funktionen, die man können muss, sonst kommt man nicht weit mit OpenGl. Man kann sich natürlich eine 3D Mathe Unit aus dem Internet ziehen, dies ist jedoch, meiner Meinung nach, eine schlechte Idee. Wir sind ja schließlich hier um was zu lernen. Darum lieber eine eigene kleine Unit schreiben, die man richtig versteht. Warum die Funktionen praktisch sind, erkennt man leider erst am Ende, wenn man sie in Kombination gebrauchen kann.
Vektoren
In der Linearen Algebra geht es hauptsächlich um Vektoren. Also brauchen wir ein Vektoren Typ:
type
TVector = record
X,Y,Z : Single; //Dasselbe wie TGLFloat
end;
Wir wollen die Werte nicht einzeln in unseren Vektor eintragen, sondern so:
aVector := MakeVector(1,3,8);
Also brauchen wir Folgendes:
function MakeVector(X,Y,Z : Single) : TVector;
begin
result.x := x;
result.y := y;
result.z := z;
end;
Addition und Subtraktion
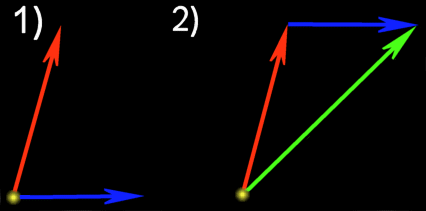
Oben sehen wir zwei Vektoren, die beide im Ursprung (gelber Punkt) anfangen. Das Resultat der Addition wird der grüne Vektor sein. Die zwei Vektoren kannst du dir als zwei separate Anweisungen denken. Die rote "Anweisung" ist gehe 2 Meter Nord; die blaue "Anweisung" ist gehe 1 Meter Ost. Wenn wir die rote "Anweisung" ausführen und die Blaue dazu addieren, d.h. auch ausführen, dann stehen wir sqr(5) Meter (Pythagoras) vom Ursprung entfernt. Das Ganze kann man auch zu einer Anweisung zusammenfassen: der grüne Vektor. Die Addition funktioniert mit alle Vektoren, nicht nur mit denen, die im 90° Winkel zueinander stehen, wie in meinem Nord-Ost Beispiel. Um die Vektoren-Summe zu erhalten, addiert man die Komponente der zwei Vektoren. Genug erklärt, hier ist die Funktion:
function AddVectors(VectorA, VectorB : TVector) : TVector;
begin
{Einfache Vektoraddition}
Result := MakeVector(VectorA.X + VectorB.X,
VectorA.Y + VectorB.Y,
VectorA.Z + VectorB.Z);
end;
Und das Selbe noch für die Subtraktion:
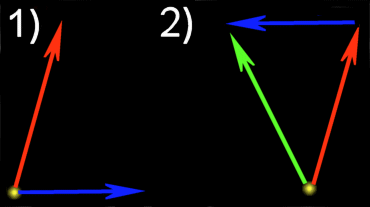
Das Einzige, was an diesem Diagram verwirrend sein mag, ist, dass der blaue Vektor in die "falsche" Richtung zeigt. Das liegt an dem Minus Zeichen in der Subtraktion:
Ein Minus Zeichen dreht einen Vektor um. Wenn die zwei Parameter der Subtraktions-Funktion vertauscht werden, dann erhält man den negativen Vektor. Das lässt sich auch mit einer einfachen Rechnung darstellen:
9 - 4 = 5
4 - 9 = -5
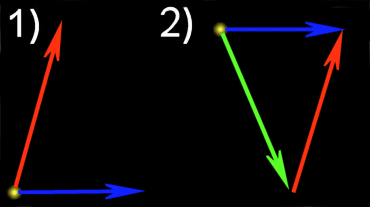
Hätte ich in dem Diagram oben erst den blauen Vektor angegeben wäre Folgendes rausgekommen:
Die Subtraktions-Funktion ist vom Aufbau her, der Additions-Funktion natürlich sehr ähnlich:
function SubVectors(VectorA, VectorB : TVector) : TVector;
begin
{Einfache Vektorsubtraktion}
Result := MakeVector(VectorA.X - VectorB.X,
VectorA.Y - VectorB.Y,
VectorA.Z - VectorB.Z);
end;
Die Länge (Betrag) eines Vektors
Du kennst hoffentlich den Satz des Pythagoras:
Das geht auch in 3D, nur zusätzlich mit der Z-Komponente:
Um nun die Länge (Betrag) zu erhalten, wird wie beim Pythagoras die Seite c im Dreick mit bekannter Formel berechnet:
Und das ganze in Vektorschreibweise:
function Magnitude(Vector : TVector) : Single;
begin
{Gibt die Länge (Betrag) eines Vektors zurück}
result := sqrt(Vector.X * Vector.X+
Vector.Y * Vector.Y+
Vector.Z * Vector.Z);
end;
Es hat sich eingebürgert, dass man die Länge eines Vektoren auch so schreibt: |Vektor|, auch genannt der Betrag eines Vektors. Um es nicht mit dem Absolut Zeichen zu verwechseln, schreiben Manche auch: ||Vektor||.
Einheitsvektoren
Einheitsvektoren sind Vektoren der Länge 1. Es ist leichter, mit Einheitsvektoren zu rechnen, als mit normalen Vektoren, da Multiplikationen mit 1 wegfallen (Siehe Skalarprodukt). Um einen Vektor der Länge 1 zu erhalten, dividieren wir die Komponente des Vektors durch die Länge des Vektors. Der Vektor ist dann "normalisiert".
Die Formel:
Die Länge (von nun an gilt Länge auch für Betrag) des Vektors zu ermitteln ist nun kein Problem mehr, also können wir eine Funktion aufstellen die (fast) jeden beliebigen Vektor normalisiert:
procedure Normalize(var Normal : TVector);
var
Length : Single;
begin
{Der angegebene Vektor wird auf eine Länge (Betrag) von 1 gekürzt,
um dies zu erreichen muss jede Vektorkomponente durch die Länge
(Betrag) des Vektors selbst dividiert werden }
Length := Magnitude(Normal);
if (Length = 0) then Length := 1;//Wir wollen keine Division durch 0
Normal.X := Normal.X / Length;
Normal.Y := Normal.Y / Length;
Normal.Z := Normal.Z / Length;
end;
Das Einzige, was hier unerwartet sein mag, ist die "if" Abfrage. Wenn der Vektor (0,0,0) ist, würde die Länge 0 sein und somit einen "Division by Zero" Fehler erzeugen. Falls die Länge 0 ist, dividieren wir deshalb durch 1.
Manchmal ist es nötig, einen Vektor um einen Faktor zu verlängern. Um dies zu erreichen, wird jede Komponente des Vektors mit dem Faktor multipliziert:
function ScaleVector(Vector : TVector; Multi : Single) : TVector;
begin
{ Der Vektor wird skaliert mit dem angegeben Faktor Multi }
{ Dies ändert nicht die Richtung des Vektors! }
result.x := Vector.x * Multi;
result.y := Vector.y * Multi;
result.z := Vector.z * Multi;
end;
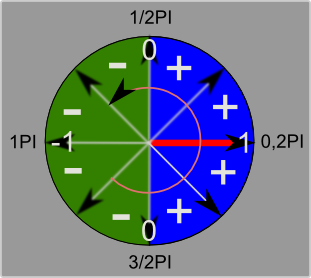
Bogenmaß und Gradmaß
Wenn du in OpenGl (und auch sonst bei PCs) irgendwo einen Winkel siehst, kannst du fast davon ausgehen, dass er im Bogenmaß (Radians) angegeben wird. Sollten es wirklich Grad sein, steht das meistens groß daneben [Amk: Bitte Überprüfen: siehe glRotate ]. Die trigonometrischen Funktionen in Delphi sind übrigens auch alle auf Bogenmaß ausgelegt. Gradmaß(deg) und Bogenmaß(rad) kann man leicht umrechnen:
Diese Umrechnung ist hier wirklich nur als Hilfe gedacht. Rechnet bitte nicht in euren OpenGl Programmen alles nach Grad um und später wieder zurück nach Bogenmaß. Wenn du es ernst meinst, mit der 3D Programmierung, dann lern gleich mit dem Bogenmaß umzugehen.
Skalarprodukt (Punktprodukt = DotProduct)
Das Skalarprodukt ist eine der meistgebrauchten Funktionen - und das aus gutem Grund: Wenn es irgendwie um einen Winkel in einer Berechnung geht, ist wahrscheinlich das Skalarprodukt mit drin:
wobei ![]() für den Kosinus-Winkel (in Rad) zwischen den Vektoren
für den Kosinus-Winkel (in Rad) zwischen den Vektoren ![]() und
und ![]() steht.
steht.
Diese Formel ist noch nicht brauchbar, da zwei der Variablen unbekannt sind, nämlich das Skalarprodukt und der Winkel (im weiteren ![]() [sprich: betta] genannt).
[sprich: betta] genannt).
Bemerkung: Wenn beide Vektoren Einheitsvektoren sind, dann ist das Skalarprodukt gleich dem Kosinus des Zwischenwinkels ![]() , d.h. wenn
, d.h. wenn ![]() und
und ![]() dann folgt daraus
dann folgt daraus ![]() und damit ist dies der Kosinus von
und damit ist dies der Kosinus von ![]() (
(![]() in Rad) des oben gezeigten Zwischenwinkels. Zur Erinnerung der Kosinus kann immer nur Werte zwischen -1 und 1 annehmen, und in diesem Fall würde das Skalarprodukt ebenfalls nur Werte zwischen -1 und 1 annehmen.
in Rad) des oben gezeigten Zwischenwinkels. Zur Erinnerung der Kosinus kann immer nur Werte zwischen -1 und 1 annehmen, und in diesem Fall würde das Skalarprodukt ebenfalls nur Werte zwischen -1 und 1 annehmen.
Um eine Vorstellung zwischen den verschieden Kosinus/Sinus/Tangens-Gradvarianten (DEG, RAD, GRAD) zu erhalten hilft hier vielleicht die folgende Darstellung als Pascal Code (hier beispielhaft nur der Kosinus, gilt aber genauso für Sinus,Tanges und Cotanges):
type TDeg = Double;
type TRad = Double;
type TGra = Double;
// der Kosinus rechnet einen vollen Kreis mit Werten von 0 - 360
function cos(Value: TDeg): Double;
// der Kosinus rechnet einen vollen Kreis mit Werten von 0 - 2PI
function cos(Value: TRad): Double;
// der Kosinus rechnet einen vollen Kreis mit Werten von 0 - 400
function cos(Value: TGra): Double;
Doch jetzt weiter im Text, das Problem mit den zwei unbekannten Variablen hat zum Glück jemand für uns gelöst:
Wenn wir die zwei Gleichungen gleichsetzen, erhalten wir folgendes:
Sehr schön. Damit können wir etwas anfangen: Wir können mit ein paar einfachen Rechnungen an den Winkel zwischen den zwei Vektoren kommen.
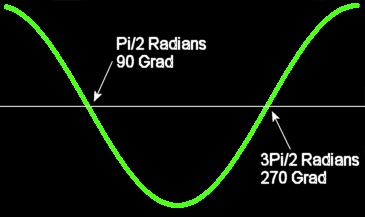
Aus Performance Gründen sollte dies möglichst vermieden werden, da die ArcCos Funktion langsam ist. Auch um dies Problem gibt es (teilweise) eine schlaue Lösung. Lassen wir das mit dem ArcCos weg und schauen uns den Kosinus Graphen an:
Falls der Winkel Pi/2 oder 3Pi/2 ist, wird der Kosinus 0 sein. Andersrum gedacht: Wenn der Kosinus 0 ist dann ist der Winkel Pi/2 oder 3Pi/2. Wenn Cos(ß) zwischen Pi/2 und 3Pi/2 liegt, ist das Vorzeichen von Cos(ß) negativ. Am Graphen solltest du auch sehen können das beim Rest das Vorzeichen positiv ist. Und das Ganze noch mal graphisch: (Der Rote Vektor ist der "Hauptvektor")
Wir werden das Skalarprodukt so ausrechnen:
function DotProduct(VectorA,VectorB : TVector) : Single;
begin
{Das Ergebnis des Punktprodukts ist der Kosinus des Winkels
zwischen den beiden Vektoren, wenn Vektor A und Vektor B normalisiert
wurden, ansonsten muss man das Punktprodukt noch durch die Längen
der Vektoren teilen.
Ist der Kosinus positiv, dann ist der Winkel kleiner 90°, ist der
Kosinus negativ dann ist der Winkel größer 90°. Benutze den ArcusKosinus
um den Winkel aus den Werten zwischen -1 und 1 wieder in Grad-Bogenmaß
(Rad) zu erhalten. }
result := VectorA.X*VectorB.X+
VectorA.Y*VectorB.Y+
VectorA.Z*VectorB.Z;
end;
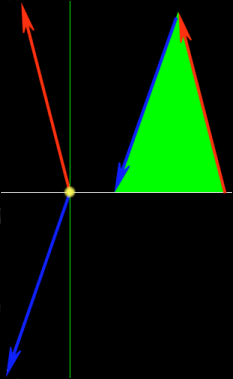
Kreuzprodukt (Vektorprodukt = CrossProduct)
Das Kreuzprodukt ist noch eine Funktion, die man kennen muss. Das Kreuzprodukt nimmt, genau wie das Skalarprodukt, zwei Vektoren entgegen. Als Resultat erhält man beim Kreuzprodukt nicht eine Zahl, sondern einen Vektor. Der Ergebnisvektor hat 2 interessante Eigenschaften.
- Die Länge des Vectors entspricht dem Flächeninhalt des Parallelograms dass die Ausgangsvektoren aufspannen. Ist der Vector als 3Einheiten lang, ist die Fläche 3Flächeneinheiten groß.
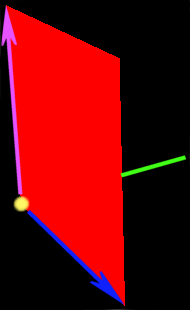
- Für uns noch wichtiger: Der Ergebnisvektor steht genau senkrecht auf der Fläche die durch die zwei ursprünglichen Vektoren beschrieben wird! Dazu ein Diagram:
Ich habe hier das Kreuzprodukt des blauen und pinken Vektoren gebildet.
function CrossProduct(VectorA,VectorB : TVector) : TVector;
begin
{Erzeugt einen Vektor der senkrecht zur Fläche ist,
die durch die zwei gegeben Vektoren erzeugt wurde }
Result.X := VectorA.Y*VectorB.Z - VectorA.Z*VectorB.Y;
Result.Y := VectorA.Z*VectorB.X - VectorA.X*VectorB.Z;
Result.Z := VectorA.X*VectorB.Y - VectorA.Y*VectorB.X;
end;
Die Reihenfolge in der man die Vektoren der Kreuzprodukt Funktion überreicht ist wichtig. Wenn ich in dem vorigen Diagram erst den pinken Vektor überreicht hätte wäre Folgendes rausgekommen:
Auf diesem Diagram ist genau die selbe Fläche zu sehen wie auf dem vorigen, nur aus einem anderen Blickwinkel, damit man den Vektor überhaupt sehen kann. Der Vektor, den wir zurück bekommen, hat genau die selbe Länge wie der Vorige, er zeigt jedoch in die gegengesetzte Richtung. Er ist also das Negativ des vorigen Vektors. Negative Vektoren wurde schon in "Addition und Subtraktion" besprochen.
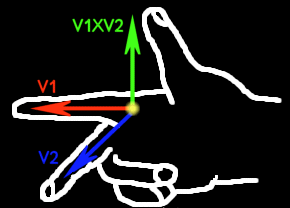
Es gibt eine Methode, sich zu merken, in welche Richtung das Resultat zeigen wird: Wenn du deine rechte Hand ausstreckst, gilt Folgendes: Der Zeigefinger ist der erste Vektor, der Mittelfinger der Zweite und der Daumen das Resultat. Graphisch:
Das nennt man die Rechte-Hand-Regel. Ich hoffe, dass du in dem Bild eine rechte Hand erkennen kannst ;-)
Alles was normal ist
Zum Abschluss will euch eine Funktion zeigen, die die Normale eines beliebigen Dreiecks finden kann. Dazu müssen wir erst Dreiecke speichern können:
type
TTriangle = array[0..2] of TVector;
Um die Normale zu finden benötigen wir zwei Vektoren. Wir haben nur die drei Punkte des Dreiecks. Durch Subtraktion kann man aus den drei Punkten zwei Vektoren bilden:
Ich hoffe das du den Zusammenhang zwischen den zwei roten bzw. blauen Vektoren sehen kannst. Wenn nicht schau dir die Vektoren Subtraktion bitte noch mal genau an. Wir gebrauchen das Kreuzprodukt um einen Vektor zu finden der senkrecht auf diesen zweien steht. Zum Schluss wird dieser normalisiert.
function GetNormal(Triangle : TTriangle) : TVector;
var
VectorA, VectorB, Normal : TVector;
begin
{To get the normal we first need to define a plane.
To do this we use the three vertices to create two
vectors, thereby defining a plane. If we give these
two vectors to the CrossProduct function we get a
vector that is perpendicular to the plane in return.
All we then need to do is cut this vector to a length
of 1 and we have our normal.}
{ Um die Normale zu erhalten müssen wir als erstes
eine Fläche festlegen. Um dies zu erreichen benutzen
wir die drei Eckpunkte um zwei Vektoren zu erhalten.
Wenn wir diese Vektoren der Punktprodukt Funktion
übergeben, bekommen wir einen Vektor zurück der
Senkrecht zur Fläche ist. Alles was wir dann noch
machen müssen ist den Vektor auf eine Länge von 1
zu kürzen und wir erhalten unseren Nomalenvektor. }
VectorA := SubVectors(Triangle[0],Triangle[1]);
VectorB := SubVectors(Triangle[1],Triangle[2]);
Normal := CrossProduct(VectorA,VectorB);
Normalize(Normal);
result := Normal;
end;
Wenn alles glatt läuft, haben wir die Normale des Dreiecks.
Nachwort
Ich hoffe dieses Tutorial hat dem ein oder anderen was gebracht. Ich habe auf jeden Fall eine Menge gelernt durch das Schreiben. Ist irgendwie immer im Leben so. Sobald man etwas erklären möchte, muss man das erst selber konkret durchdenken...
Vielen dank an Delphic für die sprachliche Hilfe (War sehr nötig).
|
|
||
Vorhergehendes Tutorial: - |
Nächstes Tutorial: Tutorial Nachsitzen |
|
|
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen. |
||