Mesh: Unterschied zwischen den Versionen
(Eigenschaften: 2-Mannigfaltigkeit, Geschlossenheit) |
(→Euler-Formel) |
||
| Zeile 19: | Zeile 19: | ||
Ein Mesh ist ''2-mannigfaltig'', wenn die folgenden Eigenschaften gegeben sind. | Ein Mesh ist ''2-mannigfaltig'', wenn die folgenden Eigenschaften gegeben sind. | ||
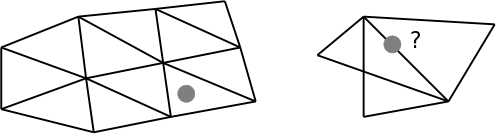
* ''Local Disc Property'': Um jeden beliebigen Punkt auf dem Mesh lässt sich immer eine ε-Umgebung (= Kugel mit Radius ε > 0) finden, so dass die Schnittmenge aus ε-Umgebung und Mesh [http://de.wikipedia.org/wiki/Hom%C3%B6omorph homöomorph] (nicht verwechseln mit ''homomorph'') zu einer planaren Scheibe ist. Sofern es sich um einen Punkt auf dem Rand handelt, kann die Schnittmenge auch homöomorph zu einem Halbkreis sein. | * ''Local Disc Property'': Um jeden beliebigen Punkt auf dem Mesh lässt sich immer eine ε-Umgebung (= Kugel mit Radius ε > 0) finden, so dass die Schnittmenge aus ε-Umgebung und Mesh [http://de.wikipedia.org/wiki/Hom%C3%B6omorph homöomorph] (nicht verwechseln mit ''homomorph'') zu einer planaren Scheibe ist. Sofern es sich um einen Punkt auf dem Rand handelt, kann die Schnittmenge auch homöomorph zu einem Halbkreis sein. | ||
| + | : [[Bild:2manfold-localdisc.png]] | ||
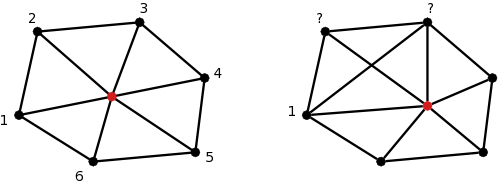
* ''Edge Ordering Property'': Die Nachbarvertices eines jeden Vertex lassen sich eindeutig im Uhrzeigersinn aufzählen. | * ''Edge Ordering Property'': Die Nachbarvertices eines jeden Vertex lassen sich eindeutig im Uhrzeigersinn aufzählen. | ||
| + | : [[Bild:2manfold-edgeorder.png]] | ||
* ''Face Count Property'': Jede innere Kante hat genau zwei adjazente Faces. Jede Kante die am Rand liegt hat genau ein adjazentes Face. | * ''Face Count Property'': Jede innere Kante hat genau zwei adjazente Faces. Jede Kante die am Rand liegt hat genau ein adjazentes Face. | ||
====Geschlossenheit==== | ====Geschlossenheit==== | ||
Ein Mesh heißt geschlossen, wenn es keinen Rand besitzt. Insbesondere besitzt das Mesh also ein "innen" und ein "außen". Ist das Mesh gleichzeitig auch 2-mannigfaltig, besitzt jede Kante genau zwei adjazente Faces. | Ein Mesh heißt geschlossen, wenn es keinen Rand besitzt. Insbesondere besitzt das Mesh also ein "innen" und ein "außen". Ist das Mesh gleichzeitig auch 2-mannigfaltig, besitzt jede Kante genau zwei adjazente Faces. | ||
| + | |||
| + | ====Euler-Formel==== | ||
| + | Für ''geschlossene'' und ''2-mannigfaltige'' Meshes gilt die Euler-Formel: | ||
| + | : <tt>V - E + F = 2(1-g)</tt> | ||
| + | Die Variablen {{INLINE_CODE|V}}, {{INLINE_CODE|E}} und {{INLINE_CODE|F}} stehen dabei für die Anzahl der Vertices, Kanten (Edges) und Faces. Die Variable {{INLINE_CODE|g}} steht für den Genus des Objektes. Intuitiv ist der Genus eines Meshes die Anzahl der "Griffe". (Ein Bild wäre wohl hilfreich, das kommt noch) | ||
| + | |||
| + | Sofern das Mesh nicht ''geschlossen'' ist, rechnet man einfach mit einem zusätzlichen Face, welches das Mesh schließt. | ||
Version vom 4. April 2009, 12:24 Uhr
Als Mesh (engl. für Netz) bezeichnet man die Menge an Vertices, welche ein Objekt formen. Die Vertices bilden zusammen eine Art Gitter oder Netz, welches die Oberfläche des Objektes abbildet. (siehe auch: Primitive)
 Eine beleuchtete (siehe glLight) Kugel. |
 Die selbe Kugel in der Gitternetz Darstellung (siehe glPolygonMode). Das Gitternetz entspricht dem Mesh. |
Wenn man davon spricht, dass ein Objekt aus verschiedenen Meshes besteht, dann heißt dies, dass das Objekt aus verschiedenen Teilobjekten zusammen gesetzt ist. In vielen Modellformaten (z.B. 3ds, das Format von 3D Studio Max) werden alle Vertices eines Geometrieobjektes (das sind die Basisobjekte die 3D Studio Max anbietet. Z.B. Würfel, Kugel, etc.) einem Mesh zu geordnet. Besteht z.B. eine Figur aus den Einzelobjekten Kopf, Rumpf, Arm-Links, Arm-Rechts, Bein-Links, Bein-Rechts, so sind diese Einzelobjekte jeweils als ein Mesh in der 3ds Datei gespeichert. Jedes Mesh besteht dann wiederum aus vielen Vertices, die das oben genannte Gitter bilden.
Inhaltsverzeichnis
Eigenschaften
Ein Mesh kann diverse Eigenschaften haben. Aus diesen Eigenschaften lassen sich lassen sich Aussagen über das Verhältnis zwischen Vertices, Kanten (Edges) und Faces treffen.
2-Mannigfaltigkeit
2-Mannigfaltigkeit ist eine wichtige Eigenschaft. Einfach ausgedrückt ist sie gegeben, wenn das Mesh aus einer einfachen Oberfläche besteht an der keine zusätzlichen Teile angebracht sind. Eine etwas formalere Definition folgt nun. Eine alternative Definition findet sich bei Wikipedia.
Ein Mesh ist 2-mannigfaltig, wenn die folgenden Eigenschaften gegeben sind.
- Local Disc Property: Um jeden beliebigen Punkt auf dem Mesh lässt sich immer eine ε-Umgebung (= Kugel mit Radius ε > 0) finden, so dass die Schnittmenge aus ε-Umgebung und Mesh homöomorph (nicht verwechseln mit homomorph) zu einer planaren Scheibe ist. Sofern es sich um einen Punkt auf dem Rand handelt, kann die Schnittmenge auch homöomorph zu einem Halbkreis sein.
- Edge Ordering Property: Die Nachbarvertices eines jeden Vertex lassen sich eindeutig im Uhrzeigersinn aufzählen.
- Face Count Property: Jede innere Kante hat genau zwei adjazente Faces. Jede Kante die am Rand liegt hat genau ein adjazentes Face.
Geschlossenheit
Ein Mesh heißt geschlossen, wenn es keinen Rand besitzt. Insbesondere besitzt das Mesh also ein "innen" und ein "außen". Ist das Mesh gleichzeitig auch 2-mannigfaltig, besitzt jede Kante genau zwei adjazente Faces.
Euler-Formel
Für geschlossene und 2-mannigfaltige Meshes gilt die Euler-Formel:
- V - E + F = 2(1-g)
Die Variablen V, E und F stehen dabei für die Anzahl der Vertices, Kanten (Edges) und Faces. Die Variable g steht für den Genus des Objektes. Intuitiv ist der Genus eines Meshes die Anzahl der "Griffe". (Ein Bild wäre wohl hilfreich, das kommt noch)
Sofern das Mesh nicht geschlossen ist, rechnet man einfach mit einem zusätzlichen Face, welches das Mesh schließt.