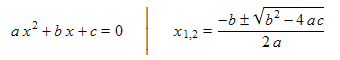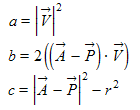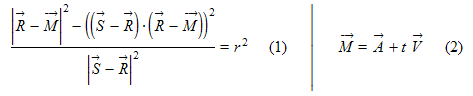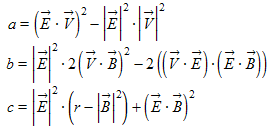Version vom 9. April 2008, 13:01 Uhr

Treffpunkt Kugel - Polygon

Grundsätzliches

Worum geht es in diesem Tutorial?

Hier nun der zweite Teil des Kollisions-Tutorials. Während der erste Teil eher eine lockere Plauderei über Kollisionen war, befassen wir uns nun ausführlich mit einer sehr wichtigen Art der Kollision. Am besten mache ich es deutlich, indem ich die Szenerie beschreibe. Wir haben eine Landschaft, gebildet aus dreieckigen Polygonen, die ihrerseits aus einer Heightmap berechnet wurden. In der Landschaft stehen verschiedene, aufgesetzte Objekte wie Gebäude, Brücken oder Bäume. Ein Objekt bewegt sich auf dem Gelände und bemüht sich, von gelegentlichen Sprüngen abgesehen, um Bodenhaftung - es passt seine Bewegungen dem Gelände an oder ändert die Richtung, wenn es irgendwo anstößt.

In diesem Tutorial möchte ich ein Verfahren beschreiben, wie wir die allgegenwärtige Kollision mit dem Gelände oder die gelegentliche Kollision mit weiteren Objekten feststellen und das bewegte Objekt in eine geeignete Richtung weisen können. Ich werde also sowohl auf die Kollisionserkennung als auch auf die Kollisionsverarbeitung eingehen, wobei sich die Verarbeitung auf die Berechnung des Gleitpfades über den Boden oder entlang des Hindernisses beschränkt. Zwar wird es nicht immer sinnvoll sein, das Objekt auf den Gleitpfad zu bringen, z.B. bei "Frontalkollisionen", aber das sind Überlegungen, die von der jeweiligen Situation abhängen und für die es keine allgemeingültigen Lösungen gibt.

Das Tutorial besteht aus drei Abschnitten. Im diesem ersten Abschnitt spreche ich einige allgemeine Probleme an, während ich im zweiten Abschnitt den Algorithmus vorstellen werde, ohne jedoch auf jede einzelne Funktion einzugehen. Die bringe ich in einem besonderen Beitrag, und zwar in Form einer Werkzeugkiste. Für diese etwas eigenwillige Gliederung gibt es einen Grund. Viele Wege führen bekanntlich nach Rom, und das gilt auch für die Algorithmen. Das Verfahren, das ich vorstelle, ist nur einer von mehreren möglichen Wegen - vielleicht nicht einmal der beste. Mein Wunsch ist es, dass ihr nicht einfach den Code abkupfert, sondern euch selber mit der Sache auseinandersetzt und nach eigenen Wegen oder Verbesserungen sucht. Dabei kann die Werkzeugkiste hilfreich sein.

Warum eine Kugel?

In Wirklichkeit geht es gar nicht um die Kugel an sich wie beim Billardtisch im 1. Teil des Tutorials, sondern es geht um Objekte, die annähernd mit der Form einer Kugel beschrieben werden können. Betrachten wir mal zwei Akteure aus Tuxracer:

Links Tux, der uns freundlicherweise fast immer das Hinterteil zeigt, rechts Boris, der es etwas lockerer angeht

Klar, dass auch ein mit Heringen vollgefressener Pinguin trotz enormen Taillenumfangs niemals zu einer richtigen Kugel wird, aber wenn es um Kollisionen geht, muss es nicht unbedingt stören, wenn der Anzug nicht ganz genau passt ...

Trotzdem müssen wir nicht alles in eine Kugel pressen. Nehmen wir als Beispiel den Menschen mit seinem aufrechten Gang und seiner (meist) länglichen Gestalt. Der hätte verständlicherweise etwas dagegen, den Kopf zwischen die Knie zu klemmen und in der Hocke durch die Gegend zu hopsen. Da hilft uns u.U. das Ellipsoid weiter. Das Ellipsoid ist so etwas wie der dreidimensionale Verwandte der Ellipse und natürlich viel anpassungsfähiger. Ich werde in diesem Tutorial noch nicht näher darauf eingehen, das ist Thema des 3. Teils. Aber eines sollte ich erwähnen: Auch bei Verwendung des Ellipsoids wird die Kollision mit der Kugel berechnet, denn die Umrechnung erfolgt außerhalb des eigentlichen Algorithmus.

Auf die Verpackung kommt es an

Dann gibt es ja noch das Schneemann-Prinzip, bei dem wir eine Form mit mehreren Kugeln umhüllen. Die Kollisionserkennung muss dann mit allen Kugeln durchgeführt werden. Das ist aber nur ein Gedankenanstoß, wer möchte, kann den Faden ja weiter spinnen. Halten wir jetzt nur fest, dass die Kugel dominiert, egal wie wir unser Männeken einpacken. Also werden wir uns ganz auf die Kugel konzentrieren.

Womit kollidiert die Kugel?

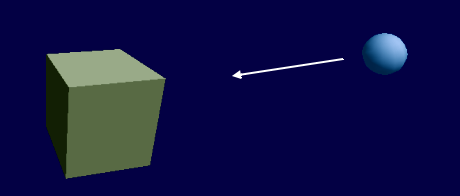
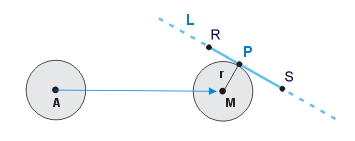
Schauen wir uns einmal an, wie das Aufeinanderprallen von Kugel und Polygon vonstatten gehen kann, und was zu tun ist, damit das Treffen wunschgemäß abläuft.

Die Kugel wird auf den Würfel prallen, genauer: auf eines der 6 Polygone. In diesem Fall sind es Quadrate. Dass nur drei der Flächen in Frage kommen, können wir im Bild zwar sofort erkennen, aber diese Übersicht können wir unserem Programm schwerlich beibringen. Wir prüfen also alle 6 Polygone oder sogar 12, wenn wir Dreiecke anstatt der Quadrate verwendet haben. Wo genau die Kugel kollidiert, ist dem Bild nicht zu entnehmen. Aber etwas anderes sehen wir hoffentlich. Es muss ja gar nicht sein, dass die Kugel auf eine Fläche trifft. Ebenso ist möglich, dass nur eine der Kanten getroffen wird - oder die Ecke. Und damit haben wir die drei Fälle, die wir untersuchen müssen:

• Kollision an der Fläche des Polygons
• Kollision an einer Kanten des Polygons
• Kollision an einer Ecken des Polygons

Dass die 6 Quadrate einen Würfel bilden, ist für die Kollisionsberechnung uninteressant; alles ist in Polygonen organisiert (in diesem Fall Quads, um mit OpenGL zu sprechen). Um das Gebilde auf Kollisionen zu prüfen, müssen wir uns demnach 6 Polygone mit jeweils 1 Fläche, 4 Kanten und 4 Ecken vornehmen. Dass dabei jede Kante und Ecke mehrfach vorkommt, könnte ein Anlass sein, über Optimierung nachzudenken. Aber das lasse ich mal aus, wer möchte, kann sich ja damit befassen.

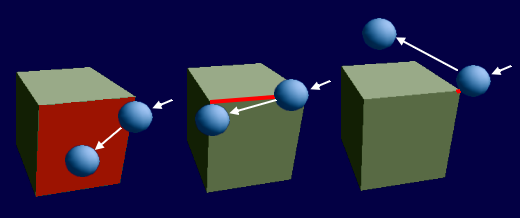
Wie wirkt sich nun die Kollision an den drei Dingen aus? Eingangs sprach ich von einem Gleitpfad, der nicht immer, aber doch meistens der richtige Weg aus dem Kollisionsbereich ist. Betrachten wir die Fälle wieder in einer Abbildung:

Kollision mit der Fläche - Kante - Ecke

Wenn die Kugeloberfläche eine Polygonfläche berührt, ist der Fall ziemlich klar. Die Kugel wird an der Polygonfläche entlanggleiten, das ist dann zugleich die Gleitebene. Anders bei einer Kollision an der Kante. Hier hängt die weitere Bewegungsrichtung davon ab, wie die Kante angeschnitten wird. Der zu konstruierende Gleitpfad erfolgt an einer fiktiven Gleitebene und führt mehr oder weniger von der Kante weg. Ähnliches gilt für die Kollision an der Ecke. Hierbei kann die Kugel irgendwohin umgeleitet werden, selbstverständlich nicht beliebig, denn wiederum spielt der Anschnitt eine Rolle.

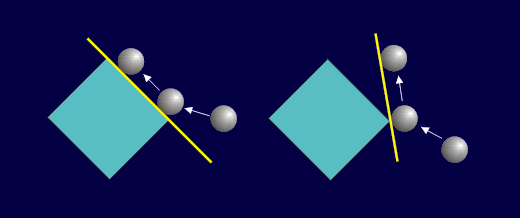
In der zweidimensionalen Darstellung werden die Verhältnisse noch etwas deutlicher sichtbar. Die gelbe Linie kennzeichnet die Gleitebene.

Die Gleitebene. Mal geht es am Hindernis entlang, mal entfernt sich die Kugel vom Hindernis

Probleme: Kollsisionslücken und Kollisionsfallen

Ich glaube, jeder, der sich etwas intensiver mit Kollisionen befasst, kennt und fürchtet die folgende Situation. Da scheint alles prächtig zu funktionieren, dann geht man hin, dreht ein Haus um 30° und steuert die Kante mit der Kugel an. Doch anstatt vorschriftsmäßig abzuprallen, spielt die Kugel "Durch-die-Wand-gehen" und betritt das Haus, ohne die Tür zu benutzen. Zum Glück kann sie auf der anderen Seite wieder hinaus, denn vorsorglich haben wie die Rückseiten der Polygonflächen von der Kollision ausgeschlossen. Dann geht es auf das nächste Haus zu. Nun spielt die Kugel auf andere Weise verrückt, denn sie bleibt wie eine Klette an der Hauswand kleben und rührt sich nicht mehr vom Fleck.

Zwei verschiedene Erscheinungsformen des Fehlverhaltens der Kugel. Ich nenne sie Kollisionslücken (durch das Hindernis) und Kollisionsfallen (am Hindernis kleben). Beide Störungen haben gemeinsam, dass sie kaum reproduzierbar sind. Es kann einige Dutzend mal gut gehen, und dann - rrrums, passiert es wieder. Gut, wenn wir in solchen Fällen das Programm nicht sofort beenden, sondern mit der Kamera dicht heranfahren können, um die "Kontaktstellen" zu prüfen. Aber mehr als eine vage Spur erhalten wir dabei nicht. Etwas informativer sind da schon Protokolldateien, die alle Vektoren zum Zeitpunkt der Kollision auflisten. Doch das setzt wiederum voraus, dass die Störung wenigstens halbwegs zu reproduzieren ist, damit wir gezielt an die gewünschten Daten gelangen könnnen. Alles in allem also keine erfreuliche Sache.

Bei meinen Versuchen konnte ich feststellen, dass solche Kollisionslücken und -fallen eher selten durch einen Fehler in einer mathematischen Funktion entstehen oder auf eine fehlgeschlagene Kollisionserkennung zurückzuführen sind. Im Gegenteil: Gerade in solchen Fällen häufen sich die Kollisionen in auffälliger Weise, und fast immer erfolgt dabei die erste Kollision an einer Kante. Dabei spielt der Winkel, mit der die Kante angeschnitten wird, ebenso eine Rolle wie die Länge des Bewegungsschrittes. Letzteres scheint unlogisch zu sein, erklärt aber das unregelmäßige Auftreten von Kollisionslücken auch dann, wenn die Kugel sich auf einer exakten und reproduzierbaren Bahn bewegt.

Vieles spricht dafür, dass nicht zuletzt der Gleitpfad verantwortlich ist. Der wird zwar richtig berechnet, führt die Kugel aber an eine Stelle, mit der nachfolgenden Kollisionen u.U. nichts Vernünfiges anfangen können, oft tief im Schnittbereich einer Ebene. Entweder flutscht die Kugel bei den Folgekollisionen durch oder sie gerät in eine rekursive Dauerkollision und bleibt stecken. Damit solche Fehler nicht auftreten, muss insbesondere das Zusammenspiel von Kollisionserkennung und Gleitpfadberechnung stimmen. Aber selbst wenn wir feststellen, dass anscheinend alles reibungslos verläuft, bleibt immer ein gewisser Unsicherheitsfaktor. Ich denke, das gilt auch für den folgenden Algorithmus, obwohl ich damit noch keine Lücke oder Falle ausmachen konnte. Bisher jedenfalls, doch vielleicht sind die Leser dieses Tutorials erfogreicher ;-)

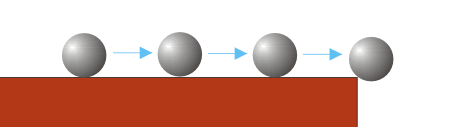
Zum Schluß noch ein kleines Beispiel, wie eine Kollisionsfalle aussehen kann. Eine Kugel rollt über einen Kasten und sollte eigentlich über die Kante hinweg abrollen. Stattdessen bleibt sie stehen, als hätte sie Angst, in die Tiefe zu springen.

Wie festgeklebt an der Kante

Es "gelang" mir nur ein einziges Mal, die Kugel in diese bizarre Endlage zu bringen. Leider ist einmal bereits einmal zu viel, und ich sah mich veranlasst, die Kantenkollsion komplett zu überprüfen.

Der Algorithmus

Vorselektion und Berechnung des Schnittbereiches

Dieser Vorbereitungsschritt erfüllt zwei Aufgaben. Zum einen sollen so früh wie möglich alle Situationen ausgeschlossen werden, bei denen keine Kollision stattfinden kann. Denn bei aller "Kontaktfreudigkeit": die beste Kollision ist immer noch die nicht stattfindende, denn sie erspart dem Rechner viel Arbeit.

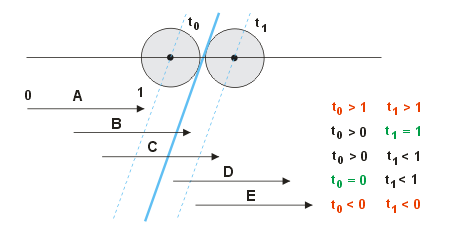
Die andere Aufgabe besteht darin, den Schnittbereich der Kugel mit der Polygonebene zu berechnen - für spätere Rechnungen. Der Schnittbereich hängt vom Radius der Kugel ab und geht von der ersten Berührung mit der Vorderseite der Ebene bis zu der Stelle, wo sich die Kugel auf der Rückseite von der Ebene löst. Wenn die Kugel innerhalb eines Bewegungsschrittes die Ebene voll durchdringt, ist der Schnittbereich ein Abschnitt des Bewegungsvektors, der wiederum durch die Werte 0 und 1 begrenzt wird (siehe Werkzeugkiste). Aber das ist nur ein Sonderfall. Die Zeichnung zeigt die möglichen Fälle:

A und E. Sowohl t0 als auch t1 liegen außerhalb des Intervalls [0, 1], so dass keine Kollision stattfinden kann.

B. Der Bewegungsschritt führt in den Schnittbereich hinein, so dass t1 > 1 ist. Hier muss t1 auf den Wert 1 begrenzt werden. Was darüber hinaus geht, ist zu weit für eine Kollision.

C. Das ist der oben beschriebene Fall.

D. Nun befindet sich die Kugel schon vor der Bewegung im Schnittbereich. Logischerweise wird jetzt t0 begrenzt, d.h. auf 0 gesetzt. Im Minusbereich gibt es keine Kollision.

Wozu benötigen wir nun t0 und t1? Ganz einfach, wir berechnen den Kollisionspunkt (Intersektionspunkt) und prüfen nach, ob sich dieser innerhalb des Schnittbereichs befindet. Falls ja, merken wir uns die Distanz bis zum Kollionspunkt und prüfen die anderen Ecken und Kanten in gleicher Weise. Dabei benutzen wir t1 als fließende, hintere Grenze. Wenn wir eine Kollision irgendwo zwischen t0 und t1 feststellen, dann stellen wir t1 auf den Kollisionspunkt und sorgen auf diese Weise dafür, dass die nächste Kollision schon näher stattfinden muss, wenn sie erkannt werden will. Die nächstliegende Kollision bleibt am Schluss übrig und muss sich nach Verlassen der Funktion mit denen anderer Polygone messen. Sieger ist schließlich das Polygon mit dem kleinsten Schritt zum Intersektionspunkt.

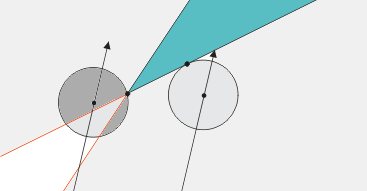
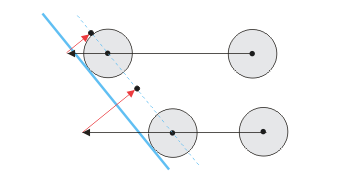
Im übrigen ist t1 bei Flächenkollisionen ohne Bedeutung, denn die Kugel kann nur in t0 mit der Ebene kollidieren. Anders bei Kanten und Ecken; hierbei erfolgt die Berührung normalerweise, wenn die Kugel schon in die Ebene eingedrungen ist.

Gravierende Unterschiede zwischen Kanten- und Flächenkollision

Rechts die Kugel, die mit der Fläche kollidiert. Sie ist noch nicht in die Ebene eingedrungen, während die linke Kugel beim Erreichen der Kante gleich zwei Ebenen schneidet, eine sogar über den Mittelpunkt hinaus.

Beginnen wir nun, die Funktion für ein einzelnes Polygon aufzubauen. Dazu benötigen wir einige Variablen, die wir am besten in eine Struktur, Klasse oder sonstwas packen und den Funktionen mit auf den Weg geben. Die können sich bedienen und ihrerseits Eintragungen vornehmen.

typedef struct {
	TVector vel;        // Bewegungsvektor
	TVector dir;        // normierter Bewegungsvektor
	double  len;        // Länge des Bewegungsvektors
	double  lenlen;     // quadratische Länge
	TVector pos;        // Position der Kugel (Mittelpunkt)
	TVector intersect;  // Kollisionspunkt
	double  distance;   // Distanz bis zum Kollisionspunkt
} TCollision;

Nun der erste Teil der Funktion zur Kollisionserkennung an einem einzelnen Polygon. Ich verwende hier einen gemäßigten Pseudo-Code, d.h. ich schreibe lediglich die Vektoroperationen in verkürzter Form, um den Code etwas übersichtlicher zu machen. Aus dem Kontext dürfte hervorgehen, dass z.B. mit (vector1 * vector2) nur das Skalarprodukt gemeint sein kann, während (length * vector1) die Multiplikation eines Vektor mit einem Skalar ist.

Rückgabewert:
 1  Kollision an Polygonfläche
 2  Kollision an Kante
 3  Kollision an Ecke
-1  keine Kollision

int PolygonIntersect (TCollision *coll, TVector *v, int num) {
	int type, i, ii;
	double t0, t1;
	double curr_t, new_t; // laufende und neue t-Begrenzung
	TVector coll_point;
	TVector cp, v1, v2; // temporär

	// Radius der Kugel. Wenn es um Ellipsoide geht, muss der Radius
	// grundsätzlich auf 1 gestellt werden
	double rad = 0.1; 

	TVector nml = PlaneNormal (v[0], v[1], v[2]);
	double denom = nml * coll->vel;

	// aussteigen, wenn es auf die Rückseite der Ebene zugeht
	if (denom > 0) return -1;
	
	double plane = -(nml * v[0]);
	double dist = (nml * coll->pos) + plane;
	TBool parallel = (fabs(denom) < 0.000001);

	if (parallel) {
		// Kugel ist ständig im Schnittbereich
		t0 = 0.0;
		t1 = 1.0;

		// aussteigen, wenn Abstand zu groß
		if (fabs (dist) >= rad) return -1;	
	} else {
		// Schnittbereich berechnen
		t0 = (rad - dist) / denom;
		t1 = (-rad - dist) / denom;

		// aussteigen, wenn außerhalb des Schnittbereichs
		if (t0 > 1.0 || t1 < 0.0) return -1;
		
		// Begrenzung (siehe Abbildung oben)
		if (t0 < 0.0) t0 = 0.0;
		if (t1 > 1.0) t1 = 1.0;
	}
	...

Kollision mit der Polygonfläche

Zuerst sollten wir eines festhalten: Die Kollision an der Polygonfläche hat Priorität gegenüber der Kanten- und Eckenkollision, denn sie findet bereits an der Stelle t0 statt. Wenn wir also eine Ebenenkollision feststellen, brauchen wir die Kanten und Ecken nicht mehr zu untersuchen und können aussteigen.

Im Grunde ist die Prozedur recht einfach. Wir schieben die Kugel nach t0 und berechnen von hier aus den Intersektionspunkt, also den Berührungspunkt von Kugeloberfläche und Polygonebene, was mit Hilfe der Ebenennormalen kein Problem ist.

Die Normale der Ebene und der Kollisionspunkt auf der Kugeloberfläche

In einem zweiten Schritt prüfen wir, ob der Intersektionspunkt innerhalb des Polygons liegt. Es gibt eine Reihe von verschiedenen Verfahren, mit denen wir das feststellen können. Ich habe mich für das Verfahren der "Links-rechts-Orientierung" entschieden (siehe Werkzeugkiste), weil es sich völlig problemlos bei Polygonen mit beliebig vielen Ecken anwenden lässt. Außerdem erlaubt es die Vorausberechnung der meisten Parameter, was zu einer beachtlichen Geschwindigkeitssteigerung führen kann. Näheres dazu im 3. Teil des Tutorials.

Der Algorithmus wird u.a. von David Scherfgen vorgeschlagen und ist auf seiner Webseite http://www.scherfgen-software.net/index.php?action=tutorials&topic=collision_2 ausführlich beschrieben.

Damit haben wir schon alles zusammen und können die Funktion weiter ausbauen:

	...
	// Kollision an der Ebene ist nur sinnvoll, wenn die
	// Kugel sich nicht parallel zur Ebene bewegt
	if (parallel == False) {
		// Berechnung des Punktes, wo die Kugel
		// die Ebene berührt
		v1 = coll->pos - (rad * nml);
		v2 = t0 * coll->vel;
		TVector plane_intersect = v1 + v2;

		// Test, ob innerhalb des Polygons
		if (InsidePolygon (v, num, nml, plane_intersect)) {
			coll->distance = t0 * coll->len;
 			coll->intersect = plane_intersect;

			// Kollisionstyp 1, fertig und raus
			return 1;
		}
	}
	...

Kollision mit den Ecken und Kanten

Beginnen wir mit den Eckpunkten. Im Grunde ist das ein idealer Anwendungsfall für die umgekehrte Kollisionsberechnung (reverse intersections), bei der ein Strahl von einem Punkt aus rückwärts gegen die Kugel "geschossen" wird. Dazu können wir eine der üblichen Intersektionsroutinen (ray-sphere intersection) verwenden. Im linken Teil des Bildes ist das Verfahren angedeutet.

Reverse Intersektion (links) und das hier angewandte "Vorwärtsverfahren" (rechts)

Wir gehen hier ein wenig anders vor, indem wir die Bedingungen untersuchen, die an der Kollisionsstelle vorliegen müssen, damit es eine Berührung gibt. Dann prüfen wir, ob diese Bedingungen an irgendeiner Stelle der Bahn erfüllt sind. Oder an zwei Stellen, denn letzten Endes führt die Berechnung zu einer quadratischen Gleichung, die bis zu zwei Lösungen haben kann. Die genannten Kollisionsbedingungen sind schnell formuliert und leicht einzusehen:

1. Der Mittelpunkt der Kugel liegt auf dem Bewegungsvektor, und zwar im Intervall [t0, t1].
2. Der Mittelpunkt der Kugel hat zur Ecke des Polygons den absoluten Abstand r (Radius). Oder gleich besser, um die Absolutstriche loszuwerden: Der quadratische Abstand vom Kollisionspunkt zum Mittelpunkt ist gleich dem Quadrat des Radius. Die exakten Bedingungen:

Das Ziel ist es, die beiden Gleichungen durch Einsetzen zusammenzuführen und so umzuformen, dass wir die Normalform der quadratischen Gleichung erhalten. In diesem Fall ist die Variable natürlich t und nicht x.

Allgemeine Normalform der quadratischen Gleichung

Eine solche Gleichung lässt sich bequem lösen, wobei wir immer zuerst prüfen, was unter der Wurzel steht. Ist der Ausdruck negativ, gibt es keine reelle Lösung. Praktisch bedeutet es, dass keine Kollision stattfindet. Ist der Ausdruck = 0, gibt es nur eine Lösung, woraus wir schließen, dass die Kugel den Eckpunkt des Polygons nur streift, ein Fall ohne praktische Bedeutung. Bei positivem Ausdruck unter der Wurzel erhalten wir zwei Lösungen. Dann nehmen wir das kleinere Ergebnis, weil das größere den Intersektionspunkt auf der Rückseite der Kugel angibt - für Kollisionen uninteressant. Wenn ich mit dem Kopf gegen eine Wand renne, bekomme ich vorne eine Beule und nicht am Hinterkopf.

Am Schluss erhalten wir folgende Koeffizienten:

Interessant ist, dass a wegen des Quadrates von V nur positiv sein kann. Wenn wir die kleinere der beiden Lösungen (nächster Kollisionspunkt) suchen, brauchen wir die Wurzel nur zu subtrahieren. Im Falle der Kantenkollision es es anders, da kann der Ausdruck im Nenner negativ sein.

Nun zur Kollision mit der Kante. Wir berechnen sie auf ähnliche Weise, nur dass hier zwei Schritte erforderlich sind. Im ersten Schritt stellen wir fest, in welchem Punkt die Kugel die (unendliche) Gerade berührt, wenn überhaupt, und im zweiten Schritt prüfen wir, ob die Berührung auf dem Streckenabschnitt der Kante stattfindet.

Nun haben wir aber keinen festen Punkt mehr, auf den wir uns beziehen können. Stattdessen setzen wir den kürzesten Abstand zur Linie (die Höhe) ein und fordern, das dieser Abstand so groß sein muss wie der Radius, beides wiederum auf quadratischer Ebene.

Mit den beiden Vektoren E=S-R und B=R-A erhalten wir folgende Koeffizienten in der Normalform:

Nun brauchen wir nur noch festzustellen, ob der Punkt auf dem geforderten Streckenabschnitt, der Kante, liegt. Wie das gemacht wird, ist aus der Funktion EdgeIntersect (Werkzeugkiste) herauszulesen. Hier geht es nun mit der Funktion PolygonIntersect wie folgt weiter:

	
	...
	// Flag, ob Kollision schon festgestellt wurde
	TBool hit = False;

	// curr_t hält die nächstliegende Kollision fest und wird
	// zu Beginn auf die hintere Grenze des Schnittbereichs gesetzt
	curr_t = 1.0;

	// Kollision mit allen Ecken prüfen
	for (i=0; i<num; i++) {
		new_t = VertexIntersect (coll->pos, coll->vel, coll->lenlen,
			v[i], rad, curr_t);
		if (new_t >= 0) {
			hit = True;
			curr_t = new_t;
			coll_point = v[i];
			type = 3;
		}
	}		
		
	// Kollision mit allen Kanten prüfen
	for (i=0; i<num; i++) {
		if (i == num-1) ii = 0; else ii = i + 1; 			
		new_t = EdgeIntersect (coll->pos, coll->vel, coll->lenlen,
			v[i], v[ii], rad, curr_t, &cp);		
		if (new_t >= 0) {
			hit = True;
			curr_t = new_t;				
			coll_point = cp;
			type = 2;
		}		
	}	
	
	// Finally: Wir geben den Kollisionspunkt und die
	// Entfernung bis zum Kollisionspunkt zurück
	if (hit) {
		coll->intersect = coll_point;
		coll->distance  = curr_t * coll->len;
		return type;
	}		
	return -1;
}

Die nächstliegende Kollision

Nun, nachdem wir wissen, ob die Kugel mit einem einzelnen Polygon kollidiert und wo das geschieht, müssen wir natürlich noch alle in Frage kommenden Polygone testen und schließlich das herauspicken, welches die nächstliegende Kollisionsstelle bietet. Welche Polygone auf Grund ihrer Position zur Kugel überhaupt in Frage kommen, soll hier nicht untersucht werden, das wäre z.B. die Sache eines Tests mit bounding volumes. Darauf werde ich im dritten Teil des Tutorials ein wenig eingehen. Wenn es nur wenig Polygone gibt (nicht mehr als einige hundert), können wir für die ersten Versuche auch alle prüfen.

Ich setzte hier voraus, dass die in Frage kommenden Polygone in einem Array gesammelt sind. Dieses Array wird nun iterativ abgearbeitet. Die Vertices der Polygone werden in ein lokales Array vertices [ ] umgespeichert. Das ist zwar nur nötig, wenn wir das Verfahren auf Ellipsoide erweitern, aber so ist schon mal die Stelle gekennzeichnet, wo das erfolgen kann.

// zunächst eine mögliche Datenstruktur:
typedef struct {
	TVector Vertices[4]; // hier maximal Quads 
	int numVertices;
} TPolygon;

TPolygons Polygons[];  // Größe des Arrays dynamisch
int numPolygons;


int CollisionDetection (TCollision *coll) 
{
	TVector vertices[4];
	int colltype;
	
	// zum Festhalten der nächstliegenden Kollision
	TBool   hit;
	int     hit_type;
	double  hit_dist;
	TVector hit_point;
				
	hit = False;	
	hit_dist = 1e+10;
	hit_type = -1;

	// alle Polygone prüfen
	for (i=0; i<numPolygons; i++) {

		// Umspeichern der Vertices in ein lokales Array
		// bei Verwendung von Ellipsoiden mit Transformation
		for (v=0; v<Polygons[i].numVertices) {
			vertices[v] = Polygons[i].Vertices[v];		
		}
		colltype = PolygonIntersect 
			(coll, vertices, Polygons[i].numVertices);
		if (colltype > 0 && coll->distance < hit_dist) {
			hit       = True;
			hit_type  = colltype;
			hit_dist  = coll->distance;
			hit_point = coll->intersect;
		}
	}
	if (hit_type > 0) CollisionResponse (coll, hit_type);
	return hit_type;	
}

Kollisionsverarbeitung: Gleitebene und Gleitpfad

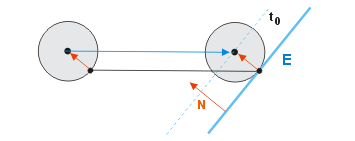
Im Falle einer positiven Kollisionserkennung reagieren wir, indem wir die Kugel auf den Gleitpfad schicken. Zunächst geht es darum, die Gleitebene zu bestimmen, und anschließend berechnen wir den genauen Pfad auf dieser Ebene. Fassen wir zusammen, welche Informationen uns die Kollisionserkennung geliefert hat: Wir haben den Kollisions- oder Intersektionspunkt, das ist der Punkt, wo die Oberfläche der Kugel die Ebene, Kante oder Ecke berührt. Ferner haben wir die Distanz der Kugel bis zum Kollisionspunkt.

Als erstes können wir schon mal die Kugel bis zur Kollisionsstelle bewegen. Es könnte sinnvoll sein, einen kleinen Abstand zu halten, damit die Kugel nicht infolge von Rundungsfehlern in die Ebene einschneidet.

Anschließend müssen wir die Gleitebene definieren, wozu wir einen Punkt sowie die Normale benötigen. Den Punkt haben wir bereits, es ist nichts anderes als der Intersektionspunkt, der immer auf der Gleitebene liegt. Und die Normale? Ganz gleich, ob Fläche, Kante oder Ecke, der Vektor vom Intersektionspunkt zum Mittelpunkt der Kugel steht senkrecht auf der Gleitebene. Er muss nur noch normalisiert werden, und schon haben wir das Gewünschte.

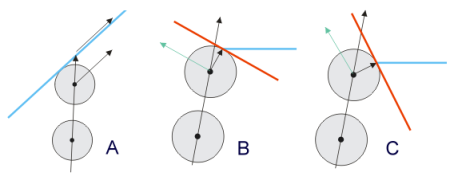
Das Bild zeigt, dass die Richtung der Gleitebene davon abhängt, wie eine Kante oder Ecke angeschnitten wird. Bei hartem Anschnitt (Fall B) wird die Kugel stärker abgelenkt als bei leichtem Anschnitt (C). Genau so möchten wir es haben.

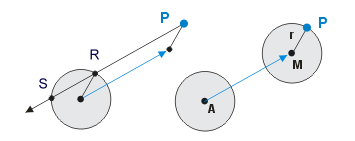
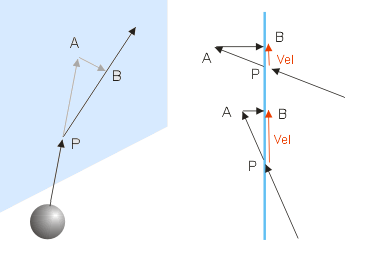
Nun ermitteln wir den genauen Pfad auf der Gleitebene. Dazu greifen wir kurz hinter die Ebene und setzen am Intersektionspunkt P noch einmal den normierten Bewegungsvektor an. So erhalten wir den Punkt A hinter der Ebene. A projizieren wir auf die Rückseite der Ebene und gewinnen den Punkt B. Der Vektor von P nach B ist nun der neue Bewegungsvektor. Wir können ihn normieren und/oder mit der alten Geschwindigkeit skalieren, je nachdem, was wir vorhaben.

So ermitteln wir den Vektor, der den Pfad auf der Gleitebene festlegt

Im rechten Teil des Bildes ist noch ein anderer Aspekt zu sehen. Der Punkt B liegt umso näher am Intersektionspunkt, je steiler der Aufprall ist. Wenn wir wollen, können wir den Abstand von P nach B in die neue Geschwindigkeit einfließen lassen, denn es liegt auf der Hand, dass bei einem steilen Aufprall (oben im Bild) mehr Bewegungsenergie verloren geht als bei einem flachen.

Wir können noch einen Schritt weiter gehen. Wenn wir die Kugel im Falle einer Kollision an das Hindernis heranschieben, haben wir ja nur einen Teil des vorgesehenen Bewegungsschrittes durchgeführt. Es könnte evtl. sinnvoll sein, im selben Frame die Bewegung zu vervollständigen, natürlich nach einer erneuten Kollisionserkennung! Die Berechnung des Gleitpfades kann uns einen Hinweis über den erforderlichen Restschritt geben. Dann müssen wir jedoch die Gleitebene auf den Mittelpunkt der Kugel beziehen und den vollen Bewegungsvektor zum Mittelpunkt addieren. Damit wir sicher hinter die Ebene greifen, können wir zusätzlich einen konstanten Vektor addieren. Der garantiert außerdem, dass eine Mindestgeschwindigkeit übrig bleibt.

Ich habe diese Aspekte allerdings nicht berücksichtigt, da ich nur den geometrischen Teil umsetzen wollte. Meiner Meinung nach ist es nicht immer günstig, physikalische Sachverhalte in den geometrischen Algorithmus einfließen zu lassen, das sollte vielmehr Aufgabe einer Physik-Engine sein. Dann allerdings muss die Physik die notwendigen Informationen über die Kollision erhalten, damit sie Kraft und Bewegung richtig berechnen kann. Zu diesen Information gehört die Steilheit des Aufpralls, die wir durch das Skalarprodukt aus dem Bewegungsvektor und der Normalen der Gleitebene bestimmen können. Wir gebrauchen das Produkt außerdem in der Kollisionsbehandlung, und zwar um zu erkennen, ob die Kugel senkrecht aufprallt. Dann lässt sich nämlich kein Gleitpfad berechnen, denn (B-P) ist ein Nullvektor.

void CollisionResponse (TCollision *coll, int type) {
	// Kugel wird zum Kollisionspunkt bewegt. Vergößern wir den 
	// Abstand (hier 0.000001), dann kann u.U. die Bewegung 
	// flüssiger werden, aber es entsteht eine Reflexionswirkung
	coll->pos = coll->pos + (coll->distance-0.000001) * coll->dir;
		
	// Gleitebene berechnen
	TVector slide_normal = coll->pos - coll->intersect;
	NormalizeVector (&slide_normal);

	// Maß für die Steilheit des Aufpralls		
	double coll_cos = slide_normal * coll->dir; 	
		
	if (fabs(coll_cos) >= 0.9999) {
		// steiler Aufprall, hier Umkehrung der Richtung
		coll->dir = -1 * coll->vel;		
	} else {
		// A = Projektionspunkt hinter der Ebene
		TVector A = coll->intersect + coll->dir;		
		double dist = PlaneIntersect 
			(coll->intersect, slide_normal, A, slide_normal);
		TVector v = dist * slide_normal;

		// B = auf die Ebene projizierter Punkt
		TVector B = A + v;
		coll->dir = B - coll->intersect;
	}
	
	// Kollisionsdaten aktualisieren
	coll->len = NormalizeVector (&coll->dir);
	coll->vel = ScaleVector (coll->len, coll->dir);
}

Der gesamte Vorgang

Zum Schluss sollten wir das Ganze noch zu einer Funktion zusammenfassen, die dann von zentraler Stelle aufgerufen wird.

void CheckCollision (double timestep) {
	// Es wird eine globale Kontrollvariable contrl vorausgesetzt,
	// in der Position und Velocity der Kugel frameübergreifend
	// gespeichert sind

	// Mit der Zeitspanne skalieren und Vektorlänge festhalten, um
	// abschließend die ursprüngliche Geschwindigkeit 
	// rekonstruieren zu können, falls gewünscht
	TVector temp_vel = ScaleVector (timestep, contrl.vel);
	double speed = VectorLength (temp_vel);
	
				
	// ------------------------------------------------------------
	// Hier ist eine geeignete Stelle für den Bounding-Test.
	// Alle in Frage kommenden Polygone, auch die des natürlichen
	// Surfaces, werden in dem Array Polygons [] gesammelt
	// (natürlich geht auch eine Index-Liste)
	// Wenn die Szenerie nicht mehr als einige hundert Polygone
	// enthält, können wir alle nehmen
	// -------------------------------------------------------------

	// -------------------------------------------------------------
	// Wenn ein Ellipsoid verwendet werden soll, ist hier die 
	// richtige Stelle, um die Matrix sowie die inverse Matrix
	// herzustellen. 
	// -------------------------------------------------------------
	
	// Nun wird die Kollisions-Struktur gefüllt. Wenn Ellipsoide 
	// verwendet werden, erfolgt die Übernahme von pos und vel
	// über eine Transformations-Matrix 
	
	TCollision coll;

	coll.pos    = contrl.pos;    // Ellipsoid: über Matrix
 	coll.vel    = temp_vel;      // Ellipsoid: über Matrix
	coll.dir    = coll.vel;
 	coll.len    = NormalizeVector (&coll.dir);
	coll.lenlen = coll.len * coll.len;

	// der Kollisionstest
	int coll_type = CollisionDetection (&coll);
	if (coll_type > 0) {
		// überflüssig, aber evtl. nützlich in der Testphase
		// Kollisionstyp anzeigen:
		PrintInteger (coll_type);

		// Flag kann auf False gesetzt werden, um bei der ersten
		// Kollision die Bewegung anzuhalten. Praktisch, um mit der
		// Kamera die Kollisionsstelle untersuchen zu können
		contrl.coll_flag = True;
	} else {
		// nix passiert, normal weiter:
		coll.pos = coll.pos + coll.vel;
	}
	
	// Kollisionsdaten für nächsten Frame festhalten
	temp_vel = coll.dir;    // Ellipsoid: über Matrix
	NormalizeVector (&temp_vel);
	contrl.vel = ScaleVector (speed/timestep, temp_vel);
	contrl.pos = coll.pos;  // Ellipsoid: über Matrix;
}

Links - Literatur

Wer nach Informationen über die beschriebene Art der Kollisionerkennung und -behandlung sucht, wird wahrscheinlich irgendwann auf folgende Internetbeiträge stoßen:

Paul Nettle: General Collision Detection for Games Using Ellipsoids http://www.gamedev.net/reference/articles/article1026.asp

Jorrit Rouwe: Collision Detection with Swept Spheres and Ellipsoids http://www.three14.demon.nl/

Kasper Fauerby: Improved Collision Detection and Response http://www.peroxide.dk/papers/collision/collision.pdf

Ich selber konnte den Artikeln eine Menge Anregungen und Informationen entnehmen und möchte mich bei den Autoren bedanken. Wer sich näher mit der Materie befassen will, sollte die Beiträge unbedingt lesen. Trotzdem halte ich es für sinnvoll, die Artikel etwas kritisch unter die Lupe zu nehmen. Paul Nettle beschreibt sehr knapp, jedoch vollständig ein relativ einfaches Verfahren, das aber leider einige Mängel aufweist. Die Kantenkollision funktioniert nicht sauber, besonders bei schrägem Anschnitt (etwa < 43°) wird die Kollision nur noch unzuverlässig erkannt. Der Grund: Nettle verwendet dafür ein grobes Näherungsverfahren, das hier an seine Grenzen stößt. Auch der mitgelieferte Pseudocode ist etwas oberflächlich und ungenau und kann nicht direkt umgesetzt werden.

Jorrit Rouwe geht ganz anders vor. Sein Verfahren ist recht aufwendig, scheint aber genau zu sein und macht in der Praxis einen robusten Eindruck. Der Artikel ist mathematisch ziemlich anspruchsvoll verfasst und dürfte Anfängern nur mit Vorbehalt zu empfehlen sein. Die Umsetzung ist teilweise sehr eigenwillig, und wer einen gradlinigen, effizienten Code bevorzugt, wird mit Jorrits Code kaum etwas anfangen können. Hinzu kommt, dass der Code in einem schwer übertragbaren Stil, der alle Register von C++ zieht, verfasst ist. Gleichwohl enthält der Beitrag eine Reihe von wichtigen und nützlichen Informationen, vor allem, wenn es um die mathematischen Sachverhalte geht.

Kasper Fauerby übernimmt weitgehend das Verfahren von Rouwe, beschreibt es aber ausführlich und in flüssiger, leicht nachvollziehbarer Weise. Angenehm zu lesen, auch für Einsteiger! Den Code von Rouwe hat Fauerby drastisch vereinfacht und damit besser lesbar gemacht. Aber er wirkt etwas unaufgeräumt und ist nach meinem Empfinden in der Gesamtkonzeption nicht sehr schlüssig.

Und was ist mit dem Algorithmus in diesem Tutorial? Zuerst hatte ich mich an Nettle orientiert. Durch eine Reihe von Änderungen konnte ich die genannten Schwächen zwar nahezu ausmerzen, aber eben nur nahezu. Daraufhin habe ich mich bei Rouwe / Kauerby umgesehen und fand deren Verfahren deutlich präziser. So sind schließlich deren Grundgedanken in den Algorithmus eingeflossen, während ich den Code, abgesehen von einigen Passagen, neu geschrieben habe.

Damit bin ich beim Ausblick auf den 3. Teil des Tutorials angelangt, wo ich im Zusammenhang mit dem Ellipsoid erneut auf die erwähnten Artikel zu sprechen kommen werde. Ansonsten wird es dort vor allem um Erweiterungen des Verfahrens gehen, wobei der Kernalgorithmus, den ich hier vorgestellt habe, weitgehend erhalten bleibt. Geplant sind hauptsächlich folgende Punkte:

• Aufbereitung der Daten zum Zeichnen der Szenerie und zur Kollisionserkennung,
• Verwendung von Ellipsoiden anstatt einer Kugel,
• einfache Vorselektion mit Hilfe von bounding volumes,
• Mehrfacherkennungen und "Kollisionsbremsen"

Noch ein letzter Hinweis: Für diejenigen, die mit Pascal vertraut sind und sich mit C überhaupt nicht auskennen, habe ich eine kleine Übersetzungshilfe auf meine Homepage gestellt: http://www.erinacom.de/ogl/collision/translate.html

Und jetzt wünsche ich viel Erfolg mit der Kugel. Möge sie stets den richtigen Weg finden und nicht zu eigenwillig sein.

Reinhard