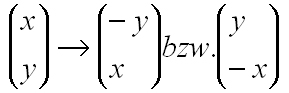Version vom 3. April 2007, 18:11 Uhr

Kollisionserkennung

zweier Polygone mit dem Separating Axis Theorem

Vorwort

In diesem Tutorial möchte ich eine schnelle Variante zur Kollision zweier konvexer Polygone erläutern. Diese kann nachträglich für konkave Polygone und andere Objekte wie Kreise und abgerundete Objekte verwendet werden. Um den mathematischen Hintergrund zu verstehen, ist es sinnvoll ein wenig Kenntnis in [wiki]Vektorrechnung[/wiki] zu haben.

Die Theorie

Das Separating Axis Theorem (im folgenden mit SAT abgekürzt) besagt, dass zwei Polygone sich nicht schneiden, wenn es möglich ist, eine Gerade zu finden, die zwischen den beiden liegt. Nun gibt es unendlich viele Geraden die man testen könnte... Glücklicherweise kann man sich hier auf eine überschaubare Zahl beschränken, denn man braucht nur die Anzahl der Seiten beider Polygone. Bei einem Viereck wären das vier, bei einem Dreieck drei, etc. Hat man die Eckpunkte des Polygons als Vektoren (Ortsvektoren) gegeben, kann man durch Subtraktion zweier Ortsvektoren den Vektor bestimmen der zu der Seite gehört, die von den beiden Vektoren aufgespannt wird.

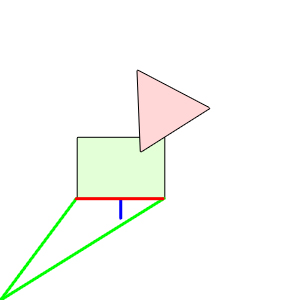
Auf dem Bild rechts ist ein Beispiel zu sehen. Dort ist ein Quadrat, die grünen Striche bezeichnen die Ortsvektoren der Eckpunkte, der rote Strich ist die berechnete Seite. Was wir aber brauchen ist der blaue Strich, das ist die Normale der Seite. Die Normale berechnet sich folgendermaßen:

die Koordinaten werden vertauscht und eine von beiden wird negiert. Der Vektor muss dann noch normalisiert werden, sodass er die Länge 1 erhält. Jetzt müssen beide Polygone auf diesen Vektor projeziert werden, denn dadurch haben wir ein Eindimensionales Abbild unserer Polygone und können mittels eines einfachen Vergleichs überprüfen, ob sich die beiden 1D-Strecken schneiden. Sollte ein Fall eintreffen bei dem kein Schnitt stattfindet, dann kollidieren die beiden Polygone nicht und die Prozedur kann abgebrochen werden. Nun zur Projektion:

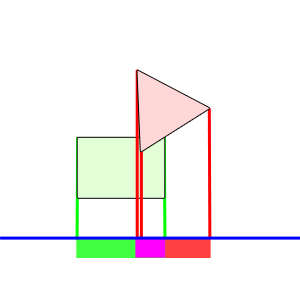
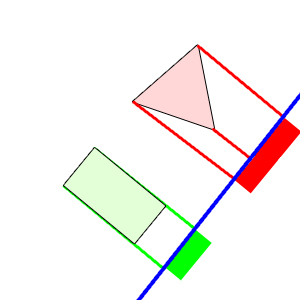
Auf dem linken Bild sieht man, wie beide Polygone auf die Gerade projeziert werden, der pinke Bereich zeigt die Schnittmenge an. In diesem Fall ist die Gerade die Normale der linken oder rechten Seite des Quadrats. Auf dem Bild rechts ist der Fall dargestellt, dass keine Kollision stattfindet, demzufolge gibt es auch keine Schnittmenge auf der Geraden. Dazu ist allerdings zu sagen, dass die Gerade keine räumliche Position hat. So wie Vektoren auch keine Positionen haben, Vektoren sind lediglich verschiebungsanweisungen und unsere "Gerade" wie ich sie hier nenne, ist auch nur ein Vektor, denn wo sie liegt ist letzten endes egal, da wir ja ein eindimensionales Ergebnis anstreben.

Für die Projektion eines Vektors auf einen anderen verwenden wir das Skalarprodukt, bei diesem kommt ein Zahlenwert heraus, der die Position des Eckpunktes auf unserer 1D-Geraden darstellt. Haben wir sämtliche Punkte projeziert, so müssen wir für die jeweiligen Polygone noch jeweils den kleinsten und größten Wert heraussuchen, damit wir zwei Strecken erhalten. Diese werden dann auf Schnitt geprüft und das wars.

Zusammenfassung

• Jedes der beiden Polygone durchgehen und alle nötigen Geraden aus den Normalen der Seitenflächen bestimmen
  • Jeden Eckpunkt jedes Polygons auf diese Geraden Projezieren
  • Die kleinsten und größten Werte ermitteln und auf Schnitt prüfen
• Tritt der Fall auf, dass kein Schnitt statt findet, so kann sofort abgebrochen werden, es findet keine Kollision statt.

Der Code

Um bei so vielen Vektoroperationen nicht völlig durcheinander zu geraten und die Übersicht zu verlieren (was dabei durchaus mal passieren kann), ist es es sinnvoll, sich eine Unit zu schreiben, die einem die Vektorrechnung abnimmt. Im weiteren Verlauf des Tutorials werde ich folgende Unit benutzen:

// Unit Vectors
(**************************************************

- Enthält: TVector2f

**************************************************)

unit Vectors;

interface

type
  // 2D Vektor
  TVector2f = record
    X, Y: Extended;
  end;

  // Zwei Singles in einen TVector2f umwandeln
  function To_v2f(X, Y: Single): TVector2f;
  // Zwei Vektoren addieren
  function v2f_Add(V1, V2: TVector2f): TVector2f;
  // Einen Vektor von einem anderen subtrahieren
  function v2f_Sub(V1, V2: TVector2f): TVector2f;
  // Einen Vektor skalieren
  function v2f_Scale(V: TVector2f; Scalar: Single): TVector2f;
  // Ermittelt die Länge eines Vektors
  function v2f_Length(V: TVector2f): Single;
  // Normalisiert einen Vektor (sodass v2f_length = 1)
  function v2f_Normalize(V: TVector2f): TVector2f;
  // Ermittelt ds Skalarprodukt
  function v2f_DotProduct(V1, V2: TVector2f): Single;

implementation

function To_v2f(X, Y: Single): TVector2f;
begin
  Result.X := X;
  Result.Y := Y;
end;

function v2f_Add(V1, V2: TVector2f): TVector2f;
begin
  Result.X := V1.X + V2.X;
  Result.Y := V1.Y + V2.Y;
end;

function v2f_Sub(V1, V2: TVector2f): TVector2f;
begin
  Result.X := V1.X - V2.X;
  Result.Y := V1.Y - V2.Y;
end;

function v2f_Scale(V: TVector2f; Scalar: Single): TVector2f;
begin
  Result.X := V.X * Scalar;
  Result.Y := V.Y * Scalar;
end;

function v2f_Length(V: TVector2f): Single;
begin
  Result := sqrt(V.X * V.X + V.Y * V.Y);
end;

function v2f_Normalize(V: TVector2f): TVector2f;
var
  L: Single;
begin
  L := v2f_Length(V);

  if L = 0 then
    L := 1;

  Result := v2f_Scale(V, 1 / L);
end;

function v2f_DotProduct(V1, V2: TVector2f): Single;
begin
  Result := V1.X * V2.X + V1.Y * V2.Y;
end;

end.

Jedoch schadet es nicht, sich eine eigene zu schreiben, um seine Kenntnisse in Sachen Vektorrechnung ein wenig zu festigen. Jetzt benötigen wir eine Klasse für unsere Polygone. Die einzelnen Eckpunkte der Polygone werden nicht etwa absolut (also in Weltkoordinaten), sondern relativ zu einem Punkt angegeben, so fällt es leichter, das Polygon zu verschieben. Der absolute Wert kann jedoch ganz nützlich sein, um z.B. ein Polygon zu zeichnen. Als erstes definieren wir ein Array von TVector2f, denn jeder Eckpunkt ist ein Vektor und unsere Polygone sollen ja beliebig viele davon besitzen können, also:

type
  TV2fArray = array of TVector2f;

Dann folgt die Definition unseres Polygons:

  TPolygon = class
  private
    fposition: TVector2f;                             // Position
    fvertices: TV2fArray;                             // Vertices (Objektkoordinaten)
    function GetVertex(n: integer): TVector2f;        // Liefert die Objektkoordinaten
    function GetVertexAbs(n: integer): TVector2f;     // Liefert die absoluten Koordinaten
    function GetCount: integer;                       // Liefert length(fvertices)
  public
    procedure AddVertex(v: TVector2f);
    procedure RemoveVertex(n: integer);
    property position: TVector2f read fposition write fposition;                // Position
    property vertices[n: integer]: TVector2f read GetVertex;                    // Vertex Koordinaten
    property vertices_abs[n: integer]: TVector2f read GetVertexAbs;
    property Count: integer read GetCount;                                      // siehe GetCount
  end;

Unser Polygon hat jetzt eine Position und Eckpunkte, ebenfalls können wir auf absolute, sowie relative Koordinaten zugreifen. Count liefert uns die Anzahl der Ecken. [size=9][i](Eine Ecke bezeichnet man auch als Vertex, der Plural von Vertex ist Vertices.)[/i][/size] Hier sind die entsprechenden Funktionen:

procedure TPolygon.AddVertex(v: TVector2f);
begin
  setlength(fvertices, length(fvertices) + 1);
  fvertices[high(fvertices)] := v;
end;

procedure TPolygon.RemoveVertex(n: integer);
var
  i: integer;
begin
  for i := n to high(fvertices) - 1 do
    fvertices[i] := fvertices[i + 1];
  setlength(fvertices, length(fvertices) - 1);  
end;

function TPolygon.GetVertex(n: integer): TVector2f;
begin
  result := fvertices[n];
end;

function TPolygon.GetVertexAbs(n: integer): TVector2f;
begin
  result := v2f_add(fvertices[n], fposition);
end;

function TPolygon.GetCount: integer;
begin
  result := length(fvertices);
end;

Mit AddVertex können wir unsere Vertices hinzufügen, aber dazu später mehr. Nun folgt die Kollisionserkennung an sich:

function PolyPolyIntersect(A, B: TPolygon): boolean;
var
  i, j, l: integer;
  tmp, proj, voffset: TVector2f;
  dp, amin, amax, bmin, bmax, d1, d2, foffset: extended;
begin
  // Offset berechnen
  voffset := v2f_sub(A.position, B.position);
// A - alle Projektionsgeraden ermitteln und projezieren
  for i := 0 to (a.count - 1) do
  begin
    l := i + 1;
    if l > (a.count - 1) then
      l := 0;
    // Berechnung der Seitenfläche
    tmp := v2f_sub(a.vertices[l], a.vertices[i]);
    // Berechnet die Normale der Seitenfläche
    proj := v2f_normalize(to_v2f(-tmp.y, tmp.x));
    // Projeziert den ersten Wert
    amin := v2f_dotproduct(a.vertices[0], proj);
    amax := amin;
    // Findet den kleinsten und größten projezierten Wert für die Gerade für A
    for j := 1 to (a.count - 1) do
    begin
      // projezieren
      dp := v2f_dotproduct(a.vertices[j], proj);
      if dp < amin then
        amin := dp;
      if dp > amax then
        amax := dp;
    end;
    // s.o.
    bmin := v2f_dotproduct(b.vertices[0], proj);
    bmax := bmin;
    // B
    for j := 1 to (b.count - 1) do
    begin
      dp := v2f_dotproduct(b.vertices[j], proj);
      if dp < bmin then
        bmin := dp;
      if dp > bmax then
        bmax := dp;
    end;
    // 1D Kollision
    foffset := v2f_dotproduct(voffset, proj);
    amin := amin + foffset;
    amax := amax + foffset;
    d1 := amin - bmax;
    d2 := bmin - amax;
    // Wenn es keine Überschneidung gibt, abbrechen -> keine Kollision
    if (d1 > 0) or (d2 > 0) then
    begin
      result := false;
      exit;
    end;
  end;
// B - alle Projektionsgeraden ermitteln und projezieren (s.o.)
  for i := 0 to (b.count - 1) do
  begin
    l := i + 1;
    if l > (b.count - 1) then
      l := 0;
    tmp := v2f_sub(b.vertices[l], b.vertices[i]);
    proj := v2f_normalize(to_v2f(-tmp.y, tmp.x));
    amin := v2f_dotproduct(a.vertices[0], proj);
    amax := amin;
    for j := 1 to (a.count - 1) do
    begin
      dp := v2f_dotproduct(a.vertices[j], proj);
      if dp < amin then
        amin := dp;
      if dp > amax then
        amax := dp;
    end;
    bmin := v2f_dotproduct(b.vertices[0], proj);
    bmax := bmin;
    for j := 1 to (b.count - 1) do
    begin
      dp := v2f_dotproduct(b.vertices[j], proj);
      if dp < bmin then
        bmin := dp;
      if dp > bmax then
        bmax := dp;
    end;
    foffset := v2f_dotproduct(voffset, proj);
    amin := amin + foffset;
    amax := amax + foffset;
    d1 := amin - bmax;
    d2 := bmin - amax;
    if (d1 > 0) or (d2 > 0) then
    begin
      result := false;
      exit;
    end;
  end;
  // Kollision
  result := true;
end;

Wie man sieht, ist der zweite Teil des Codes, mit dem ersten sogut wie identisch, der einzige Unterschied besteht darin, dass dort die Geraden aus den Vertices von B berechnet werden. Nehmen wir den Code mal auseinander:

    tmp := v2f_sub(a.vertices[l], a.vertices[i]);
    proj := v2f_normalize(to_v2f(-tmp.y, tmp.x));

Hier wird zunächst der Vektor berechnet, der für die Seitenfläche steht, durch die Schleife wird dies für alle Seitenflächen gemacht. Danach wird die Normale berechnet. proj ist dann der Vektor auf den wir unsere Vertices projezieren.

    amin := v2f_dotproduct(a.vertices[0], proj);
    amax := amin;

Hier projezieren wir das erste Vertex von A und haben somit den ersten Punkt unserer Strecke.

    for j := 1 to (a.count - 1) do
    begin
      dp := v2f_dotproduct(a.vertices[j], proj);
      if dp < amin then
        amin := dp;
      if dp > amax then
        amax := dp;
    end;

Hier werden alle weiteren Vertices projeziert und der kleinste, sowie größte Wert gespeichert. Das gleiche wird für B wiederholt.

    foffset := v2f_dotproduct(voffset, proj);
    amin := amin + foffset;
    amax := amax + foffset;
    d1 := amin - bmax;
    d2 := bmin - amax;

Da es sich bei unseren Vertexkoordinaten um Objektkoordinaten handelt, müssen die projezierten Vertices nun um die Differenz beider Polygonpositionen verschoben werden. Dies klingt zunächst einmal kompliziert, macht aber sinn. Die Alternative wäre, jeden Punkt in Weltkoordinaten (also absolute Koordinaten) umzuwandeln. Dadurch, dass wir am Anfang den Vektor zwischen den beiden Polygonen berechnen:

voffset := v2f_sub(A.position, B.position);

und ihn danach Projezieren, können wir diese Verschiebung auf unserer Geraden nachträglich vornehmen und haben somit alles in einem Abwasch erledigt.

    if (d1 > 0) or (d2 > 0) then
    begin
      result := false;
      exit;
    end;

Ohne einen Vergleich kommt auch diese Kollisionsabfrage nicht aus, hier jedoch nur auf eindimensionaler Ebene. Gibt es keine Überschneidung der beiden 1D-Strecken, so kann die Prozedur abgebrochen werden, denn es gibt keine Kollision. Ist die komplette Prozedur durchgelaufen ohne abzubrechen, so wird result auf true gesetzt und eine Kollision ist bestätigt.

Das Beispielprojekt

Was wäre ein Tutorial doch ohne Beispiel ;) Ich werde hier nur kurz die Verwendung des Codes erläutern und ein kleines Beispielprogramm anhängen. Ein Polygon muss natürlich erst einmal erzeugt werden:

A := TPolygon.Create;

Die einfachste Möglichkeit es zu gestalten funktioniert so:

  with A do
  begin
    position := to_v2f(200, 200);
    AddVertex(to_v2f(50, -50));
    AddVertex(to_v2f(50, 50));
    AddVertex(to_v2f(-50, 50));
    AddVertex(to_v2f(-50, -50));
  end;

Dies liefert ein Quadrat mit den Maßen 100*100 an der Position (200|200).

Zeichnen kann man das Polygon ganz einfach so:

procedure TMainForm.DrawPolygon(A: TPolygon);
var
  i, l: integer;
begin
  for i := 0 to A.Count - 1 do
  begin
    l := i + 1;
    if l > (A.Count - 1) then
      l := 0;
    Image1.Canvas.MoveTo(round(A.vertices_abs[l].x), round(A.vertices_abs[l].y));
    Image1.Canvas.LineTo(round(A.vertices_abs[i].x), round(A.vertices_abs[i].y));
  end;
end;

Und hier das Beispielprojekt:

Exe: http://www.exec-dev.de/SAT_Tutorial/SAT_exe.zip

Source: http://www.exec-dev.de/SAT_Tutorial/SAT_src.zip

Links

Separating Axis Theorem

SAT-Tutorial(Eng): http://www.harveycartel.org/metanet/tutorials/tutorialA.html

SAT-Tutorial(Eng / VB) http://gpwiki.org/index.php/VB:Tutorials:Building_A_Physics_Engine:Basic_Intersection_Detection

Nachwort

Ich hoffe das Tutorial war nicht zu trocken und hat vielleicht auch ein wenig Spass gemacht und weitergeholfen. Für Fragen, Vorschläge, Ergänzungen, etc. bin ich selbstverständlich offen.

mfg