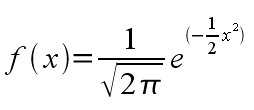Blur: Unterschied zwischen den Versionen
(→Begriffsklärung) |
(→Theorie) |
||
| Zeile 35: | Zeile 35: | ||
[[Bild:Anaconda blurred.jpg]] | [[Bild:Anaconda blurred.jpg]] | ||
| + | |||
| + | |||
| + | Das Schwierige am Blurren ist es nun, alle Pixel durch Faktoren so zu gewichten, dass die Summer der Faktoren 1 ergibt. Ist das nicht der Fall, kann es passieren, dass man die Helligkeit, Sättigung oder andere Farbelemente verfälscht. Dazu folgendes Gedankenexperiment: Man will ein Bild so blurren, dass nur das mittlere Pixel und alle direkt anliegenden (insgesamt acht) Pixel in die Berechnung miteinbezogen werden. Dem mittleren Pixel gibt man nun einen bestimmten Faktor, als Beispiel hier 0,5. Die Faktoren für die anderen Pixel müssen also in der Addition auch 0,5 ergeben. Man kann hier auf die schnelle mit 0,5 / 8 = 0,0625 als Faktor arbeiten, aber dabei bleibt unbeachtet, dass die Pixel an den Ecken (bzw deren Zentren) weiter vom mittleren Pixel entfernt sind, als die anderen äußeren Pixel. Bei diesem Beispiel kann man das noch vernachlässigen bzw per Hand anpassen. Da aber der Blur-Effekt bei so einer kleinen Matrix nicht sehr stark zur Geltung kommt, werden oft viel mehr umliegende Pixel mit in die Rechnung einbezogen. Wenn man dann das Ganze noch per Hand machen will, hat man ein Problem. | ||
| + | |||
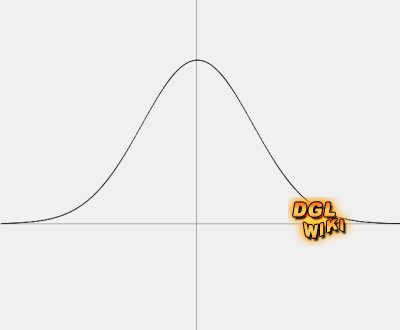
| + | Als Lösung verwendet man die Gaußsche Glockenkurve. Diese Kurve bzw ihre Formel stellt einen Graph dar, dessen Flächeninhalt zur x-Achse von minus bis plus unendlich genau 1 ergibt, sie sieht etwa so aus: | ||
| + | |||
| + | |||
| + | [[Bild:Glocke.jpg]] | ||
| + | |||
| + | |||
| + | Die Funktion sieht so aus: | ||
| + | |||
| + | |||
| + | [[Bild:Dichtefkt.jpg]] | ||
| + | |||
| + | |||
| + | ... | ||
Version vom 27. Oktober 2006, 16:31 Uhr
Bitte haben Sie etwas Geduld und nehmen Sie keine Änderungen vor, bis der Artikel hochgeladen wurde. |
Blur
Begriffsklärung
In dem man einen Blur-Effekt, zu deutsch Weichzeichnen-Effekt, auf eine Textur oder allgemein ein Bild anwendet, gibt man ihm eine Unschärfe. Im richtigen Leben begegnet man diesem Effekt zum Beispiel bei falsch eingestellten Beamer- oder Overheadprojektoren. Auch beim Fotografieren kann es sein, dass bei falscher Linseneinstellung das Bild sehr unscharf wird - wobei man in diesem Fall genaugenommen von Defokussierung und nicht von Unschärfe spricht.
Blur wird seit langem in Computerspielen, -bildern und -animationen verwendet, um zum Beispiel die Aufmerksamkeit von unwichtigen Objekten auf Wichtige lenken oder (bei Actionspielen) um anzuzeigen, dass der Spieler getroffen wurde. Vor allem in Rennspielen trifft man heutzutage oft auf den Motion-Blur-Effekt. Hier wird das Bild nicht gleichmäßig weichgezeichnet, sondern in eine bestimmte Richtung verwischt, wodurch der Eindruck eine schnellen Bewegung entsteht beziehungsweise verstärkt wird.
Theorie
Das Prinzip des Blurrens ist sehr einfach zu verstehen. Man stelle sich ein scharfes Bild vor:
Zoomen wir nun ganz nahe an das Bild heran:
Jetzt folgt der Trick: Man gibt jedem Pixel die durchschnittliche Farbe der Pixel, die um das aktuelle herum liegen. Je nach Anwendung wird meist das aktuelle Pixel am höchsten gewichtet, je weiter sich die anderen Pixel davon befinden, desto weniger werden diese gewichtet. Damit erhält man folgenden Bildausschnitt (Zoom):
Zoomt man wieder heraus, dann kommt der Effekt richtig zur Geltung:
Das Schwierige am Blurren ist es nun, alle Pixel durch Faktoren so zu gewichten, dass die Summer der Faktoren 1 ergibt. Ist das nicht der Fall, kann es passieren, dass man die Helligkeit, Sättigung oder andere Farbelemente verfälscht. Dazu folgendes Gedankenexperiment: Man will ein Bild so blurren, dass nur das mittlere Pixel und alle direkt anliegenden (insgesamt acht) Pixel in die Berechnung miteinbezogen werden. Dem mittleren Pixel gibt man nun einen bestimmten Faktor, als Beispiel hier 0,5. Die Faktoren für die anderen Pixel müssen also in der Addition auch 0,5 ergeben. Man kann hier auf die schnelle mit 0,5 / 8 = 0,0625 als Faktor arbeiten, aber dabei bleibt unbeachtet, dass die Pixel an den Ecken (bzw deren Zentren) weiter vom mittleren Pixel entfernt sind, als die anderen äußeren Pixel. Bei diesem Beispiel kann man das noch vernachlässigen bzw per Hand anpassen. Da aber der Blur-Effekt bei so einer kleinen Matrix nicht sehr stark zur Geltung kommt, werden oft viel mehr umliegende Pixel mit in die Rechnung einbezogen. Wenn man dann das Ganze noch per Hand machen will, hat man ein Problem.
Als Lösung verwendet man die Gaußsche Glockenkurve. Diese Kurve bzw ihre Formel stellt einen Graph dar, dessen Flächeninhalt zur x-Achse von minus bis plus unendlich genau 1 ergibt, sie sieht etwa so aus:
Die Funktion sieht so aus:
...