Vektorprodukt: Unterschied zwischen den Versionen
Aus DGL Wiki
K (→Rechenregeln: Mathe. Symbole) |
K (Rechtschreibfehler) |
||
| Zeile 1: | Zeile 1: | ||
== Vektorprodukt == | == Vektorprodukt == | ||
=== Übersicht === | === Übersicht === | ||
| − | Das Vektorprodukt (Vektrorkreuzprodukt, Kreuzprodukt) wird eingesetzt, um einen Vektor zu finden, der | + | Das Vektorprodukt (Vektrorkreuzprodukt, Kreuzprodukt) wird eingesetzt, um einen Vektor zu finden, der senkrecht zu 2 bekannten Vektoren steht. Diese Vektoren können z.B. 2 Richtungen entlang eines Dreiecks sein, woraus man dann die Flächen-[[Normalen|Normale]] des Dreiecks berechnen kann, was zur Berechnung von [[Beleuchtungs|Licht]]-Effekten wichtig ist. Zusätzlich kann man damit Flächeninhalte berechnen. |
=== Definition === | === Definition === | ||
| Zeile 8: | Zeile 8: | ||
# aχb steht senkrecht zu a und zu b, also a•(aχb) = b•(aχb) = 0, wo "•" für das [[Standard Skalarprodukt]] steht. | # aχb steht senkrecht zu a und zu b, also a•(aχb) = b•(aχb) = 0, wo "•" für das [[Standard Skalarprodukt]] steht. | ||
# a,b, aχb bilden ein Rechtssystem, d.h. stellt man die Vektoren mit den Fingern in der richtigen Reihenfolge dar, so benötigt man die rechte Hand (Daumen, Zeigefinger, Mittelfinger) und nicht die linke Hand. | # a,b, aχb bilden ein Rechtssystem, d.h. stellt man die Vektoren mit den Fingern in der richtigen Reihenfolge dar, so benötigt man die rechte Hand (Daumen, Zeigefinger, Mittelfinger) und nicht die linke Hand. | ||
| − | # ||aχb||=||a||*||b||*sin(φ) (0 ≤ φ ≤ π) ( Wird zur Berechnung der Parallelogrammfläche genutzt. Durch | + | # ||aχb||=||a||*||b||*sin(φ) (0 ≤ φ ≤ π) ( Wird zur Berechnung der Parallelogrammfläche genutzt. Durch Halbierung erhält man die Dreiecksfläche. ) |
Für a=(a<sub>1</sub>;a<sub>2</sub>;a<sub>3</sub>), b=(b<sub>1</sub>;b<sub>2</sub>;b<sub>3</sub>) berechnet sich das Vektorprodukt durch: | Für a=(a<sub>1</sub>;a<sub>2</sub>;a<sub>3</sub>), b=(b<sub>1</sub>;b<sub>2</sub>;b<sub>3</sub>) berechnet sich das Vektorprodukt durch: | ||
Version vom 12. Oktober 2006, 17:33 Uhr
Inhaltsverzeichnis
Vektorprodukt
Übersicht
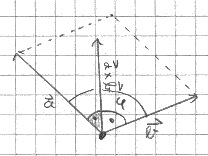
Das Vektorprodukt (Vektrorkreuzprodukt, Kreuzprodukt) wird eingesetzt, um einen Vektor zu finden, der senkrecht zu 2 bekannten Vektoren steht. Diese Vektoren können z.B. 2 Richtungen entlang eines Dreiecks sein, woraus man dann die Flächen-Normale des Dreiecks berechnen kann, was zur Berechnung von Licht-Effekten wichtig ist. Zusätzlich kann man damit Flächeninhalte berechnen.
Definition
Das eindeutige Vektorprodukt aχb zweier Vektoren (a,b) ist definiert durch:
- aχb steht senkrecht zu a und zu b, also a•(aχb) = b•(aχb) = 0, wo "•" für das Standard Skalarprodukt steht.
- a,b, aχb bilden ein Rechtssystem, d.h. stellt man die Vektoren mit den Fingern in der richtigen Reihenfolge dar, so benötigt man die rechte Hand (Daumen, Zeigefinger, Mittelfinger) und nicht die linke Hand.
- ||aχb||=||a||*||b||*sin(φ) (0 ≤ φ ≤ π) ( Wird zur Berechnung der Parallelogrammfläche genutzt. Durch Halbierung erhält man die Dreiecksfläche. )
Für a=(a1;a2;a3), b=(b1;b2;b3) berechnet sich das Vektorprodukt durch:
a2*b3 - a3*b2
aχb = a3*b1 - a1*b3
a1*b2 - a2*b1
Die drei Zeilen stehen hier natürlich für die drei Komponenten des Vektors aχb.
Rechenregeln
Es gilt:
- bχa = - (aχb)
- Linearität:
λ*(aχb) = (λ*a)χb = aχ(λ*b) (λ reel) (a+c)χb = aχb + cχb aχ(b+c) = -(b+c)χa = -(bχa + cχa) = aχb + aχc