shader ConeVolumeShadow: Unterschied zwischen den Versionen
K (→Geometrie-Crashkurs) |
K (→Funktionsweise) |
||
| (11 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
| − | |||
=Shadername= | =Shadername= | ||
Zurück zur [[Shadersammlung]] | Zurück zur [[Shadersammlung]] | ||
| Zeile 21: | Zeile 19: | ||
== Voraussetzungen == | == Voraussetzungen == | ||
Aufgrund der besonderen Funktionsweise funktioniert dieser Shader nur dann, wenn es sich bei sämtlichen Objekte in der Szene die einen Schatten werfen sollen um Kugeln handelt. Des weiteren muss innerhalb der Anwendung manuell berechnet werden welches Objekt auf welches andere Objekt einen Schatten wirft. Je mehr Objekte ein Schatten auf ein einzelnes Objekt werfen, desto langsamer wird das Verfahren. | Aufgrund der besonderen Funktionsweise funktioniert dieser Shader nur dann, wenn es sich bei sämtlichen Objekte in der Szene die einen Schatten werfen sollen um Kugeln handelt. Des weiteren muss innerhalb der Anwendung manuell berechnet werden welches Objekt auf welches andere Objekt einen Schatten wirft. Je mehr Objekte ein Schatten auf ein einzelnes Objekt werfen, desto langsamer wird das Verfahren. | ||
| + | |||
| + | Möglicherweise lässt sich das beschriebene Verfahren auch auf andere einfache geometrische Objekte verallgemeinern. In Frage kommen etwa Planetenringe. Auf diese Möglichkeiten geht dieser Artikel jedoch nicht weiter ein. | ||
| + | |||
| + | Der hier vorgestellte Shader geht von nur einer einzigen Lichtquelle aus. Der Ansatz lässt sich aber problemlos auf mehrere Lichtquellen erweitern. Allerdings steigt damit natürlich der Rechenaufwand. | ||
== Geometrie-Crashkurs == | == Geometrie-Crashkurs == | ||
| Zeile 47: | Zeile 49: | ||
== Funktionsweise == | == Funktionsweise == | ||
| − | Verwendet man eine | + | Kommen wir nun zum eigentlichen Shader. Verwendet man eine Punktlichtquelle hat das Schatten-Volumen einer Kugel eine sehr einfache Form, nämliche die eines Kreiskegels. Da eine Punktlichtquelle aber unschöne harte Schatten wirft, wollen wir hier eine Kugellichtquelle verwenden. Eine Kugellichtquelle besteht aus unendlich vielen Punktlichtquellen die kugelförmig um ein Zentrum angeordnet sind. Da bei dieser Lichtquelle das Licht aus leicht unterschiedlichen Richtungen auf das Objekt fällt entstehen, wie in der Realität, weiche Schatten. |
| + | |||
| + | Das Schatten-Volumen einer von einer Kugellichtquelle beleuchteten Kugel lässt sich durch zwei Kreiskegel beschreiben. Dies machen wir uns zu nutze. Wie auf dem folgenden Bild erkennbar gibt es einen inneren Kegel (''inner cone'') und einen äußeren Kegel (''outer cone''). Befinden wir uns außerhalb des äußeren Kegels erhalten wir die volle Lichtstärke, da der Occluder keine Auswirkungen hat. Innerhalb des inneren Kegels befinden wir uns dagegen vollständig im Schatten. Die dritte Möglichkeit ist eine Position innerhalb des äußeren aber außerhalb des inneren Kegels. Hier ist die Halbschattenzone die für den weichen Schatten sorgt. | ||
[[Bild:shader_ConeVolumeSoftShadow.png]] | [[Bild:shader_ConeVolumeSoftShadow.png]] | ||
| + | |||
| + | Die Hauptachse beider Kegel liegt, wie zu erkennen ist, auf der Geraden durch Lichtquelle <tt>L</tt> und Occluder <tt>O</tt>. Im Shader beschreiben wir beide Kegel durch den Radius an zwei Punkten, nämlich den Radius auf Höhe der Lichtquelle und auf Höhe des Occluders. Für den äußeren Kegel bedienen wir uns eines Tricks, den wir nehmen für die Lichtquelle einfach einen negativen Radius an. Die Beschreibung beider Kegel ist also bis auf das Vorzeichen des Lichtquellenradius bei beiden Kegeln identisch. Wir haben damit genug Daten um den Radius an jeder Stelle beider Kegel zu berechnen. | ||
| + | |||
| + | Der Punkt <tt>F</tt> ist die Position des gerade gerenderten Fragments. Der erste Schritt besteht nun darin den Punkt <tt>F'</tt> zu berechnen. Eine detaillierte Erklärung dazu findet sich im [[#Geometrie-Crashkurs|vorhergehenden Abschnitt]]. Den Abstand zwischen <tt>F</tt> und <tt>F'</tt> bezeichnen wir als <tt>rF</tt>. | ||
| + | |||
| + | Nun geht es darum den Radius des inneren und äußeren Kegels (<tt>rF_inner</tt> bzw. <tt>rF_outer</tt>) auf Höhe von F' zu berechnen. Dies geht über den beliebten Dreisatz, die nötigen Formeln finden sich oben im Bild. Der einzige Unterschied bei beiden Formeln liegt nur im Vorzeichen für den Radius der Lichtquelle. | ||
| + | |||
| + | Es folgt eine große Fallunterscheidung die ermittelt in welcher Zone (Licht/Halbschatten/Vollschatten) wir uns befinden. Das Ergebnis ist ein Faktor <tt>s</tt> der später mit der Beleuchtung multipliziert wird. Dabei steht <tt>1.0</tt> für volles Licht und <tt>0.0</tt> für Dunkelheit. Zu beachten ist, dass <tt>rF_inner</tt> auch negativ werden kann. In dem Fall befinden wir uns soweit hinter dem Occluder, dass keine Vollschatten-Zone mehr existiert. | ||
| + | <source lang="c">if (dLF' < dLO || rF >= rF_outer) { | ||
| + | // Fragment vor dem Occluder oder außerhalb des äußeren Kegels. | ||
| + | s = 1.0; | ||
| + | } | ||
| + | else if (rF_inner >= rF) { | ||
| + | // Wir befinden uns im Vollschatten | ||
| + | s = 0.0; | ||
| + | } | ||
| + | else if (rF_inner >= 0 || rF >= -rF_inner) { | ||
| + | // Wir befinden uns im Halbschatten, lineare Interpolation | ||
| + | s = (rF - rF_inner) / (rF_outer - rF_inner); | ||
| + | } | ||
| + | else { | ||
| + | // Wir empfangen Licht von zwei Richtungen, also oben und unten am Occluder vorbei. | ||
| + | // Die beiden rF heben sich gegenseitig auf. | ||
| + | s = (-2*rF_inner) / (rF_outer - rF_inner); | ||
| + | }</source> | ||
| + | |||
| + | {{Hinweis|Eine kleine Randnotiz: Der Schatten wird orthogonal zur Geraden <tt>LO</tt> interpoliert. Diese Berechnung ist nicht physikalisch korrekt. Allerdings dürfte der Unterschied niemandem auffallen.}} | ||
==Code== | ==Code== | ||
| + | ====Das "Drumherum"==== | ||
| + | Im wesentlichen gibt es zwei Dinge zu beachten: | ||
| + | # Wann immer man geometrische Berechnungen durchführt muss man darauf achten das alle Punkte und Vektoren im gleichen Koordinatenraum vorliegen. Der hier vorgestellte Shader arbeitet im View-Space und erwartet daher auch die Daten der Lichtquelle und der Occluder-Objekte im View-Space.<br>Liegen also z.B. die Koordinaten der Lichtquelle in Weltkoordinaten vor, müssen sie vor Übergabe an den Shader mit der View-Matrix (das was z.B. [[gluLookAt]] produziert) multipliziert werden. | ||
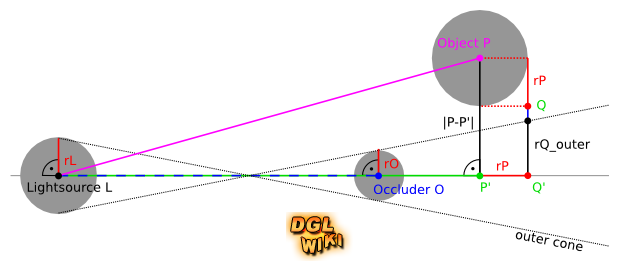
| + | # Die Anzahl der Occluder die an den Shader übergeben werden sollte so klein wie möglich sein. Aus diesem Grund sollte man Objekte ausschließen die sowieso keine Auswirkungen auf das gerade gerenderte Objekt haben. Wir müssen also Objekte ausschließen die vollständig außerhalb des äußeren Kegels liegen. Ein derartiger Test funktioniert zumindest für Kugeln ähnlich wie der den wir im Shader für einzelne Punkte machen. Hier addieren/subtraieren wir aber noch an geeigneter Stelle den Radius des getesteten Objektes. Letztlich vergleichen wir die Länge von <tt>|P-P'| - rP</tt> mit der Länge von <tt>rQ_outer</tt>. Dieser Ansatz ist zwar nicht exakt, meldet aber niemals ein Objekt außerhalb, wenn es eigentlich innerhalb liegt. Umgekehrt kann dies allerdings passieren, da eigentlich der Punkt <tt>Q</tt> geprüft wird. | ||
| + | |||
| + | : [[Bild:shader_ConeVolumeExclude.png]] | ||
| + | |||
====Vertexshader==== | ====Vertexshader==== | ||
Der Vertexshader ist nichts besonderes. Er transformiert einfach nur die Vertexposition sowie die Normale und gibt die Daten weiter. Dieser Shader ist im wesentlichen aus UltimateConquest übernommen. Daher werden hier Vertexattribute und Matrixuniforms selbst definiert. Sofern man noch mit OpenGL 2.x arbeitet kann man aber problemlos die dort verfügbaren eingebauten Uniforms und Attribute benutzen. | Der Vertexshader ist nichts besonderes. Er transformiert einfach nur die Vertexposition sowie die Normale und gibt die Daten weiter. Dieser Shader ist im wesentlichen aus UltimateConquest übernommen. Daher werden hier Vertexattribute und Matrixuniforms selbst definiert. Sofern man noch mit OpenGL 2.x arbeitet kann man aber problemlos die dort verfügbaren eingebauten Uniforms und Attribute benutzen. | ||
Aktuelle Version vom 18. Mai 2018, 20:48 Uhr
Inhaltsverzeichnis
Shadername
Zurück zur Shadersammlung
| Beschreibung | Autor | Version |
|---|---|---|
| Kegelvolumen-Schatten | Coolcat | 1.0 |
Bilder
Voraussetzungen
Aufgrund der besonderen Funktionsweise funktioniert dieser Shader nur dann, wenn es sich bei sämtlichen Objekte in der Szene die einen Schatten werfen sollen um Kugeln handelt. Des weiteren muss innerhalb der Anwendung manuell berechnet werden welches Objekt auf welches andere Objekt einen Schatten wirft. Je mehr Objekte ein Schatten auf ein einzelnes Objekt werfen, desto langsamer wird das Verfahren.
Möglicherweise lässt sich das beschriebene Verfahren auch auf andere einfache geometrische Objekte verallgemeinern. In Frage kommen etwa Planetenringe. Auf diese Möglichkeiten geht dieser Artikel jedoch nicht weiter ein.
Der hier vorgestellte Shader geht von nur einer einzigen Lichtquelle aus. Der Ansatz lässt sich aber problemlos auf mehrere Lichtquellen erweitern. Allerdings steigt damit natürlich der Rechenaufwand.
Geometrie-Crashkurs
Um den Shader zu verstehen ist ein wenig Geometrie-Wissen erforderlich, insbesondere bezüglich des Skalarproduktes. Wer meint das Skalarprodukt und seine Eigenschaften schon zu kennen, kann diesen Abschnitt einfach überspringen. Wenn etwas unklar ist kann man ja noch einmal hierher zurückkommen.
Das Skalarprodukt, häufig auch als Dot-Product bezeichnet, ist für zwei 3D-Vektoren a und b wie folgt definiert:
- dot(a,b) := a.x*b.x + a.y*b.y + a.z*b.z
Der Betrag |a| eines Vektors a ist als dessen Länge bezüglich der euklidischen Norm definiert. Dies ist im wesentlichen der gute alte Pythagoras für drei Dimensionen:
- |a| := sqrt(a.x*a.x + a.y*a.y + a.z*a.z)
Eine wichtige Eigenschaft dieses Skalarproduktes ist, dass sich darüber der Winkel w zwischen den beiden Vektoren bestimmen lässt. Es gilt:
- dot(a,b) = |a| * |b| * cos(w)
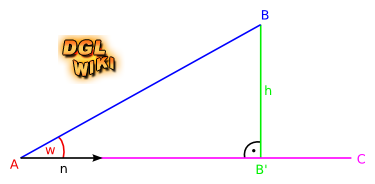
Dies wollen wir ausnutzen. In der folgenden Zeichnung sind und die Punkte A, B und C bekannt. Wir wollen B' und die Strecke h berechnen, also B im rechten Winkel auf den Vektor AC projizieren.
Mit Hilfe des Skalarproduktes ist dies recht einfach. Zunächst berechnen wir den Vektor AB := B - A, sowie den Vektor AC := C - A. Letzteren normalisieren wir, indem wir durch die Länge teilen: n := AC / |AC|. Da n die Länge 1 hat gilt:
- dot(AB, n) = |AB| * cos(w)
Aus der Mittelstufe sollte bekannt sein, dass der Kosinus wie folgt definiert ist:
- cos(w) = Ankathete / Hypotenuse
Die Hypotenuse ist hier die Strecke |AB| und die Ankathete ist die gesuchte Strecke |AB'| := |B' - A|. Es gilt also:
- cos(w) = Ankathete / Hypotenuse
- <=> cos(w) = |AB'| / |AB|
- <=> |AB| * cos(w) = |AB'|
- <=> dot(AB, n) = |AB'|
Da n normalisiert war lässt sich der Punkt B' nun leicht berechnen: B' := A + n * |AB'|. Die Strecke h berechnet sich aus dem Abstand zwischen B und B', also h := |B - B'|.
Funktionsweise
Kommen wir nun zum eigentlichen Shader. Verwendet man eine Punktlichtquelle hat das Schatten-Volumen einer Kugel eine sehr einfache Form, nämliche die eines Kreiskegels. Da eine Punktlichtquelle aber unschöne harte Schatten wirft, wollen wir hier eine Kugellichtquelle verwenden. Eine Kugellichtquelle besteht aus unendlich vielen Punktlichtquellen die kugelförmig um ein Zentrum angeordnet sind. Da bei dieser Lichtquelle das Licht aus leicht unterschiedlichen Richtungen auf das Objekt fällt entstehen, wie in der Realität, weiche Schatten.
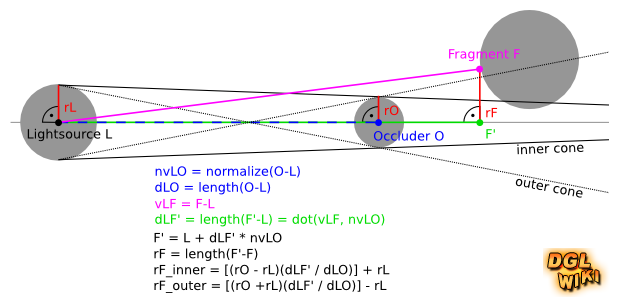
Das Schatten-Volumen einer von einer Kugellichtquelle beleuchteten Kugel lässt sich durch zwei Kreiskegel beschreiben. Dies machen wir uns zu nutze. Wie auf dem folgenden Bild erkennbar gibt es einen inneren Kegel (inner cone) und einen äußeren Kegel (outer cone). Befinden wir uns außerhalb des äußeren Kegels erhalten wir die volle Lichtstärke, da der Occluder keine Auswirkungen hat. Innerhalb des inneren Kegels befinden wir uns dagegen vollständig im Schatten. Die dritte Möglichkeit ist eine Position innerhalb des äußeren aber außerhalb des inneren Kegels. Hier ist die Halbschattenzone die für den weichen Schatten sorgt.
Die Hauptachse beider Kegel liegt, wie zu erkennen ist, auf der Geraden durch Lichtquelle L und Occluder O. Im Shader beschreiben wir beide Kegel durch den Radius an zwei Punkten, nämlich den Radius auf Höhe der Lichtquelle und auf Höhe des Occluders. Für den äußeren Kegel bedienen wir uns eines Tricks, den wir nehmen für die Lichtquelle einfach einen negativen Radius an. Die Beschreibung beider Kegel ist also bis auf das Vorzeichen des Lichtquellenradius bei beiden Kegeln identisch. Wir haben damit genug Daten um den Radius an jeder Stelle beider Kegel zu berechnen.
Der Punkt F ist die Position des gerade gerenderten Fragments. Der erste Schritt besteht nun darin den Punkt F' zu berechnen. Eine detaillierte Erklärung dazu findet sich im vorhergehenden Abschnitt. Den Abstand zwischen F und F' bezeichnen wir als rF.
Nun geht es darum den Radius des inneren und äußeren Kegels (rF_inner bzw. rF_outer) auf Höhe von F' zu berechnen. Dies geht über den beliebten Dreisatz, die nötigen Formeln finden sich oben im Bild. Der einzige Unterschied bei beiden Formeln liegt nur im Vorzeichen für den Radius der Lichtquelle.
Es folgt eine große Fallunterscheidung die ermittelt in welcher Zone (Licht/Halbschatten/Vollschatten) wir uns befinden. Das Ergebnis ist ein Faktor s der später mit der Beleuchtung multipliziert wird. Dabei steht 1.0 für volles Licht und 0.0 für Dunkelheit. Zu beachten ist, dass rF_inner auch negativ werden kann. In dem Fall befinden wir uns soweit hinter dem Occluder, dass keine Vollschatten-Zone mehr existiert.
if (dLF' < dLO || rF >= rF_outer) {
// Fragment vor dem Occluder oder außerhalb des äußeren Kegels.
s = 1.0;
}
else if (rF_inner >= rF) {
// Wir befinden uns im Vollschatten
s = 0.0;
}
else if (rF_inner >= 0 || rF >= -rF_inner) {
// Wir befinden uns im Halbschatten, lineare Interpolation
s = (rF - rF_inner) / (rF_outer - rF_inner);
}
else {
// Wir empfangen Licht von zwei Richtungen, also oben und unten am Occluder vorbei.
// Die beiden rF heben sich gegenseitig auf.
s = (-2*rF_inner) / (rF_outer - rF_inner);
}
| |
Eine kleine Randnotiz: Der Schatten wird orthogonal zur Geraden LO interpoliert. Diese Berechnung ist nicht physikalisch korrekt. Allerdings dürfte der Unterschied niemandem auffallen. |
Code
Das "Drumherum"
Im wesentlichen gibt es zwei Dinge zu beachten:
- Wann immer man geometrische Berechnungen durchführt muss man darauf achten das alle Punkte und Vektoren im gleichen Koordinatenraum vorliegen. Der hier vorgestellte Shader arbeitet im View-Space und erwartet daher auch die Daten der Lichtquelle und der Occluder-Objekte im View-Space.
Liegen also z.B. die Koordinaten der Lichtquelle in Weltkoordinaten vor, müssen sie vor Übergabe an den Shader mit der View-Matrix (das was z.B. gluLookAt produziert) multipliziert werden. - Die Anzahl der Occluder die an den Shader übergeben werden sollte so klein wie möglich sein. Aus diesem Grund sollte man Objekte ausschließen die sowieso keine Auswirkungen auf das gerade gerenderte Objekt haben. Wir müssen also Objekte ausschließen die vollständig außerhalb des äußeren Kegels liegen. Ein derartiger Test funktioniert zumindest für Kugeln ähnlich wie der den wir im Shader für einzelne Punkte machen. Hier addieren/subtraieren wir aber noch an geeigneter Stelle den Radius des getesteten Objektes. Letztlich vergleichen wir die Länge von |P-P'| - rP mit der Länge von rQ_outer. Dieser Ansatz ist zwar nicht exakt, meldet aber niemals ein Objekt außerhalb, wenn es eigentlich innerhalb liegt. Umgekehrt kann dies allerdings passieren, da eigentlich der Punkt Q geprüft wird.
Vertexshader
Der Vertexshader ist nichts besonderes. Er transformiert einfach nur die Vertexposition sowie die Normale und gibt die Daten weiter. Dieser Shader ist im wesentlichen aus UltimateConquest übernommen. Daher werden hier Vertexattribute und Matrixuniforms selbst definiert. Sofern man noch mit OpenGL 2.x arbeitet kann man aber problemlos die dort verfügbaren eingebauten Uniforms und Attribute benutzen.
uniform mat4 uModelViewProjection;
uniform mat4 uModelView;
uniform mat3 uNormalMatrix;
attribute vec3 aPosition;
attribute vec3 aNormal;
attribute vec2 aTexCoord;
varying vec3 vPosition;
varying vec3 vNormal;
varying vec2 vTexCoord;
void main() {
gl_Position = uModelViewProjection * vec4(aPosition, 1.0);
vPosition = (uModelView * vec4(aPosition, 1.0)).xyz;
vNormal = normalize(uNormalMatrix * aNormal);
vTexCoord = aTexCoord;
}
Fragmentshader
Der Fragmentshader macht den eigentlich Job. Es handelt sich um einen aufgeblasenen Per-Pixel-Light-Shader. Zusätzlich zur normalen Diffuse-Beleuchtung wird in der Funktion shadowFactor() auch noch ein Schattenfaktor berechnet. Diese Funktion berechnet das Produkt sämtlicher Kegelvolumen für das aktuelle Fragment. Am Ende erhalten wir einen Wert zwischen 0.0 und 1.0 der dann einfach mit der Diffuse-Beleuchtung verrechnet wird.
uniform sampler2D uTexture;
// the lightsource described by position and radius
uniform vec4 uLightsource;
vec3 lsPosition = uLightsource.xyz;
float lsRadius = uLightsource.w;
// each shadow volume is described by position (xyz) and radius (w) of the occluder packed into a single vec4
const int shadowMaxCount = 5;
uniform vec4 uShadows[shadowMaxCount];
uniform int uShadowCount;
varying vec3 vPosition;
varying vec3 vNormal;
varying vec2 vTexCoord;
const vec3 cAmbient = vec3(0.025,0.025,0.025);
// simple local diffuse per-pixel lighting
float diffuseFactor() {
vec3 lightDir = normalize(lsPosition-vPosition);
vec3 normal = normalize(vNormal);
return max(dot(lightDir, normal), 0.0);
}
// process all shadow volumes
float shadowFactor() {
float s = 1.0;
// iterate all shadow volumes
for (int i=0; i<uShadowCount; ++i) {
// extract data
vec4 occluder = uShadows[i];
vec3 ocPosition = occluder.xyz;
float ocRadius = occluder.w;
// project fragment (vPosition) on the cone axis => F_
vec3 nvLO = ocPosition - lsPosition;
float dLO = length(nvLO);
nvLO /= dLO;
vec3 vLF = vPosition - lsPosition;
float dLF_ = dot(vLF, nvLO);
if (dLF_ < dLO) {
// fragment before occluder => no shadow
continue;
}
vec3 F_ = lsPosition + dLF_ * nvLO;
float rF = distance(F_, vPosition);
// compute outer and inner radius at F_
float rF_outer = (ocRadius + lsRadius) * (dLF_ / dLO) - lsRadius;
if (rF >= rF_outer) {
// outside the outer cone => no shadow
continue;
}
float rF_inner = (ocRadius - lsRadius) * (dLF_ / dLO) + lsRadius;
if (rF_inner >= rF) {
// inside the inner cone => full shadow
return 0.0;
}
else if (rF_inner >= 0.0 || rF >= -rF_inner) {
// soft shadow, linear interpolation
s *= (rF - rF_inner) / (rF_outer - rF_inner);
}
else {
// light from both sides of the occluder
s *= (-2.0*rF_inner) / (rF_outer - rF_inner);
}
}
return s;
}
void main() {
vec3 texcolor = texture2D(uTexture, vTexCoord).xyz;
gl_FragColor.xyz = cAmbient * texcolor;
float lightFactor = diffuseFactor();
if (lightFactor > 0.004) {
// don't compute shadows for fragments that are already dark from local lighting
lightFactor *= shadowFactor();
}
gl_FragColor.xyz += texcolor * lightFactor;
gl_FragColor.w = 1.0;
}