Tutorial Lektion 2: Unterschied zwischen den Versionen
DGLBot (Diskussion | Beiträge) K (Der Ausdruck ''<pascal>(.*?)</pascal>'' wurde ersetzt mit ''<source lang="pascal">$1</source>''.) |
(→Der erste Kontakt) |
||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 37: | Zeile 37: | ||
=== Der erste Kontakt === | === Der erste Kontakt === | ||
| − | Um nun etwas mit OpenGL rendern zu können, müssen wir uns bewusst werden, was | + | Um nun etwas mit OpenGL rendern zu können, müssen wir uns bewusst werden, was eine Modellmatrix ist und warum wir sie benötigen. In dieser Matrix wird nämlich festgehalten, '''wie''' und '''wo''' ein Objekt gezeichnet wird. Das hört sich vielleicht zunächst recht merkwürdig an, lässt sich aber leicht veranschaulichen. |
| − | + | Mann sollte sich vorstellen das eigentlich zwei Koordinatensysteme existieren, keine Angst ist ganz einfach... ;). | |
| + | Ich erkläre es Euch an einer Beispielzeichnung: | ||
| + | |||
| + | [[Bild:weltkoordinatensystem-vs-modellkoordinatensystem.png]] | ||
| + | |||
| + | Also in der 3D-Programmierung verschiebt man eigentlich nicht das Objekt sondern das Koordinatensystem, alles verstanden? *fg* Gut, dann weiter. Da man nun ein Objekt im Weltkoordinatensystem nicht so einfach verschieben und drehen kann (versucht mal die neuen Koordinaten eines beliebig gedrehten Würfels selber zu berechnen), also suchte man etwas, was an Stelle des Weltkoordinatensystems verschoben werden könnte, und so einfach zu Handhaben war wie eine '''unrotierte Darstellung im Ursprung des Koordinatensystems'''. Wer mitgelesen hat wird es schon wissen... richtig! Es ist das Modellkoordinatensystem, von selbst darauf gekommen? Super! | ||
| + | |||
| + | Das Modellkoordinatensystem liegt noch vor dem ersten Aufruf parallel zum Weltkoordinatensystem, also die Basisvektoren (x,y,z-Achsen) "zeigen" in die selbe Richtung und haben den selben Ursrpung (0-Punkt). Rufen wir nun eine OpenGL Funktion zur Veränderung (z.B. glTranlate, glRotate...) unseres Objektes auf, so ändern wir eigentlich nicht das Objekt sondern nur das Modellkoordinatensystem. Und nicht vergessen! Auch beim Programmieren definieren wir ja auch zuerst die Position (also das Modellkoordinatensystem) und dann zeichnen wird das Objekt, ist eigentlich nicht schwer zu verstehen oder? *g* | ||
| + | |||
| + | Ok, ok... ;) eine Beispielzeichnung: | ||
| + | |||
| + | [[Bild:wc-vs-mc-beispiel.png]] | ||
| + | |||
| + | Der Würfel in der Darstellung oben, ist eigentlich nicht notwendig und dient nur der Veranschaulichung. | ||
| + | |||
| + | |||
| + | Sollte es jemand also nach der folgenden Erläuterung nicht verstanden haben, kann er mich selbstverständlich persönlich per Mail zur "Rechenschaft" ziehen oder aber er wirft einen Blick in unser OpenGLWiki :)). | ||
| + | |||
| + | Wir setzen also zu Beginn unser Modellkoordinatensystem in den Mittelpunkt unseres Weltkoordinatensystems. Um oberes Beispiel aufzugreifen: Den Bildschirm. Dies geschieht mit dem Befehl [[glLoadIdentity]] und entspricht einem Reset der Modellmatrix. Theoretisch können wir nun an dieser Stelle etwas zeichnen. Dies würde allerdings dazu führen, dass das Objekt sehr groß oder gar nicht zu sehen ist, weil der Punkt (auch Augpunktkoordinate genannt) von dem aus wir unser Objekt betrachten sich genau an der Stelle befindet wo sich unser Objekt befindet, nämlich im Ursprung (vorausgesetzt wir Zeichnen ein Objekt um oder and den Ursprung, und das genau in der x/y-Ebene und nicht darüber oder darunter) . Gehen wir doch einmal 6 Einheiten nach hinten und 1,5 Einheiten nach links! | ||
| + | |||
| + | Eine kleine Beispielgrafik soll helfen: | ||
| + | |||
| + | [[Bild:objekt-sichtbar-verschieben.png]] | ||
| − | |||
Hierfür sollte man sich bewusst werden, dass wir in OpenGL praktisch an einen Stuhl gefesselt sind, d.h. wir können uns gar nicht bewegen. Das soll uns aber nicht davon abhalten. Wir brauchen ja nur die ganze Welt so zu bewegen, dass es für uns aussieht, als ob wir uns bewegen. Denn wenn sich alles außer uns nach links bewegt, haben wir den Eindruck, wir wären nach rechts gewandert, right? | Hierfür sollte man sich bewusst werden, dass wir in OpenGL praktisch an einen Stuhl gefesselt sind, d.h. wir können uns gar nicht bewegen. Das soll uns aber nicht davon abhalten. Wir brauchen ja nur die ganze Welt so zu bewegen, dass es für uns aussieht, als ob wir uns bewegen. Denn wenn sich alles außer uns nach links bewegt, haben wir den Eindruck, wir wären nach rechts gewandert, right? | ||
Nun aber zu der Bewegung unseres ersten Objektes: | Nun aber zu der Bewegung unseres ersten Objektes: | ||
| − | <source lang="pascal">glTranslatef( | + | <source lang="pascal">glTranslatef(0, 0,-6); |
| − | glTranslatef(0, 0 | + | glTranslatef(-1.5,0,0); |
| − | Dies hat bewirkt, dass sich unser Zeichenstift 1,5 Einheiten nach links (negativer Bereich der X-Achse) | + | </source> |
| + | Dies hat bewirkt, dass sich unser Zeichenstift 6 Einheiten nach hinten (negativer Bereicht der Y-Achse) und anschließend 1,5 Einheiten nach links (negativer Bereich der X-Achse) bewegt hat. Ich habe diesen Fall absichtlich in zwei Schritten gefasst, um es zu verdeutlichen. Sicherlich wäre es einfacher, alles mit nur einem Aufruf von [[glTranslate|glTranslate*]] zu machen: | ||
<source lang="pascal">glTranslatef(-1.5, 0,-6);</source> | <source lang="pascal">glTranslatef(-1.5, 0,-6);</source> | ||
Man beachte, dass in diesem Fall die 6 Schritte nach hinten notwendig sind um ein bisschen Distanz zum Objekt zu bekommen und nicht direkt in ihm zu stehen! | Man beachte, dass in diesem Fall die 6 Schritte nach hinten notwendig sind um ein bisschen Distanz zum Objekt zu bekommen und nicht direkt in ihm zu stehen! | ||
Fertig! Schon haben wir dort unseren "Zeichenstift" positioniert, der nun auf weitere Zeichenkommandos von uns wartet. Das mag sicherlich alles ein wenig verwirrend klingen... probiert es am Besten aus und spielt mit den Parametern und erkennt, was gemeint ist :). | Fertig! Schon haben wir dort unseren "Zeichenstift" positioniert, der nun auf weitere Zeichenkommandos von uns wartet. Das mag sicherlich alles ein wenig verwirrend klingen... probiert es am Besten aus und spielt mit den Parametern und erkennt, was gemeint ist :). | ||
| + | |||
== Von Sichtungen... == | == Von Sichtungen... == | ||
=== Die Büchse der Pandora === | === Die Büchse der Pandora === | ||
| Zeile 99: | Zeile 122: | ||
'''Euer'''<br> | '''Euer'''<br> | ||
'''Phobeus''' | '''Phobeus''' | ||
| + | |||
| + | == Dateien == | ||
| + | * Der aktuellste Beispiel-Quelltext befindet sich im DGLSDK 2006.1 für {{ArchivLink|file=dglsdk_win32_2006_1|text=Windows}} und {{ArchivLink|file=dglsdk_linux_2006_1|text=Linux}} | ||
| + | * {{ArchivLink|file=tut_lektion_2_delphi_api|text=Alter Delphi-API-Quelltext zum Tutorial}} | ||
| + | * {{ArchivLink|file=tut_lektion_2_delphi_vcl|text=Alter Delphi-VCL-Quelltext zum Tutorial}} | ||
| + | * {{ArchivLink|file=tut_lektion_2_exe|text=Windows-Binary zum Tutorial}} | ||
{{TUTORIAL_NAVIGATION | [[Tutorial Lektion 1]] | [[Tutorial Lektion 3]]}} | {{TUTORIAL_NAVIGATION | [[Tutorial Lektion 1]] | [[Tutorial Lektion 3]]}} | ||
[[Kategorie:Tutorial|Lektion2]] | [[Kategorie:Tutorial|Lektion2]] | ||
Aktuelle Version vom 23. Juli 2009, 01:45 Uhr
Inhaltsverzeichnis
Entdeckung einer neuen Welt
Vorwort
Ich möchte Euch an dieser Stelle bei DGL herzlich willkommen heißen. Vermutlich wird dies eines der ersten Tutorials sein, das Ihr als Einsteiger lesen werdet. Wahrscheinlich werdet Ihr dann auch noch nicht lange bei uns sein und Euch nicht vorstellen können, dass all die Schreiber auf unserer Seite keine Gurus, sondern ganz normale Menschen sind.
Man kann uns also jeder Zeit im Forum "anfassen", uns Fragen stellen, Vorschläge unterbreiten oder einfach nur einmal kurz mit einem Lob ermutigen weitere Texte zu verfassen ;-).
Ich wünsche Euch an dieser Stelle viel Erfolg bei dem Einstieg in die Thematik OpenGL und ermahne Euch noch einmal, dass Ihr Eure Ziele nicht zu weit steckt. Wirklich Spaß beginnt OpenGL nämlich erst dann zu machen, wenn man stets kleinere Erfolge feiern kann.
Höhere Mächte - Matrizen und ihre Folgen
Saubere Arbeit
Bevor wir direkt beginnen, etwas zu zeichnen, müssen wir erst einmal das Bild löschen, denn wie in der vorherigen Lektion beschrieben zeichnen wir die Szene jeden Schleifendurchlauf neu. Das Löschen der Puffer, in dem die Bildinformationen enthalten sind, übernimmt die Funktion glClear. Die Farbinformationen unser Fragmente (Fragmente sind vergleichbar mit den Pixeln auf dem Bildschirm, besitzen aber weitere Informationen wie z. B. Tiefenwerte. Bei der Ausgabe des Bildes werden diese Fragmente in Pixel umgewandelt) sind in dem so genannten Farbpuffer (Colorbuffer) gespeichert. Aus diesem Grund übergeben wir an die Funktion glClear die Konstante GL_COLOR_BUFFER_BIT. Die oben bereits angesprochenen Tiefenwerte stehen im Tiefenpuffer. Diese Daten werden benutzt, um zu entscheiden, welche Pixel durch andere verdeckt werden. Deshalb sollten wir den Tiefenpuffer auch mit löschen. Die Konstante dafür heißt GL_DEPTH_BUFFER_BIT.
//Farbbuffer und Tiefenpuffer entleeren
glClear(GL_COLOR_BUFFER_BIT or GL_DEPTH_BUFFER_BIT);
Mit Hilfe des Befehls glClearColor können wir festlegen, welche Farbinformationen mit dem Aufruf von glClear in den Colorbuffer geschrieben werden sollen. Wenn wir es also genau nehmen, so löscht glClear den Colorbuffer nicht, sondern es schreibt ihn mit den definierten Werten voll. Standardmäßig erhalten die Fragmente eine schwarze Farbe. (Der Vollständigkeit halber sei erwähnt, dass der Tiefenpuffer immer mit Nullen überschrieben wird.)
Es wird also nicht bei jedem Zeichenvorgang (Rendervorgang) der Bildspeicher gelöscht, sondern der Programmierer entscheidet, wann dies geschehen soll. Theoretisch könnt Ihr auch die Szene wiedergeben und dann löschen, bevor sie ausgegeben wird... wer's mag :).
Wer sich entscheidet, den Colorbuffer nicht zu löschen, der kann so auch einige nette Effekte erzeugen. Den Cheatern unter euch sollte der erreichte Effekt bekannt vorkommen, wenn man beispielsweise bei Counter-Strike durch die Wand gelaufen ist. Der Grund für das Verwischen ist in beiden Fällen derselbe: Das neue Bild wird gezeichnet, ohne dass das alte Bild aus dem Puffer entfernt wurde.
Und die Welt ist doch keine Scheibe...
Nachdem wir nun wieder Ordnung im Speicher geschafft haben, können wir zum interessanten Teil kommen: "Wie darf man sich einen 3D-Raum vorstellen?" Nun... warum schaut Ihr Euch nicht einmal in Eurem Zimmer um?
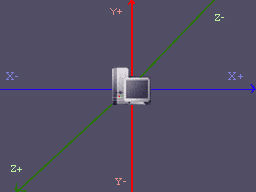
Versuchen wir doch mal, ein Beispiel direkt aus dem Leben gegriffen zu nehmen und stellen uns unsere Umgebung als Koordinaten-System vor (Igitt!). Der Monitor, der hoffentlich direkt vor uns steht, ist in diesem Fall unser Ursprung, d.h. er liegt an dem Punkt (0, 0, 0).
Blicken wir seitwärts neben den Monitor, so sehen wir eine Linie (wenn Ihr es nicht tun solltest, macht Euch keine Sorgen ... solche Anfälle hat der Autor häufiger *g*), die von links nach rechts verläuft. Es handelt sich hierbei um die X-Achse, die links vom Monitor im negativen Bereich verläuft, rechts davon in den positiven.
Nun blicken wir einmal nach oben und einmal nach unten und schon erspähen wir die Y-Achse, die oberhalb des Monitors positiv verläuft, unterhalb negativ. Wunderbar! Wenn Ihr bereits in 2D gearbeitet habt, solltet Ihr an dieser Stelle ein dümmliches Grinsen auf Eurem Gesichte haben und das wohltuende Gefühl, dass Euch das doch alles bereits irgendwie bekannt vorkommt. Doch zu unserem Entsetzen können wir uns ja auch noch von unserem Bildschirm wegbewegen oder auch dichter heran (alle Kurzsichtigen unter uns sollten das nicht so persönlich nehmen, auch sie leben in einem 3D-Raum ^__-).
Dieses Phänomen ist im 3D-Raum typisch, jedoch nicht unerklärlich, da wir uns auf der Z-Achse bewegen. Rollen wir mit dem Stuhl vom Monitor weg, so gelangen wir in den positiven Bereich der Z-Achse, bewegen wir uns drauf zu, gelangen wir in den negativen Bereich. Jeder, der bereits in D3D programmiert hat, sollte sich schleunigst einprägen, dass das ein großer Unterschied zwischen D3D und OpenGL ist. Das kann sonst zu einigen wirklich fiesen Fehlern führen, wenn man es nicht weiß... *fg*.
Soweit so gut! Klingt bisher hoffentlich immer noch nicht so kompliziert. Nur keine Sorge, das Niveau versuchen wir zu halten ;).
Speziell wenn Ihr bereits 2D-Spiele programmiert habt, solltet Ihr Euch sehr schnell von folgenden Gedanken trennen: Die Koordinaten, die Ihr seht und angebt, entsprechen in der Regel nicht den Pixeln des Bildschirmes, sondern so genannten Weltkoordinaten. Eine Definition für diese Weltkoordinaten gibt es nicht, denn wie groß diese sind, ist dem Programmierer überlassen. Ob Ihr euer Objekt eine Einheit vor Euch und 0,1 Einheit rechts von Euch oder aber 100 Einheiten vor euch und 10 Einheiten neben Euch positioniert ist egal. Die euch zur Verfügung stehende Welt ist grenzenlos ;). Ihr könnt Eure Szene theoretisch unendlich klein oder aber unendlich groß darstellen. Das Einzige, was euch wirklich daran hindert, ist die Größe und Auflösung der Euch zur Verfügung stehenden Typen wie Integer oder Single ;). Der eigentliche Größeneindruck eines Objektes entsteht durch die Geschwindigkeit mit der sich der Betrachter und andere Objekte in der Welt bewegen.
Der erste Kontakt
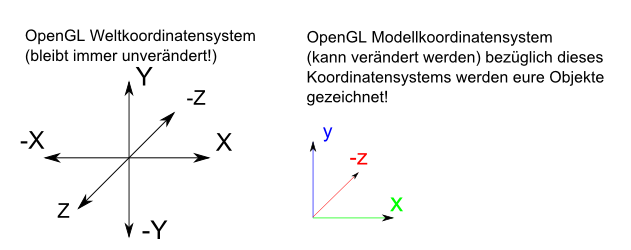
Um nun etwas mit OpenGL rendern zu können, müssen wir uns bewusst werden, was eine Modellmatrix ist und warum wir sie benötigen. In dieser Matrix wird nämlich festgehalten, wie und wo ein Objekt gezeichnet wird. Das hört sich vielleicht zunächst recht merkwürdig an, lässt sich aber leicht veranschaulichen.
Mann sollte sich vorstellen das eigentlich zwei Koordinatensysteme existieren, keine Angst ist ganz einfach... ;). Ich erkläre es Euch an einer Beispielzeichnung:
Also in der 3D-Programmierung verschiebt man eigentlich nicht das Objekt sondern das Koordinatensystem, alles verstanden? *fg* Gut, dann weiter. Da man nun ein Objekt im Weltkoordinatensystem nicht so einfach verschieben und drehen kann (versucht mal die neuen Koordinaten eines beliebig gedrehten Würfels selber zu berechnen), also suchte man etwas, was an Stelle des Weltkoordinatensystems verschoben werden könnte, und so einfach zu Handhaben war wie eine unrotierte Darstellung im Ursprung des Koordinatensystems. Wer mitgelesen hat wird es schon wissen... richtig! Es ist das Modellkoordinatensystem, von selbst darauf gekommen? Super!
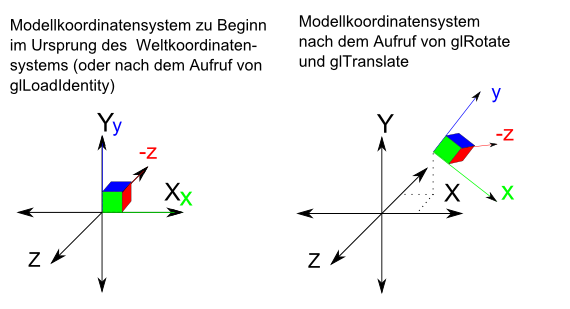
Das Modellkoordinatensystem liegt noch vor dem ersten Aufruf parallel zum Weltkoordinatensystem, also die Basisvektoren (x,y,z-Achsen) "zeigen" in die selbe Richtung und haben den selben Ursrpung (0-Punkt). Rufen wir nun eine OpenGL Funktion zur Veränderung (z.B. glTranlate, glRotate...) unseres Objektes auf, so ändern wir eigentlich nicht das Objekt sondern nur das Modellkoordinatensystem. Und nicht vergessen! Auch beim Programmieren definieren wir ja auch zuerst die Position (also das Modellkoordinatensystem) und dann zeichnen wird das Objekt, ist eigentlich nicht schwer zu verstehen oder? *g*
Ok, ok... ;) eine Beispielzeichnung:
Der Würfel in der Darstellung oben, ist eigentlich nicht notwendig und dient nur der Veranschaulichung.
Sollte es jemand also nach der folgenden Erläuterung nicht verstanden haben, kann er mich selbstverständlich persönlich per Mail zur "Rechenschaft" ziehen oder aber er wirft einen Blick in unser OpenGLWiki :)).
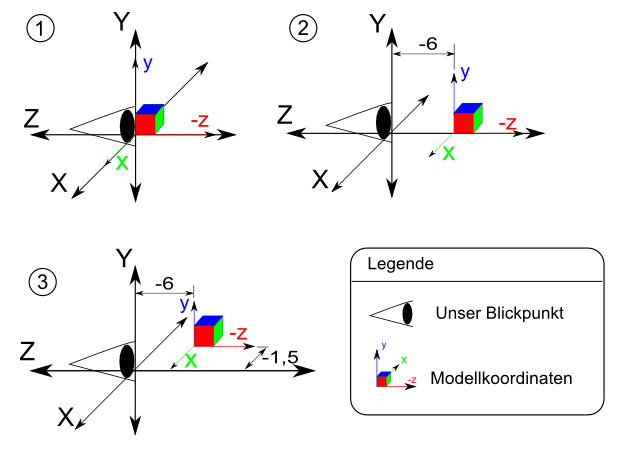
Wir setzen also zu Beginn unser Modellkoordinatensystem in den Mittelpunkt unseres Weltkoordinatensystems. Um oberes Beispiel aufzugreifen: Den Bildschirm. Dies geschieht mit dem Befehl glLoadIdentity und entspricht einem Reset der Modellmatrix. Theoretisch können wir nun an dieser Stelle etwas zeichnen. Dies würde allerdings dazu führen, dass das Objekt sehr groß oder gar nicht zu sehen ist, weil der Punkt (auch Augpunktkoordinate genannt) von dem aus wir unser Objekt betrachten sich genau an der Stelle befindet wo sich unser Objekt befindet, nämlich im Ursprung (vorausgesetzt wir Zeichnen ein Objekt um oder and den Ursprung, und das genau in der x/y-Ebene und nicht darüber oder darunter) . Gehen wir doch einmal 6 Einheiten nach hinten und 1,5 Einheiten nach links!
Eine kleine Beispielgrafik soll helfen:
Hierfür sollte man sich bewusst werden, dass wir in OpenGL praktisch an einen Stuhl gefesselt sind, d.h. wir können uns gar nicht bewegen. Das soll uns aber nicht davon abhalten. Wir brauchen ja nur die ganze Welt so zu bewegen, dass es für uns aussieht, als ob wir uns bewegen. Denn wenn sich alles außer uns nach links bewegt, haben wir den Eindruck, wir wären nach rechts gewandert, right?
Nun aber zu der Bewegung unseres ersten Objektes:
glTranslatef(0, 0,-6);
glTranslatef(-1.5,0,0);
Dies hat bewirkt, dass sich unser Zeichenstift 6 Einheiten nach hinten (negativer Bereicht der Y-Achse) und anschließend 1,5 Einheiten nach links (negativer Bereich der X-Achse) bewegt hat. Ich habe diesen Fall absichtlich in zwei Schritten gefasst, um es zu verdeutlichen. Sicherlich wäre es einfacher, alles mit nur einem Aufruf von glTranslate* zu machen:
glTranslatef(-1.5, 0,-6);
Man beachte, dass in diesem Fall die 6 Schritte nach hinten notwendig sind um ein bisschen Distanz zum Objekt zu bekommen und nicht direkt in ihm zu stehen!
Fertig! Schon haben wir dort unseren "Zeichenstift" positioniert, der nun auf weitere Zeichenkommandos von uns wartet. Das mag sicherlich alles ein wenig verwirrend klingen... probiert es am Besten aus und spielt mit den Parametern und erkennt, was gemeint ist :).
Von Sichtungen...
Die Büchse der Pandora
Nun sind wir aber auch alle scharf darauf, endlich etwas zu rendern und auf dem Bildschirm auszugeben. Dies geschieht z. B. mit folgenden Zeilen:
glBegin(GL_TRIANGLES);
glVertex3f(-1,-1, 0);
glVertex3f( 1,-1, 0);
glVertex3f( 0, 1, 0);
glEnd;
Wir erkennen hierbei eindeutig eine Art Block. Gerade wir Pascaler sollten diese ja lieben :->. Wir teilen OpenGL mit Hilfe von glBegin mit, dass wir ein Objekt zeichnen wollen. In diesem Fall übergeben wir den Parameter GL_TRIANGLE, der OpenGL angibt, dass folgende Punkte als ein Dreieck interpretiert werden sollen.
Anschließend folgt ein dreifacher Aufruf von glVertex3f. Jeder Aufruf erzeugt nun einen Punkt (Vertex) in unserem 3D-Raum. Da wir OpenGL bei glBegin mitgeteilt haben, dass diese Punkte zu einem Dreieck zusammengefügt werden sollen, wird das auch so getan ;).
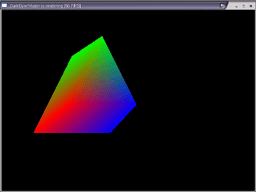
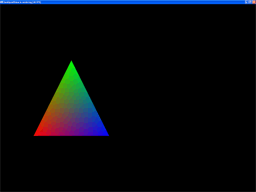
Wie wir auf dem Bild erkennen können, wurde unser Dreieck wie erwartet nach links verschoben abgebildet und auch mit einem leichten Abstand zur Kamera, nämlich 6 Einheiten entlang der Z-Achse.
Guter Stoff!
Nun... ein wenig trostlos sieht unser Dreieck nun doch aus, oder? Ich habe übrigens damals bei D3D rund eine Woche benötigt, bis ich ein schwarzes Dreieck hatte. Wir haben immerhin schon ein weißes... aber wir gehen nun einen Schritt weiter und werden das Dreieck schön bunt einfärben.
Bevor nun irgendjemand anfängt und Pixel für Pixel den Bildschirm nach zu pinseln oder gar sein PaintShop bereits offen hat, um die ersten Texturen zu erstellen, sei gestoppt! Es gibt für einfache Einfärbungen in OpenGL eine bessere Methode. Wir definieren einfach für jeden Eckpunkt eine Farbe und OpenGL wird dann sogar eigenständig die Farbverläufe dafür erstellen. Jeder der D3D kennt, wird diese Vorgehensweise bekannt vorkommen und er wird beginnen, verzweifelt nach dem FVF zu suchen, um es korrekt zu definieren... Wenn Ihr einen Vertex zeichnet, so rendert OpenGL diesen automatisch "weiß" (Ah huch! Deswegen ist unser Dreieck auch weiß???). Alles was wir nun machen müssen, ist OpenGL mitzuteilen, dass es eine andere Farbe einsetzen soll. Und zwar wird OpenGL diese Farbe für alle folgenden Eckpunkte nutzen, so lange bis von uns ein anderes Kommando kommt.
Der mysteriöse Befehl, um den ich nun schon die ganze Zeit herumschwafle ist glColor*:
// Alle folgenden Eckpunkte werden rot gefärbt
glColor3f(1,0,0);
Wobei jeder Parameter einen Farbwert repräsentiert und zwar nach dem Muster RGB. Es wird ein Wert zwischen 1 und 0 erwartet, wobei eine Eins "volle Farbsättigung" bedeutet. Das heißt in unserem Fall haben wir als Farbe "rot" gesetzt.
Und weil wir schließlich die Welt ein wenig bunter machen und nicht nur das weiße Dreieck rot färben wollten, werden wir nach jedem Eckpunkt eine neue Farbe setzen:
glBegin(GL_TRIANGLES);
glColor3f(1, 0, 0); glVertex3f(-1,-1, 0);
glColor3f(0, 0, 1); glVertex3f( 1,-1, 0);
glColor3f(0, 1, 0); glVertex3f( 0, 1, 0);
glEnd;
Und dies ist dann unser farbenfrohes Ergebnis. Beeindruckend, wenn man bedenkt, wie wenig Aufwand letztendlich dahinter steckt, oder?
Nachwort
Wer meine Tutorials kennt weiß, dass zum Abschluß noch immer ein wenig Geblubber von mir kommt (man beachte diese entzückende Wortwahl von meiner einer... hoffe, der Lektor findet es auch amüsant...). (Anm. des Lektors: Und wie!) Schauen wir doch mal stolz auf das zurück, was wir heute erreicht haben! Wir haben OpenGL initialisiert, ein erstes Dreieck auf den Bildschirm gezaubert und dieses in den Farbtopf gesteckt! Das solltet Ihr als ein historisches Ereignis ansehen. Als ich damals mit D3D angefangen habe, brauchte ich, um es mir selbst zu erarbeiten, ca. eine Woche (Das ist jetzt der Moment, in dem Ihr Eure Hände heben solltest und ein lautes "Call me God" aus Euch herauskommen sollte, so dass zumindest Eure unmittelbaren Mitmenschen denken, dass Ihr einen Dachschaden habt!!! Das gehört einfach mit dazu ^__- )
Wie immer solltet Ihr Euch nun hinsetzen und Euch ein wenig mit den Parametern vertraut machen. Speziell bei glTranslate* solltet Ihr ein wenig mit den Parametern experimentieren, damit Ihr seht, was es mit den Matrizen auf sich hat und wie diese funktionieren. Wenn Ihr dann auch denkt, dass Ihr damit vertraut seid, versucht ein wenig mit den einzelnen Vertexpositionen zu experimentieren und verändert diese. Wenn auch das klar ist, setzt Euch in die Ecke und warte sehnsüchtig auf mehr von uns :D! (Anm: Die "Ecke" ist nicht die Kneipe nebenan... :)
Im nächsten Kapitel werden wir dann Matrizen-Hardcore machen ... legt also schon mal Euer Aspirin parat, es wird witzig werden *grunz* :).
Und wie immer freuen wir uns sehr über Feedback. Schreibt uns doch einfach ein paar Worte in unser Feedback-Forum. Sagt, was Ihr gut und was hingegen Ihr als schlecht empfunden habt! Auch freuen wir uns immer über Ideen für weitere Tutorials, teilt uns also bitte Eure Ideen mit ;)!
Okay... ich wünsche Euch einen angenehmen Tag / Nacht!
Euer
Phobeus
Dateien
- Der aktuellste Beispiel-Quelltext befindet sich im DGLSDK 2006.1 für Windows
 und Linux
und Linux 
- Alter Delphi-API-Quelltext zum Tutorial

- Alter Delphi-VCL-Quelltext zum Tutorial

- Windows-Binary zum Tutorial

|
|
||
Vorhergehendes Tutorial: Tutorial Lektion 1 |
Nächstes Tutorial: Tutorial Lektion 3 |
|
|
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen. |
||