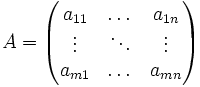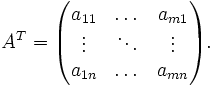Matrixtransposition: Unterschied zwischen den Versionen
Aus DGL Wiki
(Die Seite wurde neu angelegt: Bei der Matrix-Transposition werden die Spalten einer Matrix zu ihren Zeilen, z.B: wird {| |- align="center" | 1 || 2 || 3 || 4 || | |- align="center" | 5 || ...) |
K (hat „Matrix Transposition“ nach „Matrixtransposition“ verschoben: Ein Wort.) |
||
| (3 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Bei der [[Matrix]] | + | Bei der '''Transposition''' einer [[Matrix]] werden die Spalten einer Matrix zu ihren Zeilen. |
| − | |||
| − | + | <div align="center"> [[Bild:Matrix.png]]</div> | |
| − | + | wird durch Transposition zu | |
| − | + | <div align="center"> [[Bild:TransMatrix.png]]</div> | |
| − | |||
| − | |||
| − | |||
| − | + | Dies kommt einer Spiegelung an der Hauptdiagonalen der Matrix gleich. (Die Hauptdiagonale einer Matrix verläuft, vereinfacht gesagt, von oben links nach unten rechts. Mathematischer ausgedrückt gehören bei einer Matrix ''A'' alle Einträge A<sub>i,j</sub> mit i=j zur Hauptdiagonalen.) Im Bereich der 3D-Grafik ist diese Operation nützlich, da in einem häufigen Spezialfall die transponierte Matrix der [[Techniken zur Matrixinversion|inversen]] Matrix entspricht. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 22. Januar 2011, 19:52 Uhr
Bei der Transposition einer Matrix werden die Spalten einer Matrix zu ihren Zeilen.
wird durch Transposition zu
Dies kommt einer Spiegelung an der Hauptdiagonalen der Matrix gleich. (Die Hauptdiagonale einer Matrix verläuft, vereinfacht gesagt, von oben links nach unten rechts. Mathematischer ausgedrückt gehören bei einer Matrix A alle Einträge Ai,j mit i=j zur Hauptdiagonalen.) Im Bereich der 3D-Grafik ist diese Operation nützlich, da in einem häufigen Spezialfall die transponierte Matrix der inversen Matrix entspricht.