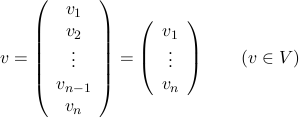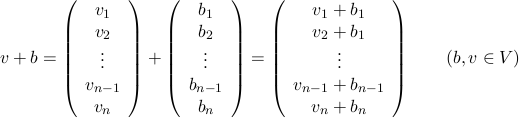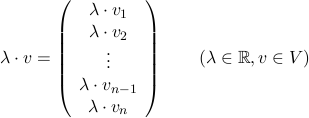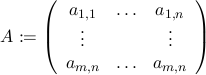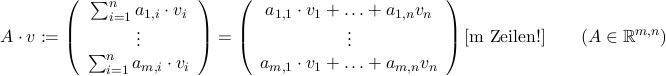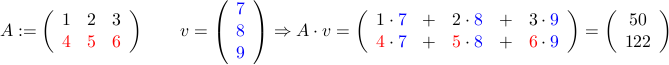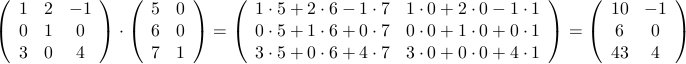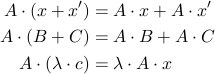Matrix: Unterschied zwischen den Versionen
K (Offline markiert zur Überarbeitung) |
(→Siehe auch) |
||
| (18 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | ==Matrix / Matrizen== | |
| − | == | + | ===Übersicht=== |
| + | Eine Matrix ist im wesentlichen nichts anderes als das, was man in der Programmierung als zweidimensionales Array kennt. Dabei beschreibt eine Matrix eine [http://de.wikipedia.org/wiki/Lineare_Abbildung lineare Abbildung], was als Information bei Rechnungen sehr wichtig ist. | ||
| − | + | '''Wichtig:''' Für den Einstieg in OpenGl ist ein tiefergehendes Verständnis von Matrizen noch nicht notwendig um bereits interessante Ergebnisse zu erzielen. Es genügt am Anfang zu wissen, dass man damit Verscheibungen, Drehungen und Streckungen beschreiben kann und dass die Reihenfolge der Befehle zum Manipulieren der Matrix wichtig ist. Wer also noch seine ersten Erfahrungen mit OpenGl macht, kann sich zuerst in unseren [[Tutorial|Tutorials]] informieren und erst anschließend hier wieder vorbeischauen. | |
| − | + | '''Anmerkung:''' Wir wollen mit den Definitionen hier nur soweit gehen, wie es für ein Verständnis von OpenGl Geometrie wichtig ist. In der Linearen Algebra werden einige der hier gegebenen Begriffe deutlich genauer und häufig auch abstrakter betrachtet. Dies würde jedoch unseren kleinen Rahmen deutlich sprengen. | |
| − | + | ===Definition=== | |
| − | < | + | Matrizen sind Abbildungen auf Vektorräumen ganzzahliger Dimension. Für alle weiteren Betrachtungen seien deshalb die Zahlen n,m und r aus dem Bereich {1,2,3,4,5,...}, also den natürlichen Zahlen ohne Null, fest vorgegeben. |
| + | |||
| + | ====R<sup>n</sup> Vektorräume==== | ||
| + | Um Matrizen definieren zu können, müssen wir zuerst Vektorräume definieren. Ein Vektorraum (V,*,+) ist eine Menge Vektoren V zusammen mit einer Skalar-Multiplikation * und einer Addition auf Vektoren, auf denen man vernünftig Vektorrechnung betreiben kann. | ||
| + | |||
| + | Hat man also zwei Vektoren v und w, so kann man diesen eindeutig einen Summevektor x zuordnen: | ||
| + | [[Bild:Vektor__summe.png|center]] | ||
| + | |||
| + | Außerdem kann man sie mit einem Skalar c aus den reelen Zahlen zu einem Vektor x' strecken: | ||
| + | [[Bild:Vektor__skalar.png|center]] | ||
| + | |||
| + | '''Beispiel''': Der Standardvektorraum R<sup>n</sup>: | ||
| + | Ein Vektor v aus dem R<sup>n</sup> besteht aus n reelen Zahlen ( seinen Komponenten v<sub>i</sub>), deren Reihenfolge wichtig ist und auch ''n-tupel'' genannt wird. Man kann also v auch in Form seiner Komponenten schreiben: | ||
| + | |||
| + | [[Bild:Vektorkomponenten.png|center]] | ||
| + | |||
| + | Häufig wird kein Unterschied dahingehend gemacht, ob der Vektor als Zeile oder als Spalte geschrieben wird. Bei der später definierten Matrixmultiplikation wird dies jedoch durchaus interessant, wir wollen uns also erstmal darauf beschränken, dass auch die Schreibweise | ||
| + | [[Bild:Vektortranspos.png|center]] | ||
| + | für unseren Vektor v eine legitime, als Text einfacher verfassbare Schreibweise darstellt. Bei der später definierten Multiplikation mit einer Matrix der Vektor aber immer als Spalte betrachtet wird. | ||
| + | |||
| + | Um unseren Vektorraum zu vervollständigen, brauchen wir nach Definition nun auch noch eine Addition und eine (Skalar-)Multiplikation. Die Addition geschieht komponentenweise. Hat man also einen zweiten Vektor b=(b<sub>1</sub>,...,b<sub>n</sub>), so ist die Addition definiert durch: | ||
| + | |||
| + | [[Bild:Vektoraddition.png|center]] | ||
| + | |||
| + | Die Multiplikation eines Vektors v mit einem reellen Faktor λ entspricht einer Streckung des Vektors um λ, was durch Multiplikation aller Komponenten von v mit λ erreicht wird: | ||
| + | |||
| + | [[Bild:Vektorskalarmultiplikation.png|center]] | ||
| + | |||
| + | Es ergeben sich die von den normalen reelen Zahlen bekannten Rechenregeln: | ||
| + | [[Bild:Vektorassoz.png|center]] | ||
| + | D.h. man kann Skalare einfach aus Klammern ausmultiplizieren oder wieder hineinziehen. Man beachte aber, dass die Multiplikation von Vektoren mit Vektoren nicht definiert ist (Siehe auch [[Vektorprodukt]], [[Standard Skalarprodukt]]). | ||
| + | |||
| + | Ist unser n gerade die Zahl 3 bzw. 2, so kann man durch den R<sup>n</sup> gerade den 3-Dimensionalen bzw. 2-Dimensionalen Anschauungsraum darstellen. Vektoren kann man dann sogar zeichnen und bekommt eine bildliche Vorstellung. Vektoren werden zu einer Darstellung von Pfeilen, die eine Richtung beschreiben oder ausgehend vom Nullpunkt des Koordinatensystems einen Punkt definieren: | ||
| + | |||
| + | [[Bild:Vektorvorstellung.jpg|center]] | ||
| + | |||
| + | ====Lineare Abbildungen auf dem R<sup>n</sup> in den R<sup>m</sup>==== | ||
| + | Weiter kann man Abbildungen f, die als Parameter Vektoren des R<sup>n</sup> annehmen und diese in den R<sup>m</sup> abbilden, definieren. Insbesondere kann man Abbildungen definieren, die linear sind, d.h. dass f folgende Eigenschaften erfüllt: | ||
| + | |||
| + | [[Bild:Lineare Abbildungen.png|center]] | ||
| + | |||
| + | und zwar für alle a,b aus R<sup>n</sup> und alle λ aus den reellen Zahlen R. Interessant ist, dass solche Abbildungen die Rechenregeln aus unserer Vektorraumdefinition erhalten. Sehr wichtig ist jedoch: Solche Abbildungen existieren. Die einfachste ist die, die alle Vektoren aus R<sup>n</sup> | ||
| + | auf die 0 abbildet ( die 0 ist der Vektor des R<sup>m</sup>, in dem alle Komponenten gleich 0 ist. ). Tatsächlich gibt es deutlich mehr dieser Abbildungen und alle lassen sich als Matrizen darstellen. Und umgekehrt: Mit Matrizen lassen sich alle lineare Abbildungen auf unseren Vektorräumen beschreiben. | ||
| + | |||
| + | ====mxn-Matrizen und ihre Anwendung auf Vektoren==== | ||
| + | Wie bereits angesprochen, sind Matrizen also 2 Dimensionale Felder aus rellen Zahlen: | ||
| + | |||
| + | [[Bild:mxnMatrix.png|center]] | ||
| + | |||
| + | Die a<sub>ij</sub> werden dann die Koeffizienten der Matrix genannt. Nun wollen wir das Anwenden der Matrix A aus R<sup>mxn</sup> auf einen Vektor x definieren: | ||
| + | |||
| + | [[Bild:mxnMatrixAnwendungaufx.png|center]] | ||
| + | |||
| + | Beispiel: | ||
| + | [[Bild:AnwendungsbeispielMatrizen.png|center]] | ||
| + | |||
| + | Am Bild erkennt man auch, warum die Matrix-Vektor Multiplikation ( " Anwendung " ) auch als Zeile mal Spalte bezeichnet wird, denn die Koeffizienten einer Zeile der Matrix werden der Reihe nach mit den Koeffizienten der "Spalte" des Vektors multipliziert. Dieses Verfahren kann man erweitern, indem man Vektoren als Matrizen interpretiert, die nur eine Spalte haben. Schreibt man mehrere Vektoren nebeneinander, kann man auf jede dieser Spalten die Matrix A darauf anwenden: | ||
| + | |||
| + | ====mxn-nxr-Matrix-Matrix Multiplikation==== | ||
| + | Man hat also eine mxn-Matrix A und eine nxr-Matrix B, die man Spaltenweise als Vektoren versteht: | ||
| + | |||
| + | [[Bild:zerlegungMatrixInEinzelvektoren.png|center]] | ||
| + | |||
| + | Bei der Multiplikation von A mit B, wird dann einfach A auf die Vektoren b<sub>i</sub> angewendet. | ||
| + | |||
| + | [[Bild:MatrixMatrixMultiplikation.png|center]] | ||
| + | |||
| + | Beispiel: | ||
| + | |||
| + | [[Bild:MatrixMatrixMultiplikationBeispiel.png|center]] | ||
| + | |||
| + | ====Eigenschaften==== | ||
| + | Diese Multiplikation hat eine Reihe von Eigenschaften: | ||
| + | * Versteht man die Matrizen A,B als lineare Abbildungen auf Vektoren x aus dem R<sup>n</sup> und y aus R<sup>r</sup>, also f(x) = A*x und g(y) = B*y und ist A eine mxn-Matrix, sowie B eine nxr Matrix, dann ist die Abbildung f(g(y)) eine Lineare Abbildung, die beschrieben ist durch | ||
| + | [[Bild:MatrixMatrixMultiplikationLinear.png|center]] | ||
| + | * Daraus ergibt sich, da schon die Definitions-Vektorräume verschieden sind, dass in den meisten Fällen '''nicht gilt''': '''A*B=B*A''' . Wer sich dies genauer überlegt, stellt fest, dass das 2. Produkt nur dann definiert ist, wenn A und B beides nxn-Matrizen sind. Aber selbst in diesem Fall ist es im Allgemeinen ein Unterschied, ob ich A*B oder B*A rechne (Das führt schließlich zu der Tatsache, dass man in OpenGL aufpassen muss, ob man zuerst rotiert und dann verschiebt (transliert) oder umgekehrt: Diese Operationen werden durch Matrizenmultiplikationen implementiert. Zu diesem Thema findet man am Ende des [[Tutorial_Matrix2]] einige Bilder.). | ||
| + | |||
| + | * Anderfalls gelten die Distributiv-, Assoziativ- und Kommutativgesetze: | ||
| + | [[Bild:MatrixMatrixMultiplikationLinear2.png|center]] | ||
| + | * Man nennt eine Gleichung A*x = b ein ''Lineares Gleichungssystem'', wenn A und b bekannt und x gesucht ist. Es interessiert dann, ob und - wenn ja - wie viele Lösungen es für x gibt. | ||
| + | |||
| + | ===Siehe Auch=== | ||
| + | Es gibt noch eine Menge weiterer Eigenschaften, und Funktionen, die in Bezug auf Matrizen höchst interessant sind: | ||
| + | |||
| + | [[Matrixtransposition]], [[Determinante]], [[Techniken zur Matrixinversion|Matrixinversion]], [[Gauss-Algorithmus]], [[Matrixmultiplikation|Matrizenmultiplikation]] | ||
| + | |||
| + | <!-- LaTeX-Quellcode | ||
| + | \documentclass[11pt]{article} | ||
| + | \newcommand {\bR}{{\mathbb R}} | ||
| + | \usepackage{amsmath,amsfonts} | ||
| + | \usepackage{xcolor} | ||
| + | \newcommand {\rd}{\color{red}} | ||
| + | \newcommand {\bl}{\color{blue}} | ||
| + | \begin{document} | ||
| + | \begin{align*} | ||
| + | x &= v + w\\ | ||
| + | x &= c \cdot v\\ | ||
| + | v &= \left ( \begin{array}{c} | ||
| + | v_1 \\ | ||
| + | v_2 \\ | ||
| + | \vdots \\ | ||
| + | v_{n-1} \\ | ||
| + | v_n | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | = | ||
| + | \left ( \begin{array}{c} | ||
| + | v_1 \\ | ||
| + | \vdots\\ | ||
| + | v_n | ||
| + | \end{array} | ||
| + | \right ) \qquad (v \in V)\\ | ||
| + | v^t &= (v_1, \ldots, v_n)\\ | ||
| + | v+b &= \left ( \begin{array}{c} | ||
| + | v_1 \\ | ||
| + | v_2 \\ | ||
| + | \vdots \\ | ||
| + | v_{n-1} \\ | ||
| + | v_n | ||
| + | \end{array} | ||
| + | \right ) + | ||
| + | \left ( \begin{array}{c} | ||
| + | b_1 \\ | ||
| + | b_2 \\ | ||
| + | \vdots \\ | ||
| + | b_{n-1} \\ | ||
| + | b_n | ||
| + | \end{array} | ||
| + | \right ) = | ||
| + | \left ( \begin{array}{c} | ||
| + | v_1 +b_1\\ | ||
| + | v_2 +b_1\\ | ||
| + | \vdots \\ | ||
| + | v_{n-1}+b_{n-1} \\ | ||
| + | v_n+b_n | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | \qquad (b,v \in V)\\ | ||
| + | \lambda \cdot v &= \left ( \begin{array}{c} | ||
| + | \lambda \cdot v_1 \\ | ||
| + | \lambda \cdot v_2 \\ | ||
| + | \vdots \\ | ||
| + | \lambda \cdot v_{n-1} \\ | ||
| + | \lambda \cdot v_n | ||
| + | \end{array} | ||
| + | \right ) \qquad (\lambda \in \bR, v\in V) \\ | ||
| + | \lambda \cdot (v+b) &= \lambda \cdot v + \lambda \cdot b \qquad (\lambda \in \bR, v,b \in V) | ||
| + | \end{align*} | ||
| + | |||
| + | \begin{align*} | ||
| + | 1) \; f(a+b) &= f(a) + f(b) &(a,b \in \bR^n, f(a),f(b) \in \bR^m)\\ | ||
| + | 2) \; f(\lambda \cdot a) &= \lambda \cdot f(a) &(a \in \bR^n, \lambda \in \bR, f(a) \in \bR^m) | ||
| + | \end{align*} | ||
| + | \begin{align*} | ||
| + | A &:= \left ( \begin{array}{ccc} | ||
| + | a_{1,1} & \ldots & a_ {1,n} \\ | ||
| + | \vdots & & \vdots \\ | ||
| + | a_{m,n} & \ldots & a_{m,n} | ||
| + | \end{array} | ||
| + | \right ) \\ | ||
| + | A\cdot v &:= | ||
| + | \left ( | ||
| + | \begin{array}{c} | ||
| + | \sum_{i=1}^{n}a_{1,i}\cdot v_i\\ | ||
| + | \vdots \\ | ||
| + | \sum_{i=1}^{n}a_{m,i}\cdot v_i | ||
| + | \end{array} | ||
| + | \right ) = | ||
| + | \left ( | ||
| + | \begin{array}{c} | ||
| + | a_{1,1}\cdot v_1 + \ldots + a_{1,n}v_n\\ | ||
| + | \vdots \\ | ||
| + | a_{m,1}\cdot v_1 + \ldots + a_{m,n}v_n | ||
| + | \end{array} | ||
| + | \right ) \mbox {[m Zeilen!]} \qquad (A \in \bR^{m,n}) | ||
| + | \end{align*} | ||
| + | \begin{align*} | ||
| + | A &:= \left ( | ||
| + | \begin{array}{ccc} | ||
| + | 1 & 2 & 3\\ | ||
| + | \rd 4 & \rd 5 & \rd 6 | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | \qquad | ||
| + | v = | ||
| + | \left ( | ||
| + | \begin{array}{c} | ||
| + | \bl 7\\ | ||
| + | \bl 8\\ | ||
| + | \bl 9 | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | \Rightarrow | ||
| + | A\cdot v = | ||
| + | \left ( | ||
| + | \begin{array}{ccccc} | ||
| + | 1\cdot {\bl 7} & +& 2 \cdot {\bl 8} &+& 3\cdot {\bl 9}\\ | ||
| + | {\rd 4}\cdot {\bl 7} & +& {\rd 5} \cdot {\bl 8} &+& {\rd 6}\cdot {\bl 9} | ||
| + | \end{array} | ||
| + | \right ) = | ||
| + | \left ( | ||
| + | \begin{array}{c} | ||
| + | 50\\ | ||
| + | 122 | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | \\ | ||
| + | & (n = 3, m = 2) | ||
| + | \\ | ||
| + | B &= \left ( \begin{array}{ccc} | ||
| + | \rd b_{1,1} & \ldots & \bl b_{1,r} \\ | ||
| + | \vdots & & \vdots \\ | ||
| + | \rd b_{n,r} & \ldots & \bl b_{n,r} | ||
| + | \end{array} | ||
| + | \right ) = ({\rd b_1}, \ldots , {\bl b_r})\\ | ||
| + | A \cdot B &:= (Ab_1, \ldots, Ab_r) \in \bR^{m,r} | ||
| + | \end{align*} | ||
| + | \begin{align*} | ||
| + | \left ( | ||
| + | \begin{array}{ccc} | ||
| + | 1 & 2 & -1\\ | ||
| + | 0 & 1 & 0 \\ | ||
| + | 3 & 0 & 4 | ||
| + | \end{array} | ||
| + | \right ) \cdot | ||
| + | \left ( | ||
| + | \begin{array}{cc} | ||
| + | 5 & 0\\ | ||
| + | 6 & 0 \\ | ||
| + | 7 & 1 | ||
| + | \end{array} | ||
| + | \right ) &= | ||
| + | \left ( | ||
| + | \begin{array}{cc} | ||
| + | 1\cdot5+2\cdot 6-1\cdot 7 & 1\cdot 0 + 2 \cdot 0 -1\cdot 1\\ | ||
| + | 0\cdot 5 + 1\cdot 6 + 0\cdot 7 & 0\cdot 0 + 1\cdot0+0\cdot 1 \\ | ||
| + | 3\cdot 5 + 0\cdot 6 + 4 \cdot 7 & 3\cdot 0 + 0\cdot 0 + 4\cdot 1 | ||
| + | \end{array} | ||
| + | \right ) = \left ( | ||
| + | \begin{array}{cc} | ||
| + | 10 & -1 \\ | ||
| + | 6 & 0 \\ | ||
| + | 43 & 4 | ||
| + | \end{array} | ||
| + | \right ) | ||
| + | \end{align*} | ||
| + | \begin {align*} | ||
| + | f(g(y)) &= A\cdot B \cdot y\\ | ||
| + | A\cdot(x+x') &= A\cdot x + A\cdot x' \\ | ||
| + | A\cdot(B+C) &= A \cdot B + A\cdot C \\ | ||
| + | A\cdot(\lambda\cdot c) &= \lambda \cdot A \cdot x | ||
| + | \end{align*} | ||
| + | \end{document} | ||
| + | --> | ||
| + | ==Matrizen in OpenGL== | ||
===Die drei OpenGL Matrizen=== | ===Die drei OpenGL Matrizen=== | ||
| + | In OpenGL gibt es drei 4x4-Matrizen welche alle mit Hilfe von [[glTranslate]], [[glScale]], [[glRotate]],[[glMultMatrix]],[[glLoadMatrix]] und [[glLoadIdentity]] bearbeitet werden können. Welche Matrix von diesen Funktionen beeinfusst wird, kann durch [[glMatrixMode]] gesteuert werden. | ||
| − | + | Die 3 Matrizen sind: | |
| − | |||
| − | |||
====GL_PERSPECTIVE==== | ====GL_PERSPECTIVE==== | ||
| Zeile 27: | Zeile 281: | ||
Beinhaltet Informationen wie Texturen dargestellt werden. | Beinhaltet Informationen wie Texturen dargestellt werden. | ||
| − | |||
Noch mehr Informationen zu den Matrizen und was sie bewirken gibts im [[Tutorial Matrix2]]. | Noch mehr Informationen zu den Matrizen und was sie bewirken gibts im [[Tutorial Matrix2]]. | ||
| − | |||
| − | |||
| − | |||
===Aufbau einer OpenGL-Matrix=== | ===Aufbau einer OpenGL-Matrix=== | ||
| − | Möchte man mit OpenGL an einer bestimmten Stelle etwas zeichnen, so kann man mit Hilfe von [[glTranslate]] und [[glRotate]] die Modelview-Matrix so manipulieren, dass etwa der mit [[glVertex]] übergebene Eckpunkt (0/0/0) im Weltkoordinaten System nicht mehr in der Mitte liegt. Alle Punkte erscheinen scheinbar in einen zweiten Koordinaten System welches etwas verdreht,vegrößert oder verrutsch liegen kann. | + | Möchte man mit OpenGL an einer bestimmten Stelle etwas zeichnen, so kann man mit Hilfe von [[glTranslate]] und [[glRotate]] die Modelview-Matrix so manipulieren, dass etwa der mit [[glVertex]] übergebene Eckpunkt (0/0/0) im Weltkoordinaten System nicht mehr in der Mitte liegt. Alle Punkte erscheinen scheinbar in einen zweiten Koordinaten System welches etwas verdreht, vegrößert oder verrutsch liegen kann. |
| − | Dieses zweite Koordinaten-System wird durch eine Matrix | + | Dieses zweite Koordinaten-System wird durch eine 4x4-Matrix, also einem zwei dimensionenlen Array mit vier Spalten und Zeilen, beschrieben. |
| − | Damit besser verstanden werden kann wie dies funktioniert, wird die Funktionsweise | + | Damit besser verstanden werden kann, wie dies funktioniert, wird die Funktionsweise anhand eines zwei dimensionalen Koordinaten System demonstiert. |
Möchte man in einem einfachen 2D Koordiaten-System den Punkt (X/Y) antragen, so hängt man X mal den Vektor der X-Achse aneinander, und Y mal den Vektor der Y-Achse. | Möchte man in einem einfachen 2D Koordiaten-System den Punkt (X/Y) antragen, so hängt man X mal den Vektor der X-Achse aneinander, und Y mal den Vektor der Y-Achse. | ||
| Zeile 50: | Zeile 300: | ||
[[Bild:KoordinatenSystemB.png]] | [[Bild:KoordinatenSystemB.png]] | ||
| + | Wie bereits bemerkt, müssten die Matrizen eigentlich 3x3-Matrizen sein, da sie ja auf dem 3D-Raum operieren sollen. Damit lassen sich jedoch keine Verschiebungen beschreiben, weswegen man bei der Übergabe von Vertexdaten mit [[glVertex]] im Hintergrund eine 4. Koordinate ''w'' neben (x,y,z) einführt. Diese hat, wenn nicht explizit über glVertex4x angegeben, den Wert 1. So lassen sich mit 3x3 Matrizen (aus denen jetzt durch Hinzunahme von ''w'', 4x4 Matrizen geworden sind) auch Verschiebungen beschreiben: | ||
| − | + | {| | |
| + | |- align="center" | ||
| + | | X || X || X || X || | | ||
| + | |- align="center" | ||
| + | | Y || Y || Y || Y || | | ||
| + | |- align="center" | ||
| + | | Z || Z || Z || Z || | | ||
| + | |- align="center" | ||
| + | | W || W || W || W || | | ||
| + | |} | ||
| + | So wirkt jede Zeile der OpenGl-Matrix auf genau die entsprechende | ||
| + | Koordinate des Vertex nach der Multiplikation mit einem Vertex (x,y,z,1). Ist die letzte Zeile der Matrix (0,0,0,1), hat also die Matrix die Form: | ||
| − | |||
{| | {| | ||
| − | |||
|- align="center" | |- align="center" | ||
| X || X || X || X || | | | X || X || X || X || | | ||
| Zeile 63: | Zeile 323: | ||
| Z || Z || Z || Z || | | | Z || Z || Z || Z || | | ||
|- align="center" | |- align="center" | ||
| − | | | + | | 0 || 0 || 0 || 1 || | |
|} | |} | ||
| + | Dann beschreibt die letzte Spalte der Matrix gerade die Verschiebung unseres Vertices, wie man mit der oben definierten Anwendung einer Matrix auf einen Vektor leicht überprüft. Am Ende wird die w-Koordinate, sofern sie 1 ist, wieder verworfen - was sie auch bleibt, denn die letzte Zeile der OpenGl Matrix ist gerade so gewählt, dass dies sichergestellt ist. Nur bei der endgültigen Darstellung auf den Monitor kommt der w-Koordinate noch eine weitere Bedeutung zu, weshalb Projektionsmatrizen ( erzeugt durch [[glOrtho]], [[glFrustum]], ... ) sich an Regel der letzten Zeile (0,0,0,1) nicht halten. | ||
| − | Folgendes Format könnte man | + | Folgendes Format könnte man nutzen, um eine Matrix mit [[glGetFloatv]] auszulesen oder mit [[glLoadMatrix]] zu setzen. |
| − | + | <syntaxhighlight lang="pascal">type | |
| − | + | TVektor = record | |
| − | + | X, Y, Z, W: glFloat; | |
| − | < | + | end; |
| + | TMatrix = array[(mat_XAchse, mat_YAchse, mat_ZAchse, mat_Position)] of TVektor; | ||
| + | PMatrix = ^TMatrix; | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | oder einfach | ||
| + | <syntaxhighlight lang="pascal">type | ||
| + | TMatrix = array[0..3, 0..3] of glFloat; | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | |||
| + | Man beachte dabei, dass OpenGL Matrizen '''Spaltenweise''' im Speicher ablegt sind. Siehe dazu auch: [[glMultMatrix]] | ||
| + | <!-- | ||
===Berechnungen=== | ===Berechnungen=== | ||
| Zeile 142: | Zeile 415: | ||
*[[glGet#GL_MATRIX_MODE|glGet]] mit GL_MATRIX_MODE | *[[glGet#GL_MATRIX_MODE|glGet]] mit GL_MATRIX_MODE | ||
<br> | <br> | ||
| + | --> | ||
| + | |||
| + | ===Zum leichteren Verständnis=== | ||
| + | ''Dieser Abschnitt ist nicht für fortgeschrittene 3D Entwickler gedacht, sollte aber Anfängern die immer noch nicht wissen, was Matrizen eigentlich in OpenGL machen einen leichteren Einblick verschaffen.'' | ||
| + | |||
| + | Um sich Matrizen in OpenGL leichter vorzustellen, kann man folgendes Bild benutzen: | ||
| + | |||
| + | * Die 3D-Welt ist in einer Art Glaskasten abgelegt in dem es keine Physik gibt (Dinge können in der Luft schweben u.ä.). | ||
| + | * Matrizen sind Maschinen/Greifarme. | ||
| + | * Matrizen sind die einzige Möglichkeit in den Glaskasten hinein zu greifen. | ||
| + | |||
| + | Wie wir weiter oben bereits gelernt haben sind Matrizen ja eigentlich Tabellen mit Zahlen. Diese Zahlen sind die Stellschrauben an unseren "Greifarmen". Mit diesen Stellschrauben können wir die Greifarme im Glaskasten positionieren. Durch den OpenGL-Befehl [[glMatrixMode]] können wir auswählen welchen der beiden Arme wir gerade steuern. | ||
| + | |||
| + | '''ModelView - Der Objektmanipulator''' | ||
| + | : Wird diese Matrix auf ein Objekt angewendet, ändert sich je nach Einstellung der Matrix dessen Position, Ausrichtung, Größe usw. (Man kann sogar den kompletten Glaskasten damit verschieben.) (Beispiel: Wirft man einen Würfel in eine Drehungsmatrix, kommt am Ende ein gedrehter Würfel raus.) | ||
| + | |||
| + | '''PerspectivMatrix - Die Kameralinse''' | ||
| + | : Diese Maschine ist nur für die Ausgabe zuständig. Man kann über die Stellschrauben einstellen, welche Art der Projektion (Parallel-, Perspektivisch-,...), und wie nah und wie weit Objekte maximal von der Kamera entfernt sein dürfen, um sichtbar zu sein. | ||
| + | |||
| + | Wer nun auf den Geschmack gekommen ist und mittels [[glLoadMatrix]] mal selber die Stellschrauben einer der beiden Matrizen ändern möchte, der sollte sich das sehr gute '''Mathe Script''' zum Thema '''Computer Geometrie''' einmal ansehen (siehe Links). Das eben vermittelte Bild mag zwar helfen. Die Theorie muss aber verstanden werden um damit arbeiten zu können. | ||
| + | |||
===Siehe auch=== | ===Siehe auch=== | ||
| − | [[glMatrixMode]], [[glGet]], [[glLoadIdentity]], [[glLoadMatrix]], [[glTranslate]], [[glRotate]], [[glScale]], [[Quaternion|Quaternionen]] | + | * [[glMatrixMode]], [[glGet]], [[glLoadIdentity]], [[glLoadMatrix]], [[glTranslate]], [[glRotate]], [[glScale]], |
| + | * [[Quaternion|Quaternionen]] | ||
| + | * [[Matrixmultiplikation|Matrix/Vektor-Multiplikationen]] - Auch SSE-beschleunigt. | ||
===Links=== | ===Links=== | ||
*[[Tutorial_Nachsitzen|Tutorial: Nachsitzen]] | *[[Tutorial_Nachsitzen|Tutorial: Nachsitzen]] | ||
*[http://www-user.tu-chemnitz.de/~pester/Lehre/CompGeo.pdf Recht umfangreiches, gut verständliches Script zum Thema "Computer Geometrie" (PDF)] | *[http://www-user.tu-chemnitz.de/~pester/Lehre/CompGeo.pdf Recht umfangreiches, gut verständliches Script zum Thema "Computer Geometrie" (PDF)] | ||
Aktuelle Version vom 5. Juli 2018, 22:08 Uhr
Inhaltsverzeichnis
Matrix / Matrizen
Übersicht
Eine Matrix ist im wesentlichen nichts anderes als das, was man in der Programmierung als zweidimensionales Array kennt. Dabei beschreibt eine Matrix eine lineare Abbildung, was als Information bei Rechnungen sehr wichtig ist.
Wichtig: Für den Einstieg in OpenGl ist ein tiefergehendes Verständnis von Matrizen noch nicht notwendig um bereits interessante Ergebnisse zu erzielen. Es genügt am Anfang zu wissen, dass man damit Verscheibungen, Drehungen und Streckungen beschreiben kann und dass die Reihenfolge der Befehle zum Manipulieren der Matrix wichtig ist. Wer also noch seine ersten Erfahrungen mit OpenGl macht, kann sich zuerst in unseren Tutorials informieren und erst anschließend hier wieder vorbeischauen.
Anmerkung: Wir wollen mit den Definitionen hier nur soweit gehen, wie es für ein Verständnis von OpenGl Geometrie wichtig ist. In der Linearen Algebra werden einige der hier gegebenen Begriffe deutlich genauer und häufig auch abstrakter betrachtet. Dies würde jedoch unseren kleinen Rahmen deutlich sprengen.
Definition
Matrizen sind Abbildungen auf Vektorräumen ganzzahliger Dimension. Für alle weiteren Betrachtungen seien deshalb die Zahlen n,m und r aus dem Bereich {1,2,3,4,5,...}, also den natürlichen Zahlen ohne Null, fest vorgegeben.
Rn Vektorräume
Um Matrizen definieren zu können, müssen wir zuerst Vektorräume definieren. Ein Vektorraum (V,*,+) ist eine Menge Vektoren V zusammen mit einer Skalar-Multiplikation * und einer Addition auf Vektoren, auf denen man vernünftig Vektorrechnung betreiben kann.
Hat man also zwei Vektoren v und w, so kann man diesen eindeutig einen Summevektor x zuordnen:
Außerdem kann man sie mit einem Skalar c aus den reelen Zahlen zu einem Vektor x' strecken:
Beispiel: Der Standardvektorraum Rn: Ein Vektor v aus dem Rn besteht aus n reelen Zahlen ( seinen Komponenten vi), deren Reihenfolge wichtig ist und auch n-tupel genannt wird. Man kann also v auch in Form seiner Komponenten schreiben:
Häufig wird kein Unterschied dahingehend gemacht, ob der Vektor als Zeile oder als Spalte geschrieben wird. Bei der später definierten Matrixmultiplikation wird dies jedoch durchaus interessant, wir wollen uns also erstmal darauf beschränken, dass auch die Schreibweise
für unseren Vektor v eine legitime, als Text einfacher verfassbare Schreibweise darstellt. Bei der später definierten Multiplikation mit einer Matrix der Vektor aber immer als Spalte betrachtet wird.
Um unseren Vektorraum zu vervollständigen, brauchen wir nach Definition nun auch noch eine Addition und eine (Skalar-)Multiplikation. Die Addition geschieht komponentenweise. Hat man also einen zweiten Vektor b=(b1,...,bn), so ist die Addition definiert durch:
Die Multiplikation eines Vektors v mit einem reellen Faktor λ entspricht einer Streckung des Vektors um λ, was durch Multiplikation aller Komponenten von v mit λ erreicht wird:
Es ergeben sich die von den normalen reelen Zahlen bekannten Rechenregeln:
D.h. man kann Skalare einfach aus Klammern ausmultiplizieren oder wieder hineinziehen. Man beachte aber, dass die Multiplikation von Vektoren mit Vektoren nicht definiert ist (Siehe auch Vektorprodukt, Standard Skalarprodukt).
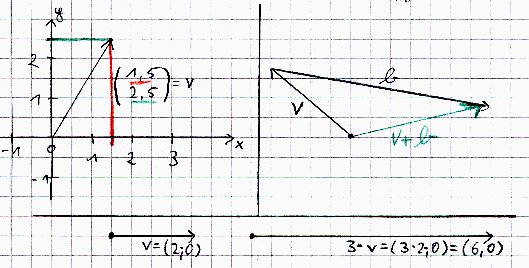
Ist unser n gerade die Zahl 3 bzw. 2, so kann man durch den Rn gerade den 3-Dimensionalen bzw. 2-Dimensionalen Anschauungsraum darstellen. Vektoren kann man dann sogar zeichnen und bekommt eine bildliche Vorstellung. Vektoren werden zu einer Darstellung von Pfeilen, die eine Richtung beschreiben oder ausgehend vom Nullpunkt des Koordinatensystems einen Punkt definieren:
Lineare Abbildungen auf dem Rn in den Rm
Weiter kann man Abbildungen f, die als Parameter Vektoren des Rn annehmen und diese in den Rm abbilden, definieren. Insbesondere kann man Abbildungen definieren, die linear sind, d.h. dass f folgende Eigenschaften erfüllt:
und zwar für alle a,b aus Rn und alle λ aus den reellen Zahlen R. Interessant ist, dass solche Abbildungen die Rechenregeln aus unserer Vektorraumdefinition erhalten. Sehr wichtig ist jedoch: Solche Abbildungen existieren. Die einfachste ist die, die alle Vektoren aus Rn auf die 0 abbildet ( die 0 ist der Vektor des Rm, in dem alle Komponenten gleich 0 ist. ). Tatsächlich gibt es deutlich mehr dieser Abbildungen und alle lassen sich als Matrizen darstellen. Und umgekehrt: Mit Matrizen lassen sich alle lineare Abbildungen auf unseren Vektorräumen beschreiben.
mxn-Matrizen und ihre Anwendung auf Vektoren
Wie bereits angesprochen, sind Matrizen also 2 Dimensionale Felder aus rellen Zahlen:
Die aij werden dann die Koeffizienten der Matrix genannt. Nun wollen wir das Anwenden der Matrix A aus Rmxn auf einen Vektor x definieren:
Beispiel:
Am Bild erkennt man auch, warum die Matrix-Vektor Multiplikation ( " Anwendung " ) auch als Zeile mal Spalte bezeichnet wird, denn die Koeffizienten einer Zeile der Matrix werden der Reihe nach mit den Koeffizienten der "Spalte" des Vektors multipliziert. Dieses Verfahren kann man erweitern, indem man Vektoren als Matrizen interpretiert, die nur eine Spalte haben. Schreibt man mehrere Vektoren nebeneinander, kann man auf jede dieser Spalten die Matrix A darauf anwenden:
mxn-nxr-Matrix-Matrix Multiplikation
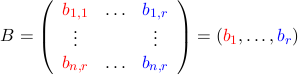
Man hat also eine mxn-Matrix A und eine nxr-Matrix B, die man Spaltenweise als Vektoren versteht:
Bei der Multiplikation von A mit B, wird dann einfach A auf die Vektoren bi angewendet.
Beispiel:
Eigenschaften
Diese Multiplikation hat eine Reihe von Eigenschaften:
- Versteht man die Matrizen A,B als lineare Abbildungen auf Vektoren x aus dem Rn und y aus Rr, also f(x) = A*x und g(y) = B*y und ist A eine mxn-Matrix, sowie B eine nxr Matrix, dann ist die Abbildung f(g(y)) eine Lineare Abbildung, die beschrieben ist durch
- Daraus ergibt sich, da schon die Definitions-Vektorräume verschieden sind, dass in den meisten Fällen nicht gilt: A*B=B*A . Wer sich dies genauer überlegt, stellt fest, dass das 2. Produkt nur dann definiert ist, wenn A und B beides nxn-Matrizen sind. Aber selbst in diesem Fall ist es im Allgemeinen ein Unterschied, ob ich A*B oder B*A rechne (Das führt schließlich zu der Tatsache, dass man in OpenGL aufpassen muss, ob man zuerst rotiert und dann verschiebt (transliert) oder umgekehrt: Diese Operationen werden durch Matrizenmultiplikationen implementiert. Zu diesem Thema findet man am Ende des Tutorial_Matrix2 einige Bilder.).
- Anderfalls gelten die Distributiv-, Assoziativ- und Kommutativgesetze:
- Man nennt eine Gleichung A*x = b ein Lineares Gleichungssystem, wenn A und b bekannt und x gesucht ist. Es interessiert dann, ob und - wenn ja - wie viele Lösungen es für x gibt.
Siehe Auch
Es gibt noch eine Menge weiterer Eigenschaften, und Funktionen, die in Bezug auf Matrizen höchst interessant sind:
Matrixtransposition, Determinante, Matrixinversion, Gauss-Algorithmus, Matrizenmultiplikation
Matrizen in OpenGL
Die drei OpenGL Matrizen
In OpenGL gibt es drei 4x4-Matrizen welche alle mit Hilfe von glTranslate, glScale, glRotate,glMultMatrix,glLoadMatrix und glLoadIdentity bearbeitet werden können. Welche Matrix von diesen Funktionen beeinfusst wird, kann durch glMatrixMode gesteuert werden.
Die 3 Matrizen sind:
GL_PERSPECTIVE
Sollte nur für die Festlegung der Perspektive genutzt werden.
GL_MODELVIEW
Legt Position und Größe des zu zeichnenden Primitiven fest
GL_TEXTURE
Beinhaltet Informationen wie Texturen dargestellt werden.
Noch mehr Informationen zu den Matrizen und was sie bewirken gibts im Tutorial Matrix2.
Aufbau einer OpenGL-Matrix
Möchte man mit OpenGL an einer bestimmten Stelle etwas zeichnen, so kann man mit Hilfe von glTranslate und glRotate die Modelview-Matrix so manipulieren, dass etwa der mit glVertex übergebene Eckpunkt (0/0/0) im Weltkoordinaten System nicht mehr in der Mitte liegt. Alle Punkte erscheinen scheinbar in einen zweiten Koordinaten System welches etwas verdreht, vegrößert oder verrutsch liegen kann.
Dieses zweite Koordinaten-System wird durch eine 4x4-Matrix, also einem zwei dimensionenlen Array mit vier Spalten und Zeilen, beschrieben.
Damit besser verstanden werden kann, wie dies funktioniert, wird die Funktionsweise anhand eines zwei dimensionalen Koordinaten System demonstiert.
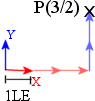
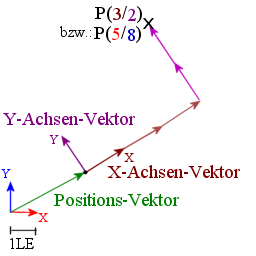
Möchte man in einem einfachen 2D Koordiaten-System den Punkt (X/Y) antragen, so hängt man X mal den Vektor der X-Achse aneinander, und Y mal den Vektor der Y-Achse.
Um die Lage und Größe eines Koordinatensystems zu beschreiben werden also einmal die Vektoren benötiget die 1 Längen Einheit meiner Achsen beschreiben, sowie ein Vektor der ihre Position in Anhängigkeit zum übergeordneten Koordinatensystems beschreibt.
Wie bereits bemerkt, müssten die Matrizen eigentlich 3x3-Matrizen sein, da sie ja auf dem 3D-Raum operieren sollen. Damit lassen sich jedoch keine Verschiebungen beschreiben, weswegen man bei der Übergabe von Vertexdaten mit glVertex im Hintergrund eine 4. Koordinate w neben (x,y,z) einführt. Diese hat, wenn nicht explizit über glVertex4x angegeben, den Wert 1. So lassen sich mit 3x3 Matrizen (aus denen jetzt durch Hinzunahme von w, 4x4 Matrizen geworden sind) auch Verschiebungen beschreiben:
| X | X | X | X | |
| Y | Y | Y | Y | |
| Z | Z | Z | Z | |
| W | W | W | W |
So wirkt jede Zeile der OpenGl-Matrix auf genau die entsprechende Koordinate des Vertex nach der Multiplikation mit einem Vertex (x,y,z,1). Ist die letzte Zeile der Matrix (0,0,0,1), hat also die Matrix die Form:
| X | X | X | X | |
| Y | Y | Y | Y | |
| Z | Z | Z | Z | |
| 0 | 0 | 0 | 1 |
Dann beschreibt die letzte Spalte der Matrix gerade die Verschiebung unseres Vertices, wie man mit der oben definierten Anwendung einer Matrix auf einen Vektor leicht überprüft. Am Ende wird die w-Koordinate, sofern sie 1 ist, wieder verworfen - was sie auch bleibt, denn die letzte Zeile der OpenGl Matrix ist gerade so gewählt, dass dies sichergestellt ist. Nur bei der endgültigen Darstellung auf den Monitor kommt der w-Koordinate noch eine weitere Bedeutung zu, weshalb Projektionsmatrizen ( erzeugt durch glOrtho, glFrustum, ... ) sich an Regel der letzten Zeile (0,0,0,1) nicht halten.
Folgendes Format könnte man nutzen, um eine Matrix mit glGetFloatv auszulesen oder mit glLoadMatrix zu setzen.
type
TVektor = record
X, Y, Z, W: glFloat;
end;
TMatrix = array[(mat_XAchse, mat_YAchse, mat_ZAchse, mat_Position)] of TVektor;
PMatrix = ^TMatrix;
oder einfach
type
TMatrix = array[0..3, 0..3] of glFloat;
Man beachte dabei, dass OpenGL Matrizen Spaltenweise im Speicher ablegt sind. Siehe dazu auch: glMultMatrix
Zum leichteren Verständnis
Dieser Abschnitt ist nicht für fortgeschrittene 3D Entwickler gedacht, sollte aber Anfängern die immer noch nicht wissen, was Matrizen eigentlich in OpenGL machen einen leichteren Einblick verschaffen.
Um sich Matrizen in OpenGL leichter vorzustellen, kann man folgendes Bild benutzen:
- Die 3D-Welt ist in einer Art Glaskasten abgelegt in dem es keine Physik gibt (Dinge können in der Luft schweben u.ä.).
- Matrizen sind Maschinen/Greifarme.
- Matrizen sind die einzige Möglichkeit in den Glaskasten hinein zu greifen.
Wie wir weiter oben bereits gelernt haben sind Matrizen ja eigentlich Tabellen mit Zahlen. Diese Zahlen sind die Stellschrauben an unseren "Greifarmen". Mit diesen Stellschrauben können wir die Greifarme im Glaskasten positionieren. Durch den OpenGL-Befehl glMatrixMode können wir auswählen welchen der beiden Arme wir gerade steuern.
ModelView - Der Objektmanipulator
- Wird diese Matrix auf ein Objekt angewendet, ändert sich je nach Einstellung der Matrix dessen Position, Ausrichtung, Größe usw. (Man kann sogar den kompletten Glaskasten damit verschieben.) (Beispiel: Wirft man einen Würfel in eine Drehungsmatrix, kommt am Ende ein gedrehter Würfel raus.)
PerspectivMatrix - Die Kameralinse
- Diese Maschine ist nur für die Ausgabe zuständig. Man kann über die Stellschrauben einstellen, welche Art der Projektion (Parallel-, Perspektivisch-,...), und wie nah und wie weit Objekte maximal von der Kamera entfernt sein dürfen, um sichtbar zu sein.
Wer nun auf den Geschmack gekommen ist und mittels glLoadMatrix mal selber die Stellschrauben einer der beiden Matrizen ändern möchte, der sollte sich das sehr gute Mathe Script zum Thema Computer Geometrie einmal ansehen (siehe Links). Das eben vermittelte Bild mag zwar helfen. Die Theorie muss aber verstanden werden um damit arbeiten zu können.
Siehe auch
- glMatrixMode, glGet, glLoadIdentity, glLoadMatrix, glTranslate, glRotate, glScale,
- Quaternionen
- Matrix/Vektor-Multiplikationen - Auch SSE-beschleunigt.