Tutorial Terrain3: Unterschied zwischen den Versionen
Flash (Diskussion | Beiträge) (Tutorial Übertragen (von Average Idiot)) |
K (Rechtschreibfehler ausgebessert) |
||
| (14 dazwischenliegende Versionen von 10 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=Continuous Level of Detail fur Heightmaps= | =Continuous Level of Detail fur Heightmaps= | ||
| − | == | + | ==Einführung== |
Hi, | Hi, | ||
| − | Ich habe in meinem ersten Heightmap Tutorial im Nachwort erzahlt, dass ich vielleicht ein Tutorial uber Level of Detail (LOD) fur Heightmaps schreibe. Ich will hiermit mein Versprechen | + | Ich habe in meinem ersten Heightmap Tutorial im Nachwort erzahlt, dass ich vielleicht ein Tutorial uber Level of Detail (LOD) fur Heightmaps schreibe. Ich will hiermit mein Versprechen einlösen, will euch aber auch gleich warnen, es ist nicht so leicht, wie man eigentlich denken könnte, denn viele Probleme stellen sich einem in den Weg, z.B. Cracks im [[Mesh]]. |
| − | |||
| − | |||
| + | Erkundigt man sich unter Spieleentwicklern nach LOD fur Heightmaps, wird man in den meisten Fallen wohl auf den Begriff ROAMing stosen. Dieser wird z.B. in einem meiner Lieblingsgames Tribes 2 verwendet. Mich hat dieser Algorithmus nicht wirklich angesprochen und ich habe weitergesucht. Nach einiger Zeit bin ich auf den Algorithmus aufmerksam geworden, der im Spiel Aquanox sein Konnen zeigt. Genauer gesagt bin ich über das [http://www.vterrain.org Virtual Terrain Project] darauf gestosen. Das Original Script von [http://www9.cs.fau.de/Persons/Roettger Stefan Röttger] findet sich direkt auf seiner Homepage unter Terrain Rendering: [http://wwwvis.informatik.uni-stuttgart.de/~roettger/data/Papers/TERRAIN.PDF Real-Time Generation of Continuous Levels of Detail for Height Fields] Ich kann euch wirklich warmstens empfehlen, dieses Script sich einmal genauer anzuschauen - sehr interessant. In diesem Tutorial werde ich das Schriftstück etwas genauer beleuchten und ein paar Hilfestellungen dazu geben, in der Hoffnung, dass ihr es mir gleich tut und diesen Algorithmus selbst einmal nachbaut. | ||
==Quadtree== | ==Quadtree== | ||
| − | Der | + | Der ganze Algorithmus basiert auf einem Quadtree. Dieser wird durch eine Boolean Matrix (für die Delpher, die immer noch nicht wissen, was eine Matrix ist: Wir reden uber ein 2 Dimensionales '''Array[0..n,0..n] of Boolean''') reprasentiert, so kann man sich eine Menge Pointer (und damit Speicherplatz) und viel Rechenarbeit sparen. Wir gehen davon aus, dass die Matrix eine Größe von (2n+1)x(2n+1) hat. Idealerweise hat die verwendete Heightmap die gleichen Ausmaße. Die Hauptnode sitzt in der Mitte der Matrix, die 4 Kinder... Bevor ich in Erklarungsnöte komme, hier einfach ein Bild, das den Sachverhalt verdeutlichen soll: |
| − | [[Bild:Tutorial_Terrain3_quadmatrix.gif]] | + | [[Bild:Tutorial_Terrain3_quadmatrix.gif|center]] |
| − | |||
| − | |||
| + | Ok, wir wissen nun, wie die Matrix aufgebaut ist, wie die Mutter Kind Verhältnisse des Quadtrees sind, etc., nur ist noch immer nicht klar, wozu diese Matrix. Wie bereits gesagt, handelt es sich um eine Boolean Matrix. Die Werte, die die Matrix annehmen kann, sind True oder False :-). Diese sagen aus, ob eine Node gesetzt ist und damit gezeichnet wird, oder eben nicht. Unsere Ziele sind also zum einen die Matrix rendern und zum andern die Matrix berechnen | ||
==Rendern der Heightmap== | ==Rendern der Heightmap== | ||
| − | Unsere Landschaft wird gerendert, indem wir den Quadtree rekursiv entlanggehen und immer wenn ein Endpunkt des Baums erreicht wird, wird ein kompletter oder | + | Unsere Landschaft wird gerendert, indem wir den Quadtree rekursiv entlanggehen und immer wenn ein Endpunkt des Baums erreicht wird, wird ein kompletter oder Teile eines Dreieck Fans gezeichnet. Diese Fans sind besonders gut dazu geeignet, ohne Löcher und Cracks im Mesh ein Heightfield darzustellen: |
[[Bild:Tutorial_Terrain3_setmatrix.gif]] | [[Bild:Tutorial_Terrain3_setmatrix.gif]] | ||
[[Bild:Tutorial_Terrain3_triangulation.gif]] | [[Bild:Tutorial_Terrain3_triangulation.gif]] | ||
| − | Das linke Bild stellt eine Beispiel Matrix dar, das rechte die dazu passende Triangulation. Ihr | + | Das linke Bild stellt eine Beispiel Matrix dar, das rechte die dazu passende Triangulation. Ihr könnt gerne nach Stellen suchen, an denen die Moglichkeit besteht, dass dort ein Crack ist. Ihr werdet keine finden. Zuerst wird einmal davon ausgegangen, dass der Levelunterschied im Quadtree zweier benachbarter Blocke niemals mehr als 1 beträgt. Diese Bedingung wird beim Berechnen der Matrix abgesichert, dazu später mehr. Das Zentrum eines Fans, ist immer auch das Zentrum eines Quadtree Blattes. Vier Vertieces bilden die Ecken des Blocks und weitere 4 bilden jeweils die Mittelpunkte der Seiten des Blattes: |
[[Bild:Tutorial_Terrain3_fan.gif]] | [[Bild:Tutorial_Terrain3_fan.gif]] | ||
| − | Es werden also | + | Es werden also höchstens 8 Dreiecke gezeichnet. Hat eine Seite keinen benachbarten Block gleichen Levels, so wird das Vertex in der Mitte der Seite einfach ubersprungen, was zur obigen Beispiel Triangulation fuhrt. |
==Erzeugen der Matrix== | ==Erzeugen der Matrix== | ||
| − | LOD besagt, dass | + | LOD besagt, dass Gegenstände in großer Entfernung mit einer niedrigeren Auflösung angezeigt werden, als nahe Objekte. Daneben werden auch bei größerer Entfernung bestimmte Teile eines Meshes mit höherer Auflösung angezeigt, deren Oberflache besonders uneben ist, wodurch die Bildqualitat stark erhoht wird. |
| − | === | + | ===Oberflächenfehler=== |
| − | Fehler? Fehler?!? Will ich euch jetzt verarschen, | + | Fehler? Fehler?!? Will ich euch jetzt verarschen, wäre doch dumm Fehler zu machen... Nein, die gemeinten Fehler besagen ausschließlich, wie verfälscht eine Stelle in der Landschaft aussehen wurde, wenn man beim Hinuntergehen des Baumes an der aktuellen Stelle aufhort und zu rendern beginnt. Je hoher dieser Wert, desto wichtiger ist es, den Baum noch tiefer hinabzuschreiten. |
| − | [[Bild:Tutorial_Terrain3_dhvalues.jpg]] | + | [[Bild:Tutorial_Terrain3_dhvalues.jpg|center]] |
Um diese '''d2''' genannten Werte fur ein Quadree Blatt zu erhalten, errechnet man zuerst die Erhebungsunterschiede an den Mitten der 4 Seiten und an den 2 Diagonalen(Achtung: das sind unterschiedliche Werte). Der '''d2''' Wert errechnet sich daraus so: | Um diese '''d2''' genannten Werte fur ein Quadree Blatt zu erhalten, errechnet man zuerst die Erhebungsunterschiede an den Mitten der 4 Seiten und an den 2 Diagonalen(Achtung: das sind unterschiedliche Werte). Der '''d2''' Wert errechnet sich daraus so: | ||
| Zeile 49: | Zeile 47: | ||
In Delphi konnte das ganze dann so aussehen: | In Delphi konnte das ganze dann so aussehen: | ||
| − | <pascal> | + | <source lang="pascal"> |
procedure CalcD2Value(X, Z, Size : Longint); | procedure CalcD2Value(X, Z, Size : Longint); | ||
var | var | ||
| Zeile 103: | Zeile 101: | ||
end | end | ||
end; (*CalcD2Values*) | end; (*CalcD2Values*) | ||
| − | ... | + | ... |
CalcD2Value((QuadTreeLength-1) div 2, (QuadTreeLength-1) div 2, | CalcD2Value((QuadTreeLength-1) div 2, (QuadTreeLength-1) div 2, | ||
(QuadTreeLength-1) div 2); | (QuadTreeLength-1) div 2); | ||
| − | ... | + | ... |
| − | </ | + | </source> |
| − | In diesem Beispiel steht '''Size''' immer fur die | + | In diesem Beispiel steht '''Size''' immer fur die Hälfte der Seitenlange einer Quadtreenode. Man denke hier am Besten an den Radius eines Kreises. Die '''d2''' Werte werden auf Bytegröße komprimiert, um wertvollen Speicher einzusparen. |
===Matrix erzeugen=== | ===Matrix erzeugen=== | ||
| − | Jetzt wollen wir uns daran machen, die | + | Jetzt wollen wir uns daran machen, die fürs Zeichnen unbedingt nötige Matrix zu erzeugen. Gehen wir einmal davon aus, dass die Matrix bereits sauber entleert ist und damit kein Node als gesetzt gilt. Wir laufen den Quadtree wieder rekursiv hinab und entscheiden an jeder Node nach folgender Formel, ob weiter unterteilt werden muss oder nicht: |
'''f=l/(d*C*max(c*d2, 1)''' | '''f=l/(d*C*max(c*d2, 1)''' | ||
| − | Ist der Wert von '''f''' kleiner 1, dann wird weiter unterteilt. Es gilt: '''C''' ist eine feste Konstante. Je | + | Ist der Wert von '''f''' kleiner 1, dann wird weiter unterteilt. Es gilt: '''C''' ist eine feste Konstante. Je höher sie ist, desto höher ist die Landschaft insgesamt aufgelost. '''l''' ist die Entfernung des Node Mittelpunkts zur Kamera und klein '''c''' kontrolliert die Auflösung in Bereichen, die einen hohen Oberflächenfehler aufweisen. |
===Schweizer Kase=== | ===Schweizer Kase=== | ||
| − | + | [[Bild:Tutorial_Terrain3_kaese.jpg|center]] | |
| − | Das bisherige Ergebnis ist doch mehr | + | Das bisherige Ergebnis ist doch mehr ernüchternd als erfreulich. Es sieht alles mehr nach Schweizer Kase aus. Viele Löcher, aber sonst nicht viel zu bieten. In einem Spiel kann man so ganz schnell dem Spieler den Spaß verderben, wir sollten also etwas dagegen unternehmen. |
| − | Um dieses Ziel zu erreichen, | + | Um dieses Ziel zu erreichen, müssen wir ganz einfach die '''d2''' Werte so verändern, dass Nebeneinanderliegende Blocke keinen Levelunterschied größer als 1 aufweisen (Bedingung für das Rendern der Matrix, siehe oben). Zuerst mussen also die '''d2''' Werte einmal berechnet worden sein. Nun gehen wir den Quadtree wieder soweit herunter, bis wir genau 1 level vor dem niedrigsten sind und setzen den '''d2''' Wert der Node neu: |
| − | <pascal> | + | <source lang="pascal"> |
| − | QuadMatrix[X,Z].D2Value := Max(QuadMatrix[X,Z].D2Value, (d2Werte der benachbarten Nodes ein Level tiefer) * K) | + | QuadMatrix[X,Z].D2Value := Max(QuadMatrix[X,Z].D2Value, |
| + | (d2Werte der benachbarten Nodes ein Level tiefer) * K) | ||
| + | K = C / (2 * (C - 1)); C groser 2 | ||
| + | </source> | ||
| − | |||
| + | <source lang="pascal"> | ||
procedure DoCrackAvoid(X, Z, Size, SizeToCheck : Longint); | procedure DoCrackAvoid(X, Z, Size, SizeToCheck : Longint); | ||
const | const | ||
| Zeile 168: | Zeile 169: | ||
end | end | ||
end; (*DoCrackAvoid*) | end; (*DoCrackAvoid*) | ||
| − | </ | + | </source> |
| − | Diesen Vorgang wiederholen wir, wobei wir immer ein Level niedriger gehen, bis wir schlieslich das Level 1 erreichen. Wenn wir nun unsere Matrix berechnen, ist unsere Bedingung | + | Diesen Vorgang wiederholen wir, wobei wir immer ein Level niedriger gehen, bis wir schlieslich das Level 1 erreichen. Wenn wir nun unsere Matrix berechnen, ist unsere Bedingung erfüllt und wir erhalten ein Mesh ohne Löcher: |
| − | [[Bild:Tutorial_Terrain3_result.jpg]] | + | [[Bild:Tutorial_Terrain3_result.jpg|center]] |
| − | [[Bild:Tutorial_Terrain3_wireframe.jpg]] | + | [[Bild:Tutorial_Terrain3_wireframe.jpg|center]] |
| − | Wer glaubt hier ein paar Locher finden zu | + | Wer glaubt hier ein paar Locher finden zu können liegt falsch. Die Stellen die schwarz erscheinen, werden durch das OpenGL Licht nur so unglucklich getroffen, dass sie fast schwarz erscheinen. Ist euer Monitor richtig eingestellt, sollte dagegen alles passen. Siehe dazu auch: [[Farbraum]]{{excIcon}}. Die "Kamera" befindet sich übrigens links unten im Bild, dort wo ein rotes Quad sichtbar ist. |
| + | '''Anmerkung:''' Nach Aussage von Stefan Röttger ist diese Methode um Löcher zu entfernen nicht optimal. Es genügt bei jedem Vater Knoten alle Kinder in die Berechnung einzubeziehen. Die Nachbarn müssen nicht einbezogen werden. Genaueres findet sich in diesem [http://www.delphigl.com/forum/viewtopic.php?p=48761#48761 Forumsbeitrag]. | ||
==Nachwort== | ==Nachwort== | ||
Wie gehts weiter? | Wie gehts weiter? | ||
| − | Um die ganze Sache nun noch ein | + | Um die ganze Sache nun noch ein bisschen weiter zu verbessern, sollte man überlegen, ob man die Landschaft nicht vielleicht texturiert. Hier bietet sich sicher das [[Tutorial_Terrain2|2. Heightmap Tutorial]] als guter Anfang an. Auch konnte man das "Popping" unterbinden, das auftritt, wenn man sich einer Stelle nähert und plötzlich ein paar neue Dreiecke angezeigt werden. Das ganze ist bekannt unter dem Begriff Geomorphing. |
| − | |||
| − | |||
| + | Delphic | ||
| + | == Dateien == | ||
| + | * {{ArchivLink|file=tut_terrainclod_delphi_vcl|text=Delphi-VCL-Quelltext zum Tutorial}} | ||
| + | * {{ArchivLink|file=tut_terrainclod_exe|text=Windows-Binary zum Tutorial}} | ||
| − | {{TUTORIAL_NAVIGATION|[[Tutorial_Terrain2]]| | + | {{TUTORIAL_NAVIGATION|[[Tutorial_Terrain2]]|[[Tutorial_Skyboxen]]}} |
[[Kategorie:Tutorial|Tutorial3]] | [[Kategorie:Tutorial|Tutorial3]] | ||
Aktuelle Version vom 25. September 2013, 15:31 Uhr
Inhaltsverzeichnis
Continuous Level of Detail fur Heightmaps
Einführung
Hi,
Ich habe in meinem ersten Heightmap Tutorial im Nachwort erzahlt, dass ich vielleicht ein Tutorial uber Level of Detail (LOD) fur Heightmaps schreibe. Ich will hiermit mein Versprechen einlösen, will euch aber auch gleich warnen, es ist nicht so leicht, wie man eigentlich denken könnte, denn viele Probleme stellen sich einem in den Weg, z.B. Cracks im Mesh.
Erkundigt man sich unter Spieleentwicklern nach LOD fur Heightmaps, wird man in den meisten Fallen wohl auf den Begriff ROAMing stosen. Dieser wird z.B. in einem meiner Lieblingsgames Tribes 2 verwendet. Mich hat dieser Algorithmus nicht wirklich angesprochen und ich habe weitergesucht. Nach einiger Zeit bin ich auf den Algorithmus aufmerksam geworden, der im Spiel Aquanox sein Konnen zeigt. Genauer gesagt bin ich über das Virtual Terrain Project darauf gestosen. Das Original Script von Stefan Röttger findet sich direkt auf seiner Homepage unter Terrain Rendering: Real-Time Generation of Continuous Levels of Detail for Height Fields Ich kann euch wirklich warmstens empfehlen, dieses Script sich einmal genauer anzuschauen - sehr interessant. In diesem Tutorial werde ich das Schriftstück etwas genauer beleuchten und ein paar Hilfestellungen dazu geben, in der Hoffnung, dass ihr es mir gleich tut und diesen Algorithmus selbst einmal nachbaut.
Quadtree
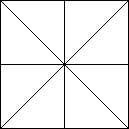
Der ganze Algorithmus basiert auf einem Quadtree. Dieser wird durch eine Boolean Matrix (für die Delpher, die immer noch nicht wissen, was eine Matrix ist: Wir reden uber ein 2 Dimensionales Array[0..n,0..n] of Boolean) reprasentiert, so kann man sich eine Menge Pointer (und damit Speicherplatz) und viel Rechenarbeit sparen. Wir gehen davon aus, dass die Matrix eine Größe von (2n+1)x(2n+1) hat. Idealerweise hat die verwendete Heightmap die gleichen Ausmaße. Die Hauptnode sitzt in der Mitte der Matrix, die 4 Kinder... Bevor ich in Erklarungsnöte komme, hier einfach ein Bild, das den Sachverhalt verdeutlichen soll:
Ok, wir wissen nun, wie die Matrix aufgebaut ist, wie die Mutter Kind Verhältnisse des Quadtrees sind, etc., nur ist noch immer nicht klar, wozu diese Matrix. Wie bereits gesagt, handelt es sich um eine Boolean Matrix. Die Werte, die die Matrix annehmen kann, sind True oder False :-). Diese sagen aus, ob eine Node gesetzt ist und damit gezeichnet wird, oder eben nicht. Unsere Ziele sind also zum einen die Matrix rendern und zum andern die Matrix berechnen
Rendern der Heightmap
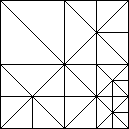
Unsere Landschaft wird gerendert, indem wir den Quadtree rekursiv entlanggehen und immer wenn ein Endpunkt des Baums erreicht wird, wird ein kompletter oder Teile eines Dreieck Fans gezeichnet. Diese Fans sind besonders gut dazu geeignet, ohne Löcher und Cracks im Mesh ein Heightfield darzustellen:
Das linke Bild stellt eine Beispiel Matrix dar, das rechte die dazu passende Triangulation. Ihr könnt gerne nach Stellen suchen, an denen die Moglichkeit besteht, dass dort ein Crack ist. Ihr werdet keine finden. Zuerst wird einmal davon ausgegangen, dass der Levelunterschied im Quadtree zweier benachbarter Blocke niemals mehr als 1 beträgt. Diese Bedingung wird beim Berechnen der Matrix abgesichert, dazu später mehr. Das Zentrum eines Fans, ist immer auch das Zentrum eines Quadtree Blattes. Vier Vertieces bilden die Ecken des Blocks und weitere 4 bilden jeweils die Mittelpunkte der Seiten des Blattes:
Es werden also höchstens 8 Dreiecke gezeichnet. Hat eine Seite keinen benachbarten Block gleichen Levels, so wird das Vertex in der Mitte der Seite einfach ubersprungen, was zur obigen Beispiel Triangulation fuhrt.
Erzeugen der Matrix
LOD besagt, dass Gegenstände in großer Entfernung mit einer niedrigeren Auflösung angezeigt werden, als nahe Objekte. Daneben werden auch bei größerer Entfernung bestimmte Teile eines Meshes mit höherer Auflösung angezeigt, deren Oberflache besonders uneben ist, wodurch die Bildqualitat stark erhoht wird.
Oberflächenfehler
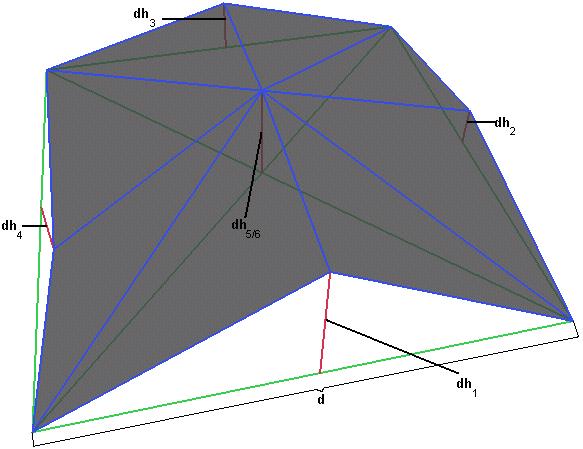
Fehler? Fehler?!? Will ich euch jetzt verarschen, wäre doch dumm Fehler zu machen... Nein, die gemeinten Fehler besagen ausschließlich, wie verfälscht eine Stelle in der Landschaft aussehen wurde, wenn man beim Hinuntergehen des Baumes an der aktuellen Stelle aufhort und zu rendern beginnt. Je hoher dieser Wert, desto wichtiger ist es, den Baum noch tiefer hinabzuschreiten.
Um diese d2 genannten Werte fur ein Quadree Blatt zu erhalten, errechnet man zuerst die Erhebungsunterschiede an den Mitten der 4 Seiten und an den 2 Diagonalen(Achtung: das sind unterschiedliche Werte). Der d2 Wert errechnet sich daraus so:
d2=(1/d)*maxi=1..6|dhi|
In Delphi konnte das ganze dann so aussehen:
procedure CalcD2Value(X, Z, Size : Longint);
var
HSize : LongInt; //Hälfte der eigenen Seitenlänge
I : LongInt;
EdgeHeights : Array[1..4] of Single; //Höhe der Ecken
ExpectedHeight : Single; //Erwartete höhe zw 2 Punkten
RealHeight : Single; //Tatsächliche Höhe
DHValues : Array[1..6] of Single; //DHWerte
const
//Ort der Ecken des Quads
Edges : Array[1..4] of Array[0..1] of ShortInt = ((+1, +1),(+1, -1),(-1,-1),(-1,+1));
//Jeweils die 2 Ecken, zwischen denen ein DHWert berechnet wird
DHLines : Array[1..6] of Array[0..1] of Byte =
((1,2),(2,3),(3,4),(4,1),(1,3),(2,4));
//Positionen der DHWerte selber
DHPositions : Array[1..6] of Array[0..1] of ShortInt =
((1,0),(0,-1),(-1,0),(0,1),(0,0),(0,0));
begin
//Höhen der 4 Ecken
for I := 1 to 4 do
EdgeHeights[I] := GetHeightMapHeight(X + Size * Edges[i,0],
Z + Size * Edges[i,1]);
//DHWerte berechen
for i := 1 to 6 do
begin
//Erwartete Höhe zwischen 2 Punkten
ExpectedHeight := (EdgeHeights[DHLines[i,0]] + EdgeHeights[DHLines[i,1]])/2;
//Tatsächlich vorliegende Höhe
RealHeight := GetHeightMapHeight(
X + DHPositions[i,0] * Size,
Z + DHPositions[i,1] * Size);
//DH Wert ist |absoluter Fehler|
DHValues[I] := Abs(ExpectedHeight - RealHeight)
end;
//D2Value finden und setzen
QuadMatrix[X,Z].D2Value := Trunc(1/(2*Size) * Max(DHValues));
//D2Values für die 4 Kinder
if Size > 1 then
begin
HSize := Size div 2;
CalcD2Value(X + HSize, Z + HSize, HSize);
CalcD2Value(X + HSize, Z - HSize, HSize);
CalcD2Value(X - HSize, Z + HSize, HSize);
CalcD2Value(X - HSize, Z - HSize, HSize)
end
end; (*CalcD2Values*)
...
CalcD2Value((QuadTreeLength-1) div 2, (QuadTreeLength-1) div 2,
(QuadTreeLength-1) div 2);
...
In diesem Beispiel steht Size immer fur die Hälfte der Seitenlange einer Quadtreenode. Man denke hier am Besten an den Radius eines Kreises. Die d2 Werte werden auf Bytegröße komprimiert, um wertvollen Speicher einzusparen.
Matrix erzeugen
Jetzt wollen wir uns daran machen, die fürs Zeichnen unbedingt nötige Matrix zu erzeugen. Gehen wir einmal davon aus, dass die Matrix bereits sauber entleert ist und damit kein Node als gesetzt gilt. Wir laufen den Quadtree wieder rekursiv hinab und entscheiden an jeder Node nach folgender Formel, ob weiter unterteilt werden muss oder nicht:
f=l/(d*C*max(c*d2, 1)
Ist der Wert von f kleiner 1, dann wird weiter unterteilt. Es gilt: C ist eine feste Konstante. Je höher sie ist, desto höher ist die Landschaft insgesamt aufgelost. l ist die Entfernung des Node Mittelpunkts zur Kamera und klein c kontrolliert die Auflösung in Bereichen, die einen hohen Oberflächenfehler aufweisen.
Schweizer Kase
Das bisherige Ergebnis ist doch mehr ernüchternd als erfreulich. Es sieht alles mehr nach Schweizer Kase aus. Viele Löcher, aber sonst nicht viel zu bieten. In einem Spiel kann man so ganz schnell dem Spieler den Spaß verderben, wir sollten also etwas dagegen unternehmen.
Um dieses Ziel zu erreichen, müssen wir ganz einfach die d2 Werte so verändern, dass Nebeneinanderliegende Blocke keinen Levelunterschied größer als 1 aufweisen (Bedingung für das Rendern der Matrix, siehe oben). Zuerst mussen also die d2 Werte einmal berechnet worden sein. Nun gehen wir den Quadtree wieder soweit herunter, bis wir genau 1 level vor dem niedrigsten sind und setzen den d2 Wert der Node neu:
QuadMatrix[X,Z].D2Value := Max(QuadMatrix[X,Z].D2Value,
(d2Werte der benachbarten Nodes ein Level tiefer) * K)
K = C / (2 * (C - 1)); C groser 2
procedure DoCrackAvoid(X, Z, Size, SizeToCheck : Longint);
const
Neighbours : Array[0..8] of Array[0..1] of ShortInt =
((+0,+0), (+3,+1),(+3,-1),(+1,-3),(-1,-3),(-3,-1),(-3,+1),(-1,+3),(+1,+3));
var
HSize : LongInt; //1/4 der Seitenlänge
I : LongInt;
D2Values : Array[0..8] of Byte;
begin
Assert(Size > 1);
//Der Baum wird rekursiv abgehandlet(nicht unbedingt die
//beste Idee. Wer Lust hat, darf sich gerne daran versuchen
//es einmal ohne Rekursivität zu probieren!)
HSize := Size div 2;
//Wir haben noch nicht das gewünschte Level erreicht
if Size > SizeToCheck then
begin
DoCrackAvoid(X + HSize, Z + HSize, HSize,SizeToCheck);
DoCrackAvoid(X + HSize, Z - HSize, HSize,SizeToCheck);
DoCrackAvoid(X - HSize, Z + HSize, HSize,SizeToCheck);
DoCrackAvoid(X - HSize, Z - HSize, HSize,SizeToCheck)
end
else
begin
Assert(SizeToCheck = Size);
D2Values[0] := QuadMatrix[X,Z].D2Value;
for i := 1 to 8 do
//Nachbarnodes holen....
D2Values[i] := GetNode(X + HSize * Neighbours[i][0],
Z + HSize * Neighbours[i][1]) * K;
QuadMatrix[X,Z].D2Value := MaxByte(D2Values)
end
end; (*DoCrackAvoid*)
Diesen Vorgang wiederholen wir, wobei wir immer ein Level niedriger gehen, bis wir schlieslich das Level 1 erreichen. Wenn wir nun unsere Matrix berechnen, ist unsere Bedingung erfüllt und wir erhalten ein Mesh ohne Löcher:
Wer glaubt hier ein paar Locher finden zu können liegt falsch. Die Stellen die schwarz erscheinen, werden durch das OpenGL Licht nur so unglucklich getroffen, dass sie fast schwarz erscheinen. Ist euer Monitor richtig eingestellt, sollte dagegen alles passen. Siehe dazu auch: Farbraum ![]() . Die "Kamera" befindet sich übrigens links unten im Bild, dort wo ein rotes Quad sichtbar ist.
. Die "Kamera" befindet sich übrigens links unten im Bild, dort wo ein rotes Quad sichtbar ist.
Anmerkung: Nach Aussage von Stefan Röttger ist diese Methode um Löcher zu entfernen nicht optimal. Es genügt bei jedem Vater Knoten alle Kinder in die Berechnung einzubeziehen. Die Nachbarn müssen nicht einbezogen werden. Genaueres findet sich in diesem Forumsbeitrag.
Nachwort
Wie gehts weiter? Um die ganze Sache nun noch ein bisschen weiter zu verbessern, sollte man überlegen, ob man die Landschaft nicht vielleicht texturiert. Hier bietet sich sicher das 2. Heightmap Tutorial als guter Anfang an. Auch konnte man das "Popping" unterbinden, das auftritt, wenn man sich einer Stelle nähert und plötzlich ein paar neue Dreiecke angezeigt werden. Das ganze ist bekannt unter dem Begriff Geomorphing.
Delphic
Dateien
|
|
||
Vorhergehendes Tutorial: Tutorial_Terrain2 |
Nächstes Tutorial: Tutorial_Skyboxen |
|
|
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen. |
||