Interpolation: Unterschied zwischen den Versionen
Lyr (Diskussion | Beiträge) K (→Kurven mit gegebenen Tangenten) |
Lyr (Diskussion | Beiträge) K (→Normalvektoren) |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 35: | Zeile 35: | ||
Somit erhalten wir die unsere Interpolationsgleichung: | Somit erhalten wir die unsere Interpolationsgleichung: | ||
I(x|y|z) = t * (2|-4|8) + (2|5|0) | I(x|y|z) = t * (2|-4|8) + (2|5|0) | ||
| + | |||
| + | Das Ergebnis sieht nun folgendermaßen aus: | ||
| + | |||
| + | [[Bild:InterpolationBsp1.png]] | ||
| + | |||
| + | ''2 dimensionale Version des obigen Beispieles. Die gegebenen Punkte sind somit A(2|5) und B(4|1). Diese Punkte sind in rot dargestellt. Die Gerade beinhaltet alle Punkte für die gegebene Formel mit t im Wertebereich [0|1]'' | ||
== Polynome höheren Grades == | == Polynome höheren Grades == | ||
| Zeile 103: | Zeile 109: | ||
Ix = -58.5 * t^3 + 90 * t^2 - 35.5 * t + 5 | Ix = -58.5 * t^3 + 90 * t^2 - 35.5 * t + 5 | ||
Iy = 22.5 * t^3 - 36 * t^2 + 12.5 * t + 3 | Iy = 22.5 * t^3 - 36 * t^2 + 12.5 * t + 3 | ||
| + | |||
| + | Das Ergebnis sieht nun folgendermaßen aus: | ||
| + | |||
| + | [[Bild:InterpolationBsp2.png]] | ||
| + | |||
| + | ''Oben angegebenes Beispiel grafisch dargestellt. Die Punkte P0 bis P3 sind rot dargestellt. Die Kurve beinhaltet alle Punkte der gegebenen Funktionen für ( Ix , Iy ) mit t im Wertebereich [0|1].'' | ||
=Kurven mit gegebenen Tangenten= | =Kurven mit gegebenen Tangenten= | ||
| Zeile 154: | Zeile 166: | ||
f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2 | f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2 | ||
Da die Dimensionen hier ebenfalls unabhängig sind, können Hermit-Kurven auf beliebig viele Dimensionen erweitert werden. | Da die Dimensionen hier ebenfalls unabhängig sind, können Hermit-Kurven auf beliebig viele Dimensionen erweitert werden. | ||
| + | |||
| + | Das Ergebnis sieht nun folgendermaßen aus: | ||
| + | |||
| + | [[Bild:InterpolationBsp3.PNG]] | ||
| + | |||
| + | ''Oben angegebenes Beispiel grafisch dargestellt. Die beiden Punkte sind rot dargestellt, die beiden Tangenten sind als blaue Geraden eingezeichnet. Die Kurve beinhaltet alle Punkte der gegebenen Funktionen für t im Wertebereich [0|1].'' | ||
=Tangenten von Kurven= | =Tangenten von Kurven= | ||
| Zeile 160: | Zeile 178: | ||
f'(t) = -6 * t^2 + 8 * t - t | f'(t) = -6 * t^2 + 8 * t - t | ||
Da die Dimensionen einer derartigen Kurve wie gesagt unabhängig voneinander behandelt werden können, kann man dadurch die Tangente in der entsprechenden Dimension erhalten. | Da die Dimensionen einer derartigen Kurve wie gesagt unabhängig voneinander behandelt werden können, kann man dadurch die Tangente in der entsprechenden Dimension erhalten. | ||
| + | |||
| + | = Interpolation mit anderen Funktionen = | ||
| + | Bisher wurden nur Interpolationen gezeigt, bei denen der t-Wert potenziert wurde. Es wurde immer ein Anfangspunkt verwendet, für den der t-Wert 0 sein sollte, und ein Endpunkt für den der t-Wert 1 sein sollte. Wir können natürlich jede beliebige Funktion für die Interpolation verwenden wo dies zutrifft. Wenn wir möchten können wir natürlich auch eine Funktion verwenden wo der Anfangspunkt bei t=X und der Endpunkt bei t=Y zu finden ist, denn eine derartige Funktion können wir wiederum umformen zu einer Funktion für die wir einen Anfangspunkt mit t=0 und einen Endpunkt mit t=1 haben. | ||
| + | |||
| + | Andere Funktionen werden meistens (nicht immer) bei nur 2 gegebenen Punkten verwendet. Hier wird meistens aus einem t-Wert im Bereich [0|1] ein neuer Wert u im Bereich [1|0] berechnet, welcher danach ähnlich wie bei der linearen Interpolation verwendet wird. Also: | ||
| + | u = f(t) | ||
| + | Interpolierter_Wert = I(t) = u * Startwert + (1-u) * Endwert | ||
| + | Wobei: | ||
| + | f(t) ... die Interpolationsfunktion, welche bei t=0 1 zurück liefert und bei t=1 0 ist. | ||
| + | Interpolierter_Wert ... das Ergebnis. | ||
| + | |||
| + | Mögliche andere Funktionen sind nun beispielsweise: | ||
| + | |||
| + | == Cosinus ähnliche Interpolation == | ||
| + | |||
| + | ===Cosinus Interpolation=== | ||
| + | Der Cosinus liefert Werte zwischen -1 und 1. Wir wollen einen eindeutigen y-Wert für y=Cos(t), somit verwenden wir nur t-Werte im Wertebereich von 0 bis 180 Grad (bzw. 0 bis Pi Radianten), denn bei t=181 Grad würden wir ja den selben Wert erhalten wie für t=179 Grad. | ||
| + | |||
| + | Der t-Wert wird für den Cosinus im Wertebereich [0|Pi] bzw. [0|180Grad] benötigt. Um nun einen t-Wert (wie zuvor) im Wertebereicheich von [0|1] verwenden zu können, multiplizieren wir ihn einfach mit Pi. Also verwenden wir einfach | ||
| + | t2 = t * Pi | ||
| + | bzw. das Ganze mit Grad: | ||
| + | t2 = t * 180 | ||
| + | |||
| + | Der Ausgabewert von Cosinus ist im Wertebereich [1|-1]. Um ihn auf den Wertebereich [1|0] zu bringen, müssen wir ihn transformieren. Dafür formen wir um: | ||
| + | f(t2) = Cos(t2) | ||
| + | g(t2) = f(t2)/2 + 1/2 = ( 1 + f(t2) ) / 2 = ( 1 + Cos(t2) ) / 2 | ||
| + | Und nun noch t2 durch t ersetzt: | ||
| + | g(t) = ( 1 + Cos(t*Pi) ) / 2 | ||
| + | bzw. das Ganze mit Grad: | ||
| + | g(t) = ( 1 + Cos(t*180) ) / 2 | ||
| + | |||
| + | Wir haben nun eine Formel die uns bei t=0 einen Wert von 1 liefert und bei t=1 einen Wert von 0. Dies können wir in unsere allgemeine Funktion einsetzen: | ||
| + | Interpolierter_Wert = I(t) = g(t) * Startwert + ( 1 - g(t) ) * Endwert | ||
| + | Und für g(t) eingesetzt: | ||
| + | Interpolierter_Wert = I(t) = ( (1+Cos(t*Pi))/2 ) * Startwert + ( 1 - (1+Cos(t*Pi))/2 ) * Endwert | ||
| + | bzw. das Ganze mit Grad: | ||
| + | Interpolierter_Wert = I(t) = ( (1+Cos(t*180))/2 ) * Startwert + ( 1 - (1+Cos(t*180))/2 ) * Endwert | ||
| + | |||
| + | Nun die Frage warum der ganze Aufwand, also warum nicht linear interpolieren? Um dies zu beantworten müssen wir die Steigungen dieser Funktion betrachten, wofür wir die Ableitung der Funktion berechnen: | ||
| + | I'(t) = 1/2 * Endwert * Pi * Sin( t * Pi ) - 1/2 * Startwert * Pi * Sin( t * Pi ) | ||
| + | Sieht kompliziert aus, aber wenn wir nun t=0 annehmen so erhalten wir für Sin( t * Pi ) ebenfalls 0. Wenn wir für t=1 annehmen so erhalten wir für Sin( t * Pi ) wiederum 0. Und dadurch erhalten wir an beiden Enden eine Steigung von 0. | ||
| + | |||
| + | Was können wir machen mit einer Funktion die an beiden Enden eine Steigung von 0 aufweist? Ganz einfach: wir können mehrere dieser Funktionen aneinander reihen, ohne das man einen übergang erkennt. Somit können wir sagen: | ||
| + | Bei t im Bereich [0|1] verwende als Startwert 3 und als Endwert 1 | ||
| + | Bei t im Bereich ]1|2] verwende als Startwert 1 und als Endwert 7 | ||
| + | Bei t im Bereich ]2|3] verwende als Startwert 7 und als Endwert 8 | ||
| + | Und wenn wir alle 3 Funktionen mit dem Wertebereich [0|1] verwenden (oder mathematisch ausgedrückt: I2(t) = I(t modulo 1) ), so erhalten wir eine Kurve ohne Kanten, oder um es etwas mathematischer auszudrücken: diese Funktion ist im Wertebereich ]0|3[ ableitbar, also in diesem Wertebereich auch stetig. | ||
| + | |||
| + | Und um die Ästhetik hinter diesen Formeln zu zeigen, ein Vergleich von linearer- zu cosinus-Interpolation: | ||
| + | |||
| + | [[Bild:Interpolation.png]] | ||
| + | |||
| + | === Quadratische Annäherung der Cosinus Interpolation === | ||
| + | Da die Berechnung des Cosinus eine etwas aufwändigere Angelegenheit ist, wünscht man sich hin und wieder eine Funktion die ähnlich aussieht und die gleichen Bedingungen (also eine Steigung von 0 an Start- und Endpunkt) erfüllt. Hierfür kann man 2 quadratische Funktionen verwenden die folgendes erfüllen müssen: | ||
| + | #Beide Kurven müssen einen gemeinsamen Punkt besitzen, also I1(t) = I2(t) für t im Wertebereich [0|1] | ||
| + | #An diesem Punkt müssen beide Kurven die selbe Steigung besitzen, also es existiert ein ( I1(X) = I2(X) wo auch gilt I1'(X) = I2'(X) ). | ||
| + | #Steigung (also Ableitung) bei t=0 und t=1 soll 0 sein | ||
| + | #Die Kurve sollte symmetrisch sein bezogen auf t=0.5, so das gilt: I1(t) = 1-I2(1-t). Somit muss gleichzeitig der Punkt wo gilt I1(t) = I2(t) bei 0.5 liegen. | ||
| + | |||
| + | Wir können uns nun aus der ersten und dritten Bedinung einfach die beiden Formeln herleiten, aber um es kurz zu machen: | ||
| + | Wenn t <= 0.5 dann I1(t) = -2*t^2 + 1 | ||
| + | Wenn t > 0.5 dann I2(t) = 2*t^2 - 4*t + 2 = 2 * (1-t)^2 | ||
| + | Nun zeigen wir, dass die oben angegebenen Bedingungen erfüllt sind: | ||
| + | #I1(0.5) = -2*0.5^2 + 1 = 0.5; I2(0.5) = 2 * (1-0.5)^2) = 0.5 | ||
| + | #I1'(t) = -4t, I1'(0.5) = -2; I2'(t) = 4*t - 4, I2'(0.5) = -2 | ||
| + | #I1'(0) = -4*0 = 0; I2'(1) = 4*1 - 4) = 0 | ||
| + | #I1(t) = 1-I2(1-t) '''=>''' -2*t^2 + 1 = 1 - (2*(1-t)^2 - 4*(1-t) + 2) '''=>''' -2*t^2 + 1 = 1 - (2 - 4*t + 2*t^2 - 4 + 4*t + 2) '''=>''' -2*t^2 + 1 = -2*t^2 + 1 | ||
| + | |||
| + | === Cosinus ähnliche Interpolation durch Polynominterpolation === | ||
| + | Wenn wir eine Polynominterpolation mit den beiden Endtangenten 0 berechnen wollen, so verwenden wir eine Hermite Kurve. Hierbei verwenden wir die Werte: | ||
| + | 1 ... Startpunkt | ||
| + | 0 ... Endpunkt | ||
| + | 0 ... Steigung bei Startpunkt | ||
| + | 0 ... Steigung bei Endpunkt | ||
| + | Mit der unter Hermit Kurven angegebenen Matrix M^-1 können wir uns nun die dazugehörige Funktion berechnen und erhalten: | ||
| + | I(t) = 2*t^3 - 3*t^2 + 1 | ||
| + | Die ersten beiden Bedingungen von vorher sind automatisch erfüllt, da es sich nur um eine Funktion handelt. Für die 3. und 4. Bedingung lässt sich ebenfalls verhältnismäßig einfach zeigen das sie erfüllt sind. | ||
| + | |||
| + | === Vergleich der Cosinus ähnlichen Interpolationsarten === | ||
| + | Und zu guter letzt hier noch die grafische Veranschaulichung der etwas zahlenbeladenen Funktionen. | ||
| + | |||
| + | [[Bild:InterpolationCosAnnaeherung.png]] | ||
| + | |||
| + | ''Die 3 Cosinus ähnlichen Funktionen graphisch dargestellt: | ||
| + | *Grün: Cos-Interpolation | ||
| + | *Rot: Polynom-Interpolation | ||
| + | *Blau: Quadratische Annäherung'' | ||
=Interpolierte Flächen= | =Interpolierte Flächen= | ||
| Zeile 165: | Zeile 270: | ||
==Normalvektoren== | ==Normalvektoren== | ||
| − | Besitzt man Flächen und berechnet sie nach dem gegebenen Schema, so berechnet man sich zuerst auch mehrere Kurven von denen man die Tangenten berechnen kann. Interpoliert man nun diese Tangenten mit der gleichen Kurvenfunktion wie die resultierenden Punkte, und berechnet sich aus der resultierenden Kurvenfunktion ebenfalls die Tangente, so erhält man 2 Tangenten. Aus diesen beiden Tangenten kann nun mit einem Kreuzprodukt ein Normalvektor errechnet werden. | + | Besitzt man Flächen und berechnet sie nach dem gegebenen Schema, so berechnet man sich zuerst auch mehrere Kurven von denen man die Tangenten berechnen kann. Interpoliert man nun diese Tangenten mit der gleichen Kurvenfunktion wie die resultierenden Punkte, und berechnet sich aus der resultierenden Kurvenfunktion ebenfalls die Tangente, so erhält man 2 Tangenten. Aus diesen beiden Tangenten kann nun mit einem Kreuzprodukt ein Normalvektor errechnet werden. |
| − | |||
=Kurvenlängen-Interpolation= | =Kurvenlängen-Interpolation= | ||
| − | Es könnte erwünscht sein (beispielsweise für Kamerafahrten, Keyframe Interpolationen jeglicher Art oder auch bei der Interpolation von Positionsangaben die man beispielsweise über ein Netzwerk erhält), dass man über keine fixe Achse t interpolieren möchte, sondern über die Kurvenlänge. | + | Es könnte erwünscht sein (beispielsweise für Kamerafahrten, Keyframe Interpolationen jeglicher Art oder auch bei der Interpolation von Positionsangaben die man beispielsweise über ein Netzwerk erhält), dass man über keine fixe Achse t interpolieren möchte, sondern über die Kurvenlänge. |
| − | + | ||
| − | + | Bei den typischen physikalischen Beispielen besitzt man meist eine Geschwindigkeit welche durch Beschleunigung verändert wird. Also wenn man einen Ball senkrecht hoch wirft, so gibt es einen Punkt an dem er komplett stehen bleibt. Für diese Art von physikalischen Berechnungen wird man also kaum eine Kurvenlängen-Interpolation benötigen. | |
| − | ' | + | |
| + | Wenn man jedoch sehr langsame Geschwindigkeiten besitzt, also beispielsweise zu fuß geht, so haben wir eine nahezu konstante Gehgeschwindigkeit, egal ob wir eine Kurve gehen oder nicht. Wenn wir noch weiter gehen und auf einer Straße oder einer Rennstrecke alle 100 Meter ein Längenangabenschild hin stellen möchten, so ist uns Beschleunigung und auch die Geschwindigkeit vollkommen egal. Wir hätten also am liebsten eine Funktion P(s), welche uns den Punkt der Kurve für für Kilometer (oder Meter) s liefert. | ||
| + | |||
| + | ==Der eindimensionale Fall== | ||
| + | Dieser Teil soll lediglich als Erklärung dienen, besitzt in der Praxis aber kaum Relevanz. | ||
| + | |||
| + | Im Eindimensionalen Fall kann man sich dies noch sehr gut veranschaulichen. Wenn ich eine gerade Strecke besitze und meine 1D-Koordinaten kenne, so kann ich ganz einfach sagen: zum Zeitpunkt t bin ich Betrag( f(t) - f(t0) ) Meter (allg. Einheiten) gegangen. Interessant wir es noch mal wenn ich die Richtung ändere, also wenn ich bei Kilometer 4 merke das ich etwas zu Hause vergessen habe, noch einmal umdrehe und dann weiter fahre. In diesem Fall kann ich nicht sagen: ich befinde mich an Position 10 Kilometer entfernt => ich bin 10 Kilometer gegangen, sondern in Wirklichkeit habe ich noch zusätzlich 8 Kilometer umweg hinter mir. | ||
| + | |||
| + | Dieses simple beispiel mathematisch ausgedrückt: | ||
| + | |||
| + | wenn f(t) monoton steigend oder monoton fallend ist: Kurvenlänge(t) = | f(t) - f(t0) | | ||
| + | Sonnst: Kurvenlänge = Integral[t0 bis t]( f'(t) ) | ||
| + | Beim Integrieren müssen wir nun aufpassen, ob unsere Stammfunktion 0-Stellen besitzt. Bei jeder solchen 0-Stelle Zx zerteilen wir die Wertebereiche: | ||
| + | W = [t0, Z1, Z2, Z3, ..., Zn, t] | ||
| + | |||
| + | Kurvenlänge(t) = Summe[ n=1 bis Elemente von W ]( Integral[W[n-1] bis W[n]]( f'(t) ) | ||
| + | Da wir nun in der Stammfunktion alle 0-Stellen berücksichtigt haben können wir das Integral "kürzen", also | ||
| + | Kurvenlänge(t) = Summe[ n=1 bis Elemente von W ]( | f(w[n]) - f(w[n-1]) | ) | ||
| + | |||
| + | Das Integral macht hier also nichts anderes als Richtungswechsel zu erkennen, denn bei einem Richtungswechsel in 1D ändert sich das Vorzeichen der Ableitung einer Funktion, und für jeden Vorzeichenwechsel muss es auch einen 0-Punkt geben wenn es sich um eine stetige Funktion handelt. | ||
| + | |||
| + | Wir kennen nun also den Weg den wir zu einem bestimmten Zeitpunkt zurückgelegt haben. Wir wollen jedoch den Zeitpunkt wissen an dem wir eine bestimmte Weglänge zurückgelegt haben, um die Funktion f(t) durch f(t(s)) = g(s) wodurch g(s) eine Funktion ist wo wir die Position für einen bestimmte Kurvenlänge erhalten. | ||
| + | |||
| + | Wir müssen also ein t finden für das gilt | ||
| + | Kurvenlänge(t) = s | ||
| + | und können danach dieses t in unsere Ursprüngliche Kurvengleichung einsetzen. | ||
| + | |||
| + | Und nun mit voller Wucht: warum bringt uns das alles ganz und gar nichts? | ||
| + | Wenn wir eine Eindimensionale "Kurve" besitzen und wir wollen diese über die Kurvenlänge parametrisieren, so sagen wir schlicht und ergreifend: | ||
| + | x = x0 +/- s | ||
| + | wenn wir nicht mehrere Fälle besitzen. Wenn wir Fallunterscheidungen bekommen, so gibt es (wie im mehrdimensionalen Fall noch verdeutlicht wird) natürlich auch Methoden mit denen wir diese Fallunterscheidungen umgehen können (namentlich: numerische Integration). Dennoch ist die Funktion wohl in nahezu allen Fällen einfacher mit derartigen Fallunterscheidungen zu berechnen. | ||
| + | |||
| + | ===Beispiel=== | ||
| + | Ein Beispiel noch am Rande, wie man unschwer erahnen kann, gibt es eher wenig alltäglichere Beispiele die nicht zu trivial und von Interesse wären: | ||
| + | |||
| + | Wir besitzen eine gedämpfte Schwingung mit der Formel | ||
| + | f(t) = e^(-t) * sin(t) | ||
| + | und möchten aus unerfindlichen Gründen wissen wo sich der schwingende Körper befindet wenn er den Weg s zurückgelegt hat. | ||
| + | |||
| + | Wir berechnen uns die Ableitung | ||
| + | f'(t) = e^(-t) * cos(t) - e^(-t) * sin(t) | ||
| + | und nun die 0-Stellen, also | ||
| + | f'(t) = 0 | ||
| + | davon gibt es aber natürlich jede Menge ... aber wir begnügen und mit den ersten 3: | ||
| + | f'(PI/4) = 0 | f(PI/4) ~= 0.322 | ||
| + | f'(~3.927) = 0 | f(3.927) ~= -0.014 | ||
| + | f'(~7.069) = 0 | f(7.069) ~= 0.0006 | ||
| + | Da der Startpunkt (t=0) natürlich auch bei 0 liegt, erhalten wir also jetzt für unsere Position in Abhängigkeit der Weglänge s: | ||
| + | g(s) = s für s im Bereich [0,0.322] | ||
| + | g(s) = 2*0.322-s für s im Bereich ]0.322|0.658] wobei 0.658 = 0.322 + | 0.322-0.014 | | ||
| + | g(s) = s-2*0.322-2*0.014 für s im Bereich ]0.658|0.6585] wobei 0.6586 = 0.322 + | 0.322 - (-0.014) | + | -0.014 - 0.0006 | | ||
| + | |||
| + | ==Kurven in höheren Dimensionen== | ||
| + | Im allgemeinen Fall kann eine Kurve in einer bestimmten Dimension als Vektor von Funktionen dargestellt werden: | ||
| + | | x(t) | | ||
| + | P(t) = | y(t) | | ||
| + | | z(t) | | ||
| + | | ... | | ||
| + | wir können die Tangente berechnen indem wir in jeder Dimensionen die Funktion ableiten: | ||
| + | | x'(t) | | ||
| + | T(t) = | y'(t) | | ||
| + | | z'(t) | | ||
| + | | ... | | ||
| + | und natürlich handelt es sich nun nicht um irgendeine Tangente, sondern um die Tangente welche auch die Änderungsgeschwindigkeit der Kurve abhängig von t beschreibt. Wir können die Länge dieser Tangente also als Geschwindigkeit der Kurve betrachten. Die Länge eines Vektors ist ein skalarer Wert, also erhalten wir für die Geschwindigkeit zu einem Zeitpunkt t die Funktion: | ||
| + | Geschwindigkeit(t) = | T(t) | | ||
| + | Der Betrag der Tangente wir nun folgendermaßen gebildet: | ||
| + | Geschwindigkeit(t) = Wurzel( x'(t)^2 + y'(t)^2 + z'(t)^2 + ... ) | ||
| + | Nun besitzen wir eine Funktion für die Geschwindigkeit der Kurve welche uns integriert die Länge der Kurve bis zum Zeitpunkt t angibt. Im Gegensatz zum eindimensionalen Fall (wo dies eher wenig Sinn hatte) quadrieren wir hier jeden verwendeten Wert, wodurch diese Funktion niemals < 0 werden kann, somit müssen wir beim integrieren auch nicht auf 0-Stellen aufpassen. | ||
| + | |||
| + | Wir Integrieren nun: | ||
| + | Kurvenlänge(t) = Integral[t0 bis t]( Geschwindigkeit(t) ) | ||
| + | |||
| + | Und hier stoßen wir an einen unangenehmen Punkt. Nehmen wir ein "einfaches" Polynom für x(t), y(t) und z(t). An einem Integral wie aus unserem Polynom-Beispiel: | ||
| + | Integral[t0 bis t]( Wurzel( (-58.5*t^3 + 90*t^2 - 35.5*t + 5)^2 + (22.5*t^3 - 36*t^2 + 12.5*t + 3)^2 ) ) | ||
| + | scheitern sogar gute Mathematik-Bibliotheken, und von normalsterblichen Menschen ganz zu schweigen. | ||
| + | |||
| + | Doch noch ist nicht alles Verloren, wir können uns der Lösung recht gut annähern. Bestimmte Integrale können wir mit numerischen Verfahren lösen, wodurch es zumindest möglich ist ein entsprechendes t anzunähern und mit entsprechenden Näherungsverfahren können wir uns auch verhältnismäßig schnell und gut annähern. | ||
| + | |||
| + | ===Numerische Integration=== | ||
| + | Da dieser Teil wohl etwas zu ausschweifend wäre möchte ich hier nur die Grundlegende Idee und eine sehr einfache Methode erwähnen. | ||
| + | |||
| + | Bei numerischen Verfahren wählt man üblicherweise ein paar Punkte der zu integrierenden Funktion aus und berechnet den Flächeninhalt des Kurvenstückes indem man häufig sehr grobe Annäherungen verwendet. Die wohl naivste Methode ist, wenn man sagt: | ||
| + | Integral[a bis b]( f(x) ) ~= | (b-a) * f( (b+a)/2 ) | | ||
| + | Also man berechnet sich den Flächeninhalt des Rechtecks, mit der Breite des entsprechenden Kurvenstückes und einem Punkt der Kurve (in diesem Fall der Punkt in der Mitte des Stückes). | ||
| + | |||
| + | Eine andere sehr bekannte Methode verwendet statt Rechtecken Trapeze und benötigt dafür natürlich bereits 2 Punkte der Kurve: | ||
| + | Integral[a bis b]( f(x) ) ~= | (b-a) * ( f(a) + f(b) )/2 | | ||
| + | |||
| + | Da eine solche Annäherung natürlich erfolgversprechender wird, desto kleiner der Abstand zwischen a und b ist, wird man üblicherweise einen größeren Bereich in mehrere (oder sogar sehr viele) kleinere Bereiche unterteilen: | ||
| + | Integral[a bis b]( f(x) ) = Integral[a bis k1]( f(x) ) + Integral[k1 bis k2]( f(x) ) + ... + Integral[kn bis b]( f(x) ) | ||
| + | Je kleiner die Teilbereiche werden, umso genauer wird das Ergebnis. | ||
| + | |||
| + | Generell kann man wohl sagen, dass bei komplexeren Integralen ein guter Mittelweg zu finden ist zwischen Genauigkeit und Rechenaufwand, sofwohl was die Anzahl der Teilstücke, als auch die Qualität der Berechnung der Teilstücke betrifft. | ||
| + | |||
| + | ===Näherungsverfahren=== | ||
| + | Auch hier gibt es mehrere Varianten, da es sich jedoch um eine monoton wachsende Funktion handelt, sind wohl alle Varianten brauchbar, wenn einige davon aber dennoch endlos um das Ziel herum oszillieren können. Wir besitzen nun eine Methode mit der wir beispielsweise das oben problematische Integral ganz gut annähern können. Wir können also jetzt bestimmten: | ||
| + | Im Zeitraum t0 bis t hat die Kurve eine Länge s. | ||
| + | Wir möchten aber nun für einen Länge s einen Zeitpunkt t (in Abhängigkeit von t0) finden. Dies erreichen wir, indem wir uns möglichst schnell an dieses t annähern. Ein Beispiel dafür ist das Newtonsche Näherungsverfahren. Wiederum soll jedoch nur ein grober Überblick über die Materie gegeben werden. | ||
| + | |||
| + | Wenn wir einen Zielwert (der Einfachheit halber immer f(x) = 0 ) besitzen, einen aktuellen Wert X1 und f(X1) = k, so wissen wir bei einer monoton steigenden Funktion bereits ob wir nach links oder nach rechts müssen. Ist k größer als 0 so müssen wir nach links. Ist k kleiner 0, so müssen wir nach rechts. Des weiteren können wir uns noch die Steigung der Funktion am Punkt X1 berechnen, wodurch wir auch eine recht gute Ahnung davon bekommen wie weit wir uns bewegen sollen. Dafür nehmen wir an, dass die Steigung annähernd gleich bleibt. Nun berechnen wir uns wie weit wir bei gleich bleibender Steigung gehen müssen und erhalten so unser X2. Diesen Vorgang wiederholen wir so lange bis wir einen genügend genauen Wert besitzen, oder der Wert längere Zeit nicht mehr genauer wird. Die Formel dafür lautet: | ||
| + | X(n+1) = Xn - f(Xn) / f'(Xn) | ||
| + | Und somit haben wir alle Werkzeuge zur Verfügung die wir benötigen, denn nun können wir den 0-Punkt der Funktion | ||
| + | Integral[t0 bis t]( f(x) ) - s = 0 | ||
| + | annähern, so dass wir ein t erhalten welches die gesuchte Weglänge gut annähert. Diese t können wir danach in unsere Formel ganz normal einsetzen und somit erhalten wir die Position und bei Bedarf natürlich auch wieder die Tangente oder einen Normalvektor. | ||
| + | |||
| + | ===Beispiel=== | ||
| + | Wir verwenden hier wieder eine Kurve im 2D-Raum welches wie unter "Polynome höheren Grades" aus 4 Punkten erstellt wurde. Ohne große Umschweife hier die beiden Formeln: | ||
| + | Ix = -31.5*t^3 + 58.5*t^2 - 28*t + 5 | ||
| + | Iy = 22.5*t^3 - 36*t^2 + 12.5*t + 3 | ||
| + | |||
| + | Wir implementieren diese direkt (also hardgecodet) um den Quellcode eher kurz und einfach zu halten (bisher C-Code): | ||
| + | /* x Wert der Kurve in Abhängigkeit der Zeit */ | ||
| + | double func_x( double t ) | ||
| + | { | ||
| + | return 5.0 - 28.0*t + 58.5*t*t - 31.5*t*t*t; | ||
| + | } | ||
| + | |||
| + | /* func_x'(t) also func_x abgeleitet. Ein Polynom lässt sich sehr einfach | ||
| + | * ableiten, der Einfachheit halber jedoch auch hier direkt angegeben. | ||
| + | */ | ||
| + | double func_dx( double t ) | ||
| + | { | ||
| + | return -28.0 + 117.0*t - 94.5*t*t; | ||
| + | } | ||
| + | |||
| + | /* y Wert der Kurve in Abhängigkeit der Zeit */ | ||
| + | double func_y( double t ) | ||
| + | { | ||
| + | return 3.0 + 12.5*t - 36.0*t*t + 22.5*t*t*t; | ||
| + | } | ||
| + | |||
| + | /* func_y'(t) also func_y abgeleitet */ | ||
| + | double func_dy( double t ) | ||
| + | { | ||
| + | return 12.5 - 72.0*t + 67.5*t*t; | ||
| + | } | ||
| + | |||
| + | /* Weg in Abhängigkeit der Zeit abgeleitet. */ | ||
| + | double func_ds( double t ) | ||
| + | { | ||
| + | return sqrt( func_dx(t)*func_dx(t) + func_dy(t)*func_dy(t) ); | ||
| + | } | ||
| + | |||
| + | Nun der erste etwas interessantere Teil, das numerische integrieren von func_ds: | ||
| + | /* Liefert eine Annäherung an das Integral von func mit den Schranken a und b. | ||
| + | * Parameter: | ||
| + | * a: untere Schranke | ||
| + | * b: obere Schranke | ||
| + | * sections: Anzahl der verwendeten Trapeze zur Annäherung, je höher desto genauer die Annäherung | ||
| + | * Wenn b kleiner als a ist, so wird ein negativer Wert zurück gegeben. | ||
| + | */ | ||
| + | double NIntegrate( double a, double b, int sections ) | ||
| + | { | ||
| + | int d; | ||
| + | double sum = 0.0; | ||
| + | double pos = a; | ||
| + | double pos2 = a + (b-a)/(double)sections; | ||
| + | double f = func_ds( pos ); | ||
| + | double f2; | ||
| + | |||
| + | for( d=0; d<sections; d++ ) | ||
| + | { | ||
| + | f2 = func_ds( pos2 ); | ||
| + | |||
| + | sum += fabs( (f+f2)*0.5*(b-a)/(double)sections ); | ||
| + | |||
| + | pos = pos2; | ||
| + | pos2 += (b-a)/(double)sections; | ||
| + | |||
| + | f = f2; | ||
| + | } | ||
| + | |||
| + | // Ist die untere Schranke a größer als die obere Schranke b, so negiere den Wert | ||
| + | if( a > b ) | ||
| + | return -sum; | ||
| + | else | ||
| + | return sum; | ||
| + | } | ||
| + | Mit dieser Funktion können wir uns nun bereits berechnen wie viel Weg zu einem Zeitpunkt t zurück gelegt wurde. Ein Beispiel hierfür folgt noch weiter unten. Um uns für einen gegebenen Weg s an einen Zeitpunkt t anzunähern an dem wir den Weg zurück gelegt haben, verwenden wir nun ein Näherungsverfahren. Wir wollen die Funktion | ||
| + | f(x) = Integral[0 bis t]( func_ds(x) ) - s | ||
| + | an 0 annähern. Für das Newton-Verfahren benötigen wir noch die Ableitung von f(x): | ||
| + | f'(x) = func_ds(x) | ||
| + | und nun können wir folgende Formel verwenden: | ||
| + | Xn+1 = Xn - (Integral[ 0 bis Xn ]( func_ds(x) ) - s) / func_ds(Xn) | ||
| + | Und genau das machen wir in folgender Funktion: | ||
| + | /* Nähert den Wert t für | ||
| + | * Integral[0 bis t]( func_ds(x) ) = Value | ||
| + | * an. | ||
| + | * Parameter: | ||
| + | * start: ein möglichst genau geschätzter Wert mit dem die Annäherung begonnen werden soll. | ||
| + | * Value: Zielwert nach obiger Formel. | ||
| + | * depth: Anzahl der Iterationen (bzw. um genau zu sein der Rekursionen) je höher dieser Wert desto genauer das Ergebnis | ||
| + | * sections: Wird an NIntegrate weitergereicht, je höher dieser Wert desto genauer das Ergebnis | ||
| + | */ | ||
| + | double FindValue( double start, double Value, int depth, int sections ) | ||
| + | { | ||
| + | double newval; | ||
| + | double f = func_ds( start ); | ||
| + | |||
| + | if( depth <= 0 ) | ||
| + | return start; | ||
| + | |||
| + | // verhindert Division durch 0. Extrem kleine Werte _könnten_ auch problematisch sein. | ||
| + | if( f < 0.0000001 && f > -0.0000001) | ||
| + | { | ||
| + | if( f >= 0.0f ) | ||
| + | newval = start - (NIntegrate( 0.0, start, sections ) - Value); | ||
| + | else | ||
| + | newval = start + (NIntegrate( 0.0, start, sections ) - Value); | ||
| + | } | ||
| + | else | ||
| + | { | ||
| + | // die Unterscheidung ob start > 0 ist wird bereits von NIntegrate durchgeführt | ||
| + | newval = start - (NIntegrate( 0.0, start, sections ) - Value) / f; | ||
| + | } | ||
| + | |||
| + | return FindValue( newval, Value, --depth, sections ); | ||
| + | } | ||
| + | Nun noch das ein oder andere Beispiel wie wir diese Funktionen verwenden: | ||
| + | /* Beispielshafte Verwendung der Funktionen */ | ||
| + | void main() | ||
| + | { | ||
| + | double FullKurveLength = NIntegrate( 0.0, 1.0, 100 ); | ||
| + | double TforS; | ||
| + | double KurveLength; | ||
| + | |||
| + | printf( "Die gesamte Kurvenlaenge (von Zeitpunkt 0 bis 1) betraegt ziemlich genau: %f\n", FullKurveLength ); | ||
| + | |||
| + | printf( "\n" ); | ||
| + | |||
| + | /* Parameter: | ||
| + | * a = 0.0: Wir möchten den zurückgelegten Weg angefangen von Zeitpunkt 0.0 | ||
| + | * b = 0.5: Wir möchten den zurückgelegten Weg bis zum Zeitpunkt 0.5, also von 0.0 bis 0.5 | ||
| + | * sections = 10: liefert wahrscheinlich ein eher ungenaues Ergebnis. | ||
| + | */ | ||
| + | KurveLength = NIntegrate( 0.0, 0.5, 10 ); | ||
| + | printf( "Ungeneau: in der haelfte der Zeit wurde %f Weg zurueck gelegt.\n", KurveLength ); | ||
| + | |||
| + | KurveLength = NIntegrate( 0.0, 0.5, 20 ); | ||
| + | printf( "Etwas geneauer: in der haelfte der Zeit wurde %f Weg zurueck gelegt.\n", KurveLength ); | ||
| + | |||
| + | KurveLength = NIntegrate( 0.0, 0.5, 100 ); | ||
| + | printf( "Recht geneau: in der haelfte der Zeit wurde %f Weg zurueck gelegt.\n", KurveLength ); | ||
| + | |||
| + | printf( "\n" ); | ||
| + | |||
| + | /* Parameter: | ||
| + | * start = 0.5: wir schätzen das der halbe Weg zum Zeitpunkt 0.5 zurück gelegt wurde | ||
| + | * Value = FullKurveLength * 0.5: wir möchten wissen zu welchem Zeitpunkt der halbe Weg zurück gelegt wurde | ||
| + | * depth & sections = 0: liefert wahrscheinlich ein eher ungenaues Ergebnis. | ||
| + | */ | ||
| + | TforS = FindValue( 0.5, FullKurveLength * 0.5, 5, 10 ); | ||
| + | printf( "Ungenau: zum Zeitpunkt %f wurde der halbe Weg zurueck gelegt.\n", TforS ); | ||
| + | |||
| + | TforS = FindValue( 0.5, FullKurveLength * 0.5, 10, 20 ); | ||
| + | printf( "Etwas genauer: zum Zeitpunkt %f wurde der halbe Weg zurueck gelegt.\n", TforS ); | ||
| + | |||
| + | TforS = FindValue( 0.5, FullKurveLength * 0.5, 50, 100 ); | ||
| + | printf( "Recht genau: zum Zeitpunkt %f wurde der halbe Weg zurueck gelegt.\n", TforS ); | ||
| + | }; | ||
| + | Als ausgabe dieses Tests erhalten wir: | ||
| + | Die gesamte Kurvenlaenge (von Zeitpunkt 0 bis 1) betraegt ziemlich genau: 9.201214 | ||
| + | |||
| + | Ungeneau: in der haelfte der Zeit wurde 5.582572 Weg zurueck gelegt. | ||
| + | Etwas geneauer: in der haelfte der Zeit wurde 5.558352 Weg zurueck gelegt. | ||
| + | Recht geneau: in der haelfte der Zeit wurde 5.550576 Weg zurueck gelegt. | ||
| + | |||
| + | Ungenau: zum Zeitpunkt 0.376217 wurde der halbe Weg zurueck gelegt. | ||
| + | Etwas genauer: zum Zeitpunkt 0.378924 wurde der halbe Weg zurueck gelegt. | ||
| + | Recht genau: zum Zeitpunkt 0.379795 wurde der halbe Weg zurueck gelegt. | ||
| + | Wir können uns nun auch die Zeitpunkte ausrechnen an denen 10%, 20%, ... des Weges zurück gelegt wurde und uns die Punkte auf der Kurve einzeichnen um auch einen visuelleren Vergleich zu erhalten: | ||
| + | |||
| + | [[Bild:KurvenlaengenInterpolation.gif]] | ||
| + | |||
| + | Rot: Die Punkte zu den Zeitpunkten 0.0, 0.1, 0.2, ..., 0.9, 1.0 | ||
| + | |||
| + | Blau: Die Punkte zu denen 0%, 10%, 20%, ..., 90%, 100% des Weges zurück gelegt wurde angenähert durch FindValue(...) mit depth = 5 und sections = 10 | ||
| + | |||
| + | Grün: Die Punkte zu denen 0%, 10%, 20%, ..., 90%, 100% des Weges zurück gelegt wurde angenähert durch FindValue(...) mit depth = 50 und sections = 100 | ||
| + | |||
| + | Gut zu erkennen ist auf diesem Bild auch, dass 10 Unterteilungen für einen das Integrieren von 0 bis 0.1 noch ganz gute Ergebnisse liefert, jedoch bei einem Wertebereich von 0 bis 1 schon ziemlich ungenau wird, somit macht es durchaus Sinn die Anzahl der Unterteilungen auch abhängig von der Größe des Bereiches zu machen. | ||
Aktuelle Version vom 17. Juni 2006, 18:15 Uhr
Bei Interpolationsverfahren geht es darum, aus wenigen Werten beliebig viele Werte zu generieren. Da die gegebenen Werte - wo Interpolation nötig ist - meistens als Stichproben gesehen werden können, werden verschiedenste Verfahren benötigt um auch die nicht gegebenen Werte den Ansprüchen entsprechend zu berechnen. Die Ansprüche variieren hierbei etwas anhand der Geschwindigkeitsanforderungen, des Zahlenraumes und nicht zuletzt anhand der Art und Weise wie man interpolieren möchte.
Inhaltsverzeichnis
Polynom Interpolationen
Wenn man N gegebene Werte hat, so kann man diese mit einem Polynom (N-1)ten Grades interpolieren. Eine Polynom Interpolationen besitzen die allgemeine Form:
I = (t^n)*Fn + (t^(n-1))*F(n-1) + ... + t*F1 + F0
Wobei:
t ... die Interpolationsposition im Wertebereich [0|1] Fx ... ein konstanter Wert oder Faktor (oder allgemein ein m-Dimensionaler Vektor) I ... das interpolierte Ergebnis, was ebenfalls ein einzelner Wert oder ein Vektor sein kann.
Durch die Vektor-Schreibweise sollte bereits klar sein, dass Polynom-Interpolationen für jede Dimension extrig berechnet werden, und somit auf beliebig viele Dimensionen erweiterbar sind.
Lineare Interpolation
Allgemein
Die einfachste Form einer Polynom-Interpolation ist die lineare Interpolation. Hierbei sind nur 2 Werte gegeben, somit kann man diese Werte mit einem Polynom ersten Grades interpolieren. Dieses ist (wie unschwer zu erraten) eine Gerade der Form:
I = t*F1 + F0
Diese (eher ungewöhnliche) Form der Geradengleichung entspricht der oben angegebenen Polynom-Interpolation in beliebiger Dimension. Die Berechnung der Faktoren Px erfolgt hier für jede Dimension getrennt. Gegeben seien 2 m dimensionale Punkte (A1, A2, ..., A(m-1), Am) und (B1, B2, ..., B(m-1), Bm). Nun lässt sich für jede Dimension d ein einfaches Gleichungssystem aufstellen:
Ad = 0*F1d + F0d Bd = 1*F1d + F0d
da wir mit einem Interpolationswert von 0 den ersten Punkt (A) erhalten wollen und einem Interpolationswert von 1 den zweiten Punkt (B) möchten. Dies umgeformt auf P1d und P0d ergibt:
F0d = Ad F1d = Bd - Ad
Diesen Rechenschritt wiederholen wir für jede Dimension.
Rechenbeispiel
Wir wollen 2 Punkte im 3 dimensionalen Raum interpolieren:
A: (2|5|0) B: (4|1|8)
Wir berechnen uns die Vektoren P1 und P0 wie oben angegeben, wobei x die erste und z die dritte Dimension dar stellen soll:
F0x = Ax = 2 F1x = Bx - Ax = 2 F0y = Ay = 5 F1y = By - Ay = -4 F0z = Az = 0 F1z = Bz - Az = 8
Somit erhalten wir die unsere Interpolationsgleichung:
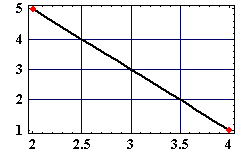
I(x|y|z) = t * (2|-4|8) + (2|5|0)
Das Ergebnis sieht nun folgendermaßen aus:
2 dimensionale Version des obigen Beispieles. Die gegebenen Punkte sind somit A(2|5) und B(4|1). Diese Punkte sind in rot dargestellt. Die Gerade beinhaltet alle Punkte für die gegebene Formel mit t im Wertebereich [0|1]
Polynome höheren Grades
Allgemein
Wie euch vielleicht schon bei der linearen Interpolation aufgefallen ist, ist eine Reihung der Punkte (vorher nur 2) erforderlich. Welcher PUnkt soll das Ergebnis mit t = 0 sein? Und welcher mit t=1? Wenn man mehr als 2 Punkte gegeben hat, so benötigt man zusätzlich noch die Informationen für welches t die beiden neuen Punkte gelten sollen. Meistens interpoliert man hier die Werte für t linear. Das heißt bei N gegebenen Punkten, soll der x-te Punkt für den t-Wert
t(Px) = x / (N-1) + 0
gegeben werden. Wobei:
t(Px) ... der t-Wert für den x-ten Punkt
Das (N-1) der Gleichung wird uns noch länger verfolgen, deshalb werden wir im weiteren Verlauf N-1 als n bezeichnen. Hier noch kurz die Anmerkung, dass man bei einem gegebenen Punkt natürlich keine Parameter benötigt sondern der Punkt immer gleich ist. Man kann sich dies (und alles darauffolgende) auch so vorstellen, dass wir den ersten gegebenen Punkt F0 als 0-Punkt annehmen und erst am "Ende" F0 addieren. Aus dieser Sichtweise heraus bekommen wir unser n = N-1.
Nun lässt sich wiederum das allgemeine (lineare) Gleichungssystem auffstellen:
P0 = t(P0)^n * Fn + t(P0)^(n-1) * F(n-1) + ... + t(P0) * F1 + F0 P1 = t(P1)^n * Fn + t(P1)^(n-1) * F(n-1) + ... + t(P1) * F1 + F0 ... Pn = t(Pn)^n * Fn + t(Pn)^(n-1) * F(n-1) + ... + t(Pn) * F1 + F0
Wobei:
Px ... der x-te Punkt t(Px) ... der t-Wert für den x-ten Punkt Fy ... der zu berechnende Faktor
Also ein Gleichungssystem mit n unbekannten und n (linear unabhängigen) Gleichungen, welches sich demnach eindeutig lösen lässt. Wobei dieses Gleichungssystem wiederum für jede Dimension extrig aufgestellt und berechnet werden muss! Da man (eindeutig lösbare) Gleichungssystem recht angenehm durch Matrizen-Mathematik lösen kann, empfiehlt sich auch folgende Schreibweise:
P = M * F
Wobei:
P ... ein N dimensionaler Vektor der die gegebenen Werte für den jeweiligen Punkt beinhaltet M ... eine NxN Matrix welche die t(Px)^y beinhaltet F ... ein N dimensionaler Vektor der die zu berechnenden Faktoren erhält und N ... wie gehabt die Anzahl der gegebenen Punkte und n = N - 1
Dies kann man nun umformen in:
M^-1 * P = F
Wobei:
M^-1 ... die inverse von M ist
Dadurch erhält man alle Werte Fy die man benötigt und kann somit für ein gegebenes t wiederum in die allgemeine Form:
I = (t^n)*Fn + (t^(n-1))*F(n-1) + ... + t*F1 + F0
einsetzen.
Rechenbeispiel
Wir wollen über 4 Punkte eine Polynominterpolation im 2 dimensionalen Raum. Diese sind:
P0: (5|3) P1: (1|4) P2: (4|2) P3: (1|2)
Wir legen nun zuerst wieder die t-Werte für die Punkte fest, und sagen:
P0 bei t=0 P1 bei t=1/3 P2 bei t=2/3 P3 bei t=1
Und berechnen uns nun die Matrix M mit diesen t-Werten:
| 0^3 0^2 0^1 1 |
M = | 0.33^3 0.33^2 0.33 1 |
| 0.66^3 0.66^2 0.66 1 |
| 1^3 1^2 1^1 1 |
Und berechnen uns nun die inverse M^-1:
| -4.5 13.5 -13.5 4.5 |
M^-1 = | 9 -22.5 18 -4.5 |
| -5.5 9 -4.5 1 |
| 1 0 0 0 |
Nun nehmen wir den P-Vektor der ersten Dimension:
Px = (5|1|4|1)
und multiplizieren ihn mit der Matrix wodurch wir
Fx = M^-1 * Px = (-58.5|90|35.5|5)
erhalten. Nun das selbe für die zweite Dimension:
Py = (3|4|2|2)
und wiederum
Fy = M^-1 * Py = (22.5|-36|12.5|3)
Somit ist unsere endgültige Formel für die Interpolation:
Ix = -58.5 * t^3 + 90 * t^2 - 35.5 * t + 5 Iy = 22.5 * t^3 - 36 * t^2 + 12.5 * t + 3
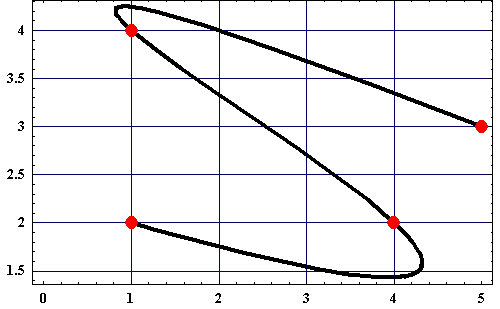
Das Ergebnis sieht nun folgendermaßen aus:
Oben angegebenes Beispiel grafisch dargestellt. Die Punkte P0 bis P3 sind rot dargestellt. Die Kurve beinhaltet alle Punkte der gegebenen Funktionen für ( Ix , Iy ) mit t im Wertebereich [0|1].
Kurven mit gegebenen Tangenten
Wir haben die oben gegebene Polynom-Gleichung für N Punkte. Wenn wir nun zusätzlich J Tangenten angeben möchten, so haben wir natürlich J zusätzliche Gleichungen und benötigen ein Polynom (N+K-1)ten Grades. Als erstes stellen wir wiederum eine derartige Polynom-Gleichung auf, jedoch mit dem Unterschied das wir dies gleich mit dem (N+J-1)ten Grad machen. Des weiteren müssen wir für jede Tangente Festlegen bei welchem t^x wir sie einbrigen möchten. Der Einfachheit halber wird hier die Reihung: zuerst die Punkte (also einem t^x mit höherem x) und danach die Tangenten (also einem t^x mit niedrigerem x als die Punkte bis hin zu x=0) verwendet. Daraus ergibt sich die allgemeine Form für die Punkte:
P0 = t(P0)^(n+J) * F(n+J) + t(P0)^(n+J-1) * F(n+J) + ... + t(P0)^(J+1) * F(J+1) + t(P0)^J * F(J) + t(P0)^(J-1) * F(J-1) + t(P0)^(J-2) * F(J-2) + ... + t(P0) * F1 + F0 P1 = t(P1)^(n+J) * F(n+J) + t(P1)^(n+J-1) * F(n+J) + ... + t(P1)^(J+1) * F(J+1) + t(P1)^J * F(J) + t(P1)^(J-1) * F(J-1) + t(P1)^(J-2) * F(J-2) + ... + t(P1) * F1 + F0 ... Pn = t(Pn)^(n+J) * F(n+J) + t(Pn)^(n+J-1) * F(n+J) + ... + t(Pn)^(J+1) * F(J+1) + t(Pn)^J * F(J) + t(Pn)^(J-1) * F(J-1) + t(Pn)^(J-2) * F(J-2) + ... + t(Pn) * F1 + F0
Wobei:
Px ... der x-te Punkt t(Px) ... der t-Wert für den x-ten Punkt F(n+J) bis F(J) ... der zu berechnende Faktor für den (N-1)ten Punkt F(J-1) bis F(0) ... der zu berechnende Faktor für die J-te Tangente
Nun benötigen wir natürlich noch weitere Gleichungen für die Tangenten um das Gleichungssystem eindeutig lösbar zu machen. Eine Tangente K (hier wird bewusst K und nicht T gewählt) für den Xten Punkt lässt sich durch eine Ableitung nach t berechnen:
K(Px) = (n+J) * t(Px)^(n+J-1) * F(n+J) + (n+J-1) * t(Px)^(n+J-2) * F(n+J-1) + ... + (J+1) * t(Px)^(J) * F(J+1) + J * t(Px)^(J-1) * F(J) + (J-1) * t(Px)^(J-2) * F(J-1) + (J-2) * t(Px)^(J-3) * F(J-2) + ... + t(Px) * F2 + F1 + ( 0 * F0 )
Mit diesen Gleichungssystemen können wir wiederum eine Matrix formen, diese invertieren und los legen. Aber (meines Erachtens) erklärt sich dies am besten an einem Beispiel.
Hermite Kurven
Hermite Kurven sind Interpolationsfunktionen wo der Anfangs- und Endpunkt eine bestimmte Tangente aufweist. Üblicherweise werden Hermite Kurven zusätzlich noch auf 2 gegebene Punkte beschränkt, was wir hier der Einfachheit halber beibehalten wollen. Wir haben 2 Punkte, 2 Tangenten wodurch wir auf ein Polynom (N+J-1) = (2+2-1) = 3ten Grades kommen. Alse stellen wir eine Polynomgleichung für 2 gegebene Punkte auf, wobei der erste Punkt den Zeitpunkt 0 und der zweite Punkt den Zeitpunkt 1 erhält. Dadurch kommen wir auf zwei triviale Gleichungen:
P0 = 0 * F(3) + 0 * F(2) + 0 * F(1) + 1 * F(0) P1 = 1 * F(3) + 1 * F(2) + 1 * F(1) + 1 * F(0)
Nun noch die Tangentengleichungen die sich aus der oben angegebenen K(Px) - Formel ergeben:
K0 = 0 * F(3) + 0 * F(2) + 1 * F(1) + 0 * F(0) K1 = 3 * F(3) + 2 * F(2) + 1 * F(1) + 0 * F(0)
Dies ist unser lineares Gleichungssystem woraus wir wiederum unsere Matrix gewinnen:
| 0 0 0 1 |
M = | 1 1 1 1 |
| 0 0 1 0 |
| 3 2 1 0 |
Und natürlich die Formel:
W = M * F
Wobei:
W ... ein Vektor ist der die Werte P0, P1, K0, K1 (in dieser Reihenfolge) beinhaltet M ... die oben gegebene Matrix F ... der Vektor der die zu berechnenden Werte beinhaltet.
Diese Matrix invertiert ergibt:
| 2 -2 1 1 |
M^-1 = | -3 3 -2 -1 |
| 0 0 1 0 |
| 1 0 0 0 |
Somit können wir den F-Vektor berechnen durch
M^-1 * W = F
Wenn wir nun also für W die Werte (2,3,-1,1) hätten, wobei hier
2 ... der erste Punkt 3 ... der zweite Punkt -1 ... die Tangente für den ersten Punkt 1 ... die Tangente für den zweiten Punkt
so ergeben sich daraus die Faktoren:
F = M^-1 * W = (-2,4,-1,2)
Wodruch wir für unsere Kurve folgende Formel erhalten:
f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2
Da die Dimensionen hier ebenfalls unabhängig sind, können Hermit-Kurven auf beliebig viele Dimensionen erweitert werden.
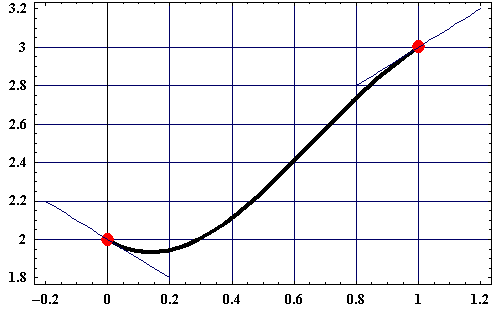
Das Ergebnis sieht nun folgendermaßen aus:
Oben angegebenes Beispiel grafisch dargestellt. Die beiden Punkte sind rot dargestellt, die beiden Tangenten sind als blaue Geraden eingezeichnet. Die Kurve beinhaltet alle Punkte der gegebenen Funktionen für t im Wertebereich [0|1].
Tangenten von Kurven
Besitzt man die Funktion für eine Kurve so lässt sich die Tangente durch das differenzieren dieser Funktion ermitteln. Aus unserem vorigen Beispiel wäre dies:
f(t) = t^3 * (-2) + t^2 * 4 + t * (-1) + 2 f'(t) = -6 * t^2 + 8 * t - t
Da die Dimensionen einer derartigen Kurve wie gesagt unabhängig voneinander behandelt werden können, kann man dadurch die Tangente in der entsprechenden Dimension erhalten.
Interpolation mit anderen Funktionen
Bisher wurden nur Interpolationen gezeigt, bei denen der t-Wert potenziert wurde. Es wurde immer ein Anfangspunkt verwendet, für den der t-Wert 0 sein sollte, und ein Endpunkt für den der t-Wert 1 sein sollte. Wir können natürlich jede beliebige Funktion für die Interpolation verwenden wo dies zutrifft. Wenn wir möchten können wir natürlich auch eine Funktion verwenden wo der Anfangspunkt bei t=X und der Endpunkt bei t=Y zu finden ist, denn eine derartige Funktion können wir wiederum umformen zu einer Funktion für die wir einen Anfangspunkt mit t=0 und einen Endpunkt mit t=1 haben.
Andere Funktionen werden meistens (nicht immer) bei nur 2 gegebenen Punkten verwendet. Hier wird meistens aus einem t-Wert im Bereich [0|1] ein neuer Wert u im Bereich [1|0] berechnet, welcher danach ähnlich wie bei der linearen Interpolation verwendet wird. Also:
u = f(t) Interpolierter_Wert = I(t) = u * Startwert + (1-u) * Endwert
Wobei:
f(t) ... die Interpolationsfunktion, welche bei t=0 1 zurück liefert und bei t=1 0 ist. Interpolierter_Wert ... das Ergebnis.
Mögliche andere Funktionen sind nun beispielsweise:
Cosinus ähnliche Interpolation
Cosinus Interpolation
Der Cosinus liefert Werte zwischen -1 und 1. Wir wollen einen eindeutigen y-Wert für y=Cos(t), somit verwenden wir nur t-Werte im Wertebereich von 0 bis 180 Grad (bzw. 0 bis Pi Radianten), denn bei t=181 Grad würden wir ja den selben Wert erhalten wie für t=179 Grad.
Der t-Wert wird für den Cosinus im Wertebereich [0|Pi] bzw. [0|180Grad] benötigt. Um nun einen t-Wert (wie zuvor) im Wertebereicheich von [0|1] verwenden zu können, multiplizieren wir ihn einfach mit Pi. Also verwenden wir einfach
t2 = t * Pi
bzw. das Ganze mit Grad:
t2 = t * 180
Der Ausgabewert von Cosinus ist im Wertebereich [1|-1]. Um ihn auf den Wertebereich [1|0] zu bringen, müssen wir ihn transformieren. Dafür formen wir um:
f(t2) = Cos(t2) g(t2) = f(t2)/2 + 1/2 = ( 1 + f(t2) ) / 2 = ( 1 + Cos(t2) ) / 2
Und nun noch t2 durch t ersetzt:
g(t) = ( 1 + Cos(t*Pi) ) / 2
bzw. das Ganze mit Grad:
g(t) = ( 1 + Cos(t*180) ) / 2
Wir haben nun eine Formel die uns bei t=0 einen Wert von 1 liefert und bei t=1 einen Wert von 0. Dies können wir in unsere allgemeine Funktion einsetzen:
Interpolierter_Wert = I(t) = g(t) * Startwert + ( 1 - g(t) ) * Endwert
Und für g(t) eingesetzt:
Interpolierter_Wert = I(t) = ( (1+Cos(t*Pi))/2 ) * Startwert + ( 1 - (1+Cos(t*Pi))/2 ) * Endwert
bzw. das Ganze mit Grad:
Interpolierter_Wert = I(t) = ( (1+Cos(t*180))/2 ) * Startwert + ( 1 - (1+Cos(t*180))/2 ) * Endwert
Nun die Frage warum der ganze Aufwand, also warum nicht linear interpolieren? Um dies zu beantworten müssen wir die Steigungen dieser Funktion betrachten, wofür wir die Ableitung der Funktion berechnen:
I'(t) = 1/2 * Endwert * Pi * Sin( t * Pi ) - 1/2 * Startwert * Pi * Sin( t * Pi )
Sieht kompliziert aus, aber wenn wir nun t=0 annehmen so erhalten wir für Sin( t * Pi ) ebenfalls 0. Wenn wir für t=1 annehmen so erhalten wir für Sin( t * Pi ) wiederum 0. Und dadurch erhalten wir an beiden Enden eine Steigung von 0.
Was können wir machen mit einer Funktion die an beiden Enden eine Steigung von 0 aufweist? Ganz einfach: wir können mehrere dieser Funktionen aneinander reihen, ohne das man einen übergang erkennt. Somit können wir sagen:
Bei t im Bereich [0|1] verwende als Startwert 3 und als Endwert 1 Bei t im Bereich ]1|2] verwende als Startwert 1 und als Endwert 7 Bei t im Bereich ]2|3] verwende als Startwert 7 und als Endwert 8
Und wenn wir alle 3 Funktionen mit dem Wertebereich [0|1] verwenden (oder mathematisch ausgedrückt: I2(t) = I(t modulo 1) ), so erhalten wir eine Kurve ohne Kanten, oder um es etwas mathematischer auszudrücken: diese Funktion ist im Wertebereich ]0|3[ ableitbar, also in diesem Wertebereich auch stetig.
Und um die Ästhetik hinter diesen Formeln zu zeigen, ein Vergleich von linearer- zu cosinus-Interpolation:
Quadratische Annäherung der Cosinus Interpolation
Da die Berechnung des Cosinus eine etwas aufwändigere Angelegenheit ist, wünscht man sich hin und wieder eine Funktion die ähnlich aussieht und die gleichen Bedingungen (also eine Steigung von 0 an Start- und Endpunkt) erfüllt. Hierfür kann man 2 quadratische Funktionen verwenden die folgendes erfüllen müssen:
- Beide Kurven müssen einen gemeinsamen Punkt besitzen, also I1(t) = I2(t) für t im Wertebereich [0|1]
- An diesem Punkt müssen beide Kurven die selbe Steigung besitzen, also es existiert ein ( I1(X) = I2(X) wo auch gilt I1'(X) = I2'(X) ).
- Steigung (also Ableitung) bei t=0 und t=1 soll 0 sein
- Die Kurve sollte symmetrisch sein bezogen auf t=0.5, so das gilt: I1(t) = 1-I2(1-t). Somit muss gleichzeitig der Punkt wo gilt I1(t) = I2(t) bei 0.5 liegen.
Wir können uns nun aus der ersten und dritten Bedinung einfach die beiden Formeln herleiten, aber um es kurz zu machen:
Wenn t <= 0.5 dann I1(t) = -2*t^2 + 1 Wenn t > 0.5 dann I2(t) = 2*t^2 - 4*t + 2 = 2 * (1-t)^2
Nun zeigen wir, dass die oben angegebenen Bedingungen erfüllt sind:
- I1(0.5) = -2*0.5^2 + 1 = 0.5; I2(0.5) = 2 * (1-0.5)^2) = 0.5
- I1'(t) = -4t, I1'(0.5) = -2; I2'(t) = 4*t - 4, I2'(0.5) = -2
- I1'(0) = -4*0 = 0; I2'(1) = 4*1 - 4) = 0
- I1(t) = 1-I2(1-t) => -2*t^2 + 1 = 1 - (2*(1-t)^2 - 4*(1-t) + 2) => -2*t^2 + 1 = 1 - (2 - 4*t + 2*t^2 - 4 + 4*t + 2) => -2*t^2 + 1 = -2*t^2 + 1
Cosinus ähnliche Interpolation durch Polynominterpolation
Wenn wir eine Polynominterpolation mit den beiden Endtangenten 0 berechnen wollen, so verwenden wir eine Hermite Kurve. Hierbei verwenden wir die Werte:
1 ... Startpunkt 0 ... Endpunkt 0 ... Steigung bei Startpunkt 0 ... Steigung bei Endpunkt
Mit der unter Hermit Kurven angegebenen Matrix M^-1 können wir uns nun die dazugehörige Funktion berechnen und erhalten:
I(t) = 2*t^3 - 3*t^2 + 1
Die ersten beiden Bedingungen von vorher sind automatisch erfüllt, da es sich nur um eine Funktion handelt. Für die 3. und 4. Bedingung lässt sich ebenfalls verhältnismäßig einfach zeigen das sie erfüllt sind.
Vergleich der Cosinus ähnlichen Interpolationsarten
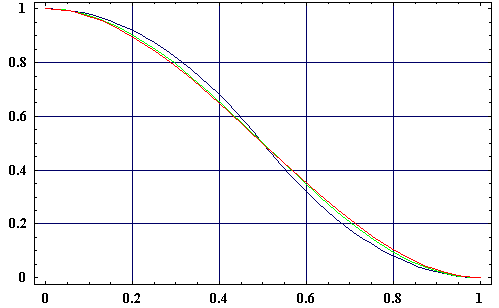
Und zu guter letzt hier noch die grafische Veranschaulichung der etwas zahlenbeladenen Funktionen.
Die 3 Cosinus ähnlichen Funktionen graphisch dargestellt:
- Grün: Cos-Interpolation
- Rot: Polynom-Interpolation
- Blau: Quadratische Annäherung
Interpolierte Flächen
Bisher wurden ausschließlich Kurven betrachtet. Aus Kurven lassen sich jedoch ohne größere Umstände auch Flächen bilden. Hier hat man zwei (unterschiedliche) t-Werte und eine Matrix von Punkten gegeben, wobei jeder Punkt gegebenenfalls noch 1 oder 2 Tangenten besitzen kann. Um einen Punkt einer Fläche zu berechnen interpoliert man zuerst die Punkte für jede Zeile der Punktmatrix. Nachdem man nun die interpolierten Punkte für jede Zeile besitzt kann man sich mit diesen Punkten ein neues Gleichungssystem aufstellen und wiederum eine Kurve bilden. Diese Kurve interpoliert man wiederum mit dem zweiten gegebenen t-Wert. Dies lässt sich auf beliebig viele Dimensionen nach dem gleichen Schema erweitern, üblicherweise wird dies jedoch nur für Oberflächen (also 2D) benötigt.
Normalvektoren
Besitzt man Flächen und berechnet sie nach dem gegebenen Schema, so berechnet man sich zuerst auch mehrere Kurven von denen man die Tangenten berechnen kann. Interpoliert man nun diese Tangenten mit der gleichen Kurvenfunktion wie die resultierenden Punkte, und berechnet sich aus der resultierenden Kurvenfunktion ebenfalls die Tangente, so erhält man 2 Tangenten. Aus diesen beiden Tangenten kann nun mit einem Kreuzprodukt ein Normalvektor errechnet werden.
Kurvenlängen-Interpolation
Es könnte erwünscht sein (beispielsweise für Kamerafahrten, Keyframe Interpolationen jeglicher Art oder auch bei der Interpolation von Positionsangaben die man beispielsweise über ein Netzwerk erhält), dass man über keine fixe Achse t interpolieren möchte, sondern über die Kurvenlänge.
Bei den typischen physikalischen Beispielen besitzt man meist eine Geschwindigkeit welche durch Beschleunigung verändert wird. Also wenn man einen Ball senkrecht hoch wirft, so gibt es einen Punkt an dem er komplett stehen bleibt. Für diese Art von physikalischen Berechnungen wird man also kaum eine Kurvenlängen-Interpolation benötigen.
Wenn man jedoch sehr langsame Geschwindigkeiten besitzt, also beispielsweise zu fuß geht, so haben wir eine nahezu konstante Gehgeschwindigkeit, egal ob wir eine Kurve gehen oder nicht. Wenn wir noch weiter gehen und auf einer Straße oder einer Rennstrecke alle 100 Meter ein Längenangabenschild hin stellen möchten, so ist uns Beschleunigung und auch die Geschwindigkeit vollkommen egal. Wir hätten also am liebsten eine Funktion P(s), welche uns den Punkt der Kurve für für Kilometer (oder Meter) s liefert.
Der eindimensionale Fall
Dieser Teil soll lediglich als Erklärung dienen, besitzt in der Praxis aber kaum Relevanz.
Im Eindimensionalen Fall kann man sich dies noch sehr gut veranschaulichen. Wenn ich eine gerade Strecke besitze und meine 1D-Koordinaten kenne, so kann ich ganz einfach sagen: zum Zeitpunkt t bin ich Betrag( f(t) - f(t0) ) Meter (allg. Einheiten) gegangen. Interessant wir es noch mal wenn ich die Richtung ändere, also wenn ich bei Kilometer 4 merke das ich etwas zu Hause vergessen habe, noch einmal umdrehe und dann weiter fahre. In diesem Fall kann ich nicht sagen: ich befinde mich an Position 10 Kilometer entfernt => ich bin 10 Kilometer gegangen, sondern in Wirklichkeit habe ich noch zusätzlich 8 Kilometer umweg hinter mir.
Dieses simple beispiel mathematisch ausgedrückt:
wenn f(t) monoton steigend oder monoton fallend ist: Kurvenlänge(t) = | f(t) - f(t0) | Sonnst: Kurvenlänge = Integral[t0 bis t]( f'(t) )
Beim Integrieren müssen wir nun aufpassen, ob unsere Stammfunktion 0-Stellen besitzt. Bei jeder solchen 0-Stelle Zx zerteilen wir die Wertebereiche:
W = [t0, Z1, Z2, Z3, ..., Zn, t]
Kurvenlänge(t) = Summe[ n=1 bis Elemente von W ]( Integral[W[n-1] bis W[n]]( f'(t) )
Da wir nun in der Stammfunktion alle 0-Stellen berücksichtigt haben können wir das Integral "kürzen", also
Kurvenlänge(t) = Summe[ n=1 bis Elemente von W ]( | f(w[n]) - f(w[n-1]) | )
Das Integral macht hier also nichts anderes als Richtungswechsel zu erkennen, denn bei einem Richtungswechsel in 1D ändert sich das Vorzeichen der Ableitung einer Funktion, und für jeden Vorzeichenwechsel muss es auch einen 0-Punkt geben wenn es sich um eine stetige Funktion handelt.
Wir kennen nun also den Weg den wir zu einem bestimmten Zeitpunkt zurückgelegt haben. Wir wollen jedoch den Zeitpunkt wissen an dem wir eine bestimmte Weglänge zurückgelegt haben, um die Funktion f(t) durch f(t(s)) = g(s) wodurch g(s) eine Funktion ist wo wir die Position für einen bestimmte Kurvenlänge erhalten.
Wir müssen also ein t finden für das gilt
Kurvenlänge(t) = s
und können danach dieses t in unsere Ursprüngliche Kurvengleichung einsetzen.
Und nun mit voller Wucht: warum bringt uns das alles ganz und gar nichts? Wenn wir eine Eindimensionale "Kurve" besitzen und wir wollen diese über die Kurvenlänge parametrisieren, so sagen wir schlicht und ergreifend:
x = x0 +/- s
wenn wir nicht mehrere Fälle besitzen. Wenn wir Fallunterscheidungen bekommen, so gibt es (wie im mehrdimensionalen Fall noch verdeutlicht wird) natürlich auch Methoden mit denen wir diese Fallunterscheidungen umgehen können (namentlich: numerische Integration). Dennoch ist die Funktion wohl in nahezu allen Fällen einfacher mit derartigen Fallunterscheidungen zu berechnen.
Beispiel
Ein Beispiel noch am Rande, wie man unschwer erahnen kann, gibt es eher wenig alltäglichere Beispiele die nicht zu trivial und von Interesse wären:
Wir besitzen eine gedämpfte Schwingung mit der Formel
f(t) = e^(-t) * sin(t)
und möchten aus unerfindlichen Gründen wissen wo sich der schwingende Körper befindet wenn er den Weg s zurückgelegt hat.
Wir berechnen uns die Ableitung
f'(t) = e^(-t) * cos(t) - e^(-t) * sin(t)
und nun die 0-Stellen, also
f'(t) = 0
davon gibt es aber natürlich jede Menge ... aber wir begnügen und mit den ersten 3:
f'(PI/4) = 0 | f(PI/4) ~= 0.322 f'(~3.927) = 0 | f(3.927) ~= -0.014 f'(~7.069) = 0 | f(7.069) ~= 0.0006
Da der Startpunkt (t=0) natürlich auch bei 0 liegt, erhalten wir also jetzt für unsere Position in Abhängigkeit der Weglänge s:
g(s) = s für s im Bereich [0,0.322] g(s) = 2*0.322-s für s im Bereich ]0.322|0.658] wobei 0.658 = 0.322 + | 0.322-0.014 | g(s) = s-2*0.322-2*0.014 für s im Bereich ]0.658|0.6585] wobei 0.6586 = 0.322 + | 0.322 - (-0.014) | + | -0.014 - 0.0006 |
Kurven in höheren Dimensionen
Im allgemeinen Fall kann eine Kurve in einer bestimmten Dimension als Vektor von Funktionen dargestellt werden:
| x(t) |
P(t) = | y(t) |
| z(t) |
| ... |
wir können die Tangente berechnen indem wir in jeder Dimensionen die Funktion ableiten:
| x'(t) |
T(t) = | y'(t) |
| z'(t) |
| ... |
und natürlich handelt es sich nun nicht um irgendeine Tangente, sondern um die Tangente welche auch die Änderungsgeschwindigkeit der Kurve abhängig von t beschreibt. Wir können die Länge dieser Tangente also als Geschwindigkeit der Kurve betrachten. Die Länge eines Vektors ist ein skalarer Wert, also erhalten wir für die Geschwindigkeit zu einem Zeitpunkt t die Funktion:
Geschwindigkeit(t) = | T(t) |
Der Betrag der Tangente wir nun folgendermaßen gebildet:
Geschwindigkeit(t) = Wurzel( x'(t)^2 + y'(t)^2 + z'(t)^2 + ... )
Nun besitzen wir eine Funktion für die Geschwindigkeit der Kurve welche uns integriert die Länge der Kurve bis zum Zeitpunkt t angibt. Im Gegensatz zum eindimensionalen Fall (wo dies eher wenig Sinn hatte) quadrieren wir hier jeden verwendeten Wert, wodurch diese Funktion niemals < 0 werden kann, somit müssen wir beim integrieren auch nicht auf 0-Stellen aufpassen.
Wir Integrieren nun:
Kurvenlänge(t) = Integral[t0 bis t]( Geschwindigkeit(t) )
Und hier stoßen wir an einen unangenehmen Punkt. Nehmen wir ein "einfaches" Polynom für x(t), y(t) und z(t). An einem Integral wie aus unserem Polynom-Beispiel:
Integral[t0 bis t]( Wurzel( (-58.5*t^3 + 90*t^2 - 35.5*t + 5)^2 + (22.5*t^3 - 36*t^2 + 12.5*t + 3)^2 ) )
scheitern sogar gute Mathematik-Bibliotheken, und von normalsterblichen Menschen ganz zu schweigen.
Doch noch ist nicht alles Verloren, wir können uns der Lösung recht gut annähern. Bestimmte Integrale können wir mit numerischen Verfahren lösen, wodurch es zumindest möglich ist ein entsprechendes t anzunähern und mit entsprechenden Näherungsverfahren können wir uns auch verhältnismäßig schnell und gut annähern.
Numerische Integration
Da dieser Teil wohl etwas zu ausschweifend wäre möchte ich hier nur die Grundlegende Idee und eine sehr einfache Methode erwähnen.
Bei numerischen Verfahren wählt man üblicherweise ein paar Punkte der zu integrierenden Funktion aus und berechnet den Flächeninhalt des Kurvenstückes indem man häufig sehr grobe Annäherungen verwendet. Die wohl naivste Methode ist, wenn man sagt:
Integral[a bis b]( f(x) ) ~= | (b-a) * f( (b+a)/2 ) |
Also man berechnet sich den Flächeninhalt des Rechtecks, mit der Breite des entsprechenden Kurvenstückes und einem Punkt der Kurve (in diesem Fall der Punkt in der Mitte des Stückes).
Eine andere sehr bekannte Methode verwendet statt Rechtecken Trapeze und benötigt dafür natürlich bereits 2 Punkte der Kurve:
Integral[a bis b]( f(x) ) ~= | (b-a) * ( f(a) + f(b) )/2 |
Da eine solche Annäherung natürlich erfolgversprechender wird, desto kleiner der Abstand zwischen a und b ist, wird man üblicherweise einen größeren Bereich in mehrere (oder sogar sehr viele) kleinere Bereiche unterteilen:
Integral[a bis b]( f(x) ) = Integral[a bis k1]( f(x) ) + Integral[k1 bis k2]( f(x) ) + ... + Integral[kn bis b]( f(x) )
Je kleiner die Teilbereiche werden, umso genauer wird das Ergebnis.
Generell kann man wohl sagen, dass bei komplexeren Integralen ein guter Mittelweg zu finden ist zwischen Genauigkeit und Rechenaufwand, sofwohl was die Anzahl der Teilstücke, als auch die Qualität der Berechnung der Teilstücke betrifft.
Näherungsverfahren
Auch hier gibt es mehrere Varianten, da es sich jedoch um eine monoton wachsende Funktion handelt, sind wohl alle Varianten brauchbar, wenn einige davon aber dennoch endlos um das Ziel herum oszillieren können. Wir besitzen nun eine Methode mit der wir beispielsweise das oben problematische Integral ganz gut annähern können. Wir können also jetzt bestimmten:
Im Zeitraum t0 bis t hat die Kurve eine Länge s.
Wir möchten aber nun für einen Länge s einen Zeitpunkt t (in Abhängigkeit von t0) finden. Dies erreichen wir, indem wir uns möglichst schnell an dieses t annähern. Ein Beispiel dafür ist das Newtonsche Näherungsverfahren. Wiederum soll jedoch nur ein grober Überblick über die Materie gegeben werden.
Wenn wir einen Zielwert (der Einfachheit halber immer f(x) = 0 ) besitzen, einen aktuellen Wert X1 und f(X1) = k, so wissen wir bei einer monoton steigenden Funktion bereits ob wir nach links oder nach rechts müssen. Ist k größer als 0 so müssen wir nach links. Ist k kleiner 0, so müssen wir nach rechts. Des weiteren können wir uns noch die Steigung der Funktion am Punkt X1 berechnen, wodurch wir auch eine recht gute Ahnung davon bekommen wie weit wir uns bewegen sollen. Dafür nehmen wir an, dass die Steigung annähernd gleich bleibt. Nun berechnen wir uns wie weit wir bei gleich bleibender Steigung gehen müssen und erhalten so unser X2. Diesen Vorgang wiederholen wir so lange bis wir einen genügend genauen Wert besitzen, oder der Wert längere Zeit nicht mehr genauer wird. Die Formel dafür lautet:
X(n+1) = Xn - f(Xn) / f'(Xn)
Und somit haben wir alle Werkzeuge zur Verfügung die wir benötigen, denn nun können wir den 0-Punkt der Funktion
Integral[t0 bis t]( f(x) ) - s = 0
annähern, so dass wir ein t erhalten welches die gesuchte Weglänge gut annähert. Diese t können wir danach in unsere Formel ganz normal einsetzen und somit erhalten wir die Position und bei Bedarf natürlich auch wieder die Tangente oder einen Normalvektor.
Beispiel
Wir verwenden hier wieder eine Kurve im 2D-Raum welches wie unter "Polynome höheren Grades" aus 4 Punkten erstellt wurde. Ohne große Umschweife hier die beiden Formeln:
Ix = -31.5*t^3 + 58.5*t^2 - 28*t + 5 Iy = 22.5*t^3 - 36*t^2 + 12.5*t + 3
Wir implementieren diese direkt (also hardgecodet) um den Quellcode eher kurz und einfach zu halten (bisher C-Code):
/* x Wert der Kurve in Abhängigkeit der Zeit */
double func_x( double t )
{
return 5.0 - 28.0*t + 58.5*t*t - 31.5*t*t*t;
}
/* func_x'(t) also func_x abgeleitet. Ein Polynom lässt sich sehr einfach
* ableiten, der Einfachheit halber jedoch auch hier direkt angegeben.
*/
double func_dx( double t )
{
return -28.0 + 117.0*t - 94.5*t*t;
}
/* y Wert der Kurve in Abhängigkeit der Zeit */
double func_y( double t )
{
return 3.0 + 12.5*t - 36.0*t*t + 22.5*t*t*t;
}
/* func_y'(t) also func_y abgeleitet */
double func_dy( double t )
{
return 12.5 - 72.0*t + 67.5*t*t;
}
/* Weg in Abhängigkeit der Zeit abgeleitet. */
double func_ds( double t )
{
return sqrt( func_dx(t)*func_dx(t) + func_dy(t)*func_dy(t) );
}
Nun der erste etwas interessantere Teil, das numerische integrieren von func_ds:
/* Liefert eine Annäherung an das Integral von func mit den Schranken a und b.
* Parameter:
* a: untere Schranke
* b: obere Schranke
* sections: Anzahl der verwendeten Trapeze zur Annäherung, je höher desto genauer die Annäherung
* Wenn b kleiner als a ist, so wird ein negativer Wert zurück gegeben.
*/
double NIntegrate( double a, double b, int sections )
{
int d;
double sum = 0.0;
double pos = a;
double pos2 = a + (b-a)/(double)sections;
double f = func_ds( pos );
double f2;
for( d=0; d<sections; d++ )
{
f2 = func_ds( pos2 );
sum += fabs( (f+f2)*0.5*(b-a)/(double)sections );
pos = pos2;
pos2 += (b-a)/(double)sections;
f = f2;
}
// Ist die untere Schranke a größer als die obere Schranke b, so negiere den Wert
if( a > b )
return -sum;
else
return sum;
}
Mit dieser Funktion können wir uns nun bereits berechnen wie viel Weg zu einem Zeitpunkt t zurück gelegt wurde. Ein Beispiel hierfür folgt noch weiter unten. Um uns für einen gegebenen Weg s an einen Zeitpunkt t anzunähern an dem wir den Weg zurück gelegt haben, verwenden wir nun ein Näherungsverfahren. Wir wollen die Funktion
f(x) = Integral[0 bis t]( func_ds(x) ) - s
an 0 annähern. Für das Newton-Verfahren benötigen wir noch die Ableitung von f(x):
f'(x) = func_ds(x)
und nun können wir folgende Formel verwenden:
Xn+1 = Xn - (Integral[ 0 bis Xn ]( func_ds(x) ) - s) / func_ds(Xn)
Und genau das machen wir in folgender Funktion:
/* Nähert den Wert t für
* Integral[0 bis t]( func_ds(x) ) = Value
* an.
* Parameter:
* start: ein möglichst genau geschätzter Wert mit dem die Annäherung begonnen werden soll.
* Value: Zielwert nach obiger Formel.
* depth: Anzahl der Iterationen (bzw. um genau zu sein der Rekursionen) je höher dieser Wert desto genauer das Ergebnis
* sections: Wird an NIntegrate weitergereicht, je höher dieser Wert desto genauer das Ergebnis
*/
double FindValue( double start, double Value, int depth, int sections )
{
double newval;
double f = func_ds( start );
if( depth <= 0 )
return start;
// verhindert Division durch 0. Extrem kleine Werte _könnten_ auch problematisch sein.
if( f < 0.0000001 && f > -0.0000001)
{
if( f >= 0.0f )
newval = start - (NIntegrate( 0.0, start, sections ) - Value);
else
newval = start + (NIntegrate( 0.0, start, sections ) - Value);
}
else
{
// die Unterscheidung ob start > 0 ist wird bereits von NIntegrate durchgeführt
newval = start - (NIntegrate( 0.0, start, sections ) - Value) / f;
}
return FindValue( newval, Value, --depth, sections );
}
Nun noch das ein oder andere Beispiel wie wir diese Funktionen verwenden:
/* Beispielshafte Verwendung der Funktionen */
void main()
{
double FullKurveLength = NIntegrate( 0.0, 1.0, 100 );
double TforS;
double KurveLength;
printf( "Die gesamte Kurvenlaenge (von Zeitpunkt 0 bis 1) betraegt ziemlich genau: %f\n", FullKurveLength );
printf( "\n" );
/* Parameter:
* a = 0.0: Wir möchten den zurückgelegten Weg angefangen von Zeitpunkt 0.0
* b = 0.5: Wir möchten den zurückgelegten Weg bis zum Zeitpunkt 0.5, also von 0.0 bis 0.5
* sections = 10: liefert wahrscheinlich ein eher ungenaues Ergebnis.
*/
KurveLength = NIntegrate( 0.0, 0.5, 10 );
printf( "Ungeneau: in der haelfte der Zeit wurde %f Weg zurueck gelegt.\n", KurveLength );
KurveLength = NIntegrate( 0.0, 0.5, 20 );
printf( "Etwas geneauer: in der haelfte der Zeit wurde %f Weg zurueck gelegt.\n", KurveLength );
KurveLength = NIntegrate( 0.0, 0.5, 100 );
printf( "Recht geneau: in der haelfte der Zeit wurde %f Weg zurueck gelegt.\n", KurveLength );
printf( "\n" );
/* Parameter:
* start = 0.5: wir schätzen das der halbe Weg zum Zeitpunkt 0.5 zurück gelegt wurde
* Value = FullKurveLength * 0.5: wir möchten wissen zu welchem Zeitpunkt der halbe Weg zurück gelegt wurde
* depth & sections = 0: liefert wahrscheinlich ein eher ungenaues Ergebnis.
*/
TforS = FindValue( 0.5, FullKurveLength * 0.5, 5, 10 );
printf( "Ungenau: zum Zeitpunkt %f wurde der halbe Weg zurueck gelegt.\n", TforS );
TforS = FindValue( 0.5, FullKurveLength * 0.5, 10, 20 );
printf( "Etwas genauer: zum Zeitpunkt %f wurde der halbe Weg zurueck gelegt.\n", TforS );
TforS = FindValue( 0.5, FullKurveLength * 0.5, 50, 100 );
printf( "Recht genau: zum Zeitpunkt %f wurde der halbe Weg zurueck gelegt.\n", TforS );
};
Als ausgabe dieses Tests erhalten wir:
Die gesamte Kurvenlaenge (von Zeitpunkt 0 bis 1) betraegt ziemlich genau: 9.201214
Ungeneau: in der haelfte der Zeit wurde 5.582572 Weg zurueck gelegt. Etwas geneauer: in der haelfte der Zeit wurde 5.558352 Weg zurueck gelegt. Recht geneau: in der haelfte der Zeit wurde 5.550576 Weg zurueck gelegt.
Ungenau: zum Zeitpunkt 0.376217 wurde der halbe Weg zurueck gelegt. Etwas genauer: zum Zeitpunkt 0.378924 wurde der halbe Weg zurueck gelegt. Recht genau: zum Zeitpunkt 0.379795 wurde der halbe Weg zurueck gelegt.
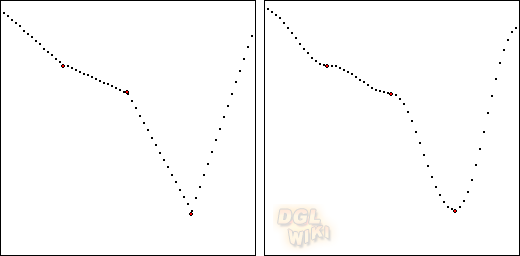
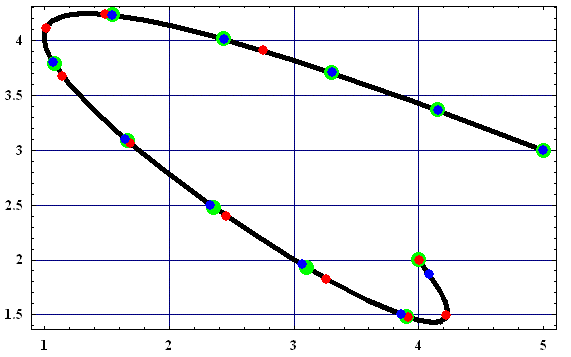
Wir können uns nun auch die Zeitpunkte ausrechnen an denen 10%, 20%, ... des Weges zurück gelegt wurde und uns die Punkte auf der Kurve einzeichnen um auch einen visuelleren Vergleich zu erhalten:
Rot: Die Punkte zu den Zeitpunkten 0.0, 0.1, 0.2, ..., 0.9, 1.0
Blau: Die Punkte zu denen 0%, 10%, 20%, ..., 90%, 100% des Weges zurück gelegt wurde angenähert durch FindValue(...) mit depth = 5 und sections = 10
Grün: Die Punkte zu denen 0%, 10%, 20%, ..., 90%, 100% des Weges zurück gelegt wurde angenähert durch FindValue(...) mit depth = 50 und sections = 100
Gut zu erkennen ist auf diesem Bild auch, dass 10 Unterteilungen für einen das Integrieren von 0 bis 0.1 noch ganz gute Ergebnisse liefert, jedoch bei einem Wertebereich von 0 bis 1 schon ziemlich ungenau wird, somit macht es durchaus Sinn die Anzahl der Unterteilungen auch abhängig von der Größe des Bereiches zu machen.