Tutorial Charakteranimation: Unterschied zwischen den Versionen
(Abschnitt Animation weiterbearbeitet) |
K (→Schlusswort: Kategorie Tutorial eingetragen) |
||
| (26 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
| − | |||
| − | |||
==Einleitung== | ==Einleitung== | ||
In diesem Tutorial möchte ich euch beibringen, wie man starre [[Mesh]]es lebendig erscheinen lässt, indem man sie bewegt. Und zwar wollen wir sie nicht nur verschieben und drehen, sondern richtig animieren, also verformen. Ein sicherer Umgang mit [[Matrizen]], [[VBO]]s und [[Shader]]n wird hier vorausgesetzt. | In diesem Tutorial möchte ich euch beibringen, wie man starre [[Mesh]]es lebendig erscheinen lässt, indem man sie bewegt. Und zwar wollen wir sie nicht nur verschieben und drehen, sondern richtig animieren, also verformen. Ein sicherer Umgang mit [[Matrizen]], [[VBO]]s und [[Shader]]n wird hier vorausgesetzt. | ||
| Zeile 11: | Zeile 8: | ||
Woraus besteht also ein Skelett? Aus Gelenken ('''Joints''') und Knochen ('''Bones'''). In der Grafikprogrammierung hat es sich bewährt, Skelette hierarchisch aufzubauen. Das heißt, es gibt genau ein Supergelenk, das keinem anderen Gelenk untergeordnet ist. Dieses Gelenk wird auch Wurzel genannt, denn in der Informatik würde man sagen, das Skelett ist ein [https://de.wikipedia.org/wiki/Baum_%28Graphentheorie%29 Baum]. Das Wurzelgelenk besitzt untergeordnete Gelenke (Kinder), die mit jeweils einem Knochen mit ihm verbunden sind. Dreht man nun das Wurzelgelenk, so drehen sich alle untergeordneten Knochen und Gelenke (und deren Kinder) mit. Dies entspricht der Realität: Wenn du deinen Arm hebst, d.h. dein Schultergelenk drehst, bewegen sich das Ellenbogen- und Handgelenk, sowie alle Knochen der Hand entsprechend mit. | Woraus besteht also ein Skelett? Aus Gelenken ('''Joints''') und Knochen ('''Bones'''). In der Grafikprogrammierung hat es sich bewährt, Skelette hierarchisch aufzubauen. Das heißt, es gibt genau ein Supergelenk, das keinem anderen Gelenk untergeordnet ist. Dieses Gelenk wird auch Wurzel genannt, denn in der Informatik würde man sagen, das Skelett ist ein [https://de.wikipedia.org/wiki/Baum_%28Graphentheorie%29 Baum]. Das Wurzelgelenk besitzt untergeordnete Gelenke (Kinder), die mit jeweils einem Knochen mit ihm verbunden sind. Dreht man nun das Wurzelgelenk, so drehen sich alle untergeordneten Knochen und Gelenke (und deren Kinder) mit. Dies entspricht der Realität: Wenn du deinen Arm hebst, d.h. dein Schultergelenk drehst, bewegen sich das Ellenbogen- und Handgelenk, sowie alle Knochen der Hand entsprechend mit. | ||
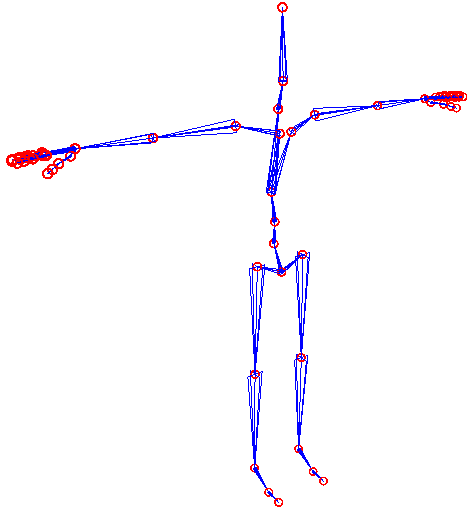
| − | {{Hinweis|Das für die Animation benötigte Skelett muss bei weitem nicht so detailliert sein, wie das reale menschliche Skelett. Mit 64 Joints (inklusive Finger) kann man bereits gute Ergebnisse erzielen.}}<br> | + | {{Hinweis|Das für die Animation benötigte Skelett muss bei weitem nicht so detailliert sein, wie das reale menschliche Skelett. Mit 64 Joints (inklusive Finger) kann man bereits gute Ergebnisse erzielen. Das hier abgebildete Skelett hat 65 Joints, wobei man sich die Spitzen der Finger und Füße noch sparen könnte. (Sie dienen hier nur dazu, die äußersten Knochen zu visualisieren.)}}<br> |
| + | [[Bild:Skelett_T-Pose.png]] | ||
| + | |||
| + | Mathematisch gesehen können wir ein Gelenk durch eine Rotation, eine Position, um die rotiert wird, und die Menge aller Untergelenke beschreiben. Dadurch werden gleichzeitig auch alle Knochen beschrieben, da diese nichts weiter als die Verbindung zwischen einem Eltern- und Kind-Joint sind. Die Rotation lässt sich auf viele Arten beschreiben, z.B. durch eine 3x3-[[Matrix]] oder ein [[Quaternion]] (wobei letzteres aufgrund der guten Interpolierbarkeit zu empfehlen ist). Die Position beschreibt man am einfachsten durch einen Translationsvektor relativ zum Elternknoten. Die Rotation wird in der Regel auch erstmal relativ zum Elternknoten angegeben. | ||
| + | |||
| + | Die absolute Rotation eines Gelenks erhält man ganz einfach, indem man die absolute Rotation des Elternknotens mit der eigenen relativen multipliziert. Die absolute Rotation des Elternknotens muss man natürlich vorher erst einmal berechnen (es sei denn, der Elternknoten ist die Wurzel). Der aufmerksame Leser merkt schon - es riecht nach Rekursion.<br> | ||
| + | Die absolute Position lässt sich ebenfalls rekursiv berechnen. Man multipliziert die absolute Rotationsmatrix des Elternknotens mit der relativen Position und addiert anschließend die absolute Position des Elternknotens. Beide Berechnungen lassen sich in eine Methode stecken: | ||
| − | + | <source lang=cpp>void ComputeAbsJoint(CJoint& Joint, quat parentRot, vec3 parentPos) | |
| − | < | + | { |
| − | + | Joint.AbsPos = parentRot * Joint.RelPos + parentPos; | |
| + | Joint.AbsRot = parentRot * Joint.RelRot; | ||
| + | for(int i=0; i<Joint.numberOfChildren; ++i) | ||
| + | { | ||
| + | ComputeAbsJoint(Joint.Child[i], Joint.AbsRot, Joint.AbsPos); | ||
| + | } | ||
| + | }</source> | ||
| + | ''Joint'' ist also eine Instanz vom Typ ''CJoint'' wird der Funktion [https://de.wikipedia.org/wiki/Call_by_reference per-reference] übergeben. ''Joint.Child'' ist ein Array von Joints. | ||
| + | ''quat'' ist der Typ für ein Quaternion. Hier könnte man wie gesagt auch eine Matrix (''mat3'') oder alles andere nehmen, was in der Lage ist, eine Rotation zu speichern und multipliziert (verkettet) zu werden. | ||
| − | + | Ich hoffe, der Code ist für Programmierer jeder Sprache verständlich :-). | |
| − | |||
==Die Animation== | ==Die Animation== | ||
| Zeile 34: | Zeile 44: | ||
<source lang=cpp>KeyFrames[k].time < time <= KeyFrames[k+1].time</source> | <source lang=cpp>KeyFrames[k].time < time <= KeyFrames[k+1].time</source> | ||
| − | Das endgültige Skelett können wir nun durch die [[Interpolation]] der KeyFrames k und k+1 (Vorsicht vor Überlauf!) berechnen. Der zur Interpolation nötige Faktor ''f'' lässt sich mit<source lang=cpp>f = (time - KeyFrames[k].time) / (KeyFrames[k+1].time - KeyFrames[k].time)</source>berechnen. ''f'' entspricht z.B. dem letzten Parameter der GLSL-Funktion [[Tutorial_glsl#Standardfunktionen|mix]]. | + | Das endgültige Skelett können wir nun durch die [[Interpolation]] der KeyFrames k und k+1 (Vorsicht vor Überlauf!) berechnen. Der zur Interpolation nötige Faktor ''f'' lässt sich mit<source lang=cpp>f = (time - KeyFrames[k].time) / (KeyFrames[k+1].time - KeyFrames[k].time)</source>berechnen. ''f'' entspricht z.B. dem letzten Parameter der GLSL-Funktion [[Tutorial_glsl#Standardfunktionen|mix]]. Um schöne Ergebnisse zu erzielen, sollte man jedoch etwas weicheres als lineare Interpolation verwenden, z.B. die [https://de.wikipedia.org/wiki/Hermiteinterpolation Hermiteinterpolation]. |
==Skinning== | ==Skinning== | ||
| − | Schön und gut, wir wissen jetzt, was ein Skelett ist und wie man es | + | Schön und gut, wir wissen jetzt, was ein Skelett ist und wie man es animiert. Doch was ändert das am Mesh? Schließlich wollen wir in der Endanwendung ja nichts mehr vom Skelett sehen. Offensichtlich benötigen wir eine Möglichkeit, die Vertices des Meshs mit dem Skelett zu verbinden. Das ist nicht schwierig: Wir ordnen jedem Vertex die Nummer (einen Integer) des Gelenks zu, das ihn beeinflusst. Das ist nicht der Weisheit letzter Schluss, aber sehr einfach und genau das Richtige, wenn man überhaupt erstmal ein Ergebnis sehen will. |
| + | |||
| + | ===Transformation der Positionen=== | ||
| + | Wir wissen nun von einem Vertex, welche Position er in der Standardpose (bei Menschen i.d.R. T-Pose) hat und von welchem Gelenk er beeinflusst wird. Um zu verstehen, was mit den Vertices bei der Animation passiert, betrachten wir beispielhaft den hier in grün markierten Vertex:<br> | ||
| + | [[Bild:arm2_tpose2.png]]<br> | ||
| + | Er ist dem Ellenbogen-Gelenk (roter Kreis links neben ihm) des linken (aus unserer Sicht rechten) Arms zugeordnet. | ||
| + | |||
| + | Als erstes berechnen wir den Verbindungsvektor vom Joint in T-Pose zum Vertex: | ||
| + | Diff = VPos - TPoseJoint.AbsPos | ||
| + | Diesen Verbindungsvektor rotieren wir nun entsprechend der aktuellen Ausrichtung des Joints. Das heißt, wir wenden die absolute Rotationsmatrix bzw. das Quaternion des Joints an: | ||
| + | Rotated = Joint.AbsRot * Diff | ||
| + | Den erhaltenen Rotationsvektor addieren wir schließlich auf die absolute Position des Joints im animierten Skelett; | ||
| + | Result = Joint.AbsPos + Rotated | ||
| + | Die fertige Position entspricht dem, was wir hier sehen:<br> | ||
| + | [[Bild:arm2_moved2.png]]<br> | ||
| + | Diese drei Schritte solltest du unbedingt nachvollzogen und verstanden haben, bevor du dich an die Implementierung machst. Man beachte v.a. den Unterschied zwischen TPoseJoint (enthält Position und Rotation in Standardpose, also unbewegt wie im ersten Bild) und Joint (das Ergebnis der KeyFrame-Interpolation, zweites Bild). | ||
| + | |||
| + | ===Transformation von Normalen=== | ||
| + | Ein [[Vertex]] besteht nicht nur aus einer Position. [[Normale]]n und [[TBN Matrix|andere Vektoren]], die lediglich eine Richtung und keine Position enthalten, brauchen natürlich nicht wie Positionsvektoren transliert werden. Auf sie wird nur die Rotation (Schritt 2) angewandt. | ||
| + | |||
| + | ===Transformation von Texturkoordinaten=== | ||
| + | "Hö? Wieso müssen Texturkoordinaten transformiert werden?" Wenn du dich das beim Lesen der Überschrift dieses Abschnitts gefragt hast, liegst du genau richtig. Texturkoordinaten sind nicht von der Animation betroffen. Dieser Abschnitt ist nur ein Test, ob du bis hierher alles verstanden hast. ;-)<br> | ||
| + | Hier wäre eine gute Stelle, das bisher gelernte zu vertiefen, indem du dich an einer eigener Implementation versuchst. | ||
| + | |||
| + | ==Skinning für Fortgeschrittene== | ||
| + | Im letzten Abschnitt habe ich geschrieben, dass wir jedem Vertex ein Gelenk zuordnen. Wenn es gut aussehen soll, reicht eins allein jedoch nicht aus. Denn was soll man beispielsweise mit einem Vertex machen, der auf der Haut nahe des Handgelenks eines Menschen liegt? Gehört er zum Hand- oder doch zum Unterarmknochen? Die Antwort lautet: beides. Seine Position wird sowohl von der Drehung des Ellenbogens, als auch von der Drehung des Handgelenks beeinflusst. Das heißt, wir müssen jedem Vertex mindestens zwei Gelenke zuordnen. In der Praxis nimmt man oft sogar vier. So werden wir auch im folgenden Verfahren. | ||
| + | |||
| + | Doch nun, da wir festgestellt haben, dass oft kein Knochen alleinigen Einfluss auf einen Vertex hat, müssen wir für jeden der 4 Joints auch noch den Anteil an Einfluss speichern. Dafür hat sich der Begriff '''BoneWeight''' eingebürgert. Ich benutze lieber die Bezeichnung '''JointWeight''', da wir die Transformationen, die wir hiermit gewichten, nicht pro Bone, sondern pro Joint speichern. Das JointWeight hat einen Wert zwischen 0 und 1 und i.d.R. ist es so, dass die Summe aller JointWeights eines Vertex 1 ergibt. Somit kann man ein wenig Speicherplatz sparen, da man das letzte JointWeight jederzeit berechnen kann: | ||
| + | Leztes JointWeight = 1 - (Summe aller anderen JointWeights) | ||
| + | <br> | ||
| + | Die Gewichtung der einzelnen Joints tatsächlich umzusetzen, ist nicht trivial. Um genau zu sein: Es ist wahrscheinlich das schwierigste Problem des ganzen Themas. Es ohne störende Artefakte zu lösen, gelang in der Praxis erst vor einigen Jahren mithilfe höherer Mathematik. Doch nun erstmal die verschiedenen Ansätze der Reihe nach: | ||
| + | |||
| + | ===Matrix-Interpolation=== | ||
| + | Im letzten Abschnitt haben wir gesehen, dass die Transformation eines Vertex (bzw. seiner Position) aus drei Schritten besteht. Erst eine Translation, dann eine Rotation und zum Schluss noch eine Translation. Wer sich ein bisschen mit Matrizen auskennt (und das hatte ich am Anfang des Tutorials vorausgesetzt ;-) ), der weiß, dass man alle drei Transformationen in nur eine Matrix stecken kann. Da scheint es doch naheliegend zu sein, für jeden Joint eine solche Matrix zu bauen: | ||
| + | TransMatrix1.setTranslation(-TPoseJoint.AbsPos); | ||
| + | RotMatrix.setRotation(Joint.AbsRot); | ||
| + | TransMatrix2.setTranslation(Joint.AbsPos); | ||
| + | Matrix = TransMatrix2 * RotMatrix * TransMatrix1; | ||
| + | |||
| + | Da jeder Vertex von 4 Joints beeinflusst wird, warum gewichtet man dann nicht einfach die Matrizen? | ||
| + | finalMatrix = Matrix[JointID[0]] * JointWeight[0] | ||
| + | + Matrix[JointID[1]] * JointWeight[1] | ||
| + | + Matrix[JointID[2]] * JointWeight[2] | ||
| + | + Matrix[JointID[3]] * JointWeight[3]; | ||
| + | finalPos = finalMatrix * VPos; | ||
| + | Leider bringt die Matrix-Interpolation nicht das gewünschte Ergebnis. Dies lässt sich sehr einfach an einem Beispiel nachvollziehen:<br> | ||
| + | Wir nehmen an, ein Vertex wird von zwei Joints zu je 50% beeinflusst (d.h. JointWeight[0] = JointWeight[1] = 0.5 und JointWeight[2] = JointWeight[3] = 0.0). Der eine Joint hat die Identitätsmatrix und der andere eine um 90° um die x-Achse rotierte Identitätsmatrix. Als Mittelung dieser beiden Drehungen würde man eine Rotation um 45° um die x-Achse erwarten. Doch was kommt tatsächlich raus?<br> | ||
| + | [[Bild:matrix_blending_beispiel.png|526px]]<br><br> | ||
| + | Das ist offensichtlich nicht das gleiche wie eine 45°-Rotationsmatrix um die x-Achse:<br> | ||
| + | [[Bild:45grad_um_X_Matrix.png|210px]]<br> | ||
| + | Der interpolierten Matrix ist außerdem noch eine wichtige Eigenschaft verloren gegangen: Wenn man den 3x3-Teil herausschneidet, hat man keine reine Rotationsmatrix mehr. Denn die Länge der letzten beiden Spaltenvektoren ist nicht mehr 1, sondern | ||
| + | sqrt(0² + 0.5² + 0.5²) = sqrt(0.5) = 0.707 | ||
| + | Die Matrix enthält nun also zusätzlich eine unerwünschte Skalierung. Zwar könnte man alle Spaltenvektoren nach dem Blending normalisieren, doch das ist teuer und es gibt viel bessere Lösungen, wie die nächsten Abschnitte zeigen werden. | ||
| + | |||
| + | ===Lineare Vertex-Interpolation=== | ||
| + | Was dagegen schon halbwegs brauchbar ist, ist ein ähnlicher Ansatz namens '''Vertex Blending'''. Man baut wieder die Matrizen wie beim Ansatz eben. Zum Gewichten der Transformation mittelt man nun aber nicht die Matrizen, sondern die mit ihnen transformierten Vektoren: | ||
| + | pos0 = Matrix[JointID[0]] * VPos; | ||
| + | pos1 = Matrix[JointID[1]] * VPos; | ||
| + | pos2 = Matrix[JointID[2]] * VPos; | ||
| + | pos3 = Matrix[JointID[3]] * VPos; | ||
| + | finalPos = pos0 * JointWeight[0] | ||
| + | + pos1 * JointWeight[1] | ||
| + | + pos2 * JointWeight[2] | ||
| + | + pos3 * JointWeight[3]; | ||
| + | Dass dieser Ansatz auch nicht optimal ist, kann man gut an dieser Grafik sehen:<br> | ||
| + | [[Bild:linear vs spherical blending.png|430px]]<br> | ||
| + | Angenommen wir haben zwei Joints, die Einfluss auf einen Vertex haben. Beide Joints rotieren um die selbe Achse (in der Grafik: um den Punkt P0), jedoch verschieden stark. Der erste Joint würde den Vertex an Position ''v0'' bringen und die Transformation mit dem zweiten Joint hätte ''v1'' als Ergebnis. Wenn wir nun den Vertex Blending-Ansatz zum Mitteln der Transformation anwenden, wäre das Ergebnis ''v'''. Das Blending verläuft entlang der oberen gepunkteten Linie. Was man aber in der Regel haben will, ist eine Interpolation des Winkels, sodass das Ergebnis immer ein Punkt auf der Kreislinie ist. Für den Beispiel-Fall, dass die JointWeights jeweils 0.5 sind, wäre das Ergebnis der (idealen) sphärischen Interpolation der Punkt ''P1'' an dem sich die Winkelhalbierende (orange) mit der Kreislinie schneidet. | ||
| + | |||
| + | Je stärker sich die Rotationen zweier Joints unterscheiden, desto größer wird also der Fehler (= Abstand zwischen ''v''' und ''P1'') des linearen Vertex Blending. Dies wird besonders deutlich, wenn z.B. ein menschlicher Charakter seine Hand oder seinen Arm dreht, die dann wie abgeschnürt aussieht. | ||
| + | |||
| + | ===Quaternion + Translationsvektor=== | ||
| + | In [[Quaternion]]en kann man Rotationen speichern und im Gegensatz zu Matrizen lassen sie sich auch sehr gut Interpolieren. Da ihnen aber die Translationsfähigkeit fehlt, benötigt man zusätzlich einen Vektor dafür. Wir möchten erreichen, dass sich ein Vertex wie folgt transformieren lässt: | ||
| + | mixedQuaternion = Quaternion[JointID[0]] * JointWeight[0] | ||
| + | + Quaternion[JointID[1]] * JointWeight[1] | ||
| + | + Quaternion[JointID[2]] * JointWeight[2] | ||
| + | + Quaternion[JointID[3]] * JointWeight[3]; | ||
| + | finalQuaternion = normalize(mixedQuaternion); | ||
| + | finalTranslation = Translation[JointID[0]] * JointWeight[0] | ||
| + | + Translation[JointID[1]] * JointWeight[1] | ||
| + | + Translation[JointID[2]] * JointWeight[2] | ||
| + | + Translation[JointID[3]] * JointWeight[3]; | ||
| + | finalPos = finalQuaternion * VPos + finalTranslation; | ||
| + | |||
| + | Dies ist möglich, aber ein kleines bisschen komplizierter, da wir eigentlich zwei Translationen haben: Eine vor und eine nach der Rotation. Diese müssen wir nun zusammenfassen zu nur einer Translation, die nach der Rotation stattfindet. Dazu wenden wir auf den ersten Translationsvektor einfach die Rotation des Joints an, bevor wir die Summe mit seinem "Kollegen" bilden: | ||
| + | Translation = Quaternion * (-TPoseJoint.AbsPos) + Joint.AbsPos; | ||
| + | Der große Vorteil der Quaternionen gegenüber den voherigen Ansätzen ist wie gesagt die gute Interpolierbarkeit. Wenn man die Quaternionen wie oben gewichtet addiert und das Resultat normalisiert, landet man immer auf der Kreislinie. Zwar entspricht dies nicht ganz der sphärischen Interpolation, aber es gibt einen mathematischen Beweis, der zeigt, dass man nie weiter als 8,15° (Winkel zwischen den beiden orangenen Linien) vom idealen Ergebnis entfernt ist. Dies ist eine obere Grenze für den Fehler - in der Praxis liegt man meistens noch deutlich darunter.<br> | ||
| + | [[Bild:quaternion vs spherical blending.png|430px]] | ||
| + | |||
| + | ===Dual Quaternions=== | ||
| + | Beim [[Dual Quaternion]]-Ansatz geht man im Prinzip den gleichen Weg, wie bei Matrizen. Man erzeugt also zwei Dual Quaternions für Translation und eines für Rotation. Via Multiplikation fasst man alle drei Transformationen in einem Dual Quaternion zusammen. Auf diese Weise erzeugt man für jeden Joint ein Dual Quaternion. Das Tolle an Dual Quaternions ist jedoch, dass man sie im Gegensatz zu Matrizen ganz hervorragend (genau wie gewöhnliche Quaternionen) interpolieren kann. Die Vertex-Transformation sieht also so aus: | ||
| + | finalDQ = DualQuat[JointID[0]] * JointWeight[0] | ||
| + | + DualQuat[JointID[1]] * JointWeight[1] | ||
| + | + DualQuat[JointID[2]] * JointWeight[2] | ||
| + | + DualQuat[JointID[3]] * JointWeight[3]; | ||
| + | finalDQ.normalize(); | ||
| + | finalPos = finalDQ * VPos; | ||
| + | Was genau die letzten beiden Zeilen machen, ist im Artikel [[Dual Quaternion]] erklärt. | ||
| + | Da Normalenvektoren der Translationsteil des Dual Quaternions nicht betrifft, wird auf ihn nur das nicht-duale Quaternion angewandt: | ||
| + | finalNormal = finalDQ.real * Normal | ||
| + | |||
| + | Dual Quaternion-Skinning bietet neben der schönen Interpolation den Vorteil, dass ein Dual Quaternion nur halb so viel Platz benötigt wie eine Matrix. Leider ist es jedoch nicht so schnell wie der Vertex-Blending Ansatz und die Mathematik dahinter ist schwer in aller Tiefe verstehen. | ||
| + | |||
| + | ==Implementation im Vertexshader== | ||
| + | Ein Model hat in der Regel mehrere tausend Vertices und da man in Videospielen meistens auch noch mehrere animierte Models gleichzeitig sieht, müssen schnell mal einige zehntausend Vertices pro Frame per skeletaler Animation transformiert werden. Selbst heutige CPUs stoßen da schonmal an Grenzen - vor allem, wenn sie auch noch andere Aufgaben erledigen soll. Die benötigte Rechenleistung lässt sich nur durch Parallelisierung bereitstellen. Und - Quizfrage: Welcher Prozessor im PC arbeitet extrem parallel? Na...?<br> | ||
| + | Ja, richtig: Die GPU. Also nutzen wir doch deren Shader-Rechenwerke für die Transformation. Genauer gesagt, werden wir den Vertexshader dafür nutzen: | ||
| + | <source lang=glsl>#version 330 | ||
| + | const int g_JointsMax = 64; | ||
| + | |||
| + | uniform mat4 u_ModelViewProjectionMatrix; | ||
| + | uniform mat3 u_NormalMatrix; | ||
| + | uniform vec4 u_DualQuats[g_JointsMax*2]; | ||
| + | |||
| + | in vec3 inPos; | ||
| + | in vec3 inNormal; | ||
| + | in vec2 inTexCoord; | ||
| + | in vec4 inJointWeight; | ||
| + | in uvec4 inJointID; | ||
| + | |||
| + | out vec3 vf_Normal; | ||
| + | out vec2 vf_TexCoord; | ||
| + | |||
| + | void NormalizeDualQuat(inout vec4 real, inout vec4 dual) | ||
| + | { | ||
| + | real = normalize(real); | ||
| + | dual -= real * dot(real, dual); | ||
| + | } | ||
| + | void GetDualQuat(out vec4 real, out vec4 dual) | ||
| + | { | ||
| + | real = u_DualQuats[inJointID[0]*2u] * inJointWeight[0] | ||
| + | + u_DualQuats[inJointID[1]*2u] * inJointWeight[1] | ||
| + | + u_DualQuats[inJointID[2]*2u] * inJointWeight[2] | ||
| + | + u_DualQuats[inJointID[3]*2u] * inJointWeight[3]; | ||
| + | dual = u_DualQuats[inJointID[0]*2u +1u] * inJointWeight[0] | ||
| + | + u_DualQuats[inJointID[1]*2u +1u] * inJointWeight[1] | ||
| + | + u_DualQuats[inJointID[2]*2u +1u] * inJointWeight[2] | ||
| + | + u_DualQuats[inJointID[3]*2u +1u] * inJointWeight[3]; | ||
| + | |||
| + | NormalizeDualQuat(real, dual); | ||
| + | } | ||
| + | vec3 TransformPosition(vec3 v, vec4 real, vec4 dual) | ||
| + | { | ||
| + | vec3 term1 = cross(real.xyz, cross(real.xyz, v) + real.w*v); | ||
| + | v += 2.0 * (term1 + real.w*dual.xyz - dual.w*real.xyz + cross(real.xyz, dual.xyz)); | ||
| + | return v; | ||
| + | } | ||
| + | vec3 TransformNormal(vec3 n, vec4 quat) | ||
| + | { | ||
| + | n += 2.0 * cross(quat.xyz, cross(quat.xyz, n) + quat.w*n); | ||
| + | return n; | ||
| + | } | ||
| + | |||
| + | void main(void) | ||
| + | { | ||
| + | vec3 skinnedPos = inPos; | ||
| + | vec3 skinnedNormal = inNormal; | ||
| + | |||
| + | // dual quaternion skinning | ||
| + | if(inJointWeight[0] > 0.0) | ||
| + | { | ||
| + | vec4 real, dual; | ||
| + | GetDualQuat(real, dual); | ||
| + | skinnedPos = TransformPosition(inPos, real, dual); | ||
| + | skinnedNormal = TransformNormal(inNormal, real); | ||
| + | } | ||
| + | |||
| + | // usual transformation | ||
| + | vf_TexCoord = inTexCoord; | ||
| + | vf_Normal = normalize(u_NormalMatrix * skinnedNormal); | ||
| + | gl_Position = u_ModelViewProjectionMatrix * vec4(skinnedPos, 1.0); | ||
| + | } | ||
| + | </source> | ||
| + | Dieser Vertexshader implementiert DualQuaternion-Skinning. Bei Vertices, die nicht geskinnt werden sollen, setzt man einfach die erste Komponente des Vertexattributs ''inJointWeight'' auf 0. Wie man sieht, ist die Implementierung sehr nahe am Pseudocode der Beschreibung des Ansatzes oben. Es sollte daher leicht fallen, auch die anderen Verfahren im Vertexshader zu implementieren. | ||
| + | |||
| + | Die Transformation mittels Quaternion und Translationsvektor würde z.B. so aussehen: | ||
| + | <source lang=glsl>vec3 TransformPosition(vec3 v, vec4 quat, vec3 trans) | ||
| + | { | ||
| + | return TransformNormal(v, quat) + trans; | ||
| + | }</source> | ||
| + | |||
| + | ==Schlusswort== | ||
| + | Das war es auch schon mit meinem ersten Wiki-Artikel in der Kategorie Tutorial. Ich hoffe, die Erklärungen waren verständlich und nicht zu trocken. Falls nicht, gibt es immer noch unser [http://www.delphigl.com/forum/index.php Forum], das auf Feedback und Fragen wartet. | ||
| − | + | Natürlich kann man die in diesem Tutorial beschriebene Animationstechnik noch erweitern. Sinnvoll wäre z.B., wenn ein Charakter mehrere Animationen gleichzeitig ausführen kann (manche Animationen betreffen ja nur Teile des Skeletts) oder ein sanftes Überblenden vom Kriechen zum Gehen und vom Gehen zum Rennen. | |
| − | |||
| − | + | Für diejenigen, die noch tiefer in die Materie der Charakteranimation einsteigen wollen, gibt es noch eine Menge anderer interessanter Techniken zu erlernen. Mittels inverser Kinematik kann man beispielsweise berechnen, wie sich der Rest des Skeletts bewegen muss, um einen bestimmten Joint eines Charakters an eine bestimmte Position zu bekommen. Damit lassen sich u.a. automatisch an die Umgebung angepasste Animationen erzeugen. | |
| − | + | Wenn du eine coole Technik erlernt hast, zu der es noch kein Tutorial auf DGL gibt, würde es (nicht nur) mich natürlich freuen, wenn du die Plattform nutzt, dein Wissen zu teilen. In diesem Sinne: Frohes Schaffen! | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Kategorie:Tutorial|Charakteranimation]] | |
| − | |||
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 2. März 2014, 23:18 Uhr
Inhaltsverzeichnis
Einleitung
In diesem Tutorial möchte ich euch beibringen, wie man starre Meshes lebendig erscheinen lässt, indem man sie bewegt. Und zwar wollen wir sie nicht nur verschieben und drehen, sondern richtig animieren, also verformen. Ein sicherer Umgang mit Matrizen, VBOs und Shadern wird hier vorausgesetzt.
Das Skelett
Es gibt verschiedene Ansätze, ein Mesh durch Animation zu verformen. Meistens möchte man in Computerspielen Menschen oder Tiere (oder etwas, das ihnen ähnelt) animieren, die sich nur sehr eingeschränkt verformen können - nämlich so, wie es ihr Skelett zulässt. Daher kommt meistens Skelett-basierte Animation zum Einsatz. Sich bewegene Maschinen oder Roboter sind meistens noch beschränkter in ihrer Bewegegungsfreiheit, sodass sich deren Animationen ebenfalls mittels eines Skeletts realisieren lässt. Die Idee ist einfach: Man speichert für einen Charakter nur, wie sich das Skelett bei einer Animation bewegt. Das Skelett besteht aus deutlich weniger Teilen, als das Mesh (die Haut) Vertices hat. Die Auswirkungen auf die Vertices selbst werden erst während des Renderns in Echtzeit berechnet. Durch dieses Verfahren wird eine Menge Speicherplatz, aber auch Aufwand beim Erstellen und Bearbeiten von Animationen gespart.
Woraus besteht also ein Skelett? Aus Gelenken (Joints) und Knochen (Bones). In der Grafikprogrammierung hat es sich bewährt, Skelette hierarchisch aufzubauen. Das heißt, es gibt genau ein Supergelenk, das keinem anderen Gelenk untergeordnet ist. Dieses Gelenk wird auch Wurzel genannt, denn in der Informatik würde man sagen, das Skelett ist ein Baum. Das Wurzelgelenk besitzt untergeordnete Gelenke (Kinder), die mit jeweils einem Knochen mit ihm verbunden sind. Dreht man nun das Wurzelgelenk, so drehen sich alle untergeordneten Knochen und Gelenke (und deren Kinder) mit. Dies entspricht der Realität: Wenn du deinen Arm hebst, d.h. dein Schultergelenk drehst, bewegen sich das Ellenbogen- und Handgelenk, sowie alle Knochen der Hand entsprechend mit.
Mathematisch gesehen können wir ein Gelenk durch eine Rotation, eine Position, um die rotiert wird, und die Menge aller Untergelenke beschreiben. Dadurch werden gleichzeitig auch alle Knochen beschrieben, da diese nichts weiter als die Verbindung zwischen einem Eltern- und Kind-Joint sind. Die Rotation lässt sich auf viele Arten beschreiben, z.B. durch eine 3x3-Matrix oder ein Quaternion (wobei letzteres aufgrund der guten Interpolierbarkeit zu empfehlen ist). Die Position beschreibt man am einfachsten durch einen Translationsvektor relativ zum Elternknoten. Die Rotation wird in der Regel auch erstmal relativ zum Elternknoten angegeben.
Die absolute Rotation eines Gelenks erhält man ganz einfach, indem man die absolute Rotation des Elternknotens mit der eigenen relativen multipliziert. Die absolute Rotation des Elternknotens muss man natürlich vorher erst einmal berechnen (es sei denn, der Elternknoten ist die Wurzel). Der aufmerksame Leser merkt schon - es riecht nach Rekursion.
Die absolute Position lässt sich ebenfalls rekursiv berechnen. Man multipliziert die absolute Rotationsmatrix des Elternknotens mit der relativen Position und addiert anschließend die absolute Position des Elternknotens. Beide Berechnungen lassen sich in eine Methode stecken:
void ComputeAbsJoint(CJoint& Joint, quat parentRot, vec3 parentPos)
{
Joint.AbsPos = parentRot * Joint.RelPos + parentPos;
Joint.AbsRot = parentRot * Joint.RelRot;
for(int i=0; i<Joint.numberOfChildren; ++i)
{
ComputeAbsJoint(Joint.Child[i], Joint.AbsRot, Joint.AbsPos);
}
}
Joint ist also eine Instanz vom Typ CJoint wird der Funktion per-reference übergeben. Joint.Child ist ein Array von Joints. quat ist der Typ für ein Quaternion. Hier könnte man wie gesagt auch eine Matrix (mat3) oder alles andere nehmen, was in der Lage ist, eine Rotation zu speichern und multipliziert (verkettet) zu werden.
Ich hoffe, der Code ist für Programmierer jeder Sprache verständlich :-).
Die Animation
Die Animation besteht nun aus einer Folge von KeyFrames. Ein KeyFrame beschreibt den Zustand des Skeletts zu einer bestimmten Zeit. Für jeden KeyFrame werden also gespeichert:
- Die Zeit
- Die Rotation jedes Joints (relativ zum Eltern-Joint)
- Die Position jedes Joints (ebenfalls relativ zum Eltern-Joint)
Die KeyFrames werden nach der Zeit sortiert in einem Array gespeichert. Zwischen den KeyFrames kann man interpolieren und somit auch Zustände des Skeletts zwischen zwei KeyFrames berechnen. Das macht man sich bei der Animation zu nutze.
Man benötigt also eine Zeitvariable time (vom Typ float), die man beim Starten der Animation auf 0 setzt. In jedem Frame (hier ist nicht KeyFrame gemeint, sondern Frame wie in Framerate) erhöht man time um die im letzten Frame vergangene Zeit. Nun sucht man den KeyFrame mit der größten Zeit, die noch kleiner ist als time. Bei der Suche sollte man ausnutzen, dass man die KeyFrames nach der Zeit sortiert hat. Es wäre unnötig langsam, jeden einzelnen KeyFrame der Liste abzuklappern. Besser wäre
- sich das Suchergebnis vom letzten Frame zu merken und die Suche ab dort zu starten oder
- eine binäre Suche oder
- eine proportionale Suche.
Die Suche liefert uns den Index k des gesuchten KeyFrames, so dass gilt:
KeyFrames[k].time < time <= KeyFrames[k+1].time
f = (time - KeyFrames[k].time) / (KeyFrames[k+1].time - KeyFrames[k].time)
Skinning
Schön und gut, wir wissen jetzt, was ein Skelett ist und wie man es animiert. Doch was ändert das am Mesh? Schließlich wollen wir in der Endanwendung ja nichts mehr vom Skelett sehen. Offensichtlich benötigen wir eine Möglichkeit, die Vertices des Meshs mit dem Skelett zu verbinden. Das ist nicht schwierig: Wir ordnen jedem Vertex die Nummer (einen Integer) des Gelenks zu, das ihn beeinflusst. Das ist nicht der Weisheit letzter Schluss, aber sehr einfach und genau das Richtige, wenn man überhaupt erstmal ein Ergebnis sehen will.
Transformation der Positionen
Wir wissen nun von einem Vertex, welche Position er in der Standardpose (bei Menschen i.d.R. T-Pose) hat und von welchem Gelenk er beeinflusst wird. Um zu verstehen, was mit den Vertices bei der Animation passiert, betrachten wir beispielhaft den hier in grün markierten Vertex:
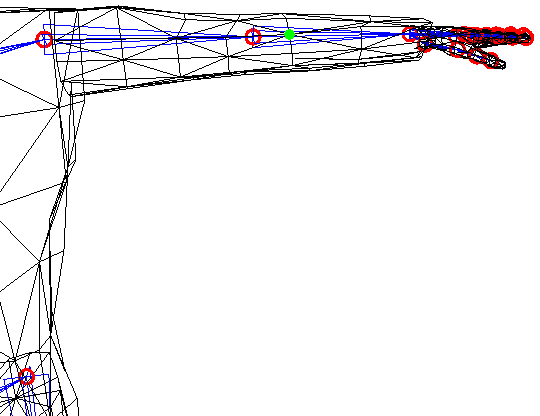
Er ist dem Ellenbogen-Gelenk (roter Kreis links neben ihm) des linken (aus unserer Sicht rechten) Arms zugeordnet.
Als erstes berechnen wir den Verbindungsvektor vom Joint in T-Pose zum Vertex:
Diff = VPos - TPoseJoint.AbsPos
Diesen Verbindungsvektor rotieren wir nun entsprechend der aktuellen Ausrichtung des Joints. Das heißt, wir wenden die absolute Rotationsmatrix bzw. das Quaternion des Joints an:
Rotated = Joint.AbsRot * Diff
Den erhaltenen Rotationsvektor addieren wir schließlich auf die absolute Position des Joints im animierten Skelett;
Result = Joint.AbsPos + Rotated
Die fertige Position entspricht dem, was wir hier sehen:
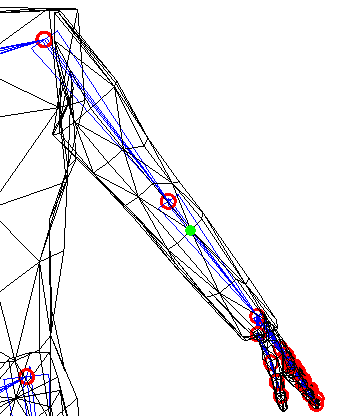
Diese drei Schritte solltest du unbedingt nachvollzogen und verstanden haben, bevor du dich an die Implementierung machst. Man beachte v.a. den Unterschied zwischen TPoseJoint (enthält Position und Rotation in Standardpose, also unbewegt wie im ersten Bild) und Joint (das Ergebnis der KeyFrame-Interpolation, zweites Bild).
Transformation von Normalen
Ein Vertex besteht nicht nur aus einer Position. Normalen und andere Vektoren, die lediglich eine Richtung und keine Position enthalten, brauchen natürlich nicht wie Positionsvektoren transliert werden. Auf sie wird nur die Rotation (Schritt 2) angewandt.
Transformation von Texturkoordinaten
"Hö? Wieso müssen Texturkoordinaten transformiert werden?" Wenn du dich das beim Lesen der Überschrift dieses Abschnitts gefragt hast, liegst du genau richtig. Texturkoordinaten sind nicht von der Animation betroffen. Dieser Abschnitt ist nur ein Test, ob du bis hierher alles verstanden hast. ;-)
Hier wäre eine gute Stelle, das bisher gelernte zu vertiefen, indem du dich an einer eigener Implementation versuchst.
Skinning für Fortgeschrittene
Im letzten Abschnitt habe ich geschrieben, dass wir jedem Vertex ein Gelenk zuordnen. Wenn es gut aussehen soll, reicht eins allein jedoch nicht aus. Denn was soll man beispielsweise mit einem Vertex machen, der auf der Haut nahe des Handgelenks eines Menschen liegt? Gehört er zum Hand- oder doch zum Unterarmknochen? Die Antwort lautet: beides. Seine Position wird sowohl von der Drehung des Ellenbogens, als auch von der Drehung des Handgelenks beeinflusst. Das heißt, wir müssen jedem Vertex mindestens zwei Gelenke zuordnen. In der Praxis nimmt man oft sogar vier. So werden wir auch im folgenden Verfahren.
Doch nun, da wir festgestellt haben, dass oft kein Knochen alleinigen Einfluss auf einen Vertex hat, müssen wir für jeden der 4 Joints auch noch den Anteil an Einfluss speichern. Dafür hat sich der Begriff BoneWeight eingebürgert. Ich benutze lieber die Bezeichnung JointWeight, da wir die Transformationen, die wir hiermit gewichten, nicht pro Bone, sondern pro Joint speichern. Das JointWeight hat einen Wert zwischen 0 und 1 und i.d.R. ist es so, dass die Summe aller JointWeights eines Vertex 1 ergibt. Somit kann man ein wenig Speicherplatz sparen, da man das letzte JointWeight jederzeit berechnen kann:
Leztes JointWeight = 1 - (Summe aller anderen JointWeights)
Die Gewichtung der einzelnen Joints tatsächlich umzusetzen, ist nicht trivial. Um genau zu sein: Es ist wahrscheinlich das schwierigste Problem des ganzen Themas. Es ohne störende Artefakte zu lösen, gelang in der Praxis erst vor einigen Jahren mithilfe höherer Mathematik. Doch nun erstmal die verschiedenen Ansätze der Reihe nach:
Matrix-Interpolation
Im letzten Abschnitt haben wir gesehen, dass die Transformation eines Vertex (bzw. seiner Position) aus drei Schritten besteht. Erst eine Translation, dann eine Rotation und zum Schluss noch eine Translation. Wer sich ein bisschen mit Matrizen auskennt (und das hatte ich am Anfang des Tutorials vorausgesetzt ;-) ), der weiß, dass man alle drei Transformationen in nur eine Matrix stecken kann. Da scheint es doch naheliegend zu sein, für jeden Joint eine solche Matrix zu bauen:
TransMatrix1.setTranslation(-TPoseJoint.AbsPos); RotMatrix.setRotation(Joint.AbsRot); TransMatrix2.setTranslation(Joint.AbsPos); Matrix = TransMatrix2 * RotMatrix * TransMatrix1;
Da jeder Vertex von 4 Joints beeinflusst wird, warum gewichtet man dann nicht einfach die Matrizen?
finalMatrix = Matrix[JointID[0]] * JointWeight[0]
+ Matrix[JointID[1]] * JointWeight[1]
+ Matrix[JointID[2]] * JointWeight[2]
+ Matrix[JointID[3]] * JointWeight[3];
finalPos = finalMatrix * VPos;
Leider bringt die Matrix-Interpolation nicht das gewünschte Ergebnis. Dies lässt sich sehr einfach an einem Beispiel nachvollziehen:
Wir nehmen an, ein Vertex wird von zwei Joints zu je 50% beeinflusst (d.h. JointWeight[0] = JointWeight[1] = 0.5 und JointWeight[2] = JointWeight[3] = 0.0). Der eine Joint hat die Identitätsmatrix und der andere eine um 90° um die x-Achse rotierte Identitätsmatrix. Als Mittelung dieser beiden Drehungen würde man eine Rotation um 45° um die x-Achse erwarten. Doch was kommt tatsächlich raus?
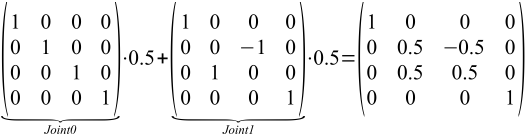
Das ist offensichtlich nicht das gleiche wie eine 45°-Rotationsmatrix um die x-Achse:

Der interpolierten Matrix ist außerdem noch eine wichtige Eigenschaft verloren gegangen: Wenn man den 3x3-Teil herausschneidet, hat man keine reine Rotationsmatrix mehr. Denn die Länge der letzten beiden Spaltenvektoren ist nicht mehr 1, sondern
sqrt(0² + 0.5² + 0.5²) = sqrt(0.5) = 0.707
Die Matrix enthält nun also zusätzlich eine unerwünschte Skalierung. Zwar könnte man alle Spaltenvektoren nach dem Blending normalisieren, doch das ist teuer und es gibt viel bessere Lösungen, wie die nächsten Abschnitte zeigen werden.
Lineare Vertex-Interpolation
Was dagegen schon halbwegs brauchbar ist, ist ein ähnlicher Ansatz namens Vertex Blending. Man baut wieder die Matrizen wie beim Ansatz eben. Zum Gewichten der Transformation mittelt man nun aber nicht die Matrizen, sondern die mit ihnen transformierten Vektoren:
pos0 = Matrix[JointID[0]] * VPos;
pos1 = Matrix[JointID[1]] * VPos;
pos2 = Matrix[JointID[2]] * VPos;
pos3 = Matrix[JointID[3]] * VPos;
finalPos = pos0 * JointWeight[0]
+ pos1 * JointWeight[1]
+ pos2 * JointWeight[2]
+ pos3 * JointWeight[3];
Dass dieser Ansatz auch nicht optimal ist, kann man gut an dieser Grafik sehen:
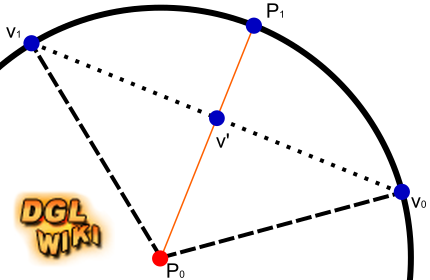
Angenommen wir haben zwei Joints, die Einfluss auf einen Vertex haben. Beide Joints rotieren um die selbe Achse (in der Grafik: um den Punkt P0), jedoch verschieden stark. Der erste Joint würde den Vertex an Position v0 bringen und die Transformation mit dem zweiten Joint hätte v1 als Ergebnis. Wenn wir nun den Vertex Blending-Ansatz zum Mitteln der Transformation anwenden, wäre das Ergebnis v'. Das Blending verläuft entlang der oberen gepunkteten Linie. Was man aber in der Regel haben will, ist eine Interpolation des Winkels, sodass das Ergebnis immer ein Punkt auf der Kreislinie ist. Für den Beispiel-Fall, dass die JointWeights jeweils 0.5 sind, wäre das Ergebnis der (idealen) sphärischen Interpolation der Punkt P1 an dem sich die Winkelhalbierende (orange) mit der Kreislinie schneidet.
Je stärker sich die Rotationen zweier Joints unterscheiden, desto größer wird also der Fehler (= Abstand zwischen v' und P1) des linearen Vertex Blending. Dies wird besonders deutlich, wenn z.B. ein menschlicher Charakter seine Hand oder seinen Arm dreht, die dann wie abgeschnürt aussieht.
Quaternion + Translationsvektor
In Quaternionen kann man Rotationen speichern und im Gegensatz zu Matrizen lassen sie sich auch sehr gut Interpolieren. Da ihnen aber die Translationsfähigkeit fehlt, benötigt man zusätzlich einen Vektor dafür. Wir möchten erreichen, dass sich ein Vertex wie folgt transformieren lässt:
mixedQuaternion = Quaternion[JointID[0]] * JointWeight[0]
+ Quaternion[JointID[1]] * JointWeight[1]
+ Quaternion[JointID[2]] * JointWeight[2]
+ Quaternion[JointID[3]] * JointWeight[3];
finalQuaternion = normalize(mixedQuaternion);
finalTranslation = Translation[JointID[0]] * JointWeight[0]
+ Translation[JointID[1]] * JointWeight[1]
+ Translation[JointID[2]] * JointWeight[2]
+ Translation[JointID[3]] * JointWeight[3];
finalPos = finalQuaternion * VPos + finalTranslation;
Dies ist möglich, aber ein kleines bisschen komplizierter, da wir eigentlich zwei Translationen haben: Eine vor und eine nach der Rotation. Diese müssen wir nun zusammenfassen zu nur einer Translation, die nach der Rotation stattfindet. Dazu wenden wir auf den ersten Translationsvektor einfach die Rotation des Joints an, bevor wir die Summe mit seinem "Kollegen" bilden:
Translation = Quaternion * (-TPoseJoint.AbsPos) + Joint.AbsPos;
Der große Vorteil der Quaternionen gegenüber den voherigen Ansätzen ist wie gesagt die gute Interpolierbarkeit. Wenn man die Quaternionen wie oben gewichtet addiert und das Resultat normalisiert, landet man immer auf der Kreislinie. Zwar entspricht dies nicht ganz der sphärischen Interpolation, aber es gibt einen mathematischen Beweis, der zeigt, dass man nie weiter als 8,15° (Winkel zwischen den beiden orangenen Linien) vom idealen Ergebnis entfernt ist. Dies ist eine obere Grenze für den Fehler - in der Praxis liegt man meistens noch deutlich darunter.
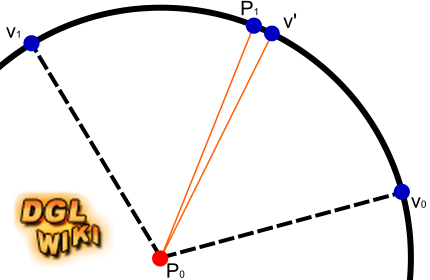
Dual Quaternions
Beim Dual Quaternion-Ansatz geht man im Prinzip den gleichen Weg, wie bei Matrizen. Man erzeugt also zwei Dual Quaternions für Translation und eines für Rotation. Via Multiplikation fasst man alle drei Transformationen in einem Dual Quaternion zusammen. Auf diese Weise erzeugt man für jeden Joint ein Dual Quaternion. Das Tolle an Dual Quaternions ist jedoch, dass man sie im Gegensatz zu Matrizen ganz hervorragend (genau wie gewöhnliche Quaternionen) interpolieren kann. Die Vertex-Transformation sieht also so aus:
finalDQ = DualQuat[JointID[0]] * JointWeight[0]
+ DualQuat[JointID[1]] * JointWeight[1]
+ DualQuat[JointID[2]] * JointWeight[2]
+ DualQuat[JointID[3]] * JointWeight[3];
finalDQ.normalize();
finalPos = finalDQ * VPos;
Was genau die letzten beiden Zeilen machen, ist im Artikel Dual Quaternion erklärt. Da Normalenvektoren der Translationsteil des Dual Quaternions nicht betrifft, wird auf ihn nur das nicht-duale Quaternion angewandt:
finalNormal = finalDQ.real * Normal
Dual Quaternion-Skinning bietet neben der schönen Interpolation den Vorteil, dass ein Dual Quaternion nur halb so viel Platz benötigt wie eine Matrix. Leider ist es jedoch nicht so schnell wie der Vertex-Blending Ansatz und die Mathematik dahinter ist schwer in aller Tiefe verstehen.
Implementation im Vertexshader
Ein Model hat in der Regel mehrere tausend Vertices und da man in Videospielen meistens auch noch mehrere animierte Models gleichzeitig sieht, müssen schnell mal einige zehntausend Vertices pro Frame per skeletaler Animation transformiert werden. Selbst heutige CPUs stoßen da schonmal an Grenzen - vor allem, wenn sie auch noch andere Aufgaben erledigen soll. Die benötigte Rechenleistung lässt sich nur durch Parallelisierung bereitstellen. Und - Quizfrage: Welcher Prozessor im PC arbeitet extrem parallel? Na...?
Ja, richtig: Die GPU. Also nutzen wir doch deren Shader-Rechenwerke für die Transformation. Genauer gesagt, werden wir den Vertexshader dafür nutzen:
#version 330
const int g_JointsMax = 64;
uniform mat4 u_ModelViewProjectionMatrix;
uniform mat3 u_NormalMatrix;
uniform vec4 u_DualQuats[g_JointsMax*2];
in vec3 inPos;
in vec3 inNormal;
in vec2 inTexCoord;
in vec4 inJointWeight;
in uvec4 inJointID;
out vec3 vf_Normal;
out vec2 vf_TexCoord;
void NormalizeDualQuat(inout vec4 real, inout vec4 dual)
{
real = normalize(real);
dual -= real * dot(real, dual);
}
void GetDualQuat(out vec4 real, out vec4 dual)
{
real = u_DualQuats[inJointID[0]*2u] * inJointWeight[0]
+ u_DualQuats[inJointID[1]*2u] * inJointWeight[1]
+ u_DualQuats[inJointID[2]*2u] * inJointWeight[2]
+ u_DualQuats[inJointID[3]*2u] * inJointWeight[3];
dual = u_DualQuats[inJointID[0]*2u +1u] * inJointWeight[0]
+ u_DualQuats[inJointID[1]*2u +1u] * inJointWeight[1]
+ u_DualQuats[inJointID[2]*2u +1u] * inJointWeight[2]
+ u_DualQuats[inJointID[3]*2u +1u] * inJointWeight[3];
NormalizeDualQuat(real, dual);
}
vec3 TransformPosition(vec3 v, vec4 real, vec4 dual)
{
vec3 term1 = cross(real.xyz, cross(real.xyz, v) + real.w*v);
v += 2.0 * (term1 + real.w*dual.xyz - dual.w*real.xyz + cross(real.xyz, dual.xyz));
return v;
}
vec3 TransformNormal(vec3 n, vec4 quat)
{
n += 2.0 * cross(quat.xyz, cross(quat.xyz, n) + quat.w*n);
return n;
}
void main(void)
{
vec3 skinnedPos = inPos;
vec3 skinnedNormal = inNormal;
// dual quaternion skinning
if(inJointWeight[0] > 0.0)
{
vec4 real, dual;
GetDualQuat(real, dual);
skinnedPos = TransformPosition(inPos, real, dual);
skinnedNormal = TransformNormal(inNormal, real);
}
// usual transformation
vf_TexCoord = inTexCoord;
vf_Normal = normalize(u_NormalMatrix * skinnedNormal);
gl_Position = u_ModelViewProjectionMatrix * vec4(skinnedPos, 1.0);
}
Dieser Vertexshader implementiert DualQuaternion-Skinning. Bei Vertices, die nicht geskinnt werden sollen, setzt man einfach die erste Komponente des Vertexattributs inJointWeight auf 0. Wie man sieht, ist die Implementierung sehr nahe am Pseudocode der Beschreibung des Ansatzes oben. Es sollte daher leicht fallen, auch die anderen Verfahren im Vertexshader zu implementieren.
Die Transformation mittels Quaternion und Translationsvektor würde z.B. so aussehen:
vec3 TransformPosition(vec3 v, vec4 quat, vec3 trans)
{
return TransformNormal(v, quat) + trans;
}
Schlusswort
Das war es auch schon mit meinem ersten Wiki-Artikel in der Kategorie Tutorial. Ich hoffe, die Erklärungen waren verständlich und nicht zu trocken. Falls nicht, gibt es immer noch unser Forum, das auf Feedback und Fragen wartet.
Natürlich kann man die in diesem Tutorial beschriebene Animationstechnik noch erweitern. Sinnvoll wäre z.B., wenn ein Charakter mehrere Animationen gleichzeitig ausführen kann (manche Animationen betreffen ja nur Teile des Skeletts) oder ein sanftes Überblenden vom Kriechen zum Gehen und vom Gehen zum Rennen.
Für diejenigen, die noch tiefer in die Materie der Charakteranimation einsteigen wollen, gibt es noch eine Menge anderer interessanter Techniken zu erlernen. Mittels inverser Kinematik kann man beispielsweise berechnen, wie sich der Rest des Skeletts bewegen muss, um einen bestimmten Joint eines Charakters an eine bestimmte Position zu bekommen. Damit lassen sich u.a. automatisch an die Umgebung angepasste Animationen erzeugen. Wenn du eine coole Technik erlernt hast, zu der es noch kein Tutorial auf DGL gibt, würde es (nicht nur) mich natürlich freuen, wenn du die Plattform nutzt, dein Wissen zu teilen. In diesem Sinne: Frohes Schaffen!