Tutorial Charakteranimation: Unterschied zwischen den Versionen
(Bild eingefügt) |
K (→Das Skelett: Hinweis zur Repräsentation von Knochen hinzugefügt) |
||
| Zeile 14: | Zeile 14: | ||
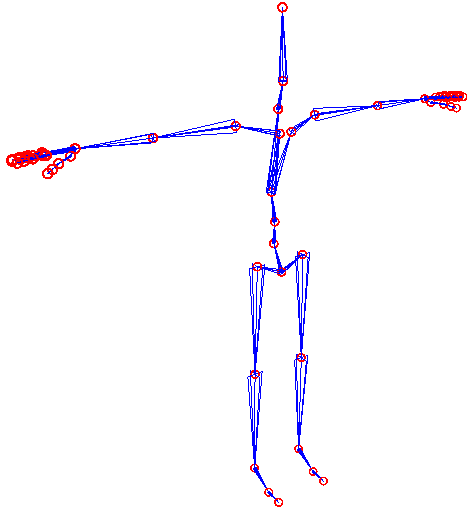
[[Bild:Skelett_T-Pose.png]] | [[Bild:Skelett_T-Pose.png]] | ||
| − | Mathematisch gesehen können wir ein Gelenk durch eine Rotation, eine Position, um die rotiert wird, und die Menge aller Untergelenke beschreiben. Die Rotation lässt sich auf viele Arten beschreiben, z.B. durch eine 3x3-[[Matrix]] oder ein [[Quaternion]]. Die Position beschreibt man am einfachsten durch einen Translationsvektor relativ zum Elternknoten. Die Rotation wird in der Regel auch erstmal relativ zum Elternknoten angegeben. Die absolute Rotation eines Gelenks erhält man ganz einfach, indem man die absolute Rotation des Elternknotens mit der eigenen relativen multipliziert: | + | Mathematisch gesehen können wir ein Gelenk durch eine Rotation, eine Position, um die rotiert wird, und die Menge aller Untergelenke beschreiben. Dadurch werden gleichzeitig auch alle Knochen beschrieben, da diese nichts weiter als die Verbindung zwischen einem Eltern- und Kind-Joint sind. Die Rotation lässt sich auf viele Arten beschreiben, z.B. durch eine 3x3-[[Matrix]] oder ein [[Quaternion]]. Die Position beschreibt man am einfachsten durch einen Translationsvektor relativ zum Elternknoten. Die Rotation wird in der Regel auch erstmal relativ zum Elternknoten angegeben. Die absolute Rotation eines Gelenks erhält man ganz einfach, indem man die absolute Rotation des Elternknotens mit der eigenen relativen multipliziert: |
<br>[Code]<br> | <br>[Code]<br> | ||
Die absolute Rotation des Elternknotens muss man natürlich vorher erst einmal berechnen (es sei denn, der Elternknoten ist die Wurzel). Ihr seht schon: Das ist ein rekursiver Vorgang. | Die absolute Rotation des Elternknotens muss man natürlich vorher erst einmal berechnen (es sei denn, der Elternknoten ist die Wurzel). Ihr seht schon: Das ist ein rekursiver Vorgang. | ||
Version vom 31. Dezember 2013, 23:23 Uhr
Bitte haben Sie etwas Geduld und nehmen Sie keine Änderungen vor, bis der Artikel hochgeladen wurde. |
| |
Dieses Tutorial befindet sich mitten in der Erstellung. Wie bist du überhaupt hierher gekommen? ;-) |
Inhaltsverzeichnis
Einleitung
In diesem Tutorial möchte ich euch beibringen, wie man starre Meshes lebendig erscheinen lässt, indem man sie bewegt. Und zwar wollen wir sie nicht nur verschieben und drehen, sondern richtig animieren, also verformen. Ein sicherer Umgang mit Matrizen, VBOs und Shadern wird hier vorausgesetzt.
Das Skelett
Es gibt verschiedene Ansätze, ein Mesh durch Animation zu verformen. Meistens möchte man in Computerspielen Menschen oder Tiere (oder etwas, das ihnen ähnelt) animieren, die sich nur sehr eingeschränkt verformen können - nämlich so, wie es ihr Skelett zulässt. Daher kommt meistens Skelett-basierte Animation zum Einsatz. Sich bewegene Maschinen oder Roboter sind meistens noch beschränkter in ihrer Bewegegungsfreiheit, sodass sich deren Animationen ebenfalls mittels eines Skeletts realisieren lässt. Die Idee ist einfach: Man speichert für einen Charakter nur, wie sich das Skelett bei einer Animation bewegt. Das Skelett besteht aus deutlich weniger Teilen, als das Mesh (die Haut) Vertices hat. Die Auswirkungen auf die Vertices selbst werden erst während des Renderns in Echtzeit berechnet. Durch dieses Verfahren wird eine Menge Speicherplatz, aber auch Aufwand beim Erstellen und Bearbeiten von Animationen gespart.
Woraus besteht also ein Skelett? Aus Gelenken (Joints) und Knochen (Bones). In der Grafikprogrammierung hat es sich bewährt, Skelette hierarchisch aufzubauen. Das heißt, es gibt genau ein Supergelenk, das keinem anderen Gelenk untergeordnet ist. Dieses Gelenk wird auch Wurzel genannt, denn in der Informatik würde man sagen, das Skelett ist ein Baum. Das Wurzelgelenk besitzt untergeordnete Gelenke (Kinder), die mit jeweils einem Knochen mit ihm verbunden sind. Dreht man nun das Wurzelgelenk, so drehen sich alle untergeordneten Knochen und Gelenke (und deren Kinder) mit. Dies entspricht der Realität: Wenn du deinen Arm hebst, d.h. dein Schultergelenk drehst, bewegen sich das Ellenbogen- und Handgelenk, sowie alle Knochen der Hand entsprechend mit.
Mathematisch gesehen können wir ein Gelenk durch eine Rotation, eine Position, um die rotiert wird, und die Menge aller Untergelenke beschreiben. Dadurch werden gleichzeitig auch alle Knochen beschrieben, da diese nichts weiter als die Verbindung zwischen einem Eltern- und Kind-Joint sind. Die Rotation lässt sich auf viele Arten beschreiben, z.B. durch eine 3x3-Matrix oder ein Quaternion. Die Position beschreibt man am einfachsten durch einen Translationsvektor relativ zum Elternknoten. Die Rotation wird in der Regel auch erstmal relativ zum Elternknoten angegeben. Die absolute Rotation eines Gelenks erhält man ganz einfach, indem man die absolute Rotation des Elternknotens mit der eigenen relativen multipliziert:
[Code]
Die absolute Rotation des Elternknotens muss man natürlich vorher erst einmal berechnen (es sei denn, der Elternknoten ist die Wurzel). Ihr seht schon: Das ist ein rekursiver Vorgang.
Die absolute Position lässt sich ebenfalls rekursiv berechnen. Man multipliziert die absolute Rotationsmatrix des Elternknotens mit der relativen Position und addiert anschließend die absolute Position des Elternknotens:
[Code]
Die Animation
Die Animation besteht nun aus einer Folge von KeyFrames. Ein KeyFrame beschreibt den Zustand des Skeletts zu einer bestimmten Zeit. Für jeden KeyFrame werden also gespeichert:
- Die Zeit
- Die Rotation jedes Joints (relativ zum Eltern-Joint)
- Die Position jedes Joints (ebenfalls relativ zum Eltern-Joint)
Die KeyFrames werden nach der Zeit sortiert in einem Array gespeichert. Zwischen den KeyFrames kann man interpolieren und somit auch Zustände des Skeletts zwischen zwei KeyFrames berechnen. Das macht man sich bei der Animation zu nutze.
Man benötigt also eine Zeitvariable time (vom Typ float), die man beim Starten der Animation auf 0 setzt. In jedem Frame (hier ist nicht KeyFrame gemeint, sondern Frame wie in Framerate) erhöht man time um die im letzten Frame vergangene Zeit. Nun sucht man den KeyFrame mit der größten Zeit, die noch kleiner ist als time. Bei der Suche sollte man ausnutzen, dass man die KeyFrames nach der Zeit sortiert hat. Es wäre unnötig langsam, jeden einzelnen KeyFrame der Liste abzuklappern. Besser wäre
- sich das Suchergebnis vom letzten Frame zu merken und die Suche ab dort zu starten oder
- eine binäre Suche oder
- eine proportionale Suche.
Die Suche liefert uns den Index k des gesuchten KeyFrames, so dass gilt:
KeyFrames[k].time < time <= KeyFrames[k+1].time
f = (time - KeyFrames[k].time) / (KeyFrames[k+1].time - KeyFrames[k].time)
Skinning
Schön und gut, wir wissen jetzt, was ein Skelett ist und wie man es dreht. Doch was ändert das am Mesh? Schließlich wollen wir in der Endanwendung ja nichts mehr vom Skelett sehen. Offensichtlich benötigen wir eine Möglichkeit, die Vertices des Meshs mit dem Skelett zu verbinden. Das ist nicht schwierig: Wir ordnen jedem Vertex die Nummer (einen Integer) des Gelenks zu, das ihn beeinflusst. Moment mal: Das Gelenk? Nur eines? Nein, eins allein reicht nicht aus. Denn was soll man beispielsweise mit einem Vertex machen, der auf der Haut des Handgelenks eines Menschen liegt? Gehört er zum Hand- oder doch zum Unterarmknochen? Die Antwort lautet: beides. Seine Position wird sowohl von der Drehung des Ellenbogens, als auch von der Drehung des Handgelenks beeinflusst. Das heißt, wir müssen jedem Vertex mindestens zwei Gelenke zuordnen. In der Praxis nimmt man oft sogar vier. So werden wir auch in diesem Tutorial verfahren.
Doch nun, da wir festgestellt haben, dass oft kein Knochen alleinigen Einfluss auf einen Vertex hat, müssen wir den Anteil an Einfluss auch noch speichern. Dafür hat sich der Begriff BoneWeight eingebürgert. Das BoneWeight hat einen Wert zwischen 0 und 1 und i.d.R. ist es so, dass die Summe aller BoneWeights eines Vertex 1 ergibt. Somit kann man ein wenig Speicherplatz sparen, da man das letzte BoneWeight jederzeit berechnen kann:
Leztes BoneWeight = 1 - (Summe aller anderen BoneWeights)
Verformung
Nun, da wir jedem Vertex eine Liste von Joints und deren Gewichte zugeordnet haben, können wir endlich ausrechnen, wie genau sich die Position durch die Joints ändert. Dazu gibt es verschiedene Ansätze, die jeweils ihre eigenen Vor- und Nachteile haben und sich vor allem in der Art der Interpolation zwischen mehreren Joints unterscheiden. Rotationsmatrix + Positionsvektor Dies ist der intuitivste Ansatz, da er sich praktisch direkt aus der oben stehenden Definition des Skeletts ergibt. Man nimmt sich die Position des Vertexes, den man transformieren möchte. Diese nennen wir im Folgenden VPos. Diesen Vektor möchten wir nun um das erste Gelenk rotieren. Dazu ziehen wir die absolute Position (JAbsPos) des Gelenks ab, multiplizieren das Ergebnis mit der Rotationsmatrix (JRotMatrix) des Gelenks und addieren anschließend die zuvor abgezogene absolute Gelenk-Position wieder drauf: [Code]res[0] = JRotMatrix[0] * (VPos - JAbsPos[0]) + JAbsPos[0];[/Code] Das wäre alles, wenn nur ein einziger Joint den Vertex beeinflussen würde. Da wir jedoch mehrere Joints pro Vertex haben, müssen wir diese Berechnung für jeden von ihnen wiederholen. Am Ende haben wir vier Vektoren res, die noch - unter Berücksichtigung des BoneWeights - gemittelt werden wollen: [Code]res[0] = res[0]*boneWeight[0] + res[1]*boneWeight[1] + res[2]*boneWeight[2] + res[3]*boneWeight[3];[/Code] So einfach geht das. Allerdings hat diese billige Methode einen ganz gravierenden Nachteil. [Bild] Dadurch, dass nicht die Rotationen selbst, sondern erst die fertig berechneten Positionen (linear) interpoliert werden, ergeben sich visuelle Artefakte in Form seltsamer Knicks. Das führt bei Menschen z.B. dazu, dass der Arm bei bestimmten Drehungen "abgeschnürt" wird. Man könnte nun auf die Idee kommen, diese 2 Translationen und die eine Rotation in eine 4x4-Matrix zu stecken, und dann die Matrizen zu interpolieren, statt die resultierenden Vektoren. Das bringt allerdings keine Besserung. Quaternion + Positionsvektor Dual Quaternions Dual Quaternions sind die mathematisch anspruchsvollste Methode, das Interpolationsproblem zu lösen. Dafür ist das Ergebnis qualitativ am höchsten und noch dazu sehr schnell und speicherplatzsparend - kurz: State-of-the-art.
ToDo
Bilder
Codes
Erst nur ein Joint/Vertex, dann erst mit Interpolation kommen
JointWeight vs. BoneWeight
Vertexshader