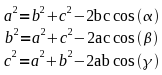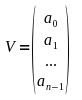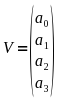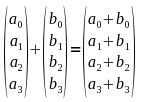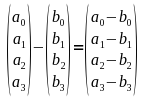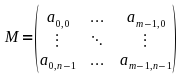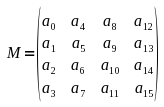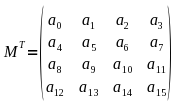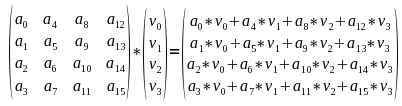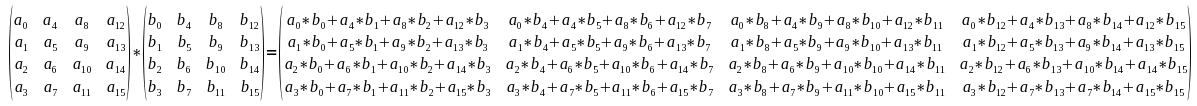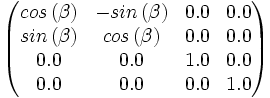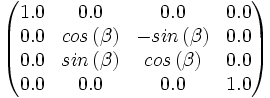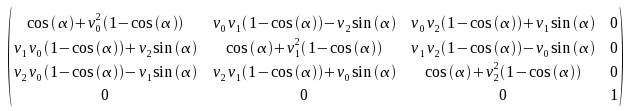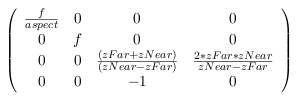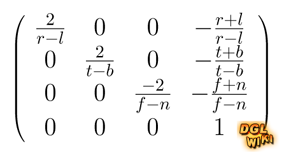Tutorial OpenGL3 Lineare Algebra: Unterschied zwischen den Versionen
Flash (Diskussion | Beiträge) K (→Sinus- und Kosinussatz) |
(→Vektor: Inhaltliche sowie grammatische Korrekturen) |
||
| (7 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | {{Unvollständig|Quaternion,Rechtschreibung und Grammatik sowie ein Inhaltscheck fehlen. Die einzelnen Matrizen müssen noch besser erklärt werden.}} | ||
=Vorwort= | =Vorwort= | ||
Lineare Algebra ist ein Teilgebiet der Mathematik und beschäftigt sich mit Vektorräumen. | Lineare Algebra ist ein Teilgebiet der Mathematik und beschäftigt sich mit Vektorräumen. | ||
| − | Die für OpenGL wichtigen Unterbereiche sind Vektoren und Matrizen. | + | Die für [[OpenGL]] wichtigen Unterbereiche sind Vektoren und Matrizen. |
| − | Der größte Teil der 3D Programmierung beschäftigt sich mit | + | Der größte Teil der 3D-Programmierung beschäftigt sich mit linearer Algebra, daher sollte auch dieser Grundlage eine besondere Aufmerksamkeit gewidmet werden. |
| − | Sollte der Inhalt | + | Sollte der Inhalt vielleicht zu viel für einmal sein, dann wäre es ratsam, ihn in mehreren Etappen zu bewältigen, aber es sollte auf jedenfall vollständig verstanden werden, bevor man sich ernsthaft mit OpenGL auseinandersetzen will. |
| + | |||
=Trigonometrie= | =Trigonometrie= | ||
| − | Da später in der Linearen Algebra auf die Trigonometrie | + | Da später in der Linearen Algebra auf die Trigonometrie zurückgegriffen wird, sollen als erstes die notwendigen Grundlagen in diesem Bereich beleuchtet werden. |
| + | |||
==Bogenmaß und Gradmaß== | ==Bogenmaß und Gradmaß== | ||
Man unterscheidet bei der Darstellung eines Winkels zwischen Bogenmaß(rad) und Gradmaß(deg). | Man unterscheidet bei der Darstellung eines Winkels zwischen Bogenmaß(rad) und Gradmaß(deg). | ||
Das Bogenmaß wird durch die Konstante Pi beschrieben, wobei der Wertebereich von 0 bis 2*Pi geht. | Das Bogenmaß wird durch die Konstante Pi beschrieben, wobei der Wertebereich von 0 bis 2*Pi geht. | ||
Das Gradmaß ist eine Einteilung, welche von 0 bis 360° abgebildet wird. | Das Gradmaß ist eine Einteilung, welche von 0 bis 360° abgebildet wird. | ||
| − | 0° sind 0, 90° sind 0.5*Pi, 180° sind Pi, 270° sind 2 | + | 0° sind 0, 90° sind 0.5*Pi, 180° sind Pi, 270° sind 3/2*Pi und 360° sind 2*Pi oder auch 0° und 0. |
| − | Um vom Bogenmaß | + | Um vom Bogenmaß ins Gradmaß umzurechnen, kann man folgende Formel verwenden: |
[[Datei:Tutorial_Lineare_Algebra_rad2deg.png]] | [[Datei:Tutorial_Lineare_Algebra_rad2deg.png]] | ||
| − | Für die Umwandlung | + | Für die Umwandlung vom Bogenmaß ins Gradmaß gilt diese Formel: |
[[Datei:Tutorial_Lineare_Algebra_deg2rad.png]] | [[Datei:Tutorial_Lineare_Algebra_deg2rad.png]] | ||
==Trigonometrische Funktionen== | ==Trigonometrische Funktionen== | ||
| − | Für das sinnvolle | + | Für das sinnvolle Arbeiten mit Winkelfunktionen benötigen wir einen Einheitskreis. |
| − | + | Dies ist ein Kreis, dessen Radius 1 ist und somit eine Reihe von Funktionen zulässt. | |
[[Datei:einheitsvektor.png]] | [[Datei:einheitsvektor.png]] | ||
| − | Der Einheitskreis ist wie folgt | + | Der Einheitskreis ist wie folgt beschriftet. In Blau sind die Bogenmaß Werte angegeben, in dunkelgrün die äquivalenten Werte der Kosinusfunktion und Orange ist der Winkel. Wenn man den Kosinus und Sinus von dem Winkel errechnet, dann erhält man den hellgrünen x- und roten y-Wert. Egal welchen Winkel man in der Sinus- und Kosinusfunktion einsetzt, der Wert wird nie größer 1 oder kleiner -1 werden. Aber halt, wieso? |
| + | |||
==Trigonometrie im allgemeinen Dreieck== | ==Trigonometrie im allgemeinen Dreieck== | ||
Man unterscheidet in der Trigonometrie zwischen rechtwinkligen Dreiecken und allgemeinen Dreiecken. | Man unterscheidet in der Trigonometrie zwischen rechtwinkligen Dreiecken und allgemeinen Dreiecken. | ||
| Zeile 37: | Zeile 41: | ||
[[Datei:sinussatz.png]] | [[Datei:sinussatz.png]] | ||
| − | Durch das Umstellen der Gleichungen kann man die einzelnen Winkel oder Seiten | + | Durch das Umstellen der Gleichungen kann man die einzelnen Winkel oder Seiten eines Dreiecks erhalten. Hierzu werden entweder zwei Seiten und ein Winkel oder zwei Winkel und eine Seite benötigt. |
Der Kosinussatz | Der Kosinussatz | ||
| Zeile 43: | Zeile 47: | ||
[[Datei:kosinussatz.png]] | [[Datei:kosinussatz.png]] | ||
| − | ermöglicht es, entweder aus drei gegebenen Seiten die Winkel auszurechnen oder aus zwei Seiten und ihrem Zwischenwinkel die | + | ermöglicht es, entweder aus drei gegebenen Seiten die Winkel auszurechnen oder aus zwei Seiten und ihrem Zwischenwinkel die gegenüberliegende Seite zu berechnen. |
===Eigenschaften und Formeln=== | ===Eigenschaften und Formeln=== | ||
| − | Es kann hilfreich sein, eine | + | Es kann hilfreich sein, eine Sinusfunktion in eine Kosinusfunktion umzuwandeln oder umgekehrt. Hierzu benötigt man die Komplementärformeln, welche wie folgt aussehen: |
[[Datei:costosin_sintocos.png]] | [[Datei:costosin_sintocos.png]] | ||
| − | Um den Rückgabewert | + | Um den Rückgabewert der Sinus- oder Kosinusfunktion in den Bogenmaß umzuwandeln, gibt es folgende Umkehrfunktionen. |
[[Datei:umkehrfunktion_sin_cos_tan.png]] | [[Datei:umkehrfunktion_sin_cos_tan.png]] | ||
| − | Es ist zu beachten, dass diese | + | Es ist zu beachten, dass diese Werte im Bogenmaß zurückgeben und diese für das Gradmaß entsprechend umgerechnet werden müssen. |
| + | |||
| + | Außerdem sollte man wissen, dass Sinus und Kosinus keine injektiven Funktionen sind. Das heißt auf deutsch: Wer arccos(cos(a)) berechnet, kann nicht sicher sein, dass das Ergebnis wieder a ist. Um dies nachzuvollziehen, setze man für a z.B. 3/2*pi ein (also 270°). Der Kosinus dieses Winkels ist 0 (siehe Zeichnung oben). Die Funktion arccos bekommt also das Argument 0 übergeben und soll den zugehörigen Winkel ausspucken. Das Problem ist: Es gibt nicht "den" zugehörigen Winkel, sondern zwei (und wenn man Winkel >360° oder <0 zulässt, sind es sogar unendlich viele). Die Arcus-Funktionen geben in diesem Fall den kleinsten Winkel >= 0 aus - also in diesem Fall pi/2 = 90° (siehe Zeichnung oben). | ||
=Vektor= | =Vektor= | ||
| − | Ein Vektor kann mit einem Array oder einer Liste | + | Ein Vektor kann mit einem Array oder einer Liste verglichen werden, wenn man z.B. einen 3-dimensionalen Vektor meint, dann wäre es ein Array mit 3 Elementen. |
Die übliche Schreibweise eines Vektors sieht wie folgt aus. | Die übliche Schreibweise eines Vektors sieht wie folgt aus. | ||
[[Datei:generischer_vektor.png]] | [[Datei:generischer_vektor.png]] | ||
| − | Eine entsprechende C++ | + | Eine entsprechende Representation in C++ wäre z.B. folgende: |
<source lang="cpp">class TVector4Float | <source lang="cpp">class TVector4Float | ||
{ | { | ||
| Zeile 69: | Zeile 75: | ||
};</source> | };</source> | ||
| − | OpenGL verwendet auf der Grafikkarte immer 4-dimensionale Vektoren, auch wenn nur 1 oder 3 benötigt werden. Die restlichen Elemente des Vektors werden dann mit 0 aufgefüllt. Vektoren werden in OpenGL in | + | OpenGL verwendet auf der Grafikkarte immer 4-dimensionale Vektoren, auch wenn nur 1 oder 3 Elemente benötigt werden. Die restlichen Elemente des Vektors werden dann mit 0 aufgefüllt. Vektoren werden in OpenGL in zwei Arten verwendet, als absoluter und als relativer Wert. Absolute Werte wären z.B. Positionen und Farbwerte, während relative Werte z.B. eine Transformation wäre. Der OpenGL-Vektor sieht wie folgt aus. |
[[Datei:opengl_vektor.png]] | [[Datei:opengl_vektor.png]] | ||
==Einheitsvektor== | ==Einheitsvektor== | ||
| − | + | Eine besondere Form eines Vektors ist der Einheitsvektor, welcher immer eine Länge von 1 hat. Davon gibt es unendlich viele, nämlich in jede Richtung einen. Wie man aus einem beliebigen Vektor (außer dem Nullvektor) einen Einheitsvektor macht, wird im Abschnitt Normalisierung erläutert. Einheitsvektoren sind als Normalen oder Richtungsvektoren in OpenGL im Einsatz und bilden die Basis für Rotationen. | |
| − | |||
| − | |||
==Addition== | ==Addition== | ||
| Zeile 83: | Zeile 87: | ||
[[Datei:addition_vektor1.png]] | [[Datei:addition_vektor1.png]] | ||
| − | Die Addition wird | + | Die Addition wird komponentenweise ausgeführt, was bedeutet, man kann sich eine Addition von Vektoren als eine Addition von jeden einzelnen Element mit dem entsprechenden Element im anderem Vektor vorstellen. |
[[Datei:addition_vektor_visual.png]] | [[Datei:addition_vektor_visual.png]] | ||
| − | Die Addition von Vektoren kann man sich sehr einfach | + | Die Addition von Vektoren kann man sich sehr einfach vorstellen, indem man die einzelnen Vektoren als Bewegungsbefehle sieht. Wenn man also 2 Schritte vorwärts, einen Schritt seitwärts laufen soll und danach ein halben Schritt vorwärts und ein Schritt seitwärts, dann kann man diese beiden Befehle auch zu einem Befehl zusammen fassen. Laufe 2 1/2 Schritte vorwärts und 2 Schritte seitwärts und wir stehen am gleichen Punkt und dieser Befehl wäre dann unser Ergebnis Vektor c. |
<source lang="cpp">class TVector4Float | <source lang="cpp">class TVector4Float | ||
| Zeile 106: | Zeile 110: | ||
[[Datei:subtraktion_vektor1.png]] | [[Datei:subtraktion_vektor1.png]] | ||
| − | Hier gilt gleiches | + | Hier gilt gleiches wie bei der Addition, nur dass komponentenweise subtrahiert wird. |
[[Datei:Subtraktion_vektor_visual.png]] | [[Datei:Subtraktion_vektor_visual.png]] | ||
| − | Bei der Subtraktion eines Vektors wendet man den ersten Befehl an und läuft z.B. 2 Schritte nach vorne und einen | + | Bei der Subtraktion eines Vektors wendet man den ersten Befehl an und läuft z.B. 2 Schritte nach vorne und einen seitwärts, dann wendet man den 2. Schritt an aber wechselt das Vorzeichen jeder einzelnen Komponente. Also wird eine positive Komponente zu einer negativen und eine negative zu einer positiven. Wenn man also einen Schritt seitwärts, nach links, laufen soll, dann läuft man einen Schritt seitwärts, nach rechts, sowie vorwärts statt rückwärts. Man kann eine Subtraktion über eine Addition realisieren, wenn man jede Subtraktion, den rechten Vektor zuvor invertiert und dann addiert. |
<source lang="cpp">class TVector4Float | <source lang="cpp">class TVector4Float | ||
{ | { | ||
| Zeile 127: | Zeile 131: | ||
[[Datei:magnitude_vektor.png]] | [[Datei:magnitude_vektor.png]] | ||
| − | Magnitude ist der | + | Magnitude ist der englische Begriff für die Berechnung des Betrags oder auch der Länge eines Vektors. |
| − | Die Länge des Vektors wird benötigt, wenn man einen Vektor | + | Die Länge des Vektors wird benötigt, wenn man einen Vektor normalisieren will oder feststellen möchte, ob ein Vektor ein Einheitsvektor ist. |
[[Datei:betrag_vektor.png]] | [[Datei:betrag_vektor.png]] | ||
| − | Der Betrag eines Vektors kann über den Satz des | + | Der Betrag eines Vektors kann über den Satz des Pythagoras ermittelt werden, welcher die Wurzel der Summe der Quadrate aller Komponenten ist. |
| − | Dies ist natürlich für wenige gut | + | Dies ist natürlich für wenige gut vorstellbar und daher hier mal eine bessere Erklärung. Ein Vektor kann in n Komponenten zerlegt werden, der 4 Komponenten Vektor von OpenGL in 4 Komponenten. Jede Komponente stellt eine Dimension dar, welche x,y,z und w sind. Pythagoras lernt man in der Schule im zweidimensionalen Raum kennen, also wie es im Abbild über diesen Text dargestellt ist. Die Regel besagt, das der Flächeninhalt einer Seite der Summe der anderen entspricht, also l²=x²+y². |
| − | Diese Flächen sind | + | Diese Flächen sind quadratisch, also hat jede Seite der Fläche die gleiche Kantenlänge. Wenn man die Quadratwurzel von der Fläche zieht, bekommt man also die Kantenlänge. Wenn man nun die Flächen von x,y,z und w summiert erhält man die Fläche l². Zieht man von l² die Quadratwurzel, dann hat man die Kantenlänge l von dem 4Komponenten Vektor, welche als Betrag oder Länge bezeichnet wird. Da bei einem Vektor w=0.0 gesetzt wird, hat diese keinen Einfluss auf diese Operation und wird in den Formeln und auch in der Regel nicht mit hingeschrieben. |
<source lang="cpp">class TVector4Float | <source lang="cpp">class TVector4Float | ||
| Zeile 150: | Zeile 154: | ||
[[Datei:skalarprodukt_vektor.png]] | [[Datei:skalarprodukt_vektor.png]] | ||
| − | Das Skalarprodukt erlaubt uns die Berechnung | + | Das Skalarprodukt erlaubt uns die Berechnung des Winkels zwischen 2 Vektoren. Hierfür müssen allerdings beide Vektoren normalisiert sein, also jeweils einen Betrag von 1 haben. Andernfalls muss dies noch nachträglich getan werden. |
[[Datei:skalarprodukt_vektor1.png]] | [[Datei:skalarprodukt_vektor1.png]] | ||
| − | Wenn die | + | Wenn die zwei Vektoren a und b vorliegen, sollte man davon ausgehen, dass der Betrag beider Vektoren jeweils 1 ist. Sollte es nicht der Fall sein, so wie im Bild über diesen Text, dann muss dies durch die Normalisierung nachgeholt werden. Dies passiert, indem man für jeden Vektor den Betrag errechnet und dann den Vektor komponentenweise durch diesen Betrag dividiert. Die oben stehende Formel wird aus dem Kosinussatz abgeleitet und umgestellt. Daraus ergibt sich am Ende, dass die Summe der komponentenweise multiplizierten Vektoren a und b den Kosinus des Winkels ergibt. Es ist wichtig zu beachten, dass nicht der Winkel sondern der Kosinus des Winkels in c wieder zu finden ist. Wenn man den Winkel haben möchte, dann muss man den Arkuskosinus von c berechnen und das Ergebnis ggf. vom Bogenmaß ins Gradmaß umwandeln, um den Winkel (als Delta markiert) zu bekommen. |
<source lang="cpp">class TVector4Float | <source lang="cpp">class TVector4Float | ||
| Zeile 171: | Zeile 175: | ||
[[Datei:kreuzprodukt_vektor.png]] | [[Datei:kreuzprodukt_vektor.png]] | ||
| − | Das Kreuzprodukt errechnet einen Vektor, der senkrecht zu den Vektoren a und b steht, wenn a und b den selben Ursprung haben. Dieses Verhalten wird | + | Das Kreuzprodukt errechnet einen Vektor, der senkrecht zu den Vektoren a und b steht, wenn a und b den selben Ursprung haben. Dieses Verhalten wird genutzt, um die [[Normale]] einer Fläche zu errechnen. |
[[Datei:kreuzprodukt_vektor1.png]] | [[Datei:kreuzprodukt_vektor1.png]] | ||
| − | Der berechnete Vektor hat wie schon erwähnt die Eigenschaft, dass er senkrecht zu den Vektoren a und b ausgerichtet ist. Dies bedeutet, dass der Winkel zwischen dem | + | Der berechnete Vektor hat wie schon erwähnt die Eigenschaft, dass er senkrecht zu den Vektoren a und b ausgerichtet ist. Dies bedeutet, dass der Winkel zwischen dem berechnetem Vektor und a oder b immer 90° beträgt. Wenn a und b die Verbindungsvektoren von einem Eckpunkt eines Dreiecks zu den beiden anderen sind, dann zeigt der Vektor c senkrecht zum Dreieck und bildet den Richtungsvektor des Dreiecks. Wenn man nun noch diesen Vektor normalisiert, dann erhält man die Flächenormale. Diese hat den Betrag 1 und wird für verschiedene Rendertechniken, sowie Physikberechnungen benötigt. |
| − | Wenn z.B. ein Lichtstrahl solch ein Dreieck schneidet, dann kann man mit Hilfe des | + | Wenn z.B. ein Lichtstrahl solch ein Dreieck schneidet, dann kann man mit Hilfe des Richtungsvektors (vom Lichstrahl) und der Normale (der Fläche) den Reflektionsvektor berechnen und somit sagen, in welche Richtung sich das Licht weiter bewegen würde. |
| − | Es ist zu beachten, dass die Reihenfolge, in der man beide Vektoren | + | Es ist zu beachten, dass die Reihenfolge, in der man beide Vektoren multipliziert, einen Einfluss auf die Richtung, in die c zeigt, hat. |
Wenn man a und b tauscht, dann wechseln die Vorzeichen aller Komponenten von c. | Wenn man a und b tauscht, dann wechseln die Vorzeichen aller Komponenten von c. | ||
| Zeile 186: | Zeile 190: | ||
{ | { | ||
TVector4Float c; | TVector4Float c; | ||
| − | unsigned int | + | unsigned int next,nextnext; |
for (unsigned int i=0;i<4;i++) | for (unsigned int i=0;i<4;i++) | ||
{ | { | ||
| − | + | next = (i+1) % 4;//i+1 Modulo 4 | |
| − | + | nextnext = (i+2) % 4; | |
| − | + | c.m_Vec[i] = m_Vec[next]*b.m_Vec[nextnext] - m_Vec[nextnext]*b.m_Vec[next]; | |
| − | |||
| − | |||
| − | c.m_Vec[i]= | ||
} | } | ||
return c; | return c; | ||
| Zeile 200: | Zeile 201: | ||
};</source> | };</source> | ||
| − | == | + | ==Normalisierung== |
[[Datei:normalisieren_vektor.png]] | [[Datei:normalisieren_vektor.png]] | ||
| − | Bei der Normalisierung wird | + | Bei der Normalisierung wird ein Vektor durch seinen Betrag dividiert und man erhält einen Vektor, der in die gleiche Richtung zeigt, aber auf die Länge 1 skaliert ist. |
<source lang="cpp">class TVector4Float | <source lang="cpp">class TVector4Float | ||
| Zeile 210: | Zeile 211: | ||
TVector4Float Normalisieren(){ | TVector4Float Normalisieren(){ | ||
TVector4Float c; | TVector4Float c; | ||
| − | c=(*this)/this->Betrag(); | + | c = (*this)/this->Betrag(); |
return c; | return c; | ||
} | } | ||
| Zeile 227: | Zeile 228: | ||
{ | { | ||
protected: | protected: | ||
| − | TVector4Float m_Matrix[4]; //Erlaubt uns das | + | TVector4Float m_Matrix[4]; //Erlaubt uns das Nutzen von der eigenen Vektorklasse. |
float m_Array[16]; //für die LoadMatrix Funktion von OpenGL | float m_Array[16]; //für die LoadMatrix Funktion von OpenGL | ||
public: | public: | ||
| − | TVector4Float& Vektor(int Index)//Gibt eine Referenz vom Vektor zurück, was wie ein Pointer ist aber 100% auf ein Speicher zeigt, der existiert. | + | TVector4Float& Vektor(int Index)//Gibt eine Referenz vom Vektor zurück, was wie ein Pointer ist, aber 100% auf ein Speicher zeigt, der existiert. |
{ | { | ||
return m_Matrix[Index]; | return m_Matrix[Index]; | ||
| Zeile 237: | Zeile 238: | ||
T* GetMatrix1DArray()//Liefert den Pointer von der m_Array variable zurück. | T* GetMatrix1DArray()//Liefert den Pointer von der m_Array variable zurück. | ||
{ | { | ||
| − | //Überträgt die Daten von den einzelnen Vektoren in die OpenGL kompatible Matrix(m_Array). | + | //Überträgt die Daten von den einzelnen Vektoren in die OpenGL-kompatible Matrix(m_Array). |
for (int i=0;i<4;i++) | for (int i=0;i<4;i++) | ||
memcpy(&m_Array[i*4],&m_Matrix[i][0],16); | memcpy(&m_Array[i*4],&m_Matrix[i][0],16); | ||
| Zeile 244: | Zeile 245: | ||
};</source> | };</source> | ||
| − | Für Matrizen brauchen wir nicht so viele Funktionen wie bei Vektoren, um genau zu | + | Für Matrizen brauchen wir nicht so viele Funktionen wie bei Vektoren, um genau zu sein brauchen wir nur zwei Operationen. Diese Operationen sind das Transponieren und die Multiplikation. |
| − | Bei der Matrix benötigen wir einige Konstruktionsfunktionen und zwar Identity, Translate, Rotate und Scale Matrix. Diese Matrizen machen die ganze Arbeit für uns, wenn man sich in einem 3D Raum bewegen möchte, welcher als Modelview Matrix abgebildet wird. | + | Bei der Matrix benötigen wir einige Konstruktionsfunktionen und zwar Identity, Translate, Rotate und Scale Matrix. Diese Matrizen machen die ganze Arbeit für uns, wenn man sich in einem 3D-Raum bewegen möchte, welcher als Modelview Matrix abgebildet wird. |
==Transponieren== | ==Transponieren== | ||
[[Datei:transponieren_matrix.png]] | [[Datei:transponieren_matrix.png]] | ||
| − | Transponieren wird durch ein großes T über der Matrix dargestellt. Diese Funktion tauscht die Werte einer Matrix miteinander aus, so das aus einer Spalten konstruierten Matrix eine | + | Transponieren wird durch ein großes T über der Matrix dargestellt. Diese Funktion tauscht die Werte einer Matrix miteinander aus, so das aus einer Spalten konstruierten Matrix eine zeilenweise konstruierte Matrix wird. Diese Funktion kann hilfreich sein, wenn man zwischen Direct3D und OpenGL Daten austauschen will, denn nicht jeder nutzt spaltenorientierte Matrizen. |
[[Datei:opengl_matrix.png]][[Datei:d3d_matrix.png]] | [[Datei:opengl_matrix.png]][[Datei:d3d_matrix.png]] | ||
| Zeile 272: | Zeile 273: | ||
==Multiplikation== | ==Multiplikation== | ||
Multiplikation ist die wichtigste Operation bei Matrizen, wenn wir uns mit OpenGL beschäftigen. | Multiplikation ist die wichtigste Operation bei Matrizen, wenn wir uns mit OpenGL beschäftigen. | ||
| − | Dies liegt daran, dass OpenGL | + | Dies liegt daran, dass OpenGL zwei verschiedene Matrizen verwendet, um Vektoren in Bildschirmkoordinaten umzuwandeln. Damit dies funktioniert muss jeder Vektor mit diesen Matrizen jeweils multipliziert werden. Um eine Matrix zu manipulieren, wird diese mit einer konstruierten Matrix multipliziert. Diese Operation die ist meistausgeführte Operation sowohl in der OpenGL-Pipeline als auch in einem Spiel. Seit OpenGL3 gibt es kein Matrizensupport mehr, was bedeutet, dass man diese selber implementieren muss und dann die fertigen Matrizen an OpenGL übergibt. Die lässt viel Raum für Optimierung und kann somit ein OpenGL3-Programm schneller machen als ein OpenGL2-Programm, wenn man zuvor die glTranslate,glRotate und weiteren Funktionen verwendet hat. Es ist also ratsam sich eine sehr performante Bibliothek zu laden oder mit einem Performance Analyzer bewaffnet den eigenen Code zu optimieren. |
| + | |||
===Multiplikation mit einem Vektor=== | ===Multiplikation mit einem Vektor=== | ||
[[Datei:multiplikation_matrix_vektor.png]] | [[Datei:multiplikation_matrix_vektor.png]] | ||
| Zeile 278: | Zeile 280: | ||
[[Datei:multiplikation_matrix_vektor1.png]] | [[Datei:multiplikation_matrix_vektor1.png]] | ||
| − | Um eine Matrix mit einem Vektor zu multiplizieren, braucht man man nur den Vektor[n] von der Matrix mit der Komponente[n] von dem Vektor multiplizieren und die resultierenden Vektoren anschließend addieren. Hierbei wird also ein Vektor mit einer einzelnen Komponente multipliziert, was weiter oben | + | Um eine Matrix mit einem Vektor zu multiplizieren, braucht man man nur den Vektor[n] von der Matrix mit der Komponente[n] von dem Vektor multiplizieren und die resultierenden Vektoren anschließend addieren. Hierbei wird also ein Vektor mit einer einzelnen Komponente multipliziert, was weiter oben bei den Vektoren erklärt wurde. |
<source lang="cpp">class TMatrix4x4Float | <source lang="cpp">class TMatrix4x4Float | ||
| Zeile 295: | Zeile 297: | ||
[[Datei:multiplikation_matrix1.png]] | [[Datei:multiplikation_matrix1.png]] | ||
| − | Es sieht recht aufwändig aus allerdings kann man es dank der vorigen Matrix-Vektor Multiplikation auf | + | Es sieht recht aufwändig aus, allerdings kann man es dank der vorigen Matrix-Vektor-Multiplikation auf ein recht übersichtliches Maß runterstreichen. Man braucht dann nur noch die Matrix a jeweils mit einem der Vektoren von Matrix b multiplizieren und hat die Matrix-Matrix-Multiplikation erledigt. |
<source lang="cpp">class TMatrix4x4Float | <source lang="cpp">class TMatrix4x4Float | ||
| Zeile 309: | Zeile 311: | ||
=Konstruieren von Matrizen= | =Konstruieren von Matrizen= | ||
| − | == | + | ==Einheitsmatrix== |
| − | Die | + | Die Einheitsmatrix (engl. ''identity matrix'') ist die Initialisierungsmatrix, mit der alle Matrizen belegt werden. |
| − | Diese ist recht einfach und hat denn Sinn, dass bei einer Multiplikation immer der Wert | + | Diese ist recht einfach und hat denn Sinn, dass bei einer Multiplikation immer der Wert herauskommt, mit dem diese multipliziert wurde. |
| − | Wer aufmerksam | + | Wer aufmerksam gelesen hat, der wird nun an Einheitsvektoren denken und liegt richtig. |
| − | Aufgrund der | + | Aufgrund der Beschaffenheit einer Matrix benötigen wir in jeder Reihe und Spalte jeweils ein Element, welches den Wert 1 annimmt und die restlichen nehmen den Wert 0 an. Die sieht dann wie folgt aus: |
[[Datei:Tutorial_Nachsitzen_IdentityMatrix.png]] | [[Datei:Tutorial_Nachsitzen_IdentityMatrix.png]] | ||
| − | + | ||
<source lang="cpp">class TMatrix4x4Float | <source lang="cpp">class TMatrix4x4Float | ||
{ | { | ||
//... | //... | ||
| − | static TVector4Float Identity[4];//Statische Variable, welche nur einmal existiert. | + | static const TVector4Float Identity[4];//Statische Variable, welche nur einmal existiert. |
void LadeIdentity() | void LadeIdentity() | ||
| Zeile 332: | Zeile 334: | ||
TVector4Float TMatrix4x4Float::Identity[4]={TVector4Float(1.0,0.0,0.0,0.0),TVector4Float(0.0,1.0,0.0,0.0),TVector4Float(0.0,0.0,1.0,0.0),TVector4Float(0.0,0.0,0.0,1.0)};</source> | TVector4Float TMatrix4x4Float::Identity[4]={TVector4Float(1.0,0.0,0.0,0.0),TVector4Float(0.0,1.0,0.0,0.0),TVector4Float(0.0,0.0,1.0,0.0),TVector4Float(0.0,0.0,0.0,1.0)};</source> | ||
| − | == | + | |
| − | Wenn man | + | ==Translation== |
| − | Dazu erstellt man eine Matrix, füllt sie mit der | + | Wenn man einen Vektor oder eine Matrix in x,y,z bewegen möchte, dann kann man dies mit einer Transformationsmatrix erreichen. |
| + | Dazu erstellt man eine Matrix, füllt sie mit der Einheitsmatrix und setzt dann x,y,z in der Matrix mit den zu x,y,z Werten, um die man etwas verschieben möchte. | ||
[[Datei:Tutorial_Nachsitzen_MoveMatrix.png]] | [[Datei:Tutorial_Nachsitzen_MoveMatrix.png]] | ||
| Zeile 350: | Zeile 353: | ||
} | } | ||
};</source> | };</source> | ||
| − | == | + | ==Rotation== |
| − | Das Bewegen auf den | + | Das Bewegen auf den drei Achsen ist allerdings oft nicht ausreichend und deswegen gibt es auch eine Rotationsmatrix. |
| − | Die | + | Die Rotationsmatrix wird durch drei Vektoren beschrieben, welche jeweils für die x-, y- und z-Achse zuständig sind. |
| − | Man kann die Rotation | + | Man kann die Rotation der einzelnen Achsen in einem Schritt erledigen oder in 3 einzelne aufteilen. Um die Rotationsmatrix besser zu verstehen, werden erst einmal alle Achsen einzeln betrachtet. |
===Drehen um die Z-Achse=== | ===Drehen um die Z-Achse=== | ||
| Zeile 359: | Zeile 362: | ||
[[Datei:Tutorial_Nachsitzen_rotz.gif]][[Datei:Tutorial_Nachsitzen_RotZMatrix.png]] | [[Datei:Tutorial_Nachsitzen_rotz.gif]][[Datei:Tutorial_Nachsitzen_RotZMatrix.png]] | ||
| − | Der Z-Achsen Einheitsvektor(3. Spalte=0.0, 0.0, 1.0, 0.0) bleibt bei der Rotation unverändert - man nehme einen Finger, deute damit nach vorne. Nun drehe man diesen Finger um seine eigene Achse, wohin zeigt er? In die selbe Richtung wie vor der Drehung? Damit entspricht Z-Achsen Einheitsvektor auch der vorletzen Spalte der Matrix: (0.0, 0.0, 1.0, 0.0) | + | Der Z-Achsen-Einheitsvektor(3. Spalte=0.0, 0.0, 1.0, 0.0) bleibt bei der Rotation unverändert - man nehme einen Finger, deute damit nach vorne. Nun drehe man diesen Finger um seine eigene Achse, wohin zeigt er? In die selbe Richtung wie vor der Drehung? Damit entspricht Z-Achsen-Einheitsvektor auch der vorletzen Spalte der Matrix: (0.0, 0.0, 1.0, 0.0) |
| − | Der X-Achsen Einheitsvektor(1. Spalte=1.0, 0.0, 0.0 0.0) dreht sich hingegen mit. Trigonometrie findet der Lösung Spur. Ein Blick auf das Bild zum Einheitskreis zeigt, dass wir gerade das gleiche Problem für X und Y zu bewältigen haben: Die Rotationsachse ist in beiden Fällen die Z-Achse. Der Einheitsvektor, der gedreht wird, ist der X-Achsen Einheitsvektor also: | + | Der X-Achsen-Einheitsvektor(1. Spalte=1.0, 0.0, 0.0 0.0) dreht sich hingegen mit. Trigonometrie findet der Lösung Spur. Ein Blick auf das Bild zum Einheitskreis zeigt, dass wir gerade das gleiche Problem für X und Y zu bewältigen haben: Die Rotationsachse ist in beiden Fällen die Z-Achse. Der Einheitsvektor, der gedreht wird, ist der X-Achsen-Einheitsvektor also: |
<source lang="cpp">x = cos(ß) | <source lang="cpp">x = cos(ß) | ||
y = sin(ß)</source> | y = sin(ß)</source> | ||
womit der Inhalt der ersten Spalte der Matrix kennen: (cos(ß), sin(ß), 0.0, 0.0) | womit der Inhalt der ersten Spalte der Matrix kennen: (cos(ß), sin(ß), 0.0, 0.0) | ||
| − | Dies kann man auch auf den Y-Achsen Einheitsvektor(2. Spalte=0.0, 1.0, 0.0, 0.0) übertragen, man muss nur | + | Dies kann man auch auf den Y-Achsen-Einheitsvektor(2. Spalte=0.0, 1.0, 0.0, 0.0) übertragen, man muss nur beachten, in welcher Weise man dafür x und y vertauschen muss: |
<source lang="cpp">x = -sin(ß) | <source lang="cpp">x = -sin(ß) | ||
y = cos(ß)</source> | y = cos(ß)</source> | ||
| Zeile 377: | Zeile 380: | ||
[[Datei:Tutorial_Nachsitzen_roty.gif]][[Datei:Tutorial_Nachsitzen_RotYMatrix.png]] | [[Datei:Tutorial_Nachsitzen_roty.gif]][[Datei:Tutorial_Nachsitzen_RotYMatrix.png]] | ||
| − | Die Berechnung der Matrix wird auf die gleiche | + | Die Berechnung der Matrix wird auf die gleiche Weise ermittelt wie bei der Berechnung der Rotationsmatrix für die Drehung um die Z-Achse. |
===Drehen um die X-Achse=== | ===Drehen um die X-Achse=== | ||
| Zeile 385: | Zeile 388: | ||
===Rotation um alle Achsen mit einer Matrix=== | ===Rotation um alle Achsen mit einer Matrix=== | ||
| − | Es ist recht aufwändig für die CPU und für den Programmierer immer | + | Es ist recht aufwändig für die CPU und für den Programmierer, immer drei Rotationen auszuführen, deswegen hat man diese auch zu einer einzigen Operation zusammengefasst. Die Matrizen werden einfach miteinander multipliziert und es kommt eine Rotationsmatrix heraus, welche drei Eingabeparameter benötigt, alpha, beta und gamma sind dabei die Winkel für X-,Y- und Z-Achse. |
[[Bild:rotationsmatrix_3angle.png]] | [[Bild:rotationsmatrix_3angle.png]] | ||
| − | Eine weitere Möglichkeit, um eine Rotationsmatrix zu erstellen, wäre das | + | Eine weitere Möglichkeit, um eine Rotationsmatrix zu erstellen, wäre das Nutzen eines Richtungsvektors und eines Winkels. Hierbei wird der Winkel auf den Richtungsvektor angewendet, wenn man also als Vektor (1,0,0) verwendet, dann hat man eine Rotation auf der X-Achse, (0,1,0) Y-Achse und (0,0,1) für die Z-Achse. Man kann nun auch Vektoren wie (1,1,1) angeben, wobei die Funktion diesen Vektor dann normalisieren wird, damit er noch auf das Einheitskreis System funktioniert. Dieser Vektor ist nicht äquivalent mit dem Rotieren von X-,Y- und Z-Achse nacheinander. Der Vorteil hierbei liegt in der Kompaktheit des Codes und man kann auf Algorithmen zurückgreifen, die vor OpenGL3 entwickelt wurden, da der OpenGL-Treiber früher die Rotation über diese Variante implementiert hatte. |
[[Bild:rotationsmatrix.png]] | [[Bild:rotationsmatrix.png]] | ||
| Zeile 429: | Zeile 432: | ||
};</source> | };</source> | ||
| − | == | + | ==Skalieren== |
[[Bild:skalierungsmatrix.png]] | [[Bild:skalierungsmatrix.png]] | ||
| − | Die Skalierung ist eine sehr einfache Matrix, in der für die 1 | + | Die Skalierung ist eine sehr einfache Matrix, in der für die 1 des Einheitsvektors der entsprechende Skalierungsfaktor angegeben wird. Wenn man die Matrix mit einem Vektor multipliziert, dann werden X, Y und Z des Vektors mit den x- ,y- und z-Werten in der Skalierungsmatrix multipliziert und damit skaliert. Wenn man etwas größer machen will, dann wird der Wert entsprechend über 1.0 gewählt (z.B. 2.0 wäre doppelte Größe), und für eine Verkleinerung würde man ein Wert zwischen 1.0 und 0.0 wählen. Der Wert 0.5 würde z.B. eine Division durch 2 bedeuten, also 3*0.5=1.5. Der 4. Einheitsvektor wird so belassen, da wir diesen nur aus Kompatibilitätsgründen zu den 4-Komponenten-Vektoren benötigen. |
=Vom Vektor zur Bildschirmkoordinate= | =Vom Vektor zur Bildschirmkoordinate= | ||
Auf in den Endspurt! | Auf in den Endspurt! | ||
| − | Alle | + | Alle mathematischen Formeln und Funktionen benötigen wir, um die letzten zwei Punkte behandeln zu können. |
| − | Die Rede ist von der Umwandlung eines Vektors im 3D Raum in den 2D Raum, auf dem Bildschirm. | + | Die Rede ist von der Umwandlung eines Vektors im 3D-Raum in den 2D-Raum, auf dem Bildschirm. |
In Rahmen dieses Artikel wird nur auf die Transformation der Vektoren eingegangen und in einem späterem Artikel dann die weiteren Zwischenschritte zum Zeichnen einer Geometrie. | In Rahmen dieses Artikel wird nur auf die Transformation der Vektoren eingegangen und in einem späterem Artikel dann die weiteren Zwischenschritte zum Zeichnen einer Geometrie. | ||
| + | |||
==Modelview== | ==Modelview== | ||
[[Bild:weltkoordinatensystem-vs-modellkoordinatensystem.png]] | [[Bild:weltkoordinatensystem-vs-modellkoordinatensystem.png]] | ||
[[Bild:translation-vs-rotation.png]] | [[Bild:translation-vs-rotation.png]] | ||
| − | Die Modelview kann man sich wie ein 3D Unterraum vorstellen oder einer Transformation des Raumes. Die Modelview sorgt dafür, dass alle Vektoren, die mit dieser | + | Die Modelview kann man sich wie ein 3D-Unterraum vorstellen oder einer Transformation des Raumes. Die Modelview sorgt dafür, dass alle Vektoren, die mit dieser multipliziert werden, zu dieser Modelview ausgerichtet werden und die Modelview ist relativ zur Welt ausgerichtet. Dies bedeutet, wenn man für jedes Objekt eine Modelview erzeugt, dann kann dieses Objekt relativ zur Welt ausgerichtet werden, sobald man die Vektoren des Objektes mit der Modelview multipliziert. Wieso richtet man die Vektoren nicht gleich zur Welt aus, statt den Umweg über die Modelview Matrix zu gehen? Die Antwort ist schlicht "Optimierung". Es wäre zu langsam, wenn man jeden Renderdurchgang jedes einzelne Vertex im Speicher lesen müsste, die neue Position berechnen, im Speicher updaten und in der Pipeline weiter zu arbeiten. Es ist auch speichereffizienter, da z.B. gleiche Objekte nur einmal in den Speicher abgelegt werden müssen und nur zwei unterschiedliche Modelview-Matrizen benötigt werden. |
| − | Im rechten Bild kann man | + | Im rechten Bild kann man zwei aufeinanderfolgende Befehlsketten sehen, die Transformationen auf ein Objekt anwenden. Dieses Bild soll noch einmal verdeutlichen, dass das Anwenden von Befehlen auf eine Modelview-Matrix ''nicht'' kommutativ ist (a*b ist im Allgemeinen nicht das gleiche wie b*a). |
| − | Während vor OpenGL3 die Modelview Matrix von den OpenGL Treibern verwaltet wurde, muss dies ab OpenGL3 vom | + | Während vor OpenGL3 die Modelview-Matrix von den OpenGL-Treibern verwaltet wurde, muss dies ab OpenGL3 vom Nutzer gemacht werden und auch das Aktualisieren in der Renderpipeline muss nun vom Entwickler übernommen werden. Wie dies funktioniert, wird in einem späteren Artikel erklärt. Es ist nur noch wichtig zu sagen, dass die GPU diese Matrix mit jeden Vertex multipliziert, der durch die Renderpipeline geschickt wird. |
==Normal-Matrix== | ==Normal-Matrix== | ||
| − | Die Normal-Matrix wurde vor OpenGL3 als [[gl_NormalMatrix]] automatisch berechnet aber mit OpenGL3 ist auch diese aus dem Treiber entfernt worden. | + | Die Normal-Matrix wurde vor OpenGL3 als [[gl_NormalMatrix]] automatisch berechnet, aber mit OpenGL3 ist auch diese aus dem Treiber entfernt worden. |
| − | Dies hat | + | Dies hat zur Folge, dass man diesen Schritt selber vollziehen muss, und aufgrund der Wichtigkeit dieser Matrix sollte man versuchen, diesen auch zu verinnerlichen. |
Mit der gl_NormalMatrix kann man ein Normale von dem Texture-Space in den World-Space transformieren. | Mit der gl_NormalMatrix kann man ein Normale von dem Texture-Space in den World-Space transformieren. | ||
| − | Dies ist wie bei der Multiplikation eines Vertex mit der [[gl_ModelViewMatrix]], nur | + | Dies ist wie bei der Multiplikation eines Vertex mit der [[gl_ModelViewMatrix]], nur dass die Konstruktion der gl_NormalMatrix andere Anforderungen hat und deswegen zusätzlich generiert wird. |
| − | Eine Normale ist ein Vektor, welcher die Länge 1 hat und repräsentiert die Flächenausrichtung. | + | Eine Normale ist ein Vektor, welcher die Länge 1 hat, und repräsentiert die Flächenausrichtung. |
Wenn man ein Dreieck auf der X,Y,Z Achse bewegt, dann hat dies keinen Einfluss auf die Werte einer Normale. | Wenn man ein Dreieck auf der X,Y,Z Achse bewegt, dann hat dies keinen Einfluss auf die Werte einer Normale. | ||
Sollte man ein Dreieck aber Rotieren oder Skalieren, dann verändern sich die Werte einer Normale, welcher den Unterschied zwischen gl_NormalMatrix und gl_ModelviewMatrix aus macht. | Sollte man ein Dreieck aber Rotieren oder Skalieren, dann verändern sich die Werte einer Normale, welcher den Unterschied zwischen gl_NormalMatrix und gl_ModelviewMatrix aus macht. | ||
| − | Es gibt einen Spezialfall beim | + | Es gibt einen Spezialfall beim Skalieren: sollte die Skalierung aller Dimensionen mit dem gleichen Wert durchgeführt werden, dann ändert sich die Normale nicht. |
| − | Die gl_NormalMatrix wird errechnet, indem man den Rotationsanteil der Modelview Matrix in eine 3x3 Matrix kopiert, die Inverse errechnet und anschließend die Matrix transponiert. | + | Die gl_NormalMatrix wird errechnet, indem man den Rotationsanteil der Modelview-Matrix in eine 3x3-Matrix kopiert, die Inverse errechnet und anschließend die Matrix transponiert. |
| − | Um nun die Normale in den World-Space zu transformieren kann man folgende Berechnung anwenden. | + | Um nun die Normale in den World-Space zu transformieren, kann man folgende Berechnung anwenden. |
| − | Normal=normalize(gl_NormalMatrix*gl_Normal); | + | Normal=normalize(gl_NormalMatrix*gl_Normal); |
| − | Nach der Multiplikation wird das Ergebnis normalisiert, da eine Normale immer die Länge 1.0 haben muss und durch die Möglichkeit, dass eine Skalierung mit unterschiedlichen Werte auf jeder Achse, dies | + | Nach der Multiplikation wird das Ergebnis normalisiert, da eine Normale immer die Länge 1.0 haben muss und durch die Möglichkeit, dass eine Skalierung mit unterschiedlichen Werte auf jeder Achse, dies sonst nicht gewährleistet wäre. |
| − | Aufgrund der Normalisierung entsteht der vorher erwähnte Sonderfall, bei dem eine Skalierung mit ein und dem selben Skalar | + | Aufgrund der Normalisierung entsteht der vorher erwähnte Sonderfall, bei dem eine Skalierung mit ein und dem selben Skalar keine Änderungen zur Folge hat. |
<source lang="cpp">class TMatrix4x4Float | <source lang="cpp">class TMatrix4x4Float | ||
| Zeile 476: | Zeile 480: | ||
TMatrix3x3Float tnmat; | TMatrix3x3Float tnmat; | ||
float d; | float d; | ||
| − | //Kopiere den Rotations- und Skalierungsanteil aus der Modelview Matrix. | + | //Kopiere den Rotations- und Skalierungsanteil aus der Modelview-Matrix. |
for (unsigned int i=0;i<3;i++) | for (unsigned int i=0;i<3;i++) | ||
for (unsigned int j=0;j<3;j++) | for (unsigned int j=0;j<3;j++) | ||
| Zeile 482: | Zeile 486: | ||
//Inverse mit Hilfe der Determinante berechnen und Transponieren in einem Schritt(im Fall der Rotationsmatrix | //Inverse mit Hilfe der Determinante berechnen und Transponieren in einem Schritt(im Fall der Rotationsmatrix | ||
| − | //ist es nicht wichtig in welcher Reihenfolge Transponieren und Determinieren geschehen.) | + | //ist es nicht wichtig, in welcher Reihenfolge Transponieren und Determinieren geschehen.) |
d=Determinant(m_NormalMatrix); | d=Determinant(m_NormalMatrix); | ||
| Zeile 504: | Zeile 508: | ||
==Projectionview== | ==Projectionview== | ||
| − | Die | + | Die Projektionsmatrix, auch Projectionview genannt, ist die zweite wichtige Matrix in der Renderpipeline. |
| − | Diese Matrix macht den ganzen Zauber | + | Diese Matrix macht den ganzen Zauber der Umwandlung von 3D in 2D erst möglich. |
| − | Wenn die | + | Wenn die Vertices mit der Modelview-Matrix multipliziert wurden, wird nun das Ergebnis mit der Projektionsmatrix multipliziert und wir erhalten Vektoren, dessen X- und Y-Komponente den Bildischrmpunkten entsprechen. Die zwei am häufigsten genutzten Matrizen sind die für die perspektivische und die orthogonale Ansicht. |
===Perspektive=== | ===Perspektive=== | ||
| Zeile 512: | Zeile 516: | ||
[[Bild:GluPerspective_Quads_X.jpg]] | [[Bild:GluPerspective_Quads_X.jpg]] | ||
| − | Die | + | Die perspektivische Ansicht ist eine dreidimensional wirkende Ansicht, welche durch mehrere Faktoren beeinflusst wird. |
[[Bild:GluPerspective.png]] | [[Bild:GluPerspective.png]] | ||
| − | aspect steht für aspect ratio und beschreibt das Bildverhältnis von Höhe und Breite. | + | ''aspect'' steht für aspect ratio und beschreibt das Bildverhältnis von Höhe und Breite. |
| − | Diese ist sehr leicht | + | Diese ist sehr leicht herauszufinden: man dividiert einfach die Breite durch die Höhe, wenn man die Renderausgabe von der Bildschirmbreite abhängig machen möchte, oder umgekehrt für die Bildschirmhöhe. |
| − | f kann durch folgende Formel berechnet werden und bestimmt den Blickwinkel, welcher alle x und y Koordinaten | + | f kann durch folgende Formel berechnet werden und bestimmt den Blickwinkel, welcher alle x- und y-Koordinaten zusammenstaucht oder auseinanderzieht. Dies erkennt man recht schnell, wenn man sich an die Skalierungsmatrix erinnert und das eine Multiplikation mit einem Vektor die x- und y-Komponenten skaliert. |
[[Bild:sichtwinkel.png]] | [[Bild:sichtwinkel.png]] | ||
| − | zNear und zFar sind die Abstände | + | ''zNear'' und ''zFar'' sind die Abstände der Near- und Far-Clipping Plane zur Kamera. Alle Objekte, die den Raum zwischen beiden Ebenen nicht schneiden, werden verworfen und der Rest durchläuft die restliche Renderpipeline. Die Thematik wird in einem späterem Artikel näher erläutet. |
===Orthogonal=== | ===Orthogonal=== | ||
| Zeile 528: | Zeile 532: | ||
[[Bild:Orthomode_Quads.jpg]] | [[Bild:Orthomode_Quads.jpg]] | ||
| − | Die | + | Die orthogonale Ansicht ist eine zweidimensionale Ansicht, welche wie die gewöhnlichen Desktopsysteme wirkt. |
| − | Hierbei werden die Z Koordinaten nicht zur Verschiebung der Bildpunkte | + | Hierbei werden die Z-Koordinaten nicht zur Verschiebung der Bildpunkte in der Tiefe verwendet. |
[[Bild:GlOrtho_Matrix.png]] | [[Bild:GlOrtho_Matrix.png]] | ||
| − | Mit r, l, b, t, f und n sind der rechte, linke, untere und obere Rand, sowie Distanz der far und near clipping plane | + | Mit r, l, b, t, f und n sind der rechte, linke, untere und obere Rand, sowie Distanz der far und near clipping plane des Bildschirmausschnittes gemeint. Die far und near clipping plane sind parallel zum Betrachter ausgerichtete Ebenen. Alles, was zwischen diesen beiden Ebenen liegt, wird gezeichnet und alles außerhalb wird in der Pipeline verworfen. |
=Exkurs in die Optimierung= | =Exkurs in die Optimierung= | ||
| + | |||
==Vektoren== | ==Vektoren== | ||
Man hat oft den Fall, dass man auf der CPU mehrere Werte multiplizieren, dividieren, addieren, subtrahieren muss z.B. bei Bildbearbeitung. | Man hat oft den Fall, dass man auf der CPU mehrere Werte multiplizieren, dividieren, addieren, subtrahieren muss z.B. bei Bildbearbeitung. | ||
| − | Dieses kann man | + | Dieses kann man optimieren, indem man Vektoren verwendet. Dabei wird ein Pixel als Vektor interpretiert und nun kann man alle Farbkanäle mit einen einzigen Aufruf verarbeiten lassen, indem man die Vektoroperationen verwendet. Wenn die Vektoren mit einer CPU-Extension wie SSE oder MMX implementiert wurden, dann werden die vier Komponenten eines Vektors sogar gleichzeitig verarbeitet. Sollte man nur zwei oder drei Komponenten verwenden, dann füllt man die restlichen Komponenten mit 0 auf bzw. ignoriert sie einfach beim Auslesen der Komponenten. |
| + | |||
===Multiplikation=== | ===Multiplikation=== | ||
[[Datei:multiplikation_vektor.png]] | [[Datei:multiplikation_vektor.png]] | ||
| − | Die Multiplikation von | + | Die Multiplikation von zwei Vektoren miteinander ist eigentlich nicht definiert, da es wenig Sinn macht, aber wir haben nun einen Verwendungszweck gefunden und definieren ihn. Bei dieser Operation gilt das gleiche wie bei der Addition und Subtraktion, nur mit einem Mulltiplikationsoperator. Die Bildverarbeitung wird sich mit mehr Geschwindigkeit bedanken. |
<source lang="cpp">class TVector4Float | <source lang="cpp">class TVector4Float | ||
| Zeile 560: | Zeile 566: | ||
[[Datei:division_vektor.png]] | [[Datei:division_vektor.png]] | ||
| − | Bei der Division muss man aufpassen, dass | + | Bei der Division muss man aufpassen, dass keines der Elemente im Divisor 0 ist, da sonst eine Division mit 0 entsteht. Eine Division mit 0 hat ein Interrupt zufolge, welcher das Programm zum beendet. Also sollte man dies vorher überprüfen oder bei einer Division den Aufruf mit einer entsprechenden Routine den Fehler abfangen. Sonst verhält es sich wie bei der Multiplikation. |
<source lang="cpp">class TVector4Float | <source lang="cpp">class TVector4Float | ||
| Zeile 574: | Zeile 580: | ||
};</source> | };</source> | ||
| − | ==Programmiersprache,Compiler und CPU Extension== | + | ==Programmiersprache, Compiler und CPU-Extension== |
| − | Die Optimierung ist von Programmiersprache und Compiler | + | Die Optimierung ist stark von Programmiersprache und Compiler abhängig. Während man mit Delphi, Freepascal und MS VSC++ Compiler nur aufwändig SSE, MMX und weitere CPU Extension implementieren kann, hat der GCC eine Vektorextension und seit Version 4.x auch eine Funktionsoptimierung. Die Vektorextension von GCC ist eine Parsererweiterung, welche einen Typ als ein bestimmten Vektortyp(z.B. Float Länge 4) bestimmt und dann entsprechend alle Operationen in SSE1-4 oder MMX-Code umwandelt. Seit Version 4.x gibt es eine Funktionsoptimierung, welche erlaubt, im Quellcode mehrere Optimierungen gleichzeitig zu nutzen. Die bedeutet, dass man eine Funktion wie Vektor.Magnitude() mehrfach implementiert und dann jeweils eine andere Optimierung aktiviert. Also Vektor.Magnitude_sse(), Vektor.Magnitude_mmx(),... und dann die jeweilige Funktion mit SSE, MMX oder ohne Optimierung markiert. Der Compiler optimiert dann diese Funktion für die jeweilige CPU Extension und man kann dann im Programmcode entsprechend der gegebenen Hardware auf die bestmögliche Funktion umlenken. Dies hat den Vorteil, dass man nur noch eine Binary hat und alle CPUs (mehr Kern, ein Kern, Intel Petium1-4, AMD Athlon und so weiter) der gleichen Architektur optimiert unterstützen kann. Dies ist nützlich, wenn man alte CPUs unterstützen will. Es würde sich also lohnen, wenn man sich viel Ärger und Code sparen will, den Code in GCC als Bibliothek zu implementieren und statisch oder dynamisch zu linken. |
==Templates und Generics== | ==Templates und Generics== | ||
| − | Eine Optimierung die sich bei C++ stark auswirkt sind Templates, da diese die Eigenschaft aufweisen vom Compiler generiert zu werden. Dies bedeutet je nach Qualität des Compilers kann dieser Code starke Performanceschübe bekommen, wenn man die Operationen in Templates verpackt, da der Compiler oft Optimierungen machen kann, die man selber nicht kennt oder gar nicht machen will(Kompatibilität und Übersichtlichkeit). Templates entrollen z.B. konstante | + | Eine Optimierung, die sich bei C++ stark auswirkt, sind Templates, da diese die Eigenschaft aufweisen, vom Compiler generiert zu werden. Dies bedeutet je nach Qualität des Compilers kann dieser Code starke Performanceschübe bekommen, wenn man die Operationen in Templates verpackt, da der Compiler oft Optimierungen machen kann, die man selber nicht kennt oder gar nicht machen will (Kompatibilität und Übersichtlichkeit). Templates entrollen z.B. konstante Zählschleifen und wie schon vorher in den Codeschnipseln zu sehen war, haben wir davon einige in den Vektoroperationen. Das Entrollen von Schleifen entfernt eine Menge Balast (Counter,Prüfung,...), welche sich auf die Performance auswirkt. Templates reduzieren den Codeaufwand, da man viele weitere Implementierungen einspart (Vektor von Typ float, int, unsigned short, unsigned int, double, ...). |
| + | |||
| + | ==Testen, testen, testen== | ||
| + | Wenn man Performancetests macht, dann sollte man verschiedene Tests machen und einer, der teilweise oft unterschätzt wird, ist der Create und Free Test. Sobald man eine Klasse benutzt, wird beim Erstellen des Objektes immer ein Speicher alloziert und dann der Konstruktor aufgerufen, was Zeit kostet. Man sollte also einmal einen Test durchführen, der Vektoren und Matrizen erstellt und zerstört. Die Operation Test sollten die Vektoren und Matrizen vorher erstellen und in der Schleife wiederverwendet werden und nach Beenden des Performance Trackings erst zerstört werden. | ||
| − | + | [[Kategorie:Tutorial|Lineare Algebra]] | |
| − | |||
Aktuelle Version vom 28. November 2013, 16:51 Uhr
(Mehr Informationen/weitere Artikel) Quaternion,Rechtschreibung und Grammatik sowie ein Inhaltscheck fehlen. Die einzelnen Matrizen müssen noch besser erklärt werden. |
Inhaltsverzeichnis
Vorwort
Lineare Algebra ist ein Teilgebiet der Mathematik und beschäftigt sich mit Vektorräumen. Die für OpenGL wichtigen Unterbereiche sind Vektoren und Matrizen. Der größte Teil der 3D-Programmierung beschäftigt sich mit linearer Algebra, daher sollte auch dieser Grundlage eine besondere Aufmerksamkeit gewidmet werden. Sollte der Inhalt vielleicht zu viel für einmal sein, dann wäre es ratsam, ihn in mehreren Etappen zu bewältigen, aber es sollte auf jedenfall vollständig verstanden werden, bevor man sich ernsthaft mit OpenGL auseinandersetzen will.
Trigonometrie
Da später in der Linearen Algebra auf die Trigonometrie zurückgegriffen wird, sollen als erstes die notwendigen Grundlagen in diesem Bereich beleuchtet werden.
Bogenmaß und Gradmaß
Man unterscheidet bei der Darstellung eines Winkels zwischen Bogenmaß(rad) und Gradmaß(deg). Das Bogenmaß wird durch die Konstante Pi beschrieben, wobei der Wertebereich von 0 bis 2*Pi geht. Das Gradmaß ist eine Einteilung, welche von 0 bis 360° abgebildet wird. 0° sind 0, 90° sind 0.5*Pi, 180° sind Pi, 270° sind 3/2*Pi und 360° sind 2*Pi oder auch 0° und 0.
Um vom Bogenmaß ins Gradmaß umzurechnen, kann man folgende Formel verwenden:
Für die Umwandlung vom Bogenmaß ins Gradmaß gilt diese Formel:
Trigonometrische Funktionen
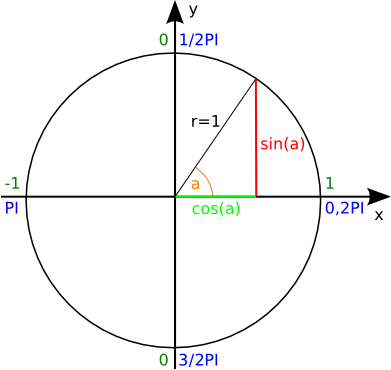
Für das sinnvolle Arbeiten mit Winkelfunktionen benötigen wir einen Einheitskreis. Dies ist ein Kreis, dessen Radius 1 ist und somit eine Reihe von Funktionen zulässt.
Der Einheitskreis ist wie folgt beschriftet. In Blau sind die Bogenmaß Werte angegeben, in dunkelgrün die äquivalenten Werte der Kosinusfunktion und Orange ist der Winkel. Wenn man den Kosinus und Sinus von dem Winkel errechnet, dann erhält man den hellgrünen x- und roten y-Wert. Egal welchen Winkel man in der Sinus- und Kosinusfunktion einsetzt, der Wert wird nie größer 1 oder kleiner -1 werden. Aber halt, wieso?
Trigonometrie im allgemeinen Dreieck
Man unterscheidet in der Trigonometrie zwischen rechtwinkligen Dreiecken und allgemeinen Dreiecken. Die allgemeinen Dreiecke sind allerdings für den weiteren Verlauf des Artikels wichtig und werden deswegen behandelt.
Sinus- und Kosinussatz
Ein wichtige Gleichung, welche später wieder aufgegriffen werden wird, ist der Kosinussatz. Doch zuvor sollte der Sinussatz genauer betrachtet werden.
Durch das Umstellen der Gleichungen kann man die einzelnen Winkel oder Seiten eines Dreiecks erhalten. Hierzu werden entweder zwei Seiten und ein Winkel oder zwei Winkel und eine Seite benötigt.
Der Kosinussatz
ermöglicht es, entweder aus drei gegebenen Seiten die Winkel auszurechnen oder aus zwei Seiten und ihrem Zwischenwinkel die gegenüberliegende Seite zu berechnen.
Eigenschaften und Formeln
Es kann hilfreich sein, eine Sinusfunktion in eine Kosinusfunktion umzuwandeln oder umgekehrt. Hierzu benötigt man die Komplementärformeln, welche wie folgt aussehen:
Um den Rückgabewert der Sinus- oder Kosinusfunktion in den Bogenmaß umzuwandeln, gibt es folgende Umkehrfunktionen.
Es ist zu beachten, dass diese Werte im Bogenmaß zurückgeben und diese für das Gradmaß entsprechend umgerechnet werden müssen.
Außerdem sollte man wissen, dass Sinus und Kosinus keine injektiven Funktionen sind. Das heißt auf deutsch: Wer arccos(cos(a)) berechnet, kann nicht sicher sein, dass das Ergebnis wieder a ist. Um dies nachzuvollziehen, setze man für a z.B. 3/2*pi ein (also 270°). Der Kosinus dieses Winkels ist 0 (siehe Zeichnung oben). Die Funktion arccos bekommt also das Argument 0 übergeben und soll den zugehörigen Winkel ausspucken. Das Problem ist: Es gibt nicht "den" zugehörigen Winkel, sondern zwei (und wenn man Winkel >360° oder <0 zulässt, sind es sogar unendlich viele). Die Arcus-Funktionen geben in diesem Fall den kleinsten Winkel >= 0 aus - also in diesem Fall pi/2 = 90° (siehe Zeichnung oben).
Vektor
Ein Vektor kann mit einem Array oder einer Liste verglichen werden, wenn man z.B. einen 3-dimensionalen Vektor meint, dann wäre es ein Array mit 3 Elementen. Die übliche Schreibweise eines Vektors sieht wie folgt aus.
Eine entsprechende Representation in C++ wäre z.B. folgende:
class TVector4Float
{
public:
float m_Vec[4];
};
OpenGL verwendet auf der Grafikkarte immer 4-dimensionale Vektoren, auch wenn nur 1 oder 3 Elemente benötigt werden. Die restlichen Elemente des Vektors werden dann mit 0 aufgefüllt. Vektoren werden in OpenGL in zwei Arten verwendet, als absoluter und als relativer Wert. Absolute Werte wären z.B. Positionen und Farbwerte, während relative Werte z.B. eine Transformation wäre. Der OpenGL-Vektor sieht wie folgt aus.
Einheitsvektor
Eine besondere Form eines Vektors ist der Einheitsvektor, welcher immer eine Länge von 1 hat. Davon gibt es unendlich viele, nämlich in jede Richtung einen. Wie man aus einem beliebigen Vektor (außer dem Nullvektor) einen Einheitsvektor macht, wird im Abschnitt Normalisierung erläutert. Einheitsvektoren sind als Normalen oder Richtungsvektoren in OpenGL im Einsatz und bilden die Basis für Rotationen.
Addition
Die Addition wird komponentenweise ausgeführt, was bedeutet, man kann sich eine Addition von Vektoren als eine Addition von jeden einzelnen Element mit dem entsprechenden Element im anderem Vektor vorstellen.
Die Addition von Vektoren kann man sich sehr einfach vorstellen, indem man die einzelnen Vektoren als Bewegungsbefehle sieht. Wenn man also 2 Schritte vorwärts, einen Schritt seitwärts laufen soll und danach ein halben Schritt vorwärts und ein Schritt seitwärts, dann kann man diese beiden Befehle auch zu einem Befehl zusammen fassen. Laufe 2 1/2 Schritte vorwärts und 2 Schritte seitwärts und wir stehen am gleichen Punkt und dieser Befehl wäre dann unser Ergebnis Vektor c.
class TVector4Float
{
//...
TVector4Float Addition(TVector4Float b)
{
TVector4Float c;
for (unsigned int i=0;i<4;i++)
c.m_Vec[i]=this->m_Vec[i]+b.m_Vec[i];
return c;
}
};
Subtraktion
Hier gilt gleiches wie bei der Addition, nur dass komponentenweise subtrahiert wird.
Bei der Subtraktion eines Vektors wendet man den ersten Befehl an und läuft z.B. 2 Schritte nach vorne und einen seitwärts, dann wendet man den 2. Schritt an aber wechselt das Vorzeichen jeder einzelnen Komponente. Also wird eine positive Komponente zu einer negativen und eine negative zu einer positiven. Wenn man also einen Schritt seitwärts, nach links, laufen soll, dann läuft man einen Schritt seitwärts, nach rechts, sowie vorwärts statt rückwärts. Man kann eine Subtraktion über eine Addition realisieren, wenn man jede Subtraktion, den rechten Vektor zuvor invertiert und dann addiert.
class TVector4Float
{
//...
TVector4Float Subtraktion(TVector4Float b)
{
TVector4Float c;
for (unsigned int i=0;i<4;i++)
c.m_Vec[i]=this->m_Vec[i]-b.m_Vec[i];
return c;
}
};
Betrag
Magnitude ist der englische Begriff für die Berechnung des Betrags oder auch der Länge eines Vektors. Die Länge des Vektors wird benötigt, wenn man einen Vektor normalisieren will oder feststellen möchte, ob ein Vektor ein Einheitsvektor ist.
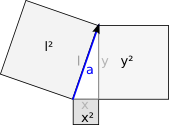
Der Betrag eines Vektors kann über den Satz des Pythagoras ermittelt werden, welcher die Wurzel der Summe der Quadrate aller Komponenten ist. Dies ist natürlich für wenige gut vorstellbar und daher hier mal eine bessere Erklärung. Ein Vektor kann in n Komponenten zerlegt werden, der 4 Komponenten Vektor von OpenGL in 4 Komponenten. Jede Komponente stellt eine Dimension dar, welche x,y,z und w sind. Pythagoras lernt man in der Schule im zweidimensionalen Raum kennen, also wie es im Abbild über diesen Text dargestellt ist. Die Regel besagt, das der Flächeninhalt einer Seite der Summe der anderen entspricht, also l²=x²+y². Diese Flächen sind quadratisch, also hat jede Seite der Fläche die gleiche Kantenlänge. Wenn man die Quadratwurzel von der Fläche zieht, bekommt man also die Kantenlänge. Wenn man nun die Flächen von x,y,z und w summiert erhält man die Fläche l². Zieht man von l² die Quadratwurzel, dann hat man die Kantenlänge l von dem 4Komponenten Vektor, welche als Betrag oder Länge bezeichnet wird. Da bei einem Vektor w=0.0 gesetzt wird, hat diese keinen Einfluss auf diese Operation und wird in den Formeln und auch in der Regel nicht mit hingeschrieben.
class TVector4Float
{
//...
float Betrag(){
float len=0.0;
for (unsigned int i=0;i<4;i++)
len+=this->m_Vec[i]*this->m_Vec[i];
return sqrt(len);
}
};
Skalarprodukt
Das Skalarprodukt erlaubt uns die Berechnung des Winkels zwischen 2 Vektoren. Hierfür müssen allerdings beide Vektoren normalisiert sein, also jeweils einen Betrag von 1 haben. Andernfalls muss dies noch nachträglich getan werden.
Wenn die zwei Vektoren a und b vorliegen, sollte man davon ausgehen, dass der Betrag beider Vektoren jeweils 1 ist. Sollte es nicht der Fall sein, so wie im Bild über diesen Text, dann muss dies durch die Normalisierung nachgeholt werden. Dies passiert, indem man für jeden Vektor den Betrag errechnet und dann den Vektor komponentenweise durch diesen Betrag dividiert. Die oben stehende Formel wird aus dem Kosinussatz abgeleitet und umgestellt. Daraus ergibt sich am Ende, dass die Summe der komponentenweise multiplizierten Vektoren a und b den Kosinus des Winkels ergibt. Es ist wichtig zu beachten, dass nicht der Winkel sondern der Kosinus des Winkels in c wieder zu finden ist. Wenn man den Winkel haben möchte, dann muss man den Arkuskosinus von c berechnen und das Ergebnis ggf. vom Bogenmaß ins Gradmaß umwandeln, um den Winkel (als Delta markiert) zu bekommen.
class TVector4Float
{
//...
float Skalarprodukt(TVector4Float b)
{
float alpha=0.0;
for (unsigned int i=0;i<4;i++)
alpha+=this->m_Vec[i]*b.m_Vec[i];
return c;
}
};
Kreuzprodukt
Das Kreuzprodukt errechnet einen Vektor, der senkrecht zu den Vektoren a und b steht, wenn a und b den selben Ursprung haben. Dieses Verhalten wird genutzt, um die Normale einer Fläche zu errechnen.
Der berechnete Vektor hat wie schon erwähnt die Eigenschaft, dass er senkrecht zu den Vektoren a und b ausgerichtet ist. Dies bedeutet, dass der Winkel zwischen dem berechnetem Vektor und a oder b immer 90° beträgt. Wenn a und b die Verbindungsvektoren von einem Eckpunkt eines Dreiecks zu den beiden anderen sind, dann zeigt der Vektor c senkrecht zum Dreieck und bildet den Richtungsvektor des Dreiecks. Wenn man nun noch diesen Vektor normalisiert, dann erhält man die Flächenormale. Diese hat den Betrag 1 und wird für verschiedene Rendertechniken, sowie Physikberechnungen benötigt. Wenn z.B. ein Lichtstrahl solch ein Dreieck schneidet, dann kann man mit Hilfe des Richtungsvektors (vom Lichstrahl) und der Normale (der Fläche) den Reflektionsvektor berechnen und somit sagen, in welche Richtung sich das Licht weiter bewegen würde. Es ist zu beachten, dass die Reihenfolge, in der man beide Vektoren multipliziert, einen Einfluss auf die Richtung, in die c zeigt, hat. Wenn man a und b tauscht, dann wechseln die Vorzeichen aller Komponenten von c.
class TVector4Float
{
...
TVector4Float Kreuzprodukt(TVector4Float b)
{
TVector4Float c;
unsigned int next,nextnext;
for (unsigned int i=0;i<4;i++)
{
next = (i+1) % 4;//i+1 Modulo 4
nextnext = (i+2) % 4;
c.m_Vec[i] = m_Vec[next]*b.m_Vec[nextnext] - m_Vec[nextnext]*b.m_Vec[next];
}
return c;
}
};
Normalisierung
Bei der Normalisierung wird ein Vektor durch seinen Betrag dividiert und man erhält einen Vektor, der in die gleiche Richtung zeigt, aber auf die Länge 1 skaliert ist.
class TVector4Float
{
//...
TVector4Float Normalisieren(){
TVector4Float c;
c = (*this)/this->Betrag();
return c;
}
};
Matrix
Eine Matrix kann man sich als 2-dimensionalen Array mit n und m Länge vorstellen.
OpenGL verwendet 4x4 große Matrizen und kann aus 4 Vektoren mit einer Länge von 4 konstruiert werden.
class TMatrix4x4Float
{
protected:
TVector4Float m_Matrix[4]; //Erlaubt uns das Nutzen von der eigenen Vektorklasse.
float m_Array[16]; //für die LoadMatrix Funktion von OpenGL
public:
TVector4Float& Vektor(int Index)//Gibt eine Referenz vom Vektor zurück, was wie ein Pointer ist, aber 100% auf ein Speicher zeigt, der existiert.
{
return m_Matrix[Index];
}
T* GetMatrix1DArray()//Liefert den Pointer von der m_Array variable zurück.
{
//Überträgt die Daten von den einzelnen Vektoren in die OpenGL-kompatible Matrix(m_Array).
for (int i=0;i<4;i++)
memcpy(&m_Array[i*4],&m_Matrix[i][0],16);
return &m_Array[0];//Gibt den Pointer auf m_Array zurück.
}
};
Für Matrizen brauchen wir nicht so viele Funktionen wie bei Vektoren, um genau zu sein brauchen wir nur zwei Operationen. Diese Operationen sind das Transponieren und die Multiplikation. Bei der Matrix benötigen wir einige Konstruktionsfunktionen und zwar Identity, Translate, Rotate und Scale Matrix. Diese Matrizen machen die ganze Arbeit für uns, wenn man sich in einem 3D-Raum bewegen möchte, welcher als Modelview Matrix abgebildet wird.
Transponieren
Transponieren wird durch ein großes T über der Matrix dargestellt. Diese Funktion tauscht die Werte einer Matrix miteinander aus, so das aus einer Spalten konstruierten Matrix eine zeilenweise konstruierte Matrix wird. Diese Funktion kann hilfreich sein, wenn man zwischen Direct3D und OpenGL Daten austauschen will, denn nicht jeder nutzt spaltenorientierte Matrizen.
class TMatrix4x4Float
{
//...
void Transponieren()
{
swap(m_Matrix.Vektor(0).m_Vec[1],m_Matrix.Vektor(1).m_Vec[0]); //swap kopiert b in tmp, kopiert a in b und tmp in a
swap(m_Matrix.Vektor(0).m_Vec[2],m_Matrix.Vektor(2).m_Vec[0]);
swap(m_Matrix.Vektor(0).m_Vec[3],m_Matrix.Vektor(3).m_Vec[0]);
swap(m_Matrix.Vektor(1).m_Vec[2],m_Matrix.Vektor(2).m_Vec[1]);
swap(m_Matrix.Vektor(1).m_Vec[3],m_Matrix.Vektor(3).m_Vec[1]);
swap(m_Matrix.Vektor(2).m_Vec[3],m_Matrix.Vektor(3).m_Vec[2]);
}
};
Multiplikation
Multiplikation ist die wichtigste Operation bei Matrizen, wenn wir uns mit OpenGL beschäftigen. Dies liegt daran, dass OpenGL zwei verschiedene Matrizen verwendet, um Vektoren in Bildschirmkoordinaten umzuwandeln. Damit dies funktioniert muss jeder Vektor mit diesen Matrizen jeweils multipliziert werden. Um eine Matrix zu manipulieren, wird diese mit einer konstruierten Matrix multipliziert. Diese Operation die ist meistausgeführte Operation sowohl in der OpenGL-Pipeline als auch in einem Spiel. Seit OpenGL3 gibt es kein Matrizensupport mehr, was bedeutet, dass man diese selber implementieren muss und dann die fertigen Matrizen an OpenGL übergibt. Die lässt viel Raum für Optimierung und kann somit ein OpenGL3-Programm schneller machen als ein OpenGL2-Programm, wenn man zuvor die glTranslate,glRotate und weiteren Funktionen verwendet hat. Es ist also ratsam sich eine sehr performante Bibliothek zu laden oder mit einem Performance Analyzer bewaffnet den eigenen Code zu optimieren.
Multiplikation mit einem Vektor
Um eine Matrix mit einem Vektor zu multiplizieren, braucht man man nur den Vektor[n] von der Matrix mit der Komponente[n] von dem Vektor multiplizieren und die resultierenden Vektoren anschließend addieren. Hierbei wird also ein Vektor mit einer einzelnen Komponente multipliziert, was weiter oben bei den Vektoren erklärt wurde.
class TMatrix4x4Float
{
//...
TVector4Float Multipliziere(TVector4Float V)
{
TVector4Float v=m_Matrix.Vektor(0)*V.m_Vec[0]+m_Matrix.Vektor(1)*V.m_Vec[1]+m_Matrix.Vektor(2)*V.m_Vec[2]+m_Matrix.Vektor(3)*V.m_Vec[3];
return v;
}
};
Multiplikation mit einer Matrix
Es sieht recht aufwändig aus, allerdings kann man es dank der vorigen Matrix-Vektor-Multiplikation auf ein recht übersichtliches Maß runterstreichen. Man braucht dann nur noch die Matrix a jeweils mit einem der Vektoren von Matrix b multiplizieren und hat die Matrix-Matrix-Multiplikation erledigt.
class TMatrix4x4Float
{
//...
TMatrix4x4Float Multiplikation(TMatrix4x4Float M)
{
TMatrix4x4Float M1((*this)*M.Vektor(0)), (*this)*M.Vektor(1), (*this)*M.Vektor(2), (*this)*M.Vektor(3));
return M1;
}
};
Konstruieren von Matrizen
Einheitsmatrix
Die Einheitsmatrix (engl. identity matrix) ist die Initialisierungsmatrix, mit der alle Matrizen belegt werden. Diese ist recht einfach und hat denn Sinn, dass bei einer Multiplikation immer der Wert herauskommt, mit dem diese multipliziert wurde. Wer aufmerksam gelesen hat, der wird nun an Einheitsvektoren denken und liegt richtig. Aufgrund der Beschaffenheit einer Matrix benötigen wir in jeder Reihe und Spalte jeweils ein Element, welches den Wert 1 annimmt und die restlichen nehmen den Wert 0 an. Die sieht dann wie folgt aus:
class TMatrix4x4Float
{
//...
static const TVector4Float Identity[4];//Statische Variable, welche nur einmal existiert.
void LadeIdentity()
{
for (int i=0;i<4;i++)
m_Matrix.Vektor(i)=Identity.m_Vec[i];
}
};
TVector4Float TMatrix4x4Float::Identity[4]={TVector4Float(1.0,0.0,0.0,0.0),TVector4Float(0.0,1.0,0.0,0.0),TVector4Float(0.0,0.0,1.0,0.0),TVector4Float(0.0,0.0,0.0,1.0)};
Translation
Wenn man einen Vektor oder eine Matrix in x,y,z bewegen möchte, dann kann man dies mit einer Transformationsmatrix erreichen. Dazu erstellt man eine Matrix, füllt sie mit der Einheitsmatrix und setzt dann x,y,z in der Matrix mit den zu x,y,z Werten, um die man etwas verschieben möchte.
class TMatrix4x4Float
{
//...
void Translate(float x,float y,float z)
{
TKar_Matrix<KAR_MATH_TYPE> m;
m.Vektor(3).m_Vec[0]=x;
m.Vektor(3).m_Vec[1]=y;
m.Vektor(3).m_Vec[2]=z;
(*this)*=m;
}
};
Rotation
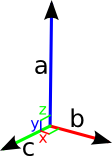
Das Bewegen auf den drei Achsen ist allerdings oft nicht ausreichend und deswegen gibt es auch eine Rotationsmatrix. Die Rotationsmatrix wird durch drei Vektoren beschrieben, welche jeweils für die x-, y- und z-Achse zuständig sind. Man kann die Rotation der einzelnen Achsen in einem Schritt erledigen oder in 3 einzelne aufteilen. Um die Rotationsmatrix besser zu verstehen, werden erst einmal alle Achsen einzeln betrachtet.
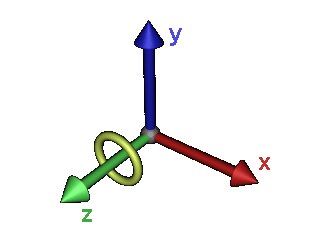
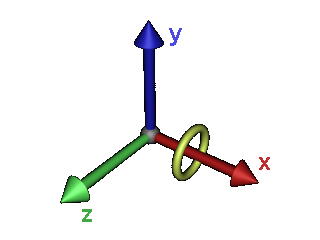
Drehen um die Z-Achse
Der Z-Achsen-Einheitsvektor(3. Spalte=0.0, 0.0, 1.0, 0.0) bleibt bei der Rotation unverändert - man nehme einen Finger, deute damit nach vorne. Nun drehe man diesen Finger um seine eigene Achse, wohin zeigt er? In die selbe Richtung wie vor der Drehung? Damit entspricht Z-Achsen-Einheitsvektor auch der vorletzen Spalte der Matrix: (0.0, 0.0, 1.0, 0.0)
Der X-Achsen-Einheitsvektor(1. Spalte=1.0, 0.0, 0.0 0.0) dreht sich hingegen mit. Trigonometrie findet der Lösung Spur. Ein Blick auf das Bild zum Einheitskreis zeigt, dass wir gerade das gleiche Problem für X und Y zu bewältigen haben: Die Rotationsachse ist in beiden Fällen die Z-Achse. Der Einheitsvektor, der gedreht wird, ist der X-Achsen-Einheitsvektor also:
x = cos(ß)
y = sin(ß)
womit der Inhalt der ersten Spalte der Matrix kennen: (cos(ß), sin(ß), 0.0, 0.0)
Dies kann man auch auf den Y-Achsen-Einheitsvektor(2. Spalte=0.0, 1.0, 0.0, 0.0) übertragen, man muss nur beachten, in welcher Weise man dafür x und y vertauschen muss:
x = -sin(ß)
y = cos(ß)
So ergibt sich für die zweite Spalte: (-sin(ß), cos(ß), 0.0, 0.0)
Nun kann man die Rotationsmatrix für die Rotation auf der Z-Achse beschreiben, die Matrix findet man am Anfang des Abschnittes.
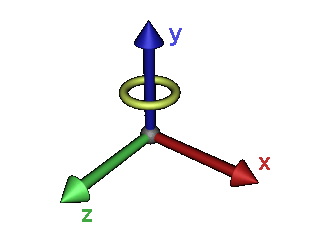
Drehen um die Y-Achse
Die Berechnung der Matrix wird auf die gleiche Weise ermittelt wie bei der Berechnung der Rotationsmatrix für die Drehung um die Z-Achse.
Drehen um die X-Achse
Rotation um alle Achsen mit einer Matrix
Es ist recht aufwändig für die CPU und für den Programmierer, immer drei Rotationen auszuführen, deswegen hat man diese auch zu einer einzigen Operation zusammengefasst. Die Matrizen werden einfach miteinander multipliziert und es kommt eine Rotationsmatrix heraus, welche drei Eingabeparameter benötigt, alpha, beta und gamma sind dabei die Winkel für X-,Y- und Z-Achse.
Eine weitere Möglichkeit, um eine Rotationsmatrix zu erstellen, wäre das Nutzen eines Richtungsvektors und eines Winkels. Hierbei wird der Winkel auf den Richtungsvektor angewendet, wenn man also als Vektor (1,0,0) verwendet, dann hat man eine Rotation auf der X-Achse, (0,1,0) Y-Achse und (0,0,1) für die Z-Achse. Man kann nun auch Vektoren wie (1,1,1) angeben, wobei die Funktion diesen Vektor dann normalisieren wird, damit er noch auf das Einheitskreis System funktioniert. Dieser Vektor ist nicht äquivalent mit dem Rotieren von X-,Y- und Z-Achse nacheinander. Der Vorteil hierbei liegt in der Kompaktheit des Codes und man kann auf Algorithmen zurückgreifen, die vor OpenGL3 entwickelt wurden, da der OpenGL-Treiber früher die Rotation über diese Variante implementiert hatte.
class TMatrix4x4Float
{
//...
void Rotiere(float w,float x,float y,float z)
{
TMatrix4Float m;
float rad=DegToRad(w);
float c=cos(rad);
float ic=1.0-c;
float s=sin(rad);
TVector4Float v(x,y,z,0.0);
float mag=sqrt((v*v).Summe());
if (mag<=1.0e-4)
return;
v.m_Vec[0]=x/mag;
v.m_Vec[1]=y/mag;
v.m_Vec[2]=z/mag;
m.Vektor(0).m_Vec[0]=(v.m_Vec[0]*v.m_Vec[0]*ic)+c;
m.Vektor(0).m_Vec[1]=(v.m_Vec[0]*v.m_Vec[1]*ic)+(v.m_Vec[2]*s);
m.Vektor(0).m_Vec[2]=(v.m_Vec[0]*v.m_Vec[2]*ic)-(v.m_Vec[1]*s);
m.Vektor(1).m_Vec[0]=(v.m_Vec[0]*v.m_Vec[1]*ic)-(v.m_Vec[2]*s);
m.Vektor(1).m_Vec[1]=(v.m_Vec[1]*v.m_Vec[1]*ic)+c;
m.Vektor(1).m_Vec[2]=(v.m_Vec[1]*v.m_Vec[2]*ic)+(v.m_Vec[0]*s);
m.Vektor(2).m_Vec[0]=(v.m_Vec[0]*v.m_Vec[2]*ic)+(v.m_Vec[1]*s);
m.Vektor(2).m_Vec[1]=(v.m_Vec[1]*v.m_Vec[2]*ic)-(v.m_Vec[0]*s);
m.Vektor(2).m_Vec[2]=(v.m_Vec[2]*v.m_Vec[2]*ic)+c;
*this*=m;
}
};
Skalieren
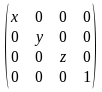
Die Skalierung ist eine sehr einfache Matrix, in der für die 1 des Einheitsvektors der entsprechende Skalierungsfaktor angegeben wird. Wenn man die Matrix mit einem Vektor multipliziert, dann werden X, Y und Z des Vektors mit den x- ,y- und z-Werten in der Skalierungsmatrix multipliziert und damit skaliert. Wenn man etwas größer machen will, dann wird der Wert entsprechend über 1.0 gewählt (z.B. 2.0 wäre doppelte Größe), und für eine Verkleinerung würde man ein Wert zwischen 1.0 und 0.0 wählen. Der Wert 0.5 würde z.B. eine Division durch 2 bedeuten, also 3*0.5=1.5. Der 4. Einheitsvektor wird so belassen, da wir diesen nur aus Kompatibilitätsgründen zu den 4-Komponenten-Vektoren benötigen.
Vom Vektor zur Bildschirmkoordinate
Auf in den Endspurt! Alle mathematischen Formeln und Funktionen benötigen wir, um die letzten zwei Punkte behandeln zu können. Die Rede ist von der Umwandlung eines Vektors im 3D-Raum in den 2D-Raum, auf dem Bildschirm. In Rahmen dieses Artikel wird nur auf die Transformation der Vektoren eingegangen und in einem späterem Artikel dann die weiteren Zwischenschritte zum Zeichnen einer Geometrie.
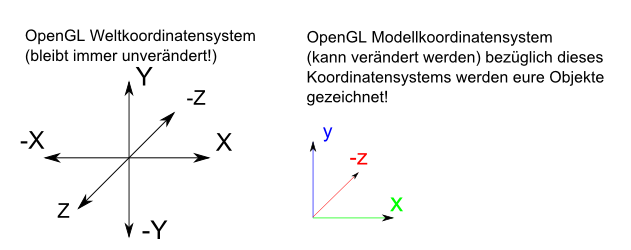
Modelview
Die Modelview kann man sich wie ein 3D-Unterraum vorstellen oder einer Transformation des Raumes. Die Modelview sorgt dafür, dass alle Vektoren, die mit dieser multipliziert werden, zu dieser Modelview ausgerichtet werden und die Modelview ist relativ zur Welt ausgerichtet. Dies bedeutet, wenn man für jedes Objekt eine Modelview erzeugt, dann kann dieses Objekt relativ zur Welt ausgerichtet werden, sobald man die Vektoren des Objektes mit der Modelview multipliziert. Wieso richtet man die Vektoren nicht gleich zur Welt aus, statt den Umweg über die Modelview Matrix zu gehen? Die Antwort ist schlicht "Optimierung". Es wäre zu langsam, wenn man jeden Renderdurchgang jedes einzelne Vertex im Speicher lesen müsste, die neue Position berechnen, im Speicher updaten und in der Pipeline weiter zu arbeiten. Es ist auch speichereffizienter, da z.B. gleiche Objekte nur einmal in den Speicher abgelegt werden müssen und nur zwei unterschiedliche Modelview-Matrizen benötigt werden.
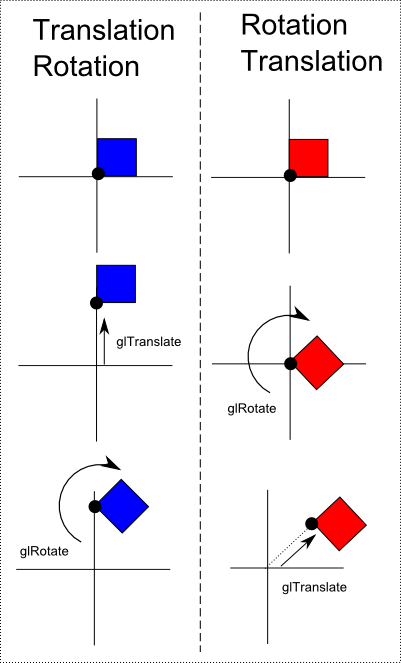
Im rechten Bild kann man zwei aufeinanderfolgende Befehlsketten sehen, die Transformationen auf ein Objekt anwenden. Dieses Bild soll noch einmal verdeutlichen, dass das Anwenden von Befehlen auf eine Modelview-Matrix nicht kommutativ ist (a*b ist im Allgemeinen nicht das gleiche wie b*a).
Während vor OpenGL3 die Modelview-Matrix von den OpenGL-Treibern verwaltet wurde, muss dies ab OpenGL3 vom Nutzer gemacht werden und auch das Aktualisieren in der Renderpipeline muss nun vom Entwickler übernommen werden. Wie dies funktioniert, wird in einem späteren Artikel erklärt. Es ist nur noch wichtig zu sagen, dass die GPU diese Matrix mit jeden Vertex multipliziert, der durch die Renderpipeline geschickt wird.
Normal-Matrix
Die Normal-Matrix wurde vor OpenGL3 als gl_NormalMatrix automatisch berechnet, aber mit OpenGL3 ist auch diese aus dem Treiber entfernt worden. Dies hat zur Folge, dass man diesen Schritt selber vollziehen muss, und aufgrund der Wichtigkeit dieser Matrix sollte man versuchen, diesen auch zu verinnerlichen. Mit der gl_NormalMatrix kann man ein Normale von dem Texture-Space in den World-Space transformieren. Dies ist wie bei der Multiplikation eines Vertex mit der gl_ModelViewMatrix, nur dass die Konstruktion der gl_NormalMatrix andere Anforderungen hat und deswegen zusätzlich generiert wird.
Eine Normale ist ein Vektor, welcher die Länge 1 hat, und repräsentiert die Flächenausrichtung. Wenn man ein Dreieck auf der X,Y,Z Achse bewegt, dann hat dies keinen Einfluss auf die Werte einer Normale. Sollte man ein Dreieck aber Rotieren oder Skalieren, dann verändern sich die Werte einer Normale, welcher den Unterschied zwischen gl_NormalMatrix und gl_ModelviewMatrix aus macht. Es gibt einen Spezialfall beim Skalieren: sollte die Skalierung aller Dimensionen mit dem gleichen Wert durchgeführt werden, dann ändert sich die Normale nicht. Die gl_NormalMatrix wird errechnet, indem man den Rotationsanteil der Modelview-Matrix in eine 3x3-Matrix kopiert, die Inverse errechnet und anschließend die Matrix transponiert.
Um nun die Normale in den World-Space zu transformieren, kann man folgende Berechnung anwenden.
Normal=normalize(gl_NormalMatrix*gl_Normal);
Nach der Multiplikation wird das Ergebnis normalisiert, da eine Normale immer die Länge 1.0 haben muss und durch die Möglichkeit, dass eine Skalierung mit unterschiedlichen Werte auf jeder Achse, dies sonst nicht gewährleistet wäre. Aufgrund der Normalisierung entsteht der vorher erwähnte Sonderfall, bei dem eine Skalierung mit ein und dem selben Skalar keine Änderungen zur Folge hat.
class TMatrix4x4Float
{
//...
protected:
TMatrix3x3Float m_NormalMatrix;
public:
TMatrix3x3Float& NormalMatrix()
{
TMatrix3x3Float tnmat;
float d;
//Kopiere den Rotations- und Skalierungsanteil aus der Modelview-Matrix.
for (unsigned int i=0;i<3;i++)
for (unsigned int j=0;j<3;j++)
m_NormalMatrix.Value[i*3+j]=this->Value[i*4+j];
//Inverse mit Hilfe der Determinante berechnen und Transponieren in einem Schritt(im Fall der Rotationsmatrix
//ist es nicht wichtig, in welcher Reihenfolge Transponieren und Determinieren geschehen.)
d=Determinant(m_NormalMatrix);
tnmat[0]=m_NormalMatrix[4]*m_NormalMatrix[8]-m_NormalMatrix[5]*m_NormalMatrix[7];
tnmat[3]=m_NormalMatrix[5]*m_NormalMatrix[6]-m_NormalMatrix[3]*m_NormalMatrix[8];
tnmat[6]=m_NormalMatrix[3]*m_NormalMatrix[7]-m_NormalMatrix[4]*m_NormalMatrix[6];
tnmat[1]=m_NormalMatrix[2]*m_NormalMatrix[7]-m_NormalMatrix[5]*m_NormalMatrix[8];
tnmat[4]=m_NormalMatrix[0]*m_NormalMatrix[8]-m_NormalMatrix[2]*m_NormalMatrix[6];
tnmat[7]=m_NormalMatrix[1]*m_NormalMatrix[6]-m_NormalMatrix[1]*m_NormalMatrix[7];
tnmat[2]=m_NormalMatrix[1]*m_NormalMatrix[5]-m_NormalMatrix[2]*m_NormalMatrix[4];
tnmat[5]=m_NormalMatrix[2]*m_NormalMatrix[3]-m_NormalMatrix[0]*m_NormalMatrix[5];
tnmat[8]=m_NormalMatrix[0]*m_NormalMatrix[4]-m_NormalMatrix[1]*m_NormalMatrix[3];
for (unsigned int i=0;i<3;i++)
for (unsigned int j=0;j<3;j++)
m_NormalMatrix[i*3+j]=tnmat[i*3+j]/d;
return tnmat;
}
Projectionview
Die Projektionsmatrix, auch Projectionview genannt, ist die zweite wichtige Matrix in der Renderpipeline. Diese Matrix macht den ganzen Zauber der Umwandlung von 3D in 2D erst möglich. Wenn die Vertices mit der Modelview-Matrix multipliziert wurden, wird nun das Ergebnis mit der Projektionsmatrix multipliziert und wir erhalten Vektoren, dessen X- und Y-Komponente den Bildischrmpunkten entsprechen. Die zwei am häufigsten genutzten Matrizen sind die für die perspektivische und die orthogonale Ansicht.
Perspektive
Die perspektivische Ansicht ist eine dreidimensional wirkende Ansicht, welche durch mehrere Faktoren beeinflusst wird.
aspect steht für aspect ratio und beschreibt das Bildverhältnis von Höhe und Breite. Diese ist sehr leicht herauszufinden: man dividiert einfach die Breite durch die Höhe, wenn man die Renderausgabe von der Bildschirmbreite abhängig machen möchte, oder umgekehrt für die Bildschirmhöhe. f kann durch folgende Formel berechnet werden und bestimmt den Blickwinkel, welcher alle x- und y-Koordinaten zusammenstaucht oder auseinanderzieht. Dies erkennt man recht schnell, wenn man sich an die Skalierungsmatrix erinnert und das eine Multiplikation mit einem Vektor die x- und y-Komponenten skaliert.
zNear und zFar sind die Abstände der Near- und Far-Clipping Plane zur Kamera. Alle Objekte, die den Raum zwischen beiden Ebenen nicht schneiden, werden verworfen und der Rest durchläuft die restliche Renderpipeline. Die Thematik wird in einem späterem Artikel näher erläutet.
Orthogonal
Die orthogonale Ansicht ist eine zweidimensionale Ansicht, welche wie die gewöhnlichen Desktopsysteme wirkt. Hierbei werden die Z-Koordinaten nicht zur Verschiebung der Bildpunkte in der Tiefe verwendet.
Mit r, l, b, t, f und n sind der rechte, linke, untere und obere Rand, sowie Distanz der far und near clipping plane des Bildschirmausschnittes gemeint. Die far und near clipping plane sind parallel zum Betrachter ausgerichtete Ebenen. Alles, was zwischen diesen beiden Ebenen liegt, wird gezeichnet und alles außerhalb wird in der Pipeline verworfen.
Exkurs in die Optimierung
Vektoren
Man hat oft den Fall, dass man auf der CPU mehrere Werte multiplizieren, dividieren, addieren, subtrahieren muss z.B. bei Bildbearbeitung.
Dieses kann man optimieren, indem man Vektoren verwendet. Dabei wird ein Pixel als Vektor interpretiert und nun kann man alle Farbkanäle mit einen einzigen Aufruf verarbeiten lassen, indem man die Vektoroperationen verwendet. Wenn die Vektoren mit einer CPU-Extension wie SSE oder MMX implementiert wurden, dann werden die vier Komponenten eines Vektors sogar gleichzeitig verarbeitet. Sollte man nur zwei oder drei Komponenten verwenden, dann füllt man die restlichen Komponenten mit 0 auf bzw. ignoriert sie einfach beim Auslesen der Komponenten.
Multiplikation
Die Multiplikation von zwei Vektoren miteinander ist eigentlich nicht definiert, da es wenig Sinn macht, aber wir haben nun einen Verwendungszweck gefunden und definieren ihn. Bei dieser Operation gilt das gleiche wie bei der Addition und Subtraktion, nur mit einem Mulltiplikationsoperator. Die Bildverarbeitung wird sich mit mehr Geschwindigkeit bedanken.
class TVector4Float
{
//...
TVector4Float Multiplikation(TVector4Float b)
{
TVector4Float c;
for (unsigned int i=0;i<4;i++)
c.m_Vec[i]=this->m_Vec[i]*b.m_Vec[i];
return c;
}
};
Division
Bei der Division muss man aufpassen, dass keines der Elemente im Divisor 0 ist, da sonst eine Division mit 0 entsteht. Eine Division mit 0 hat ein Interrupt zufolge, welcher das Programm zum beendet. Also sollte man dies vorher überprüfen oder bei einer Division den Aufruf mit einer entsprechenden Routine den Fehler abfangen. Sonst verhält es sich wie bei der Multiplikation.
class TVector4Float
{
//...
TVector4Float Division(TVector4Float b)
{
TVector4Float c;
for (unsigned int i=0;i<4;i++)
c.m_Vec[i]=this->m_Vec[i]/b.m_Vec[i];
return c;
}
};
Programmiersprache, Compiler und CPU-Extension
Die Optimierung ist stark von Programmiersprache und Compiler abhängig. Während man mit Delphi, Freepascal und MS VSC++ Compiler nur aufwändig SSE, MMX und weitere CPU Extension implementieren kann, hat der GCC eine Vektorextension und seit Version 4.x auch eine Funktionsoptimierung. Die Vektorextension von GCC ist eine Parsererweiterung, welche einen Typ als ein bestimmten Vektortyp(z.B. Float Länge 4) bestimmt und dann entsprechend alle Operationen in SSE1-4 oder MMX-Code umwandelt. Seit Version 4.x gibt es eine Funktionsoptimierung, welche erlaubt, im Quellcode mehrere Optimierungen gleichzeitig zu nutzen. Die bedeutet, dass man eine Funktion wie Vektor.Magnitude() mehrfach implementiert und dann jeweils eine andere Optimierung aktiviert. Also Vektor.Magnitude_sse(), Vektor.Magnitude_mmx(),... und dann die jeweilige Funktion mit SSE, MMX oder ohne Optimierung markiert. Der Compiler optimiert dann diese Funktion für die jeweilige CPU Extension und man kann dann im Programmcode entsprechend der gegebenen Hardware auf die bestmögliche Funktion umlenken. Dies hat den Vorteil, dass man nur noch eine Binary hat und alle CPUs (mehr Kern, ein Kern, Intel Petium1-4, AMD Athlon und so weiter) der gleichen Architektur optimiert unterstützen kann. Dies ist nützlich, wenn man alte CPUs unterstützen will. Es würde sich also lohnen, wenn man sich viel Ärger und Code sparen will, den Code in GCC als Bibliothek zu implementieren und statisch oder dynamisch zu linken.
Templates und Generics
Eine Optimierung, die sich bei C++ stark auswirkt, sind Templates, da diese die Eigenschaft aufweisen, vom Compiler generiert zu werden. Dies bedeutet je nach Qualität des Compilers kann dieser Code starke Performanceschübe bekommen, wenn man die Operationen in Templates verpackt, da der Compiler oft Optimierungen machen kann, die man selber nicht kennt oder gar nicht machen will (Kompatibilität und Übersichtlichkeit). Templates entrollen z.B. konstante Zählschleifen und wie schon vorher in den Codeschnipseln zu sehen war, haben wir davon einige in den Vektoroperationen. Das Entrollen von Schleifen entfernt eine Menge Balast (Counter,Prüfung,...), welche sich auf die Performance auswirkt. Templates reduzieren den Codeaufwand, da man viele weitere Implementierungen einspart (Vektor von Typ float, int, unsigned short, unsigned int, double, ...).
Testen, testen, testen
Wenn man Performancetests macht, dann sollte man verschiedene Tests machen und einer, der teilweise oft unterschätzt wird, ist der Create und Free Test. Sobald man eine Klasse benutzt, wird beim Erstellen des Objektes immer ein Speicher alloziert und dann der Konstruktor aufgerufen, was Zeit kostet. Man sollte also einmal einen Test durchführen, der Vektoren und Matrizen erstellt und zerstört. Die Operation Test sollten die Vektoren und Matrizen vorher erstellen und in der Schleife wiederverwendet werden und nach Beenden des Performance Trackings erst zerstört werden.