Tutorial Kollision1: Unterschied zwischen den Versionen
Flash (Diskussion | Beiträge) K (Pascaltags ->CppTags) |
K (→Nun zur Kollision: Rechtschreibfehler korrigiert, Ebene verlinkt) |
||
| (4 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 123: | Zeile 123: | ||
Wir brauchen also zwei Vektor-Variablen, die wir nach dem Programmstart auf geeignete Anfangswerte setzen: | Wir brauchen also zwei Vektor-Variablen, die wir nach dem Programmstart auf geeignete Anfangswerte setzen: | ||
| − | <cpp> | + | <source lang="cpp"> |
TVector position; | TVector position; | ||
TVector velocity; | TVector velocity; | ||
| Zeile 133: | Zeile 133: | ||
velocity.y = 0.0 // bleibt immer 0, zweidimensional | velocity.y = 0.0 // bleibt immer 0, zweidimensional | ||
velocity.z = -0.5 // Vorwärtsbewegung | velocity.z = -0.5 // Vorwärtsbewegung | ||
| − | </ | + | </source> |
Die Werte müssen wir natürlich anpassen. Vor dem Zeichnen der Kugel wird in jedem Frame die Position aktualisiert: | Die Werte müssen wir natürlich anpassen. Vor dem Zeichnen der Kugel wird in jedem Frame die Position aktualisiert: | ||
| − | <cpp> | + | <source lang="cpp"> |
position = AddVectors (position, ScaleVector (timestep, velocity)); | position = AddVectors (position, ScaleVector (timestep, velocity)); | ||
| − | </ | + | </source> |
Wenn wir das Programm starten, rollt die Kugel, lässt sich aber von der Bande nicht aufhalten und verschwindet in der unendlichen Weite. Vielleicht wird sie irgendwann den Mars umkreisen oder in der Sonne verglühen, wobei wir dafür erst den passenden Code schreiben müssten. ;) | Wenn wir das Programm starten, rollt die Kugel, lässt sich aber von der Bande nicht aufhalten und verschwindet in der unendlichen Weite. Vielleicht wird sie irgendwann den Mars umkreisen oder in der Sonne verglühen, wobei wir dafür erst den passenden Code schreiben müssten. ;) | ||
| Zeile 155: | Zeile 155: | ||
Was ist zu tun? Genauer: Wo müssen wir die Kugel abfangen und ihr mitteilen, dass es beim nächsten Mal in anderer Richtung weitergeht? Wir können das erledigen, nachdem die Kugel die Grenzlinie überschritten hat, oder wir machen das vorher, indem wir den anstehenden Bewegungsschritt nur probehalber durchführen und ggfs. unterlassen? Beides ist nicht ganz sauber, und nur, wenn die Kugel sehr langsam rollt und die Bewegungsschritte entsprechend klein sind, fällt es nicht auf. Wenn wir genau sein wollen, müssen wir ein wenig weiter ausholen und den Berührungspunkt auf der weißen Linie finden. Nennen wir ihn '''Intersektionspunkt''', obwohl der eigentliche Intersektionspunkt direkt an der Bande liegt. | Was ist zu tun? Genauer: Wo müssen wir die Kugel abfangen und ihr mitteilen, dass es beim nächsten Mal in anderer Richtung weitergeht? Wir können das erledigen, nachdem die Kugel die Grenzlinie überschritten hat, oder wir machen das vorher, indem wir den anstehenden Bewegungsschritt nur probehalber durchführen und ggfs. unterlassen? Beides ist nicht ganz sauber, und nur, wenn die Kugel sehr langsam rollt und die Bewegungsschritte entsprechend klein sind, fällt es nicht auf. Wenn wir genau sein wollen, müssen wir ein wenig weiter ausholen und den Berührungspunkt auf der weißen Linie finden. Nennen wir ihn '''Intersektionspunkt''', obwohl der eigentliche Intersektionspunkt direkt an der Bande liegt. | ||
| − | Damit sind wir schon mitten drin im Kollisionszirkel. Es geht | + | Damit sind wir schon mitten drin im Kollisionszirkel. Es geht darum, den Schnittpunkt eines Strahls mit einer [[Ebene]] zu berechnen ''(ray-plane intersection)''. Der Strahl ist nichts anderes als der Bewegungsvektor der Kugel, der von der Kugelposition wegzeigt. Und die Ebene müssen wir uns senkrecht auf der weißen Linie vorstellen, wie eine unsichtbare Wand. |
Die mathematischen Hintergründe wollen wir uns ersparen, hier die Funktion, die den Intersektionspunkt ausrechnet: | Die mathematischen Hintergründe wollen wir uns ersparen, hier die Funktion, die den Intersektionspunkt ausrechnet: | ||
| − | <cpp> | + | <source lang="cpp"> |
double PlaneIntersect (TVector pOrigin, TVector pNormal, TVector sPosition, TVector sDir) | double PlaneIntersect (TVector pOrigin, TVector pNormal, TVector sPosition, TVector sDir) | ||
{ | { | ||
| Zeile 167: | Zeile 167: | ||
return -(num / denom); | return -(num / denom); | ||
} | } | ||
| − | </ | + | </source> |
''pOrigin'' ist irgendein Punkt auf der Ebene und damit auf der weißen Hilfslinie. Es dürfte kein Problem sein, irgendeinen geeigneten Punkt zu finden. ''pNormal'' ist die Normale der Ebene, ein Vektor, den wir ganz einfach im Kopf ausrechnen können. Nehmen wir dazu die linke Begrenzungsebene. Aus der Sicht der Kugel zeigt die Normale nach rechts, also ist der Vektor (1, 0, 0). Ähnliches gilt für die anderen drei Ebenen. | ''pOrigin'' ist irgendein Punkt auf der Ebene und damit auf der weißen Hilfslinie. Es dürfte kein Problem sein, irgendeinen geeigneten Punkt zu finden. ''pNormal'' ist die Normale der Ebene, ein Vektor, den wir ganz einfach im Kopf ausrechnen können. Nehmen wir dazu die linke Begrenzungsebene. Aus der Sicht der Kugel zeigt die Normale nach rechts, also ist der Vektor (1, 0, 0). Ähnliches gilt für die anderen drei Ebenen. | ||
| Zeile 179: | Zeile 179: | ||
An der Bande lassen wir die Kugel zunächst liegen, versäumen aber nicht, die Richtung so zu verändern, dass der Aufprallwinkel gleich dem Rückprallwinkel ist. Auch das ist kein Problem, schauen wir wieder auf die linke Bande. Es ändert sich hier nur die x-Richtung, während die Fortbewegung in z-Richtung gleich bleibt. Also stülpen wir den x-Wert des Bewegungsvektors um: | An der Bande lassen wir die Kugel zunächst liegen, versäumen aber nicht, die Richtung so zu verändern, dass der Aufprallwinkel gleich dem Rückprallwinkel ist. Auch das ist kein Problem, schauen wir wieder auf die linke Bande. Es ändert sich hier nur die x-Richtung, während die Fortbewegung in z-Richtung gleich bleibt. Also stülpen wir den x-Wert des Bewegungsvektors um: | ||
| − | <cpp> | + | <source lang="cpp"> |
velocity.x = - velocity.x; | velocity.x = - velocity.x; | ||
| − | </ | + | </source> |
Mit den anderen Banden verfahren wir analog. Es ist aber wichtig, dass wir immer '''alle vier Banden''' überprüfen. Es kann nämlich sein, dass die Kugel auf eine Ecke zusteuert und gleichzeitig mit zwei Banden in Konflikt gerät. Dann müssen in ein- und demselben Frame zwei Richtungen umgedreht werden. Wenn wir feststellen, dass die Kugel gelegentlich außerhalb des Käfigs hin- und herzittert und nicht wieder hinein will, haben wir diesen Punkt nicht beachtet. | Mit den anderen Banden verfahren wir analog. Es ist aber wichtig, dass wir immer '''alle vier Banden''' überprüfen. Es kann nämlich sein, dass die Kugel auf eine Ecke zusteuert und gleichzeitig mit zwei Banden in Konflikt gerät. Dann müssen in ein- und demselben Frame zwei Richtungen umgedreht werden. Wenn wir feststellen, dass die Kugel gelegentlich außerhalb des Käfigs hin- und herzittert und nicht wieder hinein will, haben wir diesen Punkt nicht beachtet. | ||
| Zeile 195: | Zeile 195: | ||
In der Abbildung steckt alles, was wir zur Lösung des Problems brauchen. Wieder haben wir die weiße Linie, die uns erlaubt, mit dem Mittelpunkt der Kugel zu rechnen, und natürlich ist der äußere Kreis um den Radius der Kugel größer als der eigentliche Kollisionskörper. Wir sehen die gelb eingezeichnete Tangente, an der wir die Reflexion vornehmen. Doch vorher müssen wir wieder den Intersektionspunkt haben, worauf der blaue Pfeil zeigt. Hier nun die Funktion, die uns den Punkt liefert: | In der Abbildung steckt alles, was wir zur Lösung des Problems brauchen. Wieder haben wir die weiße Linie, die uns erlaubt, mit dem Mittelpunkt der Kugel zu rechnen, und natürlich ist der äußere Kreis um den Radius der Kugel größer als der eigentliche Kollisionskörper. Wir sehen die gelb eingezeichnete Tangente, an der wir die Reflexion vornehmen. Doch vorher müssen wir wieder den Intersektionspunkt haben, worauf der blaue Pfeil zeigt. Hier nun die Funktion, die uns den Punkt liefert: | ||
| − | <cpp> | + | <source lang="cpp"> |
double CircleIntersect (TVector center, double radius, | double CircleIntersect (TVector center, double radius, | ||
TVector sPosition, TVector sDir) | TVector sPosition, TVector sDir) | ||
| Zeile 208: | Zeile 208: | ||
return v - sqrt (d); | return v - sqrt (d); | ||
} | } | ||
| − | </ | + | </source> |
Die ersten beiden Parameter beschreiben den Kollisionskreis (oder Zylinder) und dürften selbsterklärend sein; die beiden anderen Parameter sind dieselben wie bei der Funktion weiter oben. Auch das Ergebnis wird in gleicher Weise verwendet. Halt, eines ist zu beachten: '''sDir muss nun auf jeden Fall normalisiert sein!''' | Die ersten beiden Parameter beschreiben den Kollisionskreis (oder Zylinder) und dürften selbsterklärend sein; die beiden anderen Parameter sind dieselben wie bei der Funktion weiter oben. Auch das Ergebnis wird in gleicher Weise verwendet. Halt, eines ist zu beachten: '''sDir muss nun auf jeden Fall normalisiert sein!''' | ||
| Zeile 216: | Zeile 216: | ||
Der '''Reflexionswinkel''' lässt sich leider nicht mehr ganz so einfach berechnen wie bei der Kollision an der Bande. Die Tangente ist ja nicht nach x oder z ausgerichtet, sondern kann irgendwie liegen. Aber auch hierfür gibt es eine praktische Funktion: | Der '''Reflexionswinkel''' lässt sich leider nicht mehr ganz so einfach berechnen wie bei der Kollision an der Bande. Die Tangente ist ja nicht nach x oder z ausgerichtet, sondern kann irgendwie liegen. Aber auch hierfür gibt es eine praktische Funktion: | ||
| − | <cpp> | + | <source lang="cpp"> |
TVector ReflectVector (TVector a, TVector norm) | TVector ReflectVector (TVector a, TVector norm) | ||
{ | { | ||
| Zeile 228: | Zeile 228: | ||
return res; | return res; | ||
} | } | ||
| − | </ | + | </source> |
| − | a ist der normalisierte Bewegungsvektor, der auf den Intersektionspunkt zeigt, und norm ist die Normale der Tangente bzw. der Ebene, die sie repräsentiert. Diese Normale lässt sich schnell aus dem Mittelpunkt des Kreises und dem Intersektionspunkt ableiten (blauer Pfeil). Das Ergebnis ist die Richtung des neuen Bewegungsvektors, der dann noch auf die ursprüngliche Länge gebracht werden muss. | + | ''a'' ist der normalisierte Bewegungsvektor, der auf den Intersektionspunkt zeigt, und ''norm'' ist die Normale der Tangente bzw. der Ebene, die sie repräsentiert. Diese Normale lässt sich schnell aus dem Mittelpunkt des Kreises und dem Intersektionspunkt ableiten (blauer Pfeil). Das Ergebnis ist die Richtung des neuen Bewegungsvektors, der dann noch auf die ursprüngliche Länge gebracht werden muss. |
Für den Fall, dass einer der beiden Parameter in nicht-normalisierter Form übergeben werden soll, lässt sich das in der Funktion nachholen. Dazu dienen die beiden auskommentierten Zeilen. | Für den Fall, dass einer der beiden Parameter in nicht-normalisierter Form übergeben werden soll, lässt sich das in der Funktion nachholen. Dazu dienen die beiden auskommentierten Zeilen. | ||
| Zeile 257: | Zeile 257: | ||
<br> | <br> | ||
| − | Viel | + | Viel Spaß beim Experimentieren mit Kollisionen. |
'''Reinhard''' | '''Reinhard''' | ||
| − | {{TUTORIAL_NAVIGATION|[[Tutorial Separating Axis Theorem]]| | + | {{TUTORIAL_NAVIGATION|[[Tutorial Separating Axis Theorem]]|[[Tutorial Kollision2]]}} |
[[Kategorie:Tutorial|Kollision1]] | [[Kategorie:Tutorial|Kollision1]] | ||
Aktuelle Version vom 12. Oktober 2013, 23:38 Uhr
Inhaltsverzeichnis
Überall anstoßen - Kollisionen im 3D-Programm
Wie es zu diesem Tutorial kam
Wahrscheinlich würde es dieses Tutorial nicht geben, wenn da nicht Tuxracer mit seiner miserablen Kollisionsbehandlung wäre. Irgendwie fühle ich mich diesem Programm verpflichtet, und irgendwie landete ich im Forum von Extreme Tuxracer, einem Nachfolger der bekannten Open-Source-Version. Ein paar gut gemeinte Ratschläge von mir, und im Gegenzug war man der Meinung, ich könnte mich wohl um eine vernünftige Kollisionsbehandlung und ordentliche Objekte kümmern.
Dermaßen unter Zugzwang gesetzt, kümmerte ich mich also und betrat damit völliges Neuland. Ich stellte Tuxracer in die Ecke, baute eine Testumgebung auf und befasste mich mit der Berechnung von Schnittpunkten und ähnlichen erquicklichen Dingen. Zugegeben, manchmal hakte es ganz schön, und die vielen Vektoren, die durch meinen Kopf schwirrten, verfolgten mich gelegentlich im Traum und durchbohrten mich wie spitze Pfeile. Irgendwie erreichte ich das gesteckte Ziel. Ob der Code demnächst mal in Tuxracer einfließen wird, kann ich zur Zeit noch nicht genau sagen. Ich weiß ja nicht, was die Jungs noch alles vorhaben, und Programmierer sind oft eigenwillige Menschen.
Auf jeden Fall aber bietet sich nun die Gelegenheit, mich ein wenig für die Hilfe, die ich von der DGL-Community erfahren habe, zu revanchieren. So präsentiere ich hier mein erstes Tutorial, das aus zwei Teilen bestehen wird:
- Der Teil, den du hier liest. Eine einfache und allgemeine Einführung: Was ist das überhaupt, so eine Kollision? Klar, dass sich dieser Teil an Leser richtet, die ganz neu einsteigen wollen. Für den praktischen Einstieg gibt es erste Beispiele zu Strahl-Ebenen-Schnitten und zu Kollisionen von Kugeln mit Ebenen bzw. kreisförmigen Hindernissen.
- Der zweite Teil wird sich mit Kollisionen von Kugeln an dreieckigen Primitiven (erweiterbar auf mehreckige Polygone) befassen. Das ist die vielleicht wichtigste Form der Kollision überhaupt. Ich werde hauptsächlich auf die geometrischen Dinge eingehen.
Voraussetzungen für Teil 1
Was musst du als Leser mitbringen? Eigentlich nicht viel, ein paar OpenGL-Kenntnisse und das Wichtigste über Vektoren. Was unter einem Skalarprodukt zu verstehen ist oder wozu eine Normale gut ist, solltest du schon wissen; auf diese Dinge werde ich nicht näher eingehen. Sollte es hier und da noch etwas hapern, muss ich dich auf andere Tutorials verweisen. Was Kollisionen betrifft, sind keinerlei Voraussetzungen erforderlich. Wer schon etwas darüber weiß, wird wahrscheinlich mit diesem ersten Teil nicht allzu viel anfangen können.
Ein paar Anmerkungen zu Physik-Engines:
Wir müssen uns in diesem Zusammenhang auch die Frage stellen, ob es nicht besser ist, auf eine Physik-Engine wie ODE mit eingebauter Kollisionsbehandlung zurückzugreifen. Zweifellos bietet solch eine Engine manchen Vorteil, vor allem, wenn es um kompliziertere Fälle geht. Dennoch gibt es nach meiner Auffassung gute Gründe, sich selber mit der Programmierung von Kollisionen auseinanderzusetzen.
- So eine Engine ist universell ausgelegt, das heißt, sie ist selten auf die Situation, mit der man es zu tun hat, zugeschnitten. Sie kann meistens mehr als man braucht, macht aber das, was man wirklich braucht, nicht unbedingt optiomal.
- Sich in eine solche Engine einzuarbeiten, geht nicht immer ruck-zuck. Ich weiß nicht, wie es anderen ergeht, aber ich tu mich mit solchen Libraries mitunter recht schwer.
- Selbst wenn man eine Engine benutzt, kann es nicht schaden, wenn man sie nicht blind einsetzt, sondern die Vorgänge etwas versteht.
Was ist eine Kollision?
Die virtuelle Welt wimmelt von Kollisionen, oft an Stellen, wo wir es auf den ersten Blick gar nicht vermuten. Eine Kollision tritt immer dann auf, wenn ein bewegtes Objekt ein anderes bewegtes oder feststehendes Objekt berührt. In den meisten Fällen wird das Programm darauf reagieren, wobei diese Reaktion sehr unterschiedlich sein kann. So ist z.B. denkbar, dass ein Objekt verschwindet, weil es "verschluckt", "eingefangen" oder in irgendeiner Weise zerstört wird. Solche Vorgänge werden oft mit entsprechenden Kollisionsgeräuschen oder Animationen (z.B. Explosionsdarstellungen) verbunden. Es gibt ganz fiese Arten, eine Kollision sichtbar zu machen, aber da meine Gedanken frei sind, muss ich mir das nicht so genau vorstellen - geschweige denn am Bildschirm angucken.
Mindestens ebenso häufig kommt es vor, dass bewegte Objekte durch die Kollision eine Bewegungsänderung erfahren, das heißt eine andere Richtung oder Geschwindigkeit erhalten bzw. sich um die eigenen Achsen drehen. Oft tritt alles gleichzeitig ein, und es ist einzusehen, dass es bei diesen Dingen die physikalische Zusammenhänge eine Rolle spielen. In besonderen Fällen kann sich eine Kollision sogar auf Teile des Objektes auswirken, das dadurch eine andere Gestalt oder "Körperhaltung" erhält. All dieses fasst man üblicherweise unter dem Begriff der Kollisionsverarbeitung (collision response) zusammen.
Doch bevor auf eine Kollision reagiert wird, muss sie erst mal erkannt werden. Die Kollisionserkennung (collision detection) kann mitunter recht aufwendig sein, denn dazu müssen die Berührungspunkte berechnet werden - in erster Linie eine geometrische Aufgabenstellung. Aber da wir nicht die ersten sind, die sich mit solchen Dingen befassen, gibt es eine Reihe von bewährten Funktionen, mit denen diese Aufgaben gelöst werden können.
Bei der Kollisionserkennung kommt noch etwas hinzu: Meistens sind es sehr, sehr viele Dinge, Flächen usw., die möglicherweise im Wege stehen können. Dieses "möglicherweise" ist ernst zu nehmen. Würden wir grundsätzlich alle Objekte in Betracht ziehen, hätten wir es u.U. mit hunderttausenden von Kollisionsprüfungen in jedem Zeittakt zu tun, was verständlicherweise viel kostbare Zeit in Anspruch nimmt. Um den Vorgang zu optimieren, blenden wir von vornherein alle Objekte aus, die aufgrund ihrer Lage keine Kollision verursachen können. Da sind kluge Algorithmen gefragt, und wir setzen uns mit "bounding volumes" und ähnlichen Dingen auseinander. Später etwas mehr davon.
Kollisionen, etwas genauer betrachtet
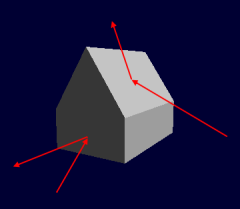
Kollision ist nicht gleich Kollision. Es gibt viele verschiedene Situationen, die sich sowohl in der Methode der Kollisionserkennung als auch in der Kollisionsverarbeitung unterscheiden. Dazu einige Beispiele, zunächst so etwas wie den "Normalfall". Ein Junge spielt mit einem Gummiball, den er fortwährend gegen die Hauswand schießt. Wer kennt nicht dieses nervtötende Rumsen, das unvermeidliche Kollisionsgeräusch, das dabei entsteht? Nun springt der Ball in Nachbars Garten. Der freundliche Nachbar will zeigen, dass er auch noch was in den Beinen hat, und schießt den Ball zurück. Der Schuss gerät zu hoch, der Ball prallt auf das Hausdach ...
Die Abbildung zeigt, dass der Ball nicht mit dem Haus als Ganzes kollidiert, sondern mit den Flächen, die das Haus umschließen. Dabei spielt die Richtung der Fläche eine erhebliche Rolle.
Wenn wir also ein Objekt auf mögliche Kollisionen überprüfen, dann muss das mit allen Flächen geschehen, die das Objekt bilden. Es leuchtet ein, dass dieser Vorgang mitunter sehr komplex werden kann, denn in den seltensten Fällen ist ein Objekt so einfach gestrickt wie das Haus. Dutzende von Flächen sind eher die Regel.
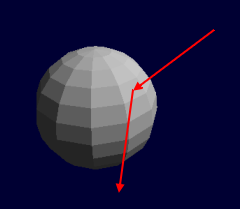
Doch nicht immer haben wir den "Normalfall". Es gibt Situationen, wo wir den Vorgang vereinfachen können. Das können wir an einer Kugel beobachten.
Die abgebildete Kugel besteht aus 144 Flächen, die alle eine andere Ausrichtung haben. Natürlich könnten wir "normal" vorgehen und alle Flächen auf Kollision testen. Die Frage ist jedoch, wozu das gut sein soll, denn das Auge nimmt überhaupt nicht wahr, an welcher Fläche genau die Kollision stattfindet. Die Flächen in ihrer Gesamtheit werden vielmehr als Kugel wahrgenommen ...
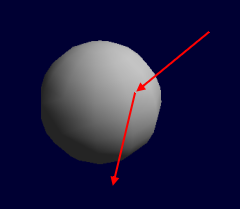
... und dann können wir auch gleich hingehen und die Kollision so berechnen, als hätten wir eine ideale Kugel vor uns, mit einer einzigen, kugelförmigen Fläche. Das geht wesentlich einfacher und schneller, als wenn wir uns alle Teilflächen vornähmen. Bei der dargestellen Kugel handelt es sich übrigens um dieselbe wie im Bild davor, nur wurde sie diesmal mit aktiviertem Smooth-Shading unter Verwendung der Vertexnormalen gezeichnet.
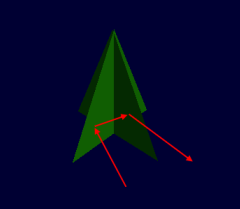
Nicht ganz unproblematisch ist die Kollision an Objekten, die stark vereinfacht gezeichnet werden. Wenn z.B. sehr viele Bäume zu zeichen sind, werden sie oft nur als Textur dargestellt, und zwar kreuzweise, damit der Eindruck eines 3-dimensionalen Objektes entsteht. Das Verfahren ist praktisch und schnell, hat aber deutliche Schwächen, wenn wir die Objekte aus der Nähe betrachten.
So ähnlich können Nadelbäume dargestellt werden, auf die Textur habe ich hier verzichtet. Als Kinder haben wir mit solchen Dingern aus Karton unseren Playmobil-Zoo begrünt, also auch in der konkreten Welt sind solche Gebilde praktisch. Eine Kollsion könnte zwar genau berechnet werden, wäre aber völlig unrealistisch, denn der Baum würde wie ein Fangkäfig wirken und die Kugel zurückweisen.
Wenn diese Art von Objekten überhaupt "kollisionsfähig" gemacht werden sollen, dann geht das nur, indem wir einen unsichtbaren, virtuellen Körper darum spannen, die Kollision daran vornehmen und hoffen, dass der Anwender nicht allzu kritisch ist.
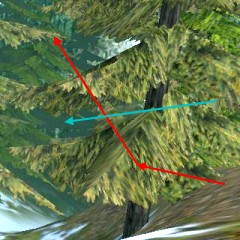
Bleiben wir noch etwas bei den Bäumen. Der ideale Baum ist so gestaltet, dass er einfache, kollisionsfähige Flächen aufweist, andererseits aber doch einen guten Gesamteindruck macht. Hier ein Screenshot aus dem Programm Tuxracer 1.1:
Der blaue Pfeil deutet an, dass hier der Baum ohne Kollision durchquert werden kann, während der rote Pfeil eine mögliche Kollision beschreibt.
Die Situation sieht wieder ganz anders aus, wenn der Baum relativ klein gegenüber dem bewegten Objekt ist. Dann gibt es trotz Lücken kein Durchkommen, und auch der Aufprall auf einem "Blätterdach" lässt sich kaum noch vernünftig umsetzen. Ein Beispiel, das die Situation noch deutlicher macht:
Was soll denn nun geschehen, wenn ein Ball in dieses Blättergewirr fliegt? Kollisionen an den einzelnen Blättern? Das wäre nicht nur programmtechnisch unzumutbar, sondern zudem völlig unrealistisch. Ein einzelnes Blatt oder ein dünner Zweig stellt für den Ball keinen nennenswerten Widerstand dar, wohl aber die Baumkrone als Ganzes, mit dem Gewirr von Blättern und Zweigen. In solchen Fällen hilft uns die Realität weiter. Der Ball würde irgendwo in der Baumkrone zum Stoppen kommen und dann herunterfallen. Sowas wie eine weiche Kollision, die sich mit etwas Einfallsreichtum durchaus simulieren lässt.
Dann gibt es ja noch den Winter mit kahlen Baumkronen:
Wahrscheinlich wird der Ball gelegentlich "hängen bleiben", aber ebenso könnte er irgendwo aufprallen, seine Richtung ändern und mit verminderter Geschwindkeit weiter fliegen. Wo er aufprallt, ist kaum auszumachen und wahrzunehmen. Da könnten wir ein wenig mit dem Zufall arbeiten, die Richtung etwas ändern, die Geschwindigkeit herabsetzen usw.
Nun ist die Sache mit den Bäumen ja klar; das sind Objekte, die aufs Gelände gesetzt werden und deshalb im Wege stehen können. Es gibt aber noch etwas anderes, was im Weg ist, nämlich der Weg selbst. Verrückt? Nicht, wenn wir daran denken, was ich weiter oben angemerkt habe, nämlich dass jede Berührung, die irgendwie den Lauf unseres Objektes beeinflusst, eine Kollision ist. Ohne eine Kollsision mit dem Weg oder - programmtechnisch ausgedrückt - mit den Polygonen würde unser Objekt wie ein Taucher unter der Erdoberfläche oder dem Fussboden verschwinden. Und wir Beobachter, die wir dem Objekt mit der Kamera folgen, gleich mit.
Heißt das nun, dass wir im Grunde gar nicht zwischen dem natürlichen Untergrund und den aufgesetzten Objekten unterscheiden? Im Prinzip läuft es tatsächlich darauf hinaus, denn auch der Untergrund ist nichts anderes als ein ausgedehntes Objekt, bestehend aus vielen Dreiecken (ich setze mal voraus, dass wir nicht zu den Experten gehören, die die Landschaft aus Bezierflächen und ähnlichen Gebilden der höheren Mathematik bilden). Der Unterschied zwischen dem natürlichen Surface und den anderen Objekten besteht eigentlich nur darin, dass wir die Daten an verschiedenen Stellen im Programm speichern.
Werfen wir noch einmal einen Blick in das Programm Tuxracer:
Hier liegt der Pinguin vor einer Brücke, über die er hinübergleiten soll. Ohne Brücke würde er dem Terrain folgen und ins Tal rutschen. Notgedrungen müssten wir ihm folgen und auf der anderen Seite motivieren, wieder hinaufzuklettern. Mühsam, deshalb haben wir ihm ja eine Brücke gebaut, eine sehr nützliche Kollision, wie wir sehen. Und wenn wir außerdem erkennen, dass es egal ist, ob der antarktische Vogel über natürliches Terrain oder eine künstliche Brücke gleitet, haben wir so ziemlich erfasst, wass eine Kollision im 3D-Programm ist.
Wir bauen einen Billardtisch ...
Ursprünglich wollte ich an dieser Stelle noch einen wichtigen Gedanken zur Kollision zum Besten geben, aber ich höre schon die Mahnung des Lektors: "Die Leute wollen nicht nur lesen, die wollen was ausprobieren." Stimmt absolut, deshalb bringe ich zuerst einige Vorschläge zu Experimenten mit ganz einfachen Kollisionen, die aber trotz der Einfachheit - hoffe ich jedenfalls - etwas lehrreich sind. Den wichtigen Gedanken kann ich anschließend noch anbringen.
Nun ja, wie die Überschrift schon sagt, geht es um die Kugel auf dem Billardtisch. Das ist eine fast klinisch reine Situation für Kollisionen nach dem Motto Einfallswinkel = Ausfallswinkel. Außerdem können wir die Sache zweidimensional untersuchen, obwohl die Szenerie dreidimensional gestaltet ist.
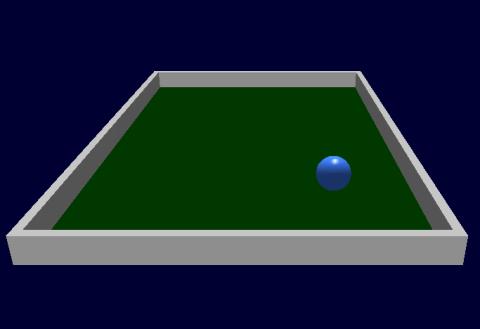
Um mit der Billardkugel herumspielen und herumrechnen zu können, brauchen wir erst mal eine geeignete Testumgebung. Die will ich aber bewusst nicht in allen Einzelheiten beschreiben, etwas musst du als Leser selbst dazu beitragen. Du kannst ein Delphi-Template von DGL benutzen, oder du verwendest ein C-Programmgerüst mit SDL, ähnlich wie ich es auf meiner Webseite beschrieben habe. Letzteres bietet sich an, wenn du Linux bevorzugst (ich gehöre dazu). Du kannst natürlich auch eines der ersten Nehe-Tutorials nehmen, die für alle denkbaren Plattformen und Programmiersprachen zur Verfügung stehen. Die Szenerie, also der Billardtisch, ist recht schlicht aufgebaut und lässt sich schnell programmieren. Ich denke, auch diese Aufgabe kannst du selber lösen. Am Schluss könnte es etwa so aussehen:
Die Kugel wird am einfachsten mit gluSphere erzeugt. Nicht vergessen, in Beleuchtung und Material das Specular-Licht richtig einzustellen, sonst erscheint die Kugel wie eine tote Scheibe. Die Umgebung kann auch ohne Beleuchtung gezeichnet werden. Nun ja, und dann solltest du noch eine verstellbare Kamera einbauen. Es kann ganz nützlich sein, wenn der Blickwinkel geändert wird, besonders der Blick von oben zeigt einiges genauer.
... und lassen die Kugel rollen
Ich denke, das ist nun der richtige Zeitpunkt, ein wenig über die Bewegung von Objekten in 3D-Programmen nachzudenken. Grundsätzlich gibt es keine echte Bewegung, sondern es wird nur Bewegung vorgetäuscht, indem Objekte schnell genug an verschiedenen Stellen gezeichnet werden. Dieses "schnell genug" wird durch die Trägheit des Auges bestimmt; das Auge verschmilzt Abläufe, die schneller als etwa 20 mal pro Sekunde präsentiert werden, zu einem flüssig erscheinenden Vorgang. Ich will nicht weiter darauf eingehen, denn die Zusammenhänge dürften von Film und Fernsehen her bekannt sein.
Jedenfalls ist es in 3D-Programmmen nicht anders. Dort spricht man von Frames und misst die Schnelligkeit der Bildfolge in fps (frames per second). In jedem Frame zeichnen wir das bewegte Objekt an einer anderen Stelle. Damit dürften wir bereits erkennen, dass es vor allem um die Berechnung der "richtigen" Stelle geht, wenn die Bewegung als flüssig und realistisch wahrgenommen werden soll.
Dazu betrachten wir wieder unseren Billardtisch und nehmen an, dass die Kugel sich mit konstanter Geschwindigkeit in gleicher Richtung fortbewegen soll. Mögliche Kollisionen lassen wir noch außer acht.
Um die Bewegung zu kontrollieren, müssen wir in jedem Frame zwei Dinge festhalten. Da ist zum einen die Position, an dem die Kugel gezeichnet wurde, zum anderen die Geschwindigkeit, die sie beim Erreichen dieser Position hat. Die Position ist, geometrisch gesehen, ein Punkt und wird durch seine drei Koordinaten x, y und z beschrieben. Auch die Geschwindigkeit benötigt diese 3 Komponenten, dann dabei handelt es sich um einen Vektor. In der realen Welt meinen wir mit Geschwindigkeit zwar meistens nur den skalaren Wert (z.B.80 km/h), doch in 3D-Programmen müssen wir die Geschwindigkeit voll erfassen, d.h. die Richtung mit einbeziehen. In diesem Zusammenhang noch eine kurze begriffliche Klärung: Wenn ich im folgenden nur den skalaren Anteil meine, werde ich zur Unterscheidung den Ausdruck Geschwindigkeitsbetrag verwenden. In Programmen, wo meisten englische Bezeichner verwendet werden, wird oft eine ähnliche Unterscheidung getroffen: Geht es um die Geschwindigkeit (mit Richtung), dann finden wir häufig den Ausdruck velocity; geht es nur um den (skalaren) Betrag, dann wird der Begriff speed bevorzugt.
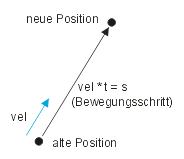
Aber zurück zur Kugel. Wir befinden uns nun im nächsten Frame und müssen die Kugel an der neuen Position zeichnen. Nun sollte wohl eines klar sein: Wenn wir einen Punkt verschieben wollen, dann erreichen wir das, indem wir einen Vektor addieren. Nur kann ich nicht ohne weiteres eine Geschwindigkeit zu einer räumlichen Position addieren, das sind verschiedene Dinge. Aber es kommt ja die Zeit hinzu, die seit dem letzten Frame vergangen ist. Je mehr Zeit vergangen ist, desto größer ist der Bewegungsschritt. Folglich muss ich den Geschwindigkeitsvektor mit der Zeitspanne multiplizieren (evtl. noch zusätzlich skalieren), und nach dem Gesetz v * t = s wird aus dem Geschwindigkeitsvektor ein Wegvektor, den ich im folgenden Bewegungsvektor nenne. Den addieren wir zur alten Position und wissen, wo die Kugel nun gezeichnet werden muss. Die neue Position halten wir nun wieder für den nächsten Frame fest. Die Geschwindigkeit hatten wir ja als konstant vorausgesetzt und muss nicht aktualisiert werden.
Noch einmal kurz zur Zeitspanne zwischen zwei Frames. Zwar wird diese auf ein- und demselben Rechner meistens nicht allzusehr schwanken, aber es gibt immer wieder Dinge, die von Frame zu Frame unterschiedlich sind. Außerdem schlägt natürlich die Rechnergeschwindigkeit voll durch. Um Konstanz zu erzeugen und die Bewegung flüssig erscheinen zu lassen, sollten wir unbedingt die realen Zeitspannen berücksichtigen und nicht versuchen, die Geschwindigkeit durch irgendeine Konstante auf das richtige Maß zu quetschen. Zu dieser Problematik gibt es einen aufschlussreichen Artikel im DGL-Wiki: "Timebased Movement".
Wir brauchen also zwei Vektor-Variablen, die wir nach dem Programmstart auf geeignete Anfangswerte setzen:
TVector position;
TVector velocity;
position.x = 0.0 // richtet sich nach dem Billardkasten
position.y = 0.5 // entspricht dem Radius der Kugel, bleibt konstant
position.z = 0.0 // richtet sich nach dem Billardkasten
velocity.x = 0.1 // etwas nach rechts bewegen
velocity.y = 0.0 // bleibt immer 0, zweidimensional
velocity.z = -0.5 // Vorwärtsbewegung
Die Werte müssen wir natürlich anpassen. Vor dem Zeichnen der Kugel wird in jedem Frame die Position aktualisiert:
position = AddVectors (position, ScaleVector (timestep, velocity));
Wenn wir das Programm starten, rollt die Kugel, lässt sich aber von der Bande nicht aufhalten und verschwindet in der unendlichen Weite. Vielleicht wird sie irgendwann den Mars umkreisen oder in der Sonne verglühen, wobei wir dafür erst den passenden Code schreiben müssten. ;)
Nun zur Kollision
... und damit zum Kern dieser einfachen Kollisionsexperimente. Die Kollisionserkennung besteht darin, dass wir feststellen, ob und wo die Kugel die Bande berührt, so dass wir sie dann im richtigen Winkel in den Innenraum zurückschicken können. Das wäre die Kollisionsverarbeitung. Dass jeder Aufprall und auch das Rollen auf dem grünen Tuch mit Energieverlust verbunden ist, übersehen wir mal großzügig. Das ist das Schöne an der virtuellen Welt, wir können sie nach unseren Vorstellungen gestalten und Naturgesetze einfach ignorieren.
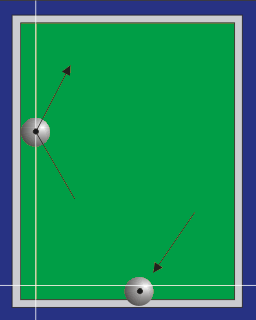
Ein Problem ist die Abmessung der Kugel. Wenn wir die Position angeben, dann meinen wir natürlich den Mittelpunkt, alles andere wäre unsinnig. Nun berührt der Mittelpunkt aber niemals die Bande, doch zum Glück können wir diesen Umstand recht einfach umgehen. Später, bei "richtigen" Kollisionen, werden sich daraus allerdings einige Probleme ergeben. Schauen wir zunächst die Abbildung an:
Links sehen wir die Kugel, wie sie gerade die Bande berührt. Wir erkennen auch, wie der Weg weitergehen soll. Die weiße Linie grenzt den Bereich ein, in dem der Mittelpunkt sich bewegen kann. Das heißt, wir brauchen den "bekugelbaren" Innenraum nur um den Radius der Kugel zu verkleinern. Immer, wenn z.B. die x-Position der Kugel sich auf der linken, weißen Linie befindet, berührt die Kugel die Bande; ist die x-Position kleiner als die Linie, taucht sie bereits in die Bande ein (in der virtuellen Welt geht das). Das wäre bei der unteren Kugel der Fall, nur dass es hier um die z-Position geht.
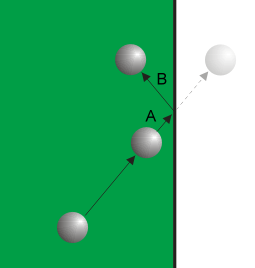
Was ist zu tun? Genauer: Wo müssen wir die Kugel abfangen und ihr mitteilen, dass es beim nächsten Mal in anderer Richtung weitergeht? Wir können das erledigen, nachdem die Kugel die Grenzlinie überschritten hat, oder wir machen das vorher, indem wir den anstehenden Bewegungsschritt nur probehalber durchführen und ggfs. unterlassen? Beides ist nicht ganz sauber, und nur, wenn die Kugel sehr langsam rollt und die Bewegungsschritte entsprechend klein sind, fällt es nicht auf. Wenn wir genau sein wollen, müssen wir ein wenig weiter ausholen und den Berührungspunkt auf der weißen Linie finden. Nennen wir ihn Intersektionspunkt, obwohl der eigentliche Intersektionspunkt direkt an der Bande liegt.
Damit sind wir schon mitten drin im Kollisionszirkel. Es geht darum, den Schnittpunkt eines Strahls mit einer Ebene zu berechnen (ray-plane intersection). Der Strahl ist nichts anderes als der Bewegungsvektor der Kugel, der von der Kugelposition wegzeigt. Und die Ebene müssen wir uns senkrecht auf der weißen Linie vorstellen, wie eine unsichtbare Wand.
Die mathematischen Hintergründe wollen wir uns ersparen, hier die Funktion, die den Intersektionspunkt ausrechnet:
double PlaneIntersect (TVector pOrigin, TVector pNormal, TVector sPosition, TVector sDir)
{
double d = -(DotProduct (pNormal, pOrigin));
double num = DotProduct (pNormal, sPosition) + d;
double denom = DotProduct (pNormal, sDir);
return -(num / denom);
}
pOrigin ist irgendein Punkt auf der Ebene und damit auf der weißen Hilfslinie. Es dürfte kein Problem sein, irgendeinen geeigneten Punkt zu finden. pNormal ist die Normale der Ebene, ein Vektor, den wir ganz einfach im Kopf ausrechnen können. Nehmen wir dazu die linke Begrenzungsebene. Aus der Sicht der Kugel zeigt die Normale nach rechts, also ist der Vektor (1, 0, 0). Ähnliches gilt für die anderen drei Ebenen.
sPosition ist der Positionspunkt der Kugel, und sDir ist der Bewegungsvektor. Das Ergebnis gibt den Abstand von sPosition zur Ebene an, und zwar als Faktor, mit dem wir den Bewegungsvektor multiplizieren müssen, wobei es egal ist, ob der Vektor normalisiert ist oder nicht. Ist das Ergebnis negativ oder größer als der Bewegungsschritt, wird die Bande nicht erreicht und wir bewegen die Kugel ganz normal vorwärts. Andernfalls verkürzen wir den Schritt, so dass die Kugel direkt an der Bande zu liegen kommt.
Nun könnten wir auf den Gedanken kommen, es ganz perfekt machen zu wollen und im selben Frame einen zweiten Teilschritt in der neuen Richtung anzuschließen, so dass sich ein vollständiger Bewegungsschritt ergibt. Vom Bewegungsablauf her wäre das korrekt, doch es kommt ein anderer Aspekt hinzu. Wir würden nur selten die Kugel unmittelbar an der Bande sehen, und wir bekämen den Eindruck, als hätte sie Berührungsängste. Tatsächlich dürfen wir den optischen Eindruck nicht außer Acht lassen. Wenn die Kugel dagegen mal einen zu kurzen Bewegungsschritt macht, fällt es wegen der plötzlichen Richtungsänderung nicht auf. Du kannst es ja ausprobieren.
An der Bande lassen wir die Kugel zunächst liegen, versäumen aber nicht, die Richtung so zu verändern, dass der Aufprallwinkel gleich dem Rückprallwinkel ist. Auch das ist kein Problem, schauen wir wieder auf die linke Bande. Es ändert sich hier nur die x-Richtung, während die Fortbewegung in z-Richtung gleich bleibt. Also stülpen wir den x-Wert des Bewegungsvektors um:
velocity.x = - velocity.x;
Mit den anderen Banden verfahren wir analog. Es ist aber wichtig, dass wir immer alle vier Banden überprüfen. Es kann nämlich sein, dass die Kugel auf eine Ecke zusteuert und gleichzeitig mit zwei Banden in Konflikt gerät. Dann müssen in ein- und demselben Frame zwei Richtungen umgedreht werden. Wenn wir feststellen, dass die Kugel gelegentlich außerhalb des Käfigs hin- und herzittert und nicht wieder hinein will, haben wir diesen Punkt nicht beachtet.
Geht noch mehr?
Oh ja, wir können noch wesentlich mehr mit dem Billardtisch anfangen, aber dazu will ich nur einige Tipps geben. Wenn das Bisherige verstanden ist, dürfte die Umsetzung keine großen Probleme mehr machen.
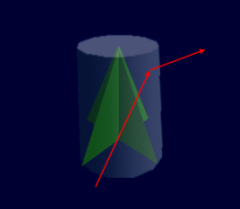
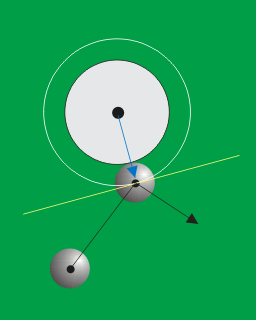
Eigentlich war die Bewegung der Kugel bis jetzt langweilig, immer dieselben Bahnen und Winkel, kreuz und quer. Wir können es zwar einrichten, dass wir per Tastendruck die Richtung der Kugel verstellen, aber so richtig interessant ist auch das nicht. Besser ist es, ein Hindernis einzubauen, das nicht so berechenbar ist. Dazu nehmen wir einen Zylinder oder eine zweite Kugel, die wir fest irgendwo im Innern des Billardtisches positionieren. Mit diesem runden Gebilde soll die bewegliche Kugel nun kollidieren - wenn sie zufällig getroffen wird. Schauen wir uns also an, wie das gemeint ist:
In der Abbildung steckt alles, was wir zur Lösung des Problems brauchen. Wieder haben wir die weiße Linie, die uns erlaubt, mit dem Mittelpunkt der Kugel zu rechnen, und natürlich ist der äußere Kreis um den Radius der Kugel größer als der eigentliche Kollisionskörper. Wir sehen die gelb eingezeichnete Tangente, an der wir die Reflexion vornehmen. Doch vorher müssen wir wieder den Intersektionspunkt haben, worauf der blaue Pfeil zeigt. Hier nun die Funktion, die uns den Punkt liefert:
double CircleIntersect (TVector center, double radius,
TVector sPosition, TVector sDir)
{
center.y = sPosition.y = sDir.y = 0;
TVector q = SubtractVectors (center, sPosition);
double c = VectorLength (q);
double v = DotProduct (q, sDir);
double d = radius * radius - (c * c - v * v);
if (d < 0.0) return -1;
return v - sqrt (d);
}
Die ersten beiden Parameter beschreiben den Kollisionskreis (oder Zylinder) und dürften selbsterklärend sein; die beiden anderen Parameter sind dieselben wie bei der Funktion weiter oben. Auch das Ergebnis wird in gleicher Weise verwendet. Halt, eines ist zu beachten: sDir muss nun auf jeden Fall normalisiert sein!
Schauen wir genauer hin, dann entdecken wir darin eine quadratische Gleichung. Nun hat eine quadratische Gleichung mitunter zwei Lösungen, und das ist auch erklärlich, denn der Strahl schneidet den Kreis meistens an zwei Stellen. Die Funktion liefert aber nur den Eintrittspunkt des Strahls zurück, denn der hintere Schnittpunkt ist uninteressant. Wird der Kreis nicht geschnitten, ist das Ergebnis -1. Übrigens ist die Funktion eigentlich für eine Kugel ausgelegt. Sie kann aber auch zweidimensional für einen Kreis oder Zylinder benutzt werden, indem die y-Komponenten auf 0 gesetzt werden (1. Zeile).
Der Reflexionswinkel lässt sich leider nicht mehr ganz so einfach berechnen wie bei der Kollision an der Bande. Die Tangente ist ja nicht nach x oder z ausgerichtet, sondern kann irgendwie liegen. Aber auch hierfür gibt es eine praktische Funktion:
TVector ReflectVector (TVector a, TVector norm)
{
TVector res;
// NormalizeVector (&a);
// NormalizeVector (&norm);
double dotprod = DotProduct (a, norm);
res.x = a.x - 2 * norm.x * dotprod;
res.y = a.y - 2 * norm.y * dotprod;
res.z = a.z - 2 * norm.z * dotprod;
return res;
}
a ist der normalisierte Bewegungsvektor, der auf den Intersektionspunkt zeigt, und norm ist die Normale der Tangente bzw. der Ebene, die sie repräsentiert. Diese Normale lässt sich schnell aus dem Mittelpunkt des Kreises und dem Intersektionspunkt ableiten (blauer Pfeil). Das Ergebnis ist die Richtung des neuen Bewegungsvektors, der dann noch auf die ursprüngliche Länge gebracht werden muss.
Für den Fall, dass einer der beiden Parameter in nicht-normalisierter Form übergeben werden soll, lässt sich das in der Funktion nachholen. Dazu dienen die beiden auskommentierten Zeilen.
Wer Spaß am Billardtisch gefunden hat, kann noch eine ganze Menge damit machen. Mit mehreren runden Hindernissen ließe sich z.B. so etwas wie ein Flipperautomat aufbauen. Bei Berührung prallt die Kugel nicht nur ab, sondern erhält einen Geschwindigkeitsimpuls. Wer allerdings vorhat, ein richtiges Billardspiel zu bauen, mit mehreren bewegten Kugeln, muss wesentlich tiefer in die mathematische Kiste greifen. Die andere Kugel hält ja nicht bis zum nächsten Frame still, sondern der Zusammenprall wird in der Regel "zwischen den Zeiten" erfolgen. Diese Zeitpunkte und Kollisionsstellen müssen dann berechnet werden, was häufig auf Verfahren wie die ODE-Solver (von ordinary differential equations) hinausläuft. Nicht zu verwechseln mit der eingangs erwähnten Physik-Engine ODE (open dynamics engine). Gerade bei Aufgabenstellungen wie der Billardtisch dürfte auch das letztgenannte ODE eine gute Hilfe sein.
Wer sich für einfache Zusammenstöße zweier Kugeln interessiert, kann ja mal im Netz unter den Stichwörtern "Stoßgesetze" und "Impulsgesetze" nach Informationen suchen. Eine gute Einstiegsseite ist die von Wikipedia, auf der u.a der Zusammenprall zweier Kugeln in einer Animation veranschaulicht wird:
http://de.wikipedia.org/wiki/Sto%C3%9F_(Physik)
Und, nicht zu vergessen, auch das gute, alte Physikbuch kann hilfreich sein - sofern ihr nach Beendigung der Schulzeit nicht alle Bücher verbrannt habt ;-)
Nun doch noch der wichtige Gedanke
Auf einen Punkt möchte ich noch hinweisen, weil er für eine saubere Kollisionsberechnung von großer Bedeutung ist. Wir haben bei den Versuchen rund um den Billardtisch den Berührungspunkt der Kugel mit der Bande (Intersektionspunkt) quasi aus der Ferne berechnet. Wenn der Punkt so weit weg liegt, dass keine Kollision stattfinden kann, gut, dann lassen wir der Kugel freien Lauf. Voraussetzung für diese sichere Methode ist, dass wir wissen, welcher Punkt der Kugel das Hindernis berührt; dann können wir die Bahn dieses Punktes als Strahl betrachten. Im Falle des Billardtisches gelang es uns deshalb, weil wir die unsichtbaren Linien oder Ebenen definieren konnten, wo der Mittelpunkt der Kugel anstößt. Das funktioniert aber nur in ganz bestimmten Fällen, nämlich bei kreisrunden oder unbegrenzt geraden Hindernissen. Ein viereckiges Hindernis könnten wir mit der Methode nicht auf den Billardtisch stellen, wie das folgende Bild zeigt:
Die Kugel würde an der Kollisionslinie zurückprallen, obwohl sie das Hindernis nur streift und allenfalls ein wenig abgelenkt wird.
Bei unseren Versuchen lernten wir zwei Intersektions-Funktionen kennen. Wenn wir uns im Internet umschauen, dann finden wir eine Vielzahl von solchen Funktionen, es gibt sie für alle möglichen Linien, Flächen und Körper. Doch die weitaus meisten sind für Kollisionsberechnungen nur bedingt brauchbar, denn ihre Ergebnisse stellen uns vor vollendete Tatsachen. Sie geben nämlich an, ob und wo die Objekte sich bereits schneiden, nicht aber, an welchem Punkt genau die wichtige Erstberührung stattfindet.
Manchmal reicht aber die Feststellung, ob sich zwei Objekte schneiden, z.B. bei der Kollisionserkennung mit Hüllkörpern (bounding volumes). Dabei geht es nur darum, in einem ersten Schritt zu ermitteln, ob sich zwei Objekte nahe genug gekommen sind, um eine genauere Kollisionserkennung anzuschließen. Besonders einfach und schnell geht diese "Vorerkennung" mit Kugeln oder Kreisen. Die schneiden sich nämlich, wenn der Abstand der Mittelpunkte kleiner als die Summe der Radien ist, was relativ einfach nachzuvollziehen ist. Allerdings heißt es ein wenig aufpassen, denn bei größeren Geschwindigkeiten kann es passieren, dass ein Objekt übersprungen wird und die Kollisionserkennung fehlschlägt. Genaueres zu diesen Methoden werde ich vielleicht in einem Folge-Tutorial sagen.
So, das war's für dieses Mal. Es ging in diesem Tutorial noch nicht um komplizierte Techniken zur Kollisionsberechnung, sondern es sollte vor allem ein Gespür für Kollisionen und die zu erwartenden Probleme entstehen. Sollte das rübergekommen sein, hat das Tutorial seinen Zweck erreicht. Im nächsten Tutorial geht es dann schon mehr zur Sache, dann werde ich die vielleicht wichtigste Form der Kollision beschreiben, nämlich die an dreieckigen Polygonen und vor allem deren Kanten.
Viel Spaß beim Experimentieren mit Kollisionen.
Reinhard
|
|
||
Vorhergehendes Tutorial: Tutorial Separating Axis Theorem |
Nächstes Tutorial: Tutorial Kollision2 |
|
|
Schreibt was ihr zu diesem Tutorial denkt ins Feedbackforum von DelphiGL.com. Lob, Verbesserungsvorschläge, Hinweise und Tutorialwünsche sind stets willkommen. |
||