Konvex: Unterschied zwischen den Versionen
(→Unterschiede: Definition für konkave Polygone war nicht korrekt) |
(Ergänzung der Definition konvex/konkav) |
||
| Zeile 4: | Zeile 4: | ||
Konvexe und konkave Polygone unterscheiden sich in einem essenziell wichtigen Punkt. Wenn man eine Linie zwischen einem Eckpunkt und dessen übernächsten Nachbarn zieht, liegen bei konvexen Polygonen der übersprungene Eckpunkt immer außerhalb des "neuen" Polygons. Zieht man eine solche Linie für alle Eckpunkte eines Polygons und liegt mindestens ein übersprungener Punkt im "neuen" Polygon, so ist das Polygon konkav. | Konvexe und konkave Polygone unterscheiden sich in einem essenziell wichtigen Punkt. Wenn man eine Linie zwischen einem Eckpunkt und dessen übernächsten Nachbarn zieht, liegen bei konvexen Polygonen der übersprungene Eckpunkt immer außerhalb des "neuen" Polygons. Zieht man eine solche Linie für alle Eckpunkte eines Polygons und liegt mindestens ein übersprungener Punkt im "neuen" Polygon, so ist das Polygon konkav. | ||
| + | Wenn der übersprungene Eckpunkt '''auf''' der neu entstandenen Kante liegt, gilt das Polygone auch dann als konvex. | ||
| − | + | Eine andere einfache Unterscheidungsregel ist die folgende: Betrachtet man an jedem Eckpunkt des Polygons den Innenwinkel, so beträgt dieser bei konvexen Polygonen maximal 180°. Ist auch nur ein Innenwinkel des Polygons größer als 180°, so ist das Polygon konkav. | |
== Skizze == | == Skizze == | ||
Aktuelle Version vom 5. April 2012, 21:16 Uhr
Inhaltsverzeichnis
konvexe und konkave Polygone
Unterschiede
Konvexe und konkave Polygone unterscheiden sich in einem essenziell wichtigen Punkt. Wenn man eine Linie zwischen einem Eckpunkt und dessen übernächsten Nachbarn zieht, liegen bei konvexen Polygonen der übersprungene Eckpunkt immer außerhalb des "neuen" Polygons. Zieht man eine solche Linie für alle Eckpunkte eines Polygons und liegt mindestens ein übersprungener Punkt im "neuen" Polygon, so ist das Polygon konkav. Wenn der übersprungene Eckpunkt auf der neu entstandenen Kante liegt, gilt das Polygone auch dann als konvex.
Eine andere einfache Unterscheidungsregel ist die folgende: Betrachtet man an jedem Eckpunkt des Polygons den Innenwinkel, so beträgt dieser bei konvexen Polygonen maximal 180°. Ist auch nur ein Innenwinkel des Polygons größer als 180°, so ist das Polygon konkav.
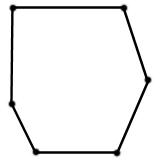
Skizze
Konvex
Konkav
 Der markierte Eckpunkt macht das Polygon konkav. |
 Wird er übersprungen, liegt er im neu entstandenen Polygon. |
Bedeutung
Die Klassifizierung von Polygonen ist z.B. bei der Tesselierung von Bedeutung.
Auch die standard OpenGL Zeichenroutine (basierend auf glBegin) zeichnet ausschließlich konvexe Polygone richtig. Die falsche Darstellung äußert sich meist darin, dass eine zusätzliche Kante vom letzten Punkt zum ersten Punkt des Polygons gezogen wird.
