Version vom 18. November 2005, 21:20 Uhr

Von Teekannen und Bäumen oder PATHFINDING

Einleitung

Hallo und willkommen zu meiner - etwas anderen – Methode eine Wegfinderoutine (Ich liebe dieses Wort... :) zu basteln. Ich sage hier bewusst basteln, weil es evtl. effektivere Systeme gibt. Doch seht selbst...

Was ist an dieser Methode so anders?

Flo hat hier auf DGL bereits eine Möglichkeit aufgezeigt, Pathfinding zu verwenden. Doch erlaubt dieses System "nur" 8 verschiedene Richtungen, in welche die Einheiten sich bewegen können. Dieses oder ähnliche Systeme findet man häufig in 2D Strategiespielen, wo sich die Einheiten ja auch nur in eine bestimmte Anzahl Richtungen drehen können.

Dieses System jedoch hat diese Beschränkung nicht. Einheiten können in alle Richtungen bewegt werden und dadurch wird die Strecke, welche die Einheiten zurücklegen müssen auf ein Minimum reduziert. Dieses (oder ein ähnliches System) kommt bei den meisten 3D Strategiespielen vor, wo sich die Einheiten ja bekanntlich frei drehen können. Doch dieses System erfordert mehr Aufwand. Auch von Mathe bleibt man nicht verschont. Allerdings hält sich der Aufwand in Grenzen und erfreut am Ende dann umso mehr, wenn alles klappt. Ebenso wie die von Flo verwendete Methode, benötigt auch dieses System ein Spielfeld, welches sich aus Quadraten zusammensetzt.

Ein kleines Beispiel

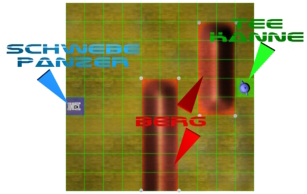
Ihr habt euch vielleicht schon gefragt, was der Titel des Tutorials bedeutet. Nun, es sei euch hiermit verraten. Um die Technik etwas anschaulicher zu gestalten, soll das System anhand eines einfachen Beispiels erläutert werden. In diesem Beispiel soll eine Teekanne auf einem grünen Feld das Ziel darstellen und das blaue Feld ist der Startpunkt einer Einheit, die zu dem grünen Feld gelangen möchte.

Wie man auf dieser Übersichtskarte erkennen kann, befinden sich Hindernisse (Berge) zwischen dem Startpunkt und dem Zielpunkt.

Die Technik dahinter

Soweit, so gut. Doch woher weiß die Einheit auf dem Startfeld nun, wie sie zur Teekanne kommt? Wir brauchen einen Algorithmus, der den kürzesten Weg vom Startpunkt zur Teekanne ermittelt und dabei noch einigermaßen schnell ist. Wenn man sich überlegt, welchen Weg man selbst in diesem Beispiel wählen würde, kommt man auf folgende Kriterien, die dieser Weg erfüllt:

• Der Weg ist gültig, ist also begehbar
• Der Weg geht um die Hindernisse herum
• Es ist der kürzeste Weg

Für den Fall, dass keine direkte Verbindung vom Startpunkt zum Ziel, wie in diesem Beispiel, möglich ist, muss also ein Weg um die Hindernisse herum gefunden werden. Dieser Weg muss die oben genannten Kriterien erfüllen. Somit steht fest, was unser Algorithmus können muss:

• Selbstständiges Erkennen der Hindernisse
• Berechnen der Kanten der Hindernisse
• Feststellung der Eckpunkte der Hindernisse
• Ermittlung des kürzesten Weges anhand dieser Daten

Die Ecken der Hindernisse lassen sich leicht ermitteln, da die ganze Karte ja in gleichgroße Quadrate unterteilt ist. Die Kanten der Hindernisse werden auf ähnliche Art und Weise berechnet. Diese Kanten verlaufen ja bekanntlich zwischen den Eckpunkten, die wir schon ermittelt haben.

Die Berechnung der Ecken und Kanten macht man wohl am Besten beim Laden des Levels oder beim Speichern im Leveleditor. Wenn sich an der Karte im Spielverlauf etwas ändert – sei es durch gefällte Bäume oder zerstörte Mauern – müssen diese Daten natürlich erneut berechnet werden.

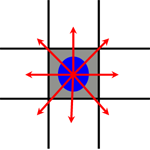
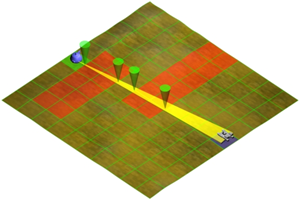
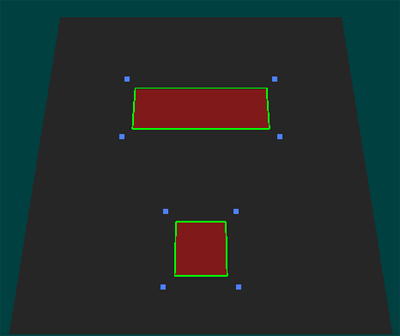
Vereinfachen wir die Situation zunächst etwas: Angenommen, es gäbe auf der Karte keine Hindernisse, so könnte die Einheit geradewegs zur Teekanne steuern. (Auf der Abbildung sind die ehemaligen Hindernisse rot dargestellt und die Punkte, an denen die Einheit normalerweise mit den Hindernissen kollidieren würde, durch 4 grüne Markierungen hervorgehoben)

Da wir für so etwas kein Pathfinding bräuchten, wurden uns von der Requisite ein paar Berge zur Verfügung gestellt, die auch prompt in der Gegend platziert wurden.

Wir haben also nun die Ecken der Hindernisse (Felder: schwarz; Hindernisse: rot; Ecken: blau):

Dadurch können wir uns leicht die Kanten der Hindernisse berechnen:

Es liegt nahe, das Gebiet, in dem nach den Eckpunkten der Hindernisse gesucht wird, so einzuschränken, wie man auf dem nebenstehenden Bild sehen kann. Doch mal angenommen, in diesem Gebiet existiert ein Hindernis, welches nicht vollständig in dieses Gebiet passt. Dann nämlich liegen dessen Ecken außerhalb des Gebietes und die Einheit würde geradewegs in einen Berg laufen, weil sie meint, dass kein Hindernis da ist. 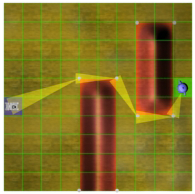Beschäftigen wir uns nun mit der Ermittlung der Punkte, die in der Abbildung hellgrün markiert sind. Dazu prüfen wir zuerst, ob zwischen Start- und Zielpunkt ein Hindernis liegt. Dies wird festgestellt, indem man alle Hinderniskanten auf einen Schnittpunkt mit der Strecke Anfangspunkt-Zielpunkt prüft. Wenn sich keine Strecken schneiden, ist ein direkter Weg möglich. Ansonsten liegt ein Hindernis dazwischen.

Mittels ein wenig Mathematik dürfte die Berechnung des Schnittpunktes zweier Geraden nicht sehr schwer fallen. Interessant wird es jedoch deswegen, weil wir keine Geraden brauchen, sondern mit Strecken arbeiten müssen. Zur Erinnerung: Geraden haben die, in diesem Fall unangenehme, Eigenschaft, dass sie nicht aufhören. Etwas Besserung verschaffen hier Halbgeraden, wirkliche Linderung verspricht aber nur die Strecke, die glücklicherweise einen Anfangspunkt und einen Endpunkt hat. Mithilfe der allgemeinen Geradengleichung sollte man in der Lage sein, eine Funktion aufzustellen, die einem zurückliefert, ob und wo zwei Strecken sich schneiden. Für alle die, wie ich, ein paar Probleme dabei hatten, sei dieses Stückchen Code ans Herz gelegt, das hauptsächlich durch die Beiträge von Lars im Forum entstanden ist:

function LineIntersects(LineA, LineB: TLine): boolean;
  var
    p1, p2,
    q1, q2: TDot;
    a1, b1, c1,
    a2, b2, c2: Single;
    s: TDot;
  begin
    p1.X := LineA.A.X; p2.X := LineA.B.X;
    q1.X := LineB.A.X; q2.X := LineB.B.X;
    p1.Y := LineA.A.Y; p2.Y := LineA.B.Y;
    q1.Y := LineB.A.Y; q2.Y := LineB.B.Y;

    a1 := p2.y - p1.y; b1 := p1.x - p2.x; c1 := a1*p1.x + b1*p1.y;
    a2 := q2.y - q1.y; b2 := q1.x - q2.x; c2 := a2*q1.x + b2*q1.y;

    s.x := (c1*b2-c2*b1)/(a1*b2-a2*b1); s.y := (a1*c2-a2*c1)/(a1*b2-a2*b1);

    Schnittpunkt.X := S.X;
    Schnittpunkt.Y := S.Y;

    Result := True;

    if (s.y > p1.y) and (s.y > p2.y) then Result := False;
    if (s.y > q1.y) and (s.y > q2.y) then Result := False;
    if (s.y < p1.y) and (s.y < p2.y) then Result := False;
    if (s.y < q1.y) and (s.y < q2.y) then Result := False;
    if (s.x > p1.x) and (s.x > p2.x) then Result := False;
    if (s.x > q1.x) and (s.x > q2.x) then Result := False;
    if (s.x < p1.x) and (s.x < p2.x) then Result := False;
    if (s.x < q1.x) and (s.x < q2.x) then Result := False;
  end;

Um den weiteren Ablauf zu erläutern, nehmen wir eine einfachere Karte zur Hand:

Wenn wir nun das Navigationsnetzwerk bauen, schaut das mit etwas Glück so aus:

Was sollen diese roten Nodes (Node = Eckpunkt) in dem Baum? Nun, ganz einfach: Wenn eine rote Node erreicht wird, wird der Baum an dieser Stelle nicht weiter abgegangen. Wären dies nicht so, würde sich eine wunderbare Endlosschleife ergeben, gegen die selbst ein schwarzes Loch alt aus sähe ;). Um herauszufinden, ob eine Node bereits besucht wurde, speichert man die besuchten Nodes in ein Array und schaut jedes Mal im Array nach, ob die aktuelle Node darin enthalten ist. Wenn dem so ist, braucht diese Node nicht abgeganen zu werden, da wir hier schon einmal waren.

Als mögliche Pfade aus dem obigen Netzwerk ergeben sich:

• Start, 1, 2, 3, Ziel
• Start, 1, 3, Ziel
• Start, 2, 1, 3, Ziel
• Start, 2, 3, Ziel
• Start, 3, Ziel

Nun, im Prinzip war das auch schon das ganze Pathfinding. Aber auch nur prinzipiell... Denn gerade die Baumstruktur des Navigations-Netzwerkes schreit geradezu nach einer radikalen Optimierung. Und es gibt wahrlich noch genug Platz, wo man solche Optimierungen einbringen kann ;).

Ausblicke

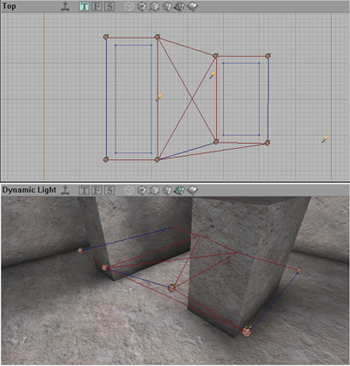
Hier mal zur Abwechslung ein Screenshot vom Unreal Editor. Die Unreal-Engine verwendet ebenfalls Navigationsnetzwerke, damit die Bots ihren Weg finden. Die Äpfel stellen die PathNodes dar. In der Top-Ansicht sieht man, dass ein Pfad fehlt. Das ist aber ein Unreal-spezifisches Problem und hat mit unserem Pathfinding wenig gemeinsam.

Abschluss

Das hier ist mein erstes Tutorial, wo relativ viel Theorie vermittelt wird (werden soll ;) ). Es dauert ein bisschen, bis man bei Pathfinding brauchbare Ergebnisse hat, aber dann hat man ein solides System, welches einem durch alle Schwierigkeiten hindurch den Weg weisen wird ;).

Danken möchte ich an dieser Stelle dem Core-Team von DGL und ganz besonders Phobeus, der mich beim Schreiben immer wieder mit diversen Erheiterungen erheitert hat.

Gruß, Philipp